基于价值修正的圆片下料顺序启发式算法

胡 钢， 杨 瑞， 潘立武

(1. 四川信息职业技术学院信息工程系，四川 广元 628017；2. 郑州科技学院电气工程学院，河南 郑州 450064；3. 河南牧业经济学院自动化与控制系，河南 郑州 450011)

基于价值修正的圆片下料顺序启发式算法

胡 钢1， 杨 瑞2， 潘立武3

(1. 四川信息职业技术学院信息工程系，四川 广元 628017；2. 郑州科技学院电气工程学院，河南 郑州 450064；3. 河南牧业经济学院自动化与控制系，河南 郑州 450011)

讨论圆片剪冲下料方案的设计问题。下料方案由一组排样方式组成。首先构造一种生成圆片条带最优四块排样方式的背包算法，然后采用基于价值修正的顺序启发式算法迭代调用上述背包算法，每次都根据生产成本最小的原则改善目标函数并修正各种圆片的当前价值，按照当前价值生成一个新的排样方式，最后选择最优的一组排样方式组成下料方案。采用文献中的基准测题将文中下料算法与文献中T型下料算法和启发式下料算法分别进行比较。实验计算结果表明，该算法的材料利用率比T型下料算法和启发式下料算法分别高0.83%和3.63%，且计算时间在实际应用中合理。

圆片；剪冲下料；四块排样方式；背包算法；启发式算法

圆片剪冲下料问题是指采用剪切和冲压工艺将库存板材切割出一定数量的若干种圆片毛坯，满足每种毛坯的需求量，使得所使用的板材张数最少。该问题是具有很高计算复杂度的NP难度问题，在机械、家具、船舶等制造行业中有着广泛的存在[1]。目前国内外对矩形下料问题研究较多[2-6]，然而对圆片下料问题研究却比较少，Cui[7]提出了基于 T型排样方式的线性规划下料算法，由于线性规划算法求得的解不一定是整数，最终解需要向上取整，因此解的质量并不高。侯桂玉等[8]提出了基于直切排样方式的启发式下料算法，克服了线性规划算法最终解需要向上取整的缺点，但由于直切排样方式板材利用率比较低下，因此导致最终的排样方案材料利用率并不理想。陈菲等[9]提出了材料利用率较高的三块排样方式生成算法，但是只能解决单张板材上的无约束排样问题，无法解决下料问题。

本文提出基于四块排样方式的顺序价值修正启发式下料算法，用以解决圆片剪冲下料问题，即：①构造一种背包算法生成圆片最优四块排样方式；②采用基于价值修正的顺序启发式算法迭代调用上述背包算法求解下料方案。用该算法求解文献中的例题，更能节省板材消耗。

1 数学模型和相关概念

1.1 问题描述及其数学模型

讨论的圆片剪冲下料(circle cutting stock，CCS)问题可描述如下：已知板材尺寸L×W；有m种圆片，第i种圆片的直径为di，需求量为bi( i= 1,2,···,m )。确定排样方案，用尽量少的板材排出所需的全部圆片。排样方案包含多个不同的排样方式。排样方式是指单张板材上圆片的排列方式[8]。

令J为排样方案包含的排样方式个数，pj= {a1j,a2j, ···,amj}为第j( j= 1,2,···,J )个排样方式中所含圆片情况，其中aij为排样方式中含第 i种圆片的数量。令Z为排样方案使用板材的张数；xj为排样方案包含第j个排样方式的个数；N为非负整数集合。则CCS问题的数学模型为：

其含义是在满足 2个约束条件下最小化板材使用张数。约束条件为：①每种圆片的需求量得到满足；②每种排样方式使用的数量为非负整数。

与 CCS问题紧密相关的是圆片排样(circle cutting packing，CCP)问题，其数学模型为：

其中，V为排样方式的价值，yi为排样方式中包含的第i种圆片的个数，vi为第i种圆片的价值。

1.2 四块排样方式相关概念

1.2.1 条带

如图1所示，条带中可排放一排圆片或多排圆片，其中w为工艺余量。假设w=0，此假设不影响算法的通用性，因为当 w≠ 0时，可令(d+w)为圆片直径。为了满足冲压工艺约束，条带中最多允许排放的圆片排数不超过3[7]。故按照条带所包含圆片的排数可把条带分为3类，定义第i种圆片的 第k类 条 带 其 宽 度 为[10]： t(i-1)×3+ k=，其中， i= 1,···,m ,k= 1,2,3。 m种圆片共有3m种宽度的条带。令 T = [t1,t2,··,t3m]为条带宽度向量。

图1 两种圆片条带

1.2.2 四块排样方式

四块排样方式的详细定义参见文献[11]。图2为一圆片四块排样方式例图，按顺序使用 3条剪切线(图中箭头所示)将板材划分为4个块。左上角块中包含2、10号水平条带；左下角块中包含2、3、8号竖直条带；右上角块中包含5号水平条带；右下角块中包含2、4号竖直条带。分析四块排样方式的几何性质可知，四块排样方式是 T型和直切排样方式的超集，故四块排样方式的板材利用率不会低于T型和直切排样方式。

图2 四块排样方式例图

2 算法原理

2.1 排样方式生成算法

2.1.1 计算条带的价值

令n(j,x)为条带x×tj(长为x，宽为tj)中所含圆片的个数， u(j,x)为条带的价值，其中x≤L，j= 1,···,3 m ，则有[10]：

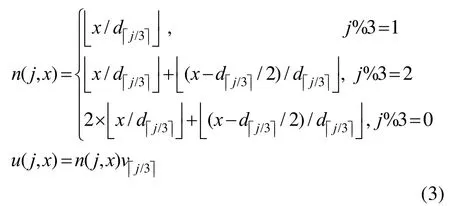
求解式(3)，算法时间复杂度为 O(m L)。

2.1.2 计算块的价值

对于块x×y，不妨设块中条带的长度方向与块的x边方向相同。记 F(x,y)为块的价值，x≤L，y≤W。令 g(j,x)为块中包含条带x×tj的个数，则有：

式(4)是无界背包问题，具体算法可参见文献[12]，时间复杂度为 O(m LW )。

2.1.3 计算四块方式的价值

设四块方式的3条剪切线位置分别为 x,y1,y2，其中 x,y1,y2均为整数。V为四块方式价值，则有：

求解式(5)算法时间复杂度为 O(L W )。

2.1.4 算法步骤

步骤1. 根据式(3)生成所有可能的条带。

步骤2. 根据式(4)生成所有可能的块。

步骤3. 根据式(5)确定最优四块排样方式。

2.2 排样方案生成算法

传统的启发式下料算法生成排样方案可简单描述如下[8]：

(1) 初始化各种圆片的剩余需求量为圆片的需求量。

(2) 使用剩余圆片生成当前排样方式，在尽量少产生多余圆片的前提下，使得该种排样方式尽量重复利用，记录该排样方式以及方式使用次数。

(3) 修改圆片的剩余量，判断有无剩余圆片，若有则转(2)，否则结束循环。

该算法存在贪婪性：好的排样方式(板材利用率较高)在前面出现，而后面的排样方式板材利用率偏低。出现这种情况的原因是：排样方案中各种排样方式顺序产生，先生成的排样方式优先使用容易结合生成好的排样方式的圆片(面积较小的圆片)；而不易结合生成板材利用率高的排样方式的圆片(面积较大的圆片)被用来生成后面的排样方式。该贪婪性使算法容易陷入局部最优，而非全局最优。为了克服该贪婪性，本文算法迭代构造多个排样方案，从中选择板材使用张数最小的作为最终解；在生成每个排样方式后均按照式(6)修正圆片的价值[13-17]。

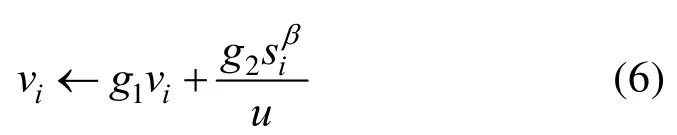
表1列出了本文算法需要用到的变量符号。

表1 变量符号

具体步骤如下：

步骤1. 令 G=1，PNum=∞。初始化圆片价值，若 di≥ 0.5W，则令vi= λsi；否则令vi=si。

步骤2. 按如下步骤产生排样方案：

(1) 令 j= 1，P=Φ，ri=bi(i∈I)。

(2) 调用2.1节排样方式生成算法生成一个排样方式P。

(3) 令 f =m in{ri/ yi|yi＞ 0,i ∈ I }，将P添加到排样方案中。令 ri= ri- fyi,i∈ I ，修改圆片的剩余量。

(4) 按照式(6)修正圆片的当前价值；如果存在ri＞ 0(i ∈I )，则令 j=j+ 1并转(2)。

步骤 3. 如果排样方案使用的板材张数小于PNum，则保存排样方案，并记PNum为排样方案使用的板材张数。

步骤4. 令 G=G+1，如果 G＞Gmax，输出排样方案，否则转步骤2。

2.3 下料算法时间复杂度

本文算法总共构造了Gmax个排样方案；每个排样方案考察了个排样方式。由于四块排样方式生成算法时间复杂度为 O(m LW )，因此该算法总的时间复杂度为 O(mLWMGmax)。

3 数值实验

用C#语言在主频为2.7 GHz、内存为2 GB的计算机上进行实验。参数 α= 0.75，β=1.03，Gmax= 200。采用文献中的测题，将本文算法和文献中的下料算法进行比较。

3.1 与文献[7]下料算法比较

采用文献[7]的20道测题，板材长为2 000，宽为1 000，剪冲工艺余量为8，每条条带最多允许排放3排圆片，圆片直径在区间[100, 500]均匀分布，圆片需求量在区间[500, 3000]均匀分布。具体数据及文献[7]算法下料利用率统计结果，参见排样网站 http://www.gxnu.edu.cn/Personal/ydcui/ English/Problems/COR2005-32-01.DTXT。

20道测题，本文算法平均下料利用率为72.56%，文献[7]算法平均下料利用率为71.73%，可见本文算法平均下料利用率比文献[7]算法高0.83%。求解20道测题文中算法总共耗时12.69 s，平均每道测题耗时 0.63 s；文献[7]算法总共耗时12.92 s，平均每道测题耗时0.65 s，本文算法和文献[7]算法计算时间近似，能满足实际应用需要。

图 3为本文算法求得的测题 18的排样方案图，包含10个排样方式，其中图3(a)表示按照排样方式1切割59张板材；排样方案总共使用716张板材，板材利用率为73.06%；文献[7]算法排样方案总共使用724张板材，板材利用率为72.26%。

图3 测题18的排样方案

3.2 与文献[8]下料算法比较

采用文献[8]的15道随机测题来检验本文算法。测题具体数据见文献[8]第4节。对于15道测题，本文算法求得的排样方案板材平均利用率为72.85%，文献[8]算法求得的排样方案板材平均利用率为69.22%。图4为本文算法求得的测题1的排样方案图，共使用板材 77张，板材利用率为77.79%；文献[8]算法求得的测题1的排样方案共使用板材84张，板材利用率为71.27%，可见本文算法能够显著的提高材料利用率。

图4 测题1的排样方案

3.3 一个生产实例的求解

某电机制造厂用规格为3000 mm×1500 mm的硅钢板材，切割出8种尺寸不同的圆片，表2所示为圆片具体规格和需求量，剪冲工艺余量为6 mm。采用传统启发式算法下料利用率为69.62%，采用本文价值修正的顺序启发式算法下料利用率为 74.16%，明显的提升下料利用率，减少余料浪费。

表2 圆片直径和需求量

4 结 论

实现了基于四块排样方式的圆形片剪冲下料算法，在生成排样方案的过程中通过不断修正各圆片价值，使得排样方式更加趋于合理。实验结果表明，本文算法材料利用率比文献[7]和[8]算法分别高0.83%和3.63%。将本文的四块排样方式生成算法和整数规划相结合，设计剪冲下料问题的精确算法可以作为以后研究的方向。

[1] Wäscher G, Haußner H, Schumann H. An improved typology of cutting and packing problems [J]. European Journal of Operational Research, 2007, 183(3): 1109-1130.

[2] 潘卫平, 陈秋莲, 崔耀东, 等. 基于匀质条带的矩形件最优三块布局算法[J]. 图学学报, 2015, 36(1): 7-11.

[3] Dusberger F, Raidl G R. Solving the 3-staged 2-di mensional cutting stock problem by dynam ic programming and variable neighborhood search [J]. Electronic Notes in Discrete Mathematics, 2015, 47: 133-140.

[4] Kim K, Kim B I, Cho H. Multiple-choice knapsack-based heuristic algorithm for the two-stage two-dimensional cutting stock problem in the paper industry [J]. International Journal of Production Research, 2014, 52(19): 5675-5689.

[5] Gómez J C, Terashima-Marín H. Building general hyper-heuristics for multi-objective cutting stock problems [J]. Computacióny Sistemas, 2012, 16(3): 321-334.

[6] A ryanezhad M B, Hashem i N F, Makui A, et al. A simple approach to the two-dimensional guillotine cutting stock problem [J]. Journal of Industrial Engineering International, 2012, 8(1): 1-10.

[7] Cui Y D. Generating optimal T-shape cutting patterns for circular blanks [J]. Computers & Operations Research, 2005, 32(1): 143-152.

[8] 侯桂玉, 崔耀东, 黄少丽, 等. 一种求解圆形件下料问题的启发式算法[J]. 计算机工程, 2010, 36(13): 227-229.

[9] 陈 菲, 刘 勇, 刘 睿, 等. 基于3块方式的圆形片剪冲排样算法[J]. 计算机工程, 2009, 35(14): 195-196.

[10] Cui Y D, Gu T L, Hu W. A cutting-and-inventory control problem in the manufacturing industry of stainless steel wares [J]. Omega, 2009, 37(4): 864-875.

[11] 易向阳, 仝青山, 潘卫平. 矩形件二维下料问题的一种求解方法[J]. 锻压技术, 2015, 40(6): 150-154.

[12] Kellerer H, Pferschy U, Pisinger D. Knapsack problems [M]. Berlin: Springer, 2004: 211-234.

[13] Cui Y D, Cui Y P, Zhao Z G. Pattern-set generation algor ithm for the one-dimensional cutting stock problem with setup cost [J]. European Journal of Operational Research, 2015, 243(2): 540-546.

[14] Cui Y D, Yang L, Zhao Z G, et al. Sequential grouping heuristic for the two-dimensional cutting stock problem with pattern reduction [J]. International Journal of Production Econom ics, 2013, 144(2): 432-439.

[15] Cui Y P, Cui Y D, Tang T B. Sequential heuristic for the two-dimensional bin-packing problem [J]. European Journal of Operational Research, 2015, 240(1): 43-53.

[16] Cui Y P, Tang T B. Parallelized sequential value correction procedure for the one-dimensional cutting stock problem with multiple stock lengths [J]. Engineering Optim ization, 2014, 46(10): 1352-1368.

[17] 姚 怡, 赖朝安. 一种带剪切约束的启发式二维装箱算法[J]. 图学学报, 2015, 36(6): 879-886.

Sequential Value Correction Heuristic Algorithm for the Circle Cutting Stock Problem

Hu Gang1, Yang Rui2, Pan Liwu3

(1. Information Engineering Department, Sichuan Institute of Information Technology, Guangyuan Sichuan 628017, China; 2. School of Electrical Engineering, Zhengzhou University of Science＆Technology, Zhengzhou Henan 450064, China; 3. Department of Automation and Control, Henan University of Animal Husbandry & Economy, Zhengzhou Henan 450011, China )

This paper discusses the problem of generating optimal cutting plan for circles. The cutting plan consists of several cutting patterns. First a knapsack algorithm that generating four-block cutting patterns of circle strips was constructed; then the sequential value correction heuristic algorithm was used to generate the cutting plan, it iteratively calls the above knapsack algorithm procedure improves the objective function based on the principle of m inimum production cost and correct the current value of circles, generates a new pattern according to the current value; in the end a set of optimal cutting patterns was choose to form the cutting plan. The cutting stock algorithm was tested with the benchmark problems of literatures, and compared with the T-shape algorithm and heuristic algorithm. The results of numerical experiments show that, the material utilization rate of the algorithm is higher 0.83% and 3.63% than the above two algorithms.

wafer; cutting stock; four block patterns; knapsack problem; heuristic algorithm

TP 391

10.11996/JG.j.2095-302X.2016030337

A

2095-302X(2016)03-0337-05

2015-11-03；定稿日期：2015-11-25

河南省科技厅科技攻关项目(152102210320)；河南省高等学校重点科研项目(15B52000)

胡 钢(1982–)，男，四川泸州，讲师，本科。主要研究方向为优化计算、软件开发、实验室管理。E-mail：rtfdgl@163.com

潘立武(1971–)，男，河南杞县人，副教授，博士。主要研究方向为智能计算、CAD、软件开发。E-mail：hge5963@163.com