时域积分在振动信号分析中的应用

许自顺， 张强

(山东大学能源与动力工程学院， 山东 济南 250061)



·测试与诊断·

时域积分在振动信号分析中的应用

许自顺， 张强

(山东大学能源与动力工程学院， 山东 济南 250061)

为研究某装载机样机配置的新型发动机罩的振动特性，利用三维建模建立装载机发动机罩模型并使用有限元法对其进行了模态分析，重点分析了前几个阶次的固有频率和振型，结果显示发动机罩整体存在刚度偏低以及低阶次模态振型分布集中的现象。对样机发动机罩的水平和垂直两个敏感方向进行了振动加速度测量，对比了两种信号积分方法的使用范围及优势，利用时域积分方法对所测加速度信号进行了积分处理，并用最小二乘法拟合积分信号中的趋势项加以修正，得到了较为精确的振动速度及位移信号。通过对机罩两个敏感方向的振动加速度、速度和位移信号的综合分析，判断发动机罩刚度偏低，振动量偏大，易产生干涉。模态分析及振动信号分析结果为下一步发动机罩样品的优化改进提供理论依据及改进方向。

模态分析； 振动信号； 时域积分； 拟合； 趋势项

随着数值计算方法的发展,有限元技术(FEM)越来越多地被应用到机械部件的初期设计,将结构体的复杂振动分解为多个简单而独立的模态，并用一系列的模态参数如固有频率和振型来表征[1]，已经逐渐成为主要的辅助手段。在初期产品的设计时，可以通过建立有限元计算模型对结构的振动特性进行分析，并对产品样品进行初步的试验，结合样品的试验数据进行综合评价以发现产品设计中的不足。模态分析和实测相关数据可以为进一步的产品优化升级提供理论依据和改进方向[2-3]。

在研究结构的动态特性时,通常需要应用结构的动态位移、速度或加速度响应信号。振动加速度反映振动的冲击力度，振动速度又叫振动烈度，反映振动能量的大小，振动位移直接反映振动体的位置变化量，理论上3种响应信号之间存在着微分和积分的关系[4]。工程应用中，加速度信号因其传感器体积小、精度高而被选择为分析应用中的直接测量信号。可通过积分运算来求取其他两种信号，目前常用的积分方法有时域积分和频域积分。时域积分对测得的加速度信号直接进行积分，会出现趋势项干扰，需要拟合多项式趋势项以去除信号偏移；频域积分先对原始信号作傅里叶变换转化为频域信号，再对频域信号进行积分运算[5-6]，由于动态信号对于下限截止频率非常敏感，当低频截止频率选取在较低值时,传统二阶频域积分可产生较大的动位移低频振荡和峰值误差[7-8]。综合两种方法的应用范围及精度，实际应用时，在处理一般中高频的信号时常采用频域积分，而遇到诸如工程机械类发动机机罩低频晃动问题分析时，采用时域积分更为准确有效。

1 发动机罩模态分析

发动机罩的振动是其各阶次模态的综合反映[9]，研究对象为某装载机新型一体式机罩(见图1)，为了更好地了解发动机罩的模态属性，以便于为之后的设计和改进提供参考，用三维建模方法建立发动机罩的几何模型，并用有限元法对其进行了模态分析。具体实施步骤如下：

1) 建立发动机罩三维模型，只取主体结构，保留顶面开孔和风窗，除去两侧窗体；

2) 抽取机罩的中面建立壳体单元，壳体骨架之间用模拟焊接单元建立刚性连接，在发动机罩的4个固定螺栓位置建立前后、左右和上下3个方向的约束，使其不能在该3个方向上移动；

3) 赋予壳体单元不同位置以实际的厚度和材料属性等，材料弹性模量为2.06×105MPa，泊松比为0.3，密度为7.8 g/cm3；

4) 选择计算参数进行前八阶模态有限元计算，利用后处理软件显示各阶次模态频率及振型云图。

表1示出了有限元计算得出的发动机罩前八阶模态频率及振型。

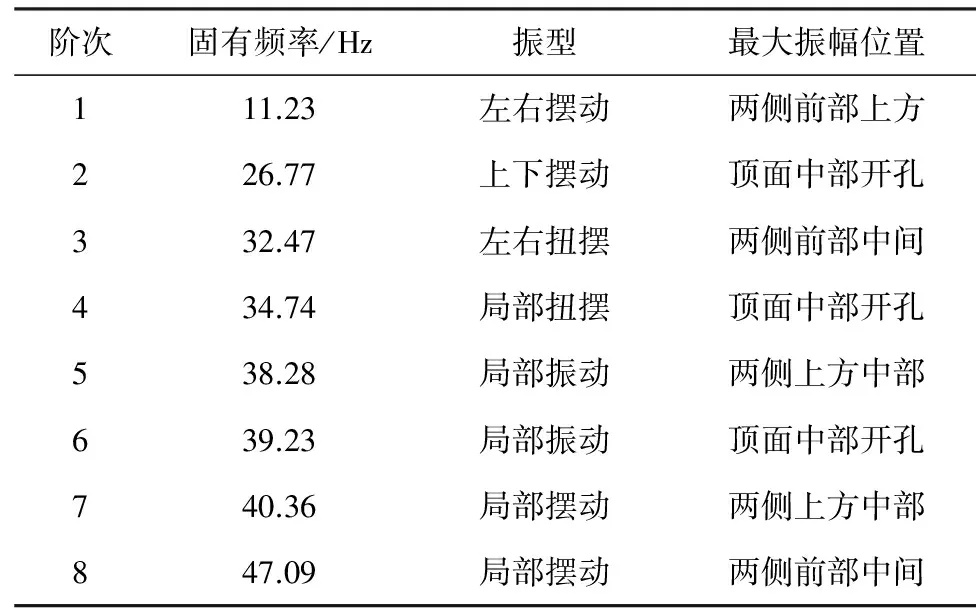
表1 前八阶模态频率及振型

因研究的目的主要是为解决机罩的低频晃动问题，并且共振时振动能量主要分布在低阶次模态，因此只选取计算的前四阶模态进行分析[10-11]。

根据模态分析的结果，在约束状态下，当以第一阶模态振动时，振型云图显示机罩整体将会产生左右方向的摆动(见图1a)，由于对机罩底部进行了约束，摆动偏移量以机罩上部前半部分最大，机罩整体左右方向上的摆动也说明了发动机结构在该方向上的刚度较低；当机罩以第二阶模态振动时会产生上下方向的变形运动(见图1b)，最大变形量在上部盖板中部开孔处，其次为侧面上部；第三阶模态振型为机罩前部和后部在左右方向的交替摆动，使机罩整体出现扭曲，最大位移在机罩前部中间位置(见图1c)；第四阶模态振型则为局部振动，范围较小，位移主要在机罩顶板的开孔处(见图1d)。

前三阶振型中发动机罩较大范围都存在相对较大的变形，尤其第一阶固有频率偏低，会使得整体在左右方向上发生较大晃动；机罩尾部侧面、盖板和后围板之间相互焊接固定，增加了刚度，机罩前部处于悬空状态，为整体刚度最低处；上盖板跨度大、开孔较多，降低了其垂向刚度。另外前四阶振型主要为上下和左右方向的变形，所以其低阶次的模态分布不合理，应该尽量使振型分配分散，从而降低振动能量在某个方向的集中分布[12]。综合前四阶的模态特性，刚度不足尤其左右方向上刚度偏低以及低阶模态分布的不合理导致该机罩在一定的激励下容易产生较大的振动变形[13]，并且以左右方向最为显著。

2 试验装置与信号采集

试验在某工程机械实验室进行，试验样机为装置一体式发动机罩的装载机，装载机样机后部发动机罩通过4个螺栓和车架相连，发动机罩上方无固定装置。为了研究由于摆动产生的不均匀性冲击激励对一体式发动机罩振动的影响，需要得到其时域内的相关振动信息[14]。利用3560c Pulse数据采集系统采集并记录时域振动加速度信号。加速度传感器放置在机罩顶面和侧面(见图2)，同时采集垂向和左右方向的振动加速度。装载机不行走，只在原地模拟转向动作，在采集信号时驾驶员操纵方向盘使装载机连续左右摆动以便能够捕捉到转向极限位置的振动信号。图3示出一个摆动循环的实测加速度时域信号。

从实测的振动加速度看出，在装载机转向过程中发动机罩振动加速度信号呈现比较明显的不规律性，振荡极限值随时间不断变化，尤其在该次信号开始采集后的1.3 s附近振幅突然增大，之后振荡减小。可判断该对应时刻装载机转向达到极限位置开始反向摆动，整个过程中左右方向的振动烈度明显大于上下方向，水平振动加速度约为上下方向的2倍，说明转向过程中车架给予发动机罩水平方向的冲击较为严重。由于振动信号在时域上的正负交替性变换，其幅值并不能直接反映在对应方向上的速度和位移的幅度。因此，要综合评价机罩在水平和垂直方向上的振动特性，还需要得到其对应的振动速度和位移信号。

3 信号处理及分析

3.1 时域积分基本理论

在实际测量中，由加速度传感器所测得的加速度信号会不可避免地带有噪声干扰和测量误差偏移，即使一些配套采集设备已具备屏蔽干扰的硬件及软件措施，测量中由设备及各种环境因素造成的测量误差依然存在，造成加速度信号的零点a0偏移[15]。

设初始速度和初始位移分别为v0，s0，加速度传感器所测得的加速度信号为a(t)，则真实的加速度应为a(t)-a0，按照理论计算的速度和位移分别为

v(t)=v0-a0t+∫a(t)dt，

(1)

(2)

式中：t为时间；v(t)，s(t)分别为t时刻对应的速度和位移。

v0，s0和a0为未知项，在实际的积分计算中不考虑这些项从而得到：

v(t)=∫a(t)dt，

(3)

s(t)=∫v(t)dt=∫∫a(t)dtdt。

(4)

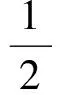
3.2 趋势项的消除

要减小信号中存在的趋势项对分析信号的影响，就要把速度信号中的一次趋势项和位移信号中的二次趋势项除去，常用消除趋势项的方法为多项式的最小二乘法[19]。

设需要去除的趋势项的振动离散信号为{xi}，(i=0,1,2…n-1)，采样周期为Δt，利用m次多项式函数

(5)

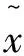
(6)

通过求解离散加速度信号对应的最小二乘法的法方程组，可以求得各待定系数进而求出趋势项。速度信号存在一次趋势项，可取m=1；位移信号存在二次趋势项，取m=2。将直接积分得到的速度和位移信号减去对应的趋势项函数即可得到更为精确的分析信号[20]。

3.3 信号时域积分处理及分析

以初始速度、位移为0，对加速度信号积分处理时采用梯形积分公式：

(7)

(8)

式中：i=0,1,2…n-1；vi和si分别为第i个采样点的速度值和位移值。

分别对采集的左右方向和上下方向的振动加速度信号进行一次积分，可得到带有趋势项的振动速度信号(见图4)；再对速度信号进行一次积分，可得到带有趋势项的振动位移信号[21](见图5)。

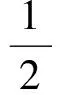
拟合曲线如图4、图5中虚线，对比信号曲线和拟合曲线可知，拟合曲线能够很好地反映出积分所得信号偏差趋势，将此偏差趋势从积分所得信号中除去，即可得到较为精确的所需分析信号[22]。最终去除趋势项之后的振动速度和位移曲线见图6。

图6a所示的振动速度曲线体现了整个装载机模拟转向的过程中发动机罩的振动速度变化。对比可知，在左右方向的振动速度明显高于上下方向：在单一方向的摆动过程中，左右振动速度约为上下振动速度的2倍；在换向(约1.3 s位置)时，由于车架给发动机罩的冲击主要为左右方向，该方向的振动速度急剧增加，峰值达到0.2 m/s以上，在之后衰减的过程中水平振动加速度也远大于垂向。因此判断转向过程中发动机罩的振动能量主要在水平方向。修正后的振动位移曲线见图6b，相对于振动速度，振动位移峰值的变化不是特别剧烈，整个过程呈现低频率的过渡变化过程。最大振动位移仍然出现在换向时段，相对于平衡位置的最大水平位移为7 mm，最大垂向位移为4 mm。可以判断转向时振动位移较大，在装载机工作或道路环境恶劣的条件下将会产生更大的振动位移，可能造成发动机罩与内部或外部构件的位置干涉，从而造成结构损伤。

通过对振动加速度、速度和位移动态信号的分析，判断发动机罩水平方向刚度偏低。机罩底部有4个螺栓进行固定约束并焊接加强筋，两侧面只有4根垂向的加强筋进行加固，因此机罩上部近似于悬空，下部有冲击时，上部在左右方向上就很容易产生较大的位置偏移。另外机罩顶部加强筋相距较远，盖板跨度大中间位置也容易引起上下振颤。

4 结论

a) 对发动机罩进行了三维建模，并使用有限元法对机罩进行了模态分析，得到其固有频率及振型；分析结果表明，发动机罩整体刚度较小以及低阶次模态振型分布的集中性使得机罩在水平和垂直两个方向易发生振动变形，其中以机罩前段中部和上部最为明显；

b) 对实测发动机罩加速度信号进行时域积分得到水平和垂向的振动速度及振动位移信号，并使用最小二乘法去除了积分所得信号的趋势项，拟合结果很好地反映了振动信号的偏移趋势，最终得到了较为精确的振动速度、位移信号；

c) 利用所测加速度信号及去除趋势项的速度、位移信号对发动机罩进行了振动分析，机罩在水平垂直方向上振动能量较高、振动位移偏大；较高的振动能量和位移会减短机罩的使用寿命，恶劣工况下可能产生部件之间的干涉，造成干涉部件的损坏，从而验证了模态分析的结果。

[1] 蔡力钢,马仕明,赵永胜,等.多约束状态下重载机械式主轴有限元建模及模态析[J]. 机械工程学报，2012,48(3):88-94.

[2] Akash Shukla,Harsha S P.An experimental and FEM modal analysis of cracked and normal steam turbine blade[J].Materials Today: Proceedings,2015,2(4/5):2056-2063.

[3] 陈志勇,史文库,沈志宏,等. 轻型客车车身车架整体结构有限元模态分析[J].振动与冲击，2010(10):244-246,263.

[4] 顾名坤，吕振华．基于振动加速度测量的振动速度和位移信号识别方法探讨[J].机械科学与技术，2011，30(4):522-526．

[5] 朱文发,柴晓冬,郑树彬,等.基于积分滤波器的位移信息获取[J].仪表技术与传感器，2012(5):62-64.

[6] 董礼,廖明夫,杨伸记.振动信号频域积分的滤波修正算法[J].机械设计与制造,2010,1(1):46-48.

[7] 王继新，季景方，张英爽，等． 基于小波分形理论的工程车辆时域载荷信号降噪方法[J].吉林大学学报(工学版),2011,41(增2):221-225.

[8] 李强,王太勇,胥永刚.基于频域积分的振动参量转换修正算法[J].组合机床与自动化加工技术,2005(9):60-61,65.

[9] 袁海峰.叶轮叶片振动模态分析与实验研究[D].武汉:武汉理工大学,2010.

[10] 李小彭，赵志杰，聂慧凡，等． 某型数控车床床身的模态分析与结构优化[J]． 东北大学学报(自然科学版)，2011，32(7): 988-991．

[11] 赵万华，杜超，张俊，等. 主轴转子系统动力学解析建模方法[J].机械工程学报，2013，49(6)：44-51.

[12] 司景萍，韩璐，任庆霜，等. 基于 ANSYS 的自卸车副车架结构模态分析[J].内蒙古工业大学学报，2011(3)：329-333.

[13] 郭荣,周鋐. 某型轿车白车身试验模态分析及动态特性评价[J].机械设计，2010，27(8)：18-22.

[14] 陈为真，汪秉文，胡晓娅．基于时域积分的加速度信号处理[J]．华中科技大学学报(自然科学版)，2010,38(1):1-4．

[15] Hong Y H，Kim H K，Lee H S.Reconstruction of dynamic dis-placement and velocity from measured accelerations using the vibrational statement of an inverse problem[J]．Journal of Sound and Vibration,2010(329):4980-5003．

[16] WANG J X,TANG X B. Wavelet denoise method applied in load spectrum analysis of engineering vehicles[J]． Advanced Materials Research，2010,108:1320-1325．

[17] 张义民,宿苏英,李鹤,等. 随机连续梁弯曲振动系统的频率可靠性分析[J].应用力学学报,2007,24(1)：133-136.

[18] 王得志.非高斯振动环境下的装备结构可靠性研究[D].长沙:国防科技大学,2010.

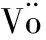
[20] Lyudmila Sakhanenko. Rate acceleration for estimators of integral curves from diffusion tensor imaging (DTI) data[J].Statistics & Probability Letters,2015,107(12):286-295.

[21] ZHOU Yucai, CHEN Shian, WANG Juncheng. Two-acceleration-error-input proportional-integral-derivative control for vehicle active suspension[J].Journal of Traffic and Transportation Engineering(English Edition),2014,1(3):228-234.

[22] 王济,胡晓.MATLAB在振动信号处理中的应用[M].北京:中国水利水电出版社,知识产权出版社,2006：104-107.

[编辑： 潘丽丽]

Application of Time Domain Integral Method in Vibration Analysis

XU Zishun, ZHANG Qiang

(School of Energy and Power Engineering， Shandong University， Ji’nan 250061， China)

To study the vibration characteristics of the new engine hood for a prototype loader, the hood model was built by three-dimensional modeling and the modal analysis was conducted with the finite element method (FEM). The natural frequencies and vibration modes of first few orders were especially analyzed, and the results showed that the stiffness of the whole hood was inadequate and the low order vibration modes concentrated. The hood vibration accelerations in the horizontal and vertical direction were measured and the using range and advantage of integral method for two signals were compared. The integral processing of measured acceleration signals was conducted with the time domain integral method, the trend item of integral signal was corrected with the least square method, and then the more precise vibration velocity and displacement signal were acquired. Through the comprehensive analysis of hood vibration acceleration, velocity and displacement signal in two sensitive directions, it was found that the stiffness of the hood was inadequate and the vibration magnitude was large enough to cause interference. Modal and signal analysis results provided the theoretical basis and improvement direction for the engine hood optimization.

modal analysis; vibration signal; time domain integral; fitting; trend item

2016-01-04；

2016-03-16

国家科技支撑计划资助项目(2015BAF07B04)

许自顺(1990—)，男，硕士，主要研究方向为动力机械的减振降噪；xuzishun0925@163.com。

张强(1973—)，男，博士，讲师，主要研究方向为气体燃料发动机；sduzq01@163.com。

10.3969/j.issn.1001-2222.2016.04.016

TK401

B

1001-2222(2016)04-0087-06