大跨径曲线连续刚构桥静载试验及承载力研究
2016-11-28王伟靳国胜奉龙成张玉平
王伟, 靳国胜, 奉龙成, 张玉平
(1.重庆中设工程设计股份有限公司, 重庆400025;2.重庆中检工程质量检测有限公司, 重庆400025;3.西南交通大学土木工程学院, 成都610031;4.长沙理工大学土木与建筑学院, 长沙410064)
大跨径曲线连续刚构桥静载试验及承载力研究
王伟1,2,3, 靳国胜2, 奉龙成1, 张玉平4
(1.重庆中设工程设计股份有限公司, 重庆400025;2.重庆中检工程质量检测有限公司, 重庆400025;3.西南交通大学土木工程学院, 成都610031;4.长沙理工大学土木与建筑学院, 长沙410064)
以国家高速公路上一座大跨径曲线连续刚构桥为研究对象,首先建立了桥梁有限元分析模型,并对结构进行了静载试验,获得了桥梁结构在试验荷载下的挠度与应变变化规律,然后运用最小二乘原理并结合试验获得的实测数据,利用模型修正技术对初始理论模型进行了修正,最后在此基础上对结构的实际承载力进行研究。研究表明:该桥处于弹性工作范围内,整体结构性能良好,修正后的模型能够反映当前桥梁的受力状态,结构承载力满足要求。
连续刚构桥;静载试验;模型修正;承载力
引言
大跨径连续刚构桥因具有结构跨越能力大、整体性能好、结构受力合理明确、结构型式简洁明快等优点,备受工程界的青睐,得到了快速发展,自1988年从国外引进后,我国于1990年建成了第一座预应力刚构桥,即主跨为180 m的广州洛溪大桥[1]。在兴建过程中因地质、线形等要求,曲线连续刚构桥被提了出来,曲线桥梁可以很好地适应地形地物对桥址的限制,使整体线形平顺流畅、明快大方[2],然而曲线刚构桥的受力较直线桥要复杂得多,对其成桥后的质量评定就显得尤为重要。
目前大多数文献均是针对常规桥型进行荷载试验分析,很少有关于曲线连续刚构桥荷载试验的研究,而且也仅仅是依据荷载试验层面来评估桥梁的质量状况,略显粗糙[3]。以沈海国家高速公路上一座跨径组合为(60+100+60)m大跨径曲线连续刚构桥为研究对象,首先对其进行了静载试验,获得了控制截面的挠度及应变在试验荷载下的变化规律,然后利用模型修正技术,使得初始有限元模型能够准确真实地反映出桥梁的实际受力状态,最后在此基础上对结构的承载力进行了研究。
1工程概况及模型建立
1.1工程概况
沈海国家高速公路谢边至三堡段上某主桥为跨径组合(60+100+60)m全预应力混凝土变截面连续刚构箱梁,跨越佛开高速,位于R=588 m的圆曲线上(图1)。其箱梁采用C50混凝土,梁体为单箱双室断面,主墩墩身采用C40混凝土,薄壁箱型墩断面,基础由8D200 cm桩组成。沥青混凝土桥面铺装,桥梁宽度20.50 m,双向四车道,设计荷载为公路-I级。

图1主桥桥型布置图(单位:cm)
1.2模型建立
试验为基本荷载试验,根据《大跨径混凝土桥梁的试验方法》[4]的要求,桥梁的静力试验按荷载效率η确定试验的最大荷载。静力荷载效率η的计算公式为:
(1)
式中:Sstat、Sd分别为试验荷载与设计标准荷载作用下结构内力的计算值;(1+μ)为设计取用的冲击系数。
运用三维线性分析方法,严格按照桥梁竣工图纸,采用midas Civil建立结构的空间有限元模型计算结构在设计荷载作用下的内力反应。全桥均用3-D梁单元建模,其中,主梁与主墩身混凝土的弹性模量均按照《JTG D62-2004 公路钢筋混凝土及预应力混凝土桥涵设计规范》进行取值,即C50混凝土为3.45×104MPa,C40混凝土弹性模量为3.25×104MPa;预应力钢绞线用Strand1860模拟,并根据桥梁实际布置情况输入预应力钢束的特征值与形状,以便程序在后续分析中自动计算
预应力效应,同时考虑支座的实际位置,模型共划分247个节点,238个单元,如图2所示。

图2桥梁三维有限元模型
2静载试验分析
2.1试验内容
根据该桥前期普查情况并结合规范[4]要求,静载试验共分为3个工况[5],主桥箱梁控制截面选为距J14墩23 m处A-A截面、墩顶支座附近B-B截面、中跨跨中C-C截面(图1)。具体工况内容、控制内力值及荷载效率η见表1。

表1静载试验各工况的控制截面、内力值与荷载效率η
2.2结果分析
主桥挠度观测点布置在桥面,挠度测点共28个,桥面挠度测点布置如图3所示,应变测试断面选在A-A、B-B、C-C截面底面和侧面布置,各截面均布置15个应变测点,合计共45个测点,其中C-C截面应变测点布置如图4所示,各试验工况下控制截面挠度及应变校验系数及残余系数详见表2。

图3桥面挠度测点布置(单位:cm)
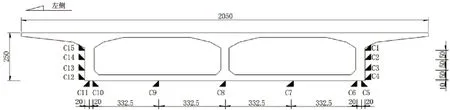
图4C-C截面应变测点布置(单位:cm)
表2中,Stot表示满载时实测总变形(应变)值,Sp表示卸载后实测残余变形(应变)值,Se表示结构实测弹性变形(应变)值,Sstat表示理论计算弹性变形(应变)值,K表示校验系数,ξ表示相对残余,且挠度向下为正,应变拉为正。从表2可知,各工况下控制截面实测挠度、梁底拉应变的校验系数K在0.77~0.85之间,满足文献[4]中0.70≤K=Se/Sstat≤1.05的要求;残余变形系数ξ在0.01~0.18之间,满足文献[4]中ξ=Sp/Stot≤0.20的要求,且试验中测得的试验桥跨满载时控制截面挠度最大实测值分别为6.04 mm(边跨)、14.00 mm(中跨),满足文献[6]中[f]≤l/600=100.00 mm(边跨)、166.67 mm(中跨)的要求,说明结构强度及刚度均满足设计要求,结构处于弹性工作状态,且具有一定的安全储备。

表2挠度及应变校验系数及残余系数
3模型修正及承载力研究
3.1模型修正
Mottershead和Friswell总结了有限元模型误差产生的主要因素及方式,并得出模型的误差主要来自模型的结构误差、模型的参数误差与模型的阶次误差三个方面[7-9]。在静载试验前,首先对箱梁尺寸及混凝土强度进行了量测,并与设计资料比较发现,箱梁尺寸与设计值存在些许偏差,箱梁混凝土强度偏高。为了使初始有限元模型能够准确真实地反映结构当前受力状况,须对模型进行修正[10-12]。
运用最小二乘原理,结合静载试验获得的各工况下挠度值,建立挠度残差最小的修正函数[13-15]:
(2)
式中:f(x)是目标函数,即修正函数;x是设计变量,即待修正参数;gi(x)是状态变量,即约束函数。
造成初始有限元模型与实际结构之间的误差因素有很多,诸如混凝土超方、构件尺寸、结构材质(混凝土弹模与质量密度)、桥面铺装层厚度等,由于混凝土的弹性模量与质量密度对结构的刚度影响较大,故此次主要对这两者进行了修正,修正后混凝土的弹性模量有所提高,这与现场检测结果相一致。由于混凝土中有钢筋,而初始有限元模型中单元材质为素混凝土,故修正后的混凝土质量密度也增大。
模型修正前后工况一和工况三各测点的挠度曲线对比如图5和图6所示。

图5工况一下模型修正前后挠度曲线

图6工况三下模型修正前后挠度曲线
由图5和图6可知,模型修正后理论值与实测值的误差从23%降低到7%,各计算值均与实测值相吻合,说明修正后的模型能够准确真实地反映该桥梁结构的实际受力状态,能够在此基础上进行承载力研究。
3.2承载力研究
静载试验中的校验系数是评定桥梁承载力的重要指标,但是其范围较大,评估较为粗劣。要精确得出承载能力极限状态下结构的承载力,就须在修正后的有限元模型上不断地施加外荷载,并考虑非线性的影响进行分析。当外荷载使得结构切线刚度矩阵趋于奇异时,结构失稳,承载能力就达到了极限,此时的外荷载即为极限荷载[16-18],其实求解结构承载力的过程就是非线性屈曲分析问题。
按照结构最不利受力状态进行布载,限于篇幅,仅列出考虑非线性影响后的J15墩顶荷载-位移曲线,如图7所示。

图7J15墩顶荷载-位移曲线
由图7可知,在A点之前结构处于弹性工作状态,此时A点(488.32×103kN/m)为结构的屈服荷载,从A点到B点结构处于弹塑性工作状态,此时B点(721.26×103kN/m)为结构的极限荷载,即为该桥梁结构的极限承载力,其值远远大于公路-I级(PK=360 kN,qK=10.5 kN/m),说明该桥承载力满足要求,具备通行公路-I级的能力。
4结论
(1)各工况下控制截面的实测挠度、应变数据均小于理论计算值,且校验系数与残余变形系数均满足规范的相关规定,说明结构强度及刚度均满足设计要求,结构处于弹性工作状态,且具有一定的安全储备。
(2)利用静载试验获得的挠度值对初始理论模型进行了修正,修正后的模型各计算值均接近实测值,说明修正后的模型能够准确真实地反映该桥梁结构的实际受力状态,能够在此基础上进行承载力分析。
(3)利用修正后的模型进行非线性屈曲分析得出的极限外荷载即为实际桥梁结构的极限承载力,其值远大于公路-I级荷载,说明该桥承载力满足要求,具备通行公路-I级的能力。
[1] 马保林.高墩大跨连续刚构桥[M].北京:人民交通出版社,2001.
[2] FENG J X,DONG J,LIANG T.Studies on the Mechanical Performance of Long Span Continuous Rigid Frame Bridge under the Influences of Different Curvature Radius[J].Advanced Materials Research,2014,1020:119-123.
[3] 代筠杰,周康静,李力,等.大跨高墩曲线连续刚构桥荷载试验[J].中国市政工程,2010(5):18-20.
[4] 交通部公路科学研究所.大跨径混凝土桥梁的试验方法[M].北京:人民交通出版社,1982.
[5] 湛润水,胡钊芳.公路桥梁荷载试验[M].北京:人民交通出版社,2003.
[6] JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].
[7] FRISWELL M,MOTTERSHEAD J E.Finite element model updating in structural dynamics[M].Germany:Springer,2010.
[8] GUO N,YANG Z,JIA Y,et al.Model updating using correlation analysis of strain frequency response function[J].Mechanical Systems and Signal Processing,2016,70:284-299.
[9] ARRAS M,COPPOTELLI G.Finite-Element Structural Updating Using Frequency Response Functions[J].Journal of Aircraft,2015,52(5):1454-1468.
[10] HONG W,WU Z,YANG C,et al.Finite element model updating of flexural structures based on modal parameters extracted from dynamic distributed macro-strain responses[J].Journal of Intelligent Material Systems and Structures,2015,26(2):201-218.
[11] 何涛,张巍,吴植安.基于动静载试验数据的预应力混凝土梁模型修正方法试验研究[J].公路交通科技,2015,32(12):75-80.
[12] JAYANTHAN M,SRINIVAS V.Structural Damage Identification Based on Finite Element Model Updating[J].Journal of Mechanical Engineering and Automation,2015,5(3B):59-63.
[13] 钟颖.基于静力测试数据的桥梁结构有限元模型修正[D].成都:西南交通大学,2009.
[14] 叶青,胡美.基于荷载试验的大跨斜拉桥有限元模型修正方法研究[J].佳木斯大学学报:自然科学版,2015,33(3):391-394.
[15] 张征文,李永庆.基于荷载试验数据修正桥梁结构有限元计算模型的研究[J].西安建筑科技大学学报:自然科学版,2014,46(2):233-240.
[16] 李国豪.桥梁结构稳定与振动(修订版)[M].北京:中国铁道出版社,2002.
[17] 李黎,廖萍,龙晓鸿,等.薄壁高墩大跨度连续刚构桥的非线性稳定分析[J].工程力学,2006,23(5):119-124,88.
[18] 宋智,孙强.基于模型修正的桥梁极限承载力分析[J].水利与建筑工程学报,2015,13(5):228-232.
Study on Static Load Test and Bearing Capacity of Large-span Curved Continuous Rigid Frame Bridge
WANGWei1,2,3,JINGuosheng2,FENGLongcheng1,ZHANGYuping4
( 1.Chongqing Zhongshe Engineering Design Co.,Ltd., Chongqing 400025, China;2.Chongqing Zhongjian Construction Engineering Quality Testing Co.,Ltd., Chongqing 400025, China;3.School of Civil Engineering,Southwest Jiaotong University, Chengdu 610031, China;4.School of Civil Engineering and Architecture,Changsha University of Science & Technology, Changsha 410064, China )
A large-span curved continuous rigid frame bridge in national highway was taken as the research object, firstly the finite element model was established and static load test was carried out to obtain the structure deflection and strain variation in the load test, then least squares principle was combined with measured data and the model correction technology was used to modify the initial theoretical model, lastly bearing capacity of the structure had been studied on this basis. It was shown that, the bridge was in the range of flexible working, and the overall performance was good, besides, the modified model could reflect the current state of the bridge and the bearing capacity met code requirement.
continuous rigid frame bridge; static load test; model updating; bearing capacity
2016-03-21
国家自然科学基金项目(51378080);长沙理工大学土木工程优势特色重点学科创新性项目(15ZDXK02)
王 伟(1988-),男,湖北襄阳人,工程师,硕士,主要从事桥梁检测与承载能力评定及大跨度桥梁抗震减震方面的研究,(E-mail)wangweiloving@126.com
1673-1549(2016)04-0069-05
10.11863/j.suse.2016.04.15
U446;TU312
A
