弹性力学状态变量体系下各向异性层合板的稳定问题
2016-11-28李俊永吕和祥
李俊永, 吕和祥
(1.西南科技大学土木工程与建筑学院, 四川绵阳621010;2.大连理工大学工业装备结构分析国家重点实验室, 辽宁大连116023)
弹性力学状态变量体系下各向异性层合板的稳定问题
李俊永1, 吕和祥2
(1.西南科技大学土木工程与建筑学院, 四川绵阳621010;2.大连理工大学工业装备结构分析国家重点实验室, 辽宁大连116023)
通过在Hellinger-Reissner广义势能中引入应变的非线性项,推导出了弹性力学Hamilton体系下的屈曲基本方程。运用精细积分法分别对三种层合板进行求解,并与Kirchhoff解、有限元解作了比较。结果是严格弹性力学意义(没有引入任何几何变形假设)下的精确解。为衡量各种计入剪切变形的薄板、中厚板理论的准确性提供了一个标准;同时对层合板的设计具有现实的指导意义。
临界应力;精细积分法;状态空间;层合板;各向异性材料
引言
矩形板的屈曲是一个多世纪以来固体力学领域中的一个重要课题,得到了很多各向同性线弹性薄板的精确解[1-2]。各向异性板和层合板的精确解和近似解[3]也得到推导。然而,这些理论都是基于薄板理论假设,忽略了剪切变形的影响,因此只是对一定厚度范围内的板才是有效的。
Reddy J N[4]和Whitney J M[5]运用剪切变形板理论给出了厚板的解。Wang C M[6]研究了考虑剪切变形影响的各向同性简支板(Mindlin板)在面内荷载作用下的弹性屈曲问题。LIN Zhongqin和ZHANG Jianwu[7]运用卡曼方程,考虑任意叠层和材料特性,研究了矩形层合板的屈曲行为。Kim K D[8]用有限元法对层合板进行了屈曲分析,用一阶板理论考虑了横向剪切变形的影响。Matsunaga H[9]研究了四边简支厚板在面内应力下的屈曲稳定,也考虑了剪切变形的影响,并给出了厚板屈曲载荷和屈曲位移模型。Wang S和Dawe D J[10]基于一阶剪切变形理论和经典板理论,运用有限条法研究了棱状板结构的屈曲应力。Mohammad Ali Kouchakzadeh和Hideki Sekine[11]基于有限元法用Mindlin板单元分析了矩形层合板的屈曲,通过解特征值问题得到了屈曲载荷和波形。Vuksanovic Dj[12]基于高阶剪切变形板理论发展了有限板单元。Xiang Y[13]基于经典板理论(Kirchhoff板理论),运用Levy法和状态空间法得到了比较精确的屈曲载荷。Dawe D J[14]基于一阶剪切变形理论和经典板理论,用有限条法分析了层合结构的屈曲问题。
通过对以上文献分析可以看出,高阶剪切变形板理论要比低阶剪切变形板理论更加精确,但这些结果与弹性力学精确解有多大的差别还不得而知。本文参考Richard H Gallagher的成果[15],通过在Hellinger-Reissner变分原理[16-17]中引入非线性应变项,推导出了状态空间下求解临界应力的控制方程。该控制方程没有引入任何几何变形假设。由于状态空间向量由位移和应力构成,所以保证了层合板层间位移和应力的连续性。并且应用精细积分法[18]对控制方程进行求解,比有限差分法更加精确,所得结果可作为弹性力学精确解。
1控制方程

图1层合板的几何模型
图1为本文考虑的层合板的几何模型。
为方便起见,首先将一些符号注释如下:
σ:状态空间向量中的应力分量 (σ τ1τ2)。
u:状态空间向量中的位移分量 (u v w)。
S:层板局部坐标系下材料柔度阵。
C:层板局部坐标系下材料刚度阵。

A:坐标转换矩阵。
E1,E2,E3:纤维主方向上的弹性模量。
G12,G23,G13:纤维主方向剪切模量。
u,v,w:总体坐标系x、y、 z方向的位移。
x,y,z:总体坐标系。
θ:从总体坐标系x轴到纤维主方向的角度。
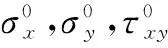
νij:泊松比,即在j方向施加单位应变,在i方向引起的横向应变。
将各向异性材料主方向定义为1、 2 、 3 ,如图1所示,则材料主方向上的应力应变关系可表示为:
ε=S·σL
(1)
或
σL=C·ε
(2)
其中:
对于角铺设层合板(见图1,材料主方向3与z轴一致),任意层的应力应变关系可表示为:
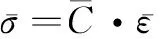
(3)
其中:
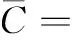
A-1·C·(A-1)T
l1=cosθ,m1=sinθ,l2=-sinθ,m2=cosθ
类似于文献[15]的推导,将三维问题应变
代入三维Hellinger-Reissner变分原理[16],变分后得到求解各向异性层合板临界应力的控制方程
(4)
其中:


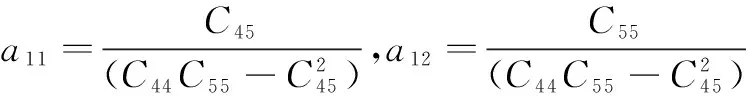

2控制方程的应用
代入方程(4)可得
(5)
其中:
p=mπ/a,q=nπ/b
应用精细积分法[18]对方程(5)求解可得
(6)
uh=T11u0+T12σ0,σh=T21u0+T22σ0
(7)
将板的上下边界条件σh=σ0=0代入方程(7)可得
T21u0=0
(8)






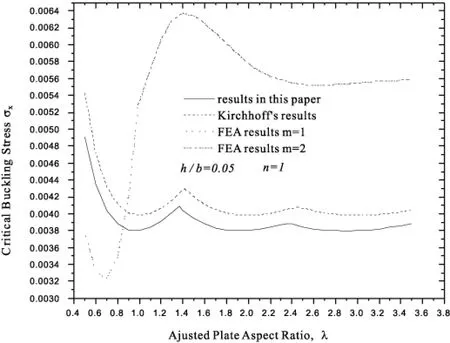

由图2~图4可知,本文结果均小于Kirchhoff解和有限元解,Kirchhoff解与本文解更接近一些。当λ较小时,三种方法所得结果较接近;随着λ的增大,差距也随之增大。由此可知,当λ较大时,有限元法所得结果误差较大。
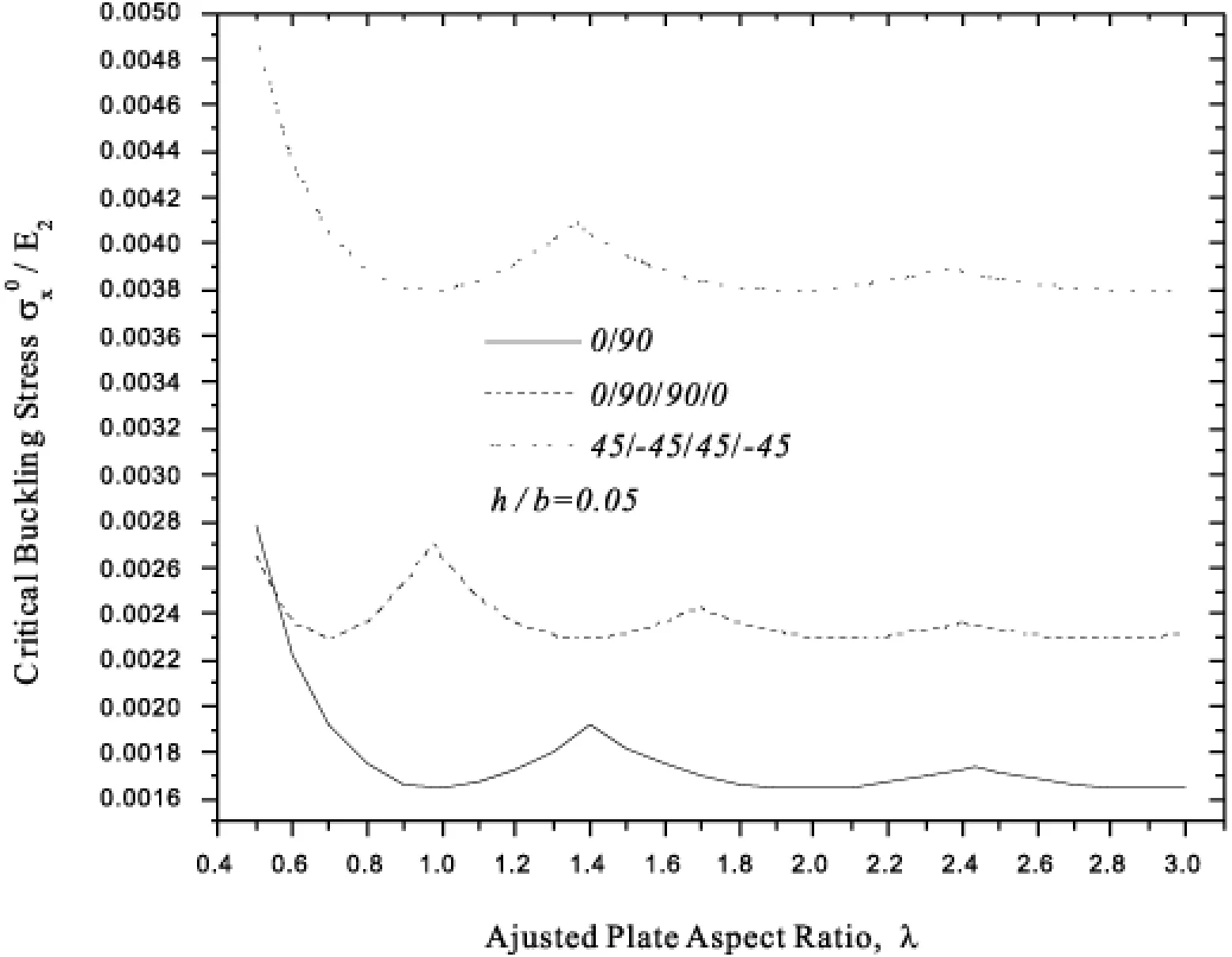

由图5 可知,层合板厚度一定的情况下,层数越多临界应力越大;而在层数相同的情况下,按45°/-45°/45°/-45°铺设的层合板要比按0°/90°/90°/0°铺设的层合板临界应力大。这个规律对于层合板的设计具有现实的指导意义。
3 结束语
本文控制方程的推导没有引入任何几何假设,是完全弹性力学意义下的屈曲方程;并且用精细积分这种高精度的数值方法进行求解。因此,本文所得结果是完全弹性力学意义下的精确解,具有重要的参考价值。
[1] TIMOSHENKO S P,WOINOWSKY-KRIEGER S.Theory of plates and shells[M].New York:McGraw-Hill,1959.
[2] TIMOSHENKO S P,GERE J M.Theory of Elastic Stability[M].New York:McGraw-Hill,1961.
[3] LEKHNITSKII S G.Anisotropic plates[M].New York:Gordon and Breach Science Publishers,1968.
[4] REDDY J N.A refined nonlinear theory of plates with transverse shear deformation[J].International Journal of Solids & Structures,1984,20(9-10):881-896.
[5] WHITNEY J M.Structural analysis of laminated anisotropic plates[M].Lancaster:Technomic Publishing,1987.
[6] WANG C M.Allowance for prebuckling deformations in buckling load relationship between Mindlin and Kirchhoff simply supported plates of general polygonal shape[J].Engineering Structures,1995,17(6):413-418.
[7] LIN Zhongqin,ZHANG Jianwu.Buckling and postbuckling of shear-deformable rectangular plates of composite construction[J].Thin-Walled Structures,1996,26(3):213-221.
[8] KIM K D.Buckling behaviour of composite panels using the finite element method[J].Composite Structures,1996,36(1-2):33-43.
[9] MATSUNAGA H.Buckling instabilities of thick elastic plates subjected to in-plane stresses[J].Computers & Structures,1997,62(1):205-214.
[10] WANG S,DAWE D J.Spline finite strip analysis of the buckling and vibration of composite prismatic plate structures[J].International Journal of Mechanical Science,1997,39(10):1161-1180.
[11] KOUCHAKZADEH M A,SEKINE H.Compressive buckling analysis of rectangular composite laminates containing multiple delaminations[J].Composite Structures,2000,50(3):249-255.
[12] VUKSANOVIC D.Linear analysis of laminated composite plates using single layer higher-order discrete models[J].Composite Structures, 2000,48(1-3):205-211.
[13] XIANG Y,WANG C M.Exact buckling and vibration solutions for stepped rectangular plates[J].Journal of Sound & Vibration,2002,250(3):503-517.
[14] DAWE D J.Use of the finite strip method in predicting the behaviour of composite laminated structures[J].Composite Structures,2002,57(1-4):11-36.
[15] Richard H G.Finite element analysis[M].New Jersey:Prentice-Hall,INC.Englewood Cliffs,1975.
[16] 胡海昌.弹性力学的变分原理及其应用[M].北京:科学出版社,1981.
[17] 唐立民,褚致中,邹贵平,等.混合状态 Hamiltonian 元的半解析解和叠层板的计算[J].计算力学学报,1992,9(4):347-360.
[18] 钟万勰.计算结构力学与最优控制[M].大连:大连理工大学出版社,1993.
Stability Problems of Anisotropic Laminated Plates Based on Exact Elasticity Theory in State Space
LIJunyong1,LVHexiang2
(1.School of Civil Engineering and Architecture, Southwest University of Science and Technology,Mianyang 621010, China;2.State Key Laboratory of Structural Analysis of Industrial Equipment, Dalian University of Technology, Dalian 116023, China)
By considering the nonlinear term in Hellinger-Reissner variation principle, the buckling formulation in Hamilton system is derived. Three laminated plates are investigated in the precise integration method. The results are compared with Kirchhoff and FEA results. The results show that the exact solutions based on the exact elasticity theory (without any geometrical hypothesis) are obtained, and a standard for both thin plates and moderately thick plates theory considering the effect of shear deformation is provided according to the results. At the same time, it is of great realistic significance for the design of laminated plates.
critical stress; precise integration method; state space; laminated plates; orthotropic materials
2016-03-24
李俊永(1973-),男,天津宁河人,讲师,博士,主要从事固体力学方面的研究,(E-mail)ljyswust@aliyun.com;
吕和祥(1938-),男,辽宁盖县人,教授,博导,主要从事固体力学方面的研究,(E-mail)lhxdlut@163.com
1673-1549(2016)04-0021-05
10.11863/j.suse.2016.04.05
O343.9
A
