经验模态分解在高层建筑GPS变形监测分析中的应用

王欣，余志奇，刘仁龙，邢诚

(1.武汉市政工程设计研究院有限责任公司，湖北 武汉 430015； 2.深圳市勘察测绘院有限公司，广东 深圳 518028；3.武汉大学测绘学院，湖北 武汉 430079)



经验模态分解在高层建筑GPS变形监测分析中的应用

王欣1*，余志奇1，刘仁龙2，邢诚3

(1.武汉市政工程设计研究院有限责任公司，湖北 武汉 430015； 2.深圳市勘察测绘院有限公司，广东 深圳 518028；3.武汉大学测绘学院，湖北 武汉 430079)

经验模态分解是一种数据驱动的自适应分解方法，能够把数据信号分解为具有自然物理意义的内蕴模态函数，有效分解各个周期的变形信号，相对小波分析等方法有其固有优势。本文针对某高层建筑物的GPS变形监测时间序列，采用EMD分解方法分离得到了建筑物的日周期、半日周期、整体趋势等多个方面振动特征，符合实际变形信号特征，验证了该方法在变形监测分析中的实用性。

EMD；高层建筑；GPS；变形监测

1 引 言

对高层建筑、大型桥梁等的变形监测手段主要有自动跟踪全站仪、倾斜仪、加速度计、激光干涉仪等。这些观测手段在室外进行高精度变形监测时都存在一些局限，难以实现实时动态监测、实时传输、连续工作[1]。GPS观测方法具有全天候、实时传输、受天气影响小、无需通视等优点，非常适用于长时间自动化变形监测。现今大型结构建筑物的高精度变形监测已经成为工程监测领域的热点。GPS监测数据中含有较多噪声，频谱分析、小波分析等方法在此类问题中得到了广泛应用[2]。但是小波分析依赖于小波基的选取，分析结果并不稳定。经验模态分解(EMD)方法是一种数据驱动的自适应数据分析方法，能够把数据信号分解为具有自然物理意义的内蕴模态函数(IMF)。本文利用EMD方法对高层建筑GPS监测数据进行了分解，获得了清晰的高层建筑变形不同周期信号。

2 EMD简介

经验模态分解(EMD)是一种与小波分析类似的局部信号特征分解的方法，具有多分辨的优点，同时克服了小波分析中对小波基选取的依赖和分解尺度的不确定性，属于一种自适应信号分解的方法[3，4]。EMD的前提假设为：任何一种信号都是一组固有模态函数(IMF)组成的，而且每一个固有模态函数都是相互独立的。从序列中分解出的分量满足以下两个条件即为IMF分量：①极值点个数和零点个数相同或者至多相差1。②上包络线和下包络线关于时间轴对称，即包络线平均值为0。以上两个条件称为固有模态分量(IMF)条件。对某一GPS监测序列x(t)，采用EMD方法的分解步骤为[5]：

(1)识别监测序列信号中极大值点并对其进行包络线eup(t)拟合；

(2)识别监测序列信号中极小值点并对其进行包络线elow(t)拟合，计算上下包络线的平均值；

(1)

(3)将原始信号x(t)减去m1(t)得到n1(t)，并将n1(t)当作新的信号x(t)，重复步骤(1)和步骤(2)，这样经过k次循环，直到n1(t)=x(t)-m1(t)满足固有模态分量条件，这时记h1(t)=n1(t)，则h1(t)为变形监测序列中的第一个IMF分量。

从原始监测序列中得到IMF分量h1(t)后，剩余信号为：

r1(t)=x(t)-h1(t)

(2)

将剩余分量r1(t)重新作为原始数据x(t)，继续重复步骤(1)～步骤(3)得到其他IMF分量，则高层建筑GPS监测序列可以被分解为：

(3)

EMD分解终止条件为：若emax、emin分别为上、下包络线，设：

(4)

设三个限值为θ1、θ2、α，相应的分解终止条件为：

(1)δ(t)<θ的时刻个数与全部持续时间之比小于1-α，即

(5)

其中D是时间序列长度，函数S{A}为集合A中元素的个数；θ1设定为0.05，α设定为0.05。

(2)或者对每个时刻t都有

δ(t)<θ2，θ2=10θ1

(6)

3 EMD在GPS监测数据处理中的应用

3.1 GPS监测数据EMD分解

本文基于某高层建筑GPS变形监测时间序列，采用EMD方法进行处理以验证其实用性。GPS观测的采样率为 30 s，总观测时间长度为 10 d。因为X和Y方向数据特征非常相似，H方向数据质量稍差，故仅采用X方向数据进行处理。图1为X方向的原始数据。从图中可以看出，X方向偏移范围约为[-6，10]，个别数据存在粗差，且噪声较多。

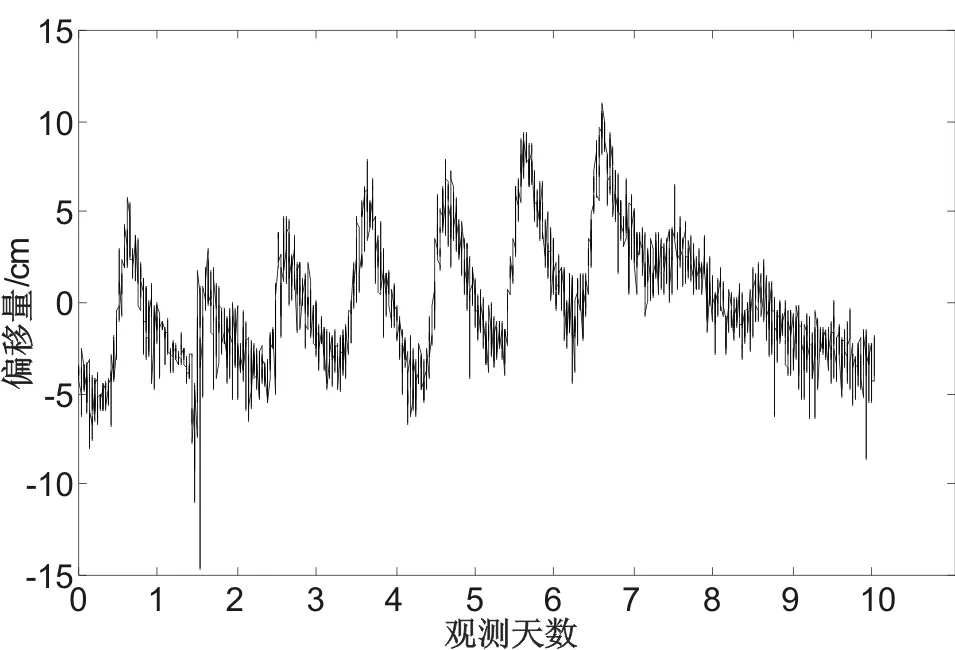
图1 X方向原始观测序列

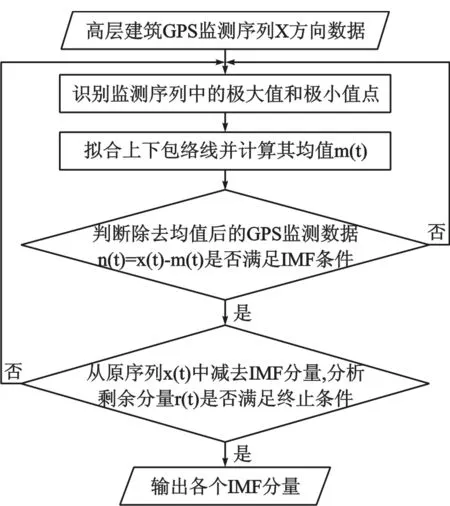
图2 GPS监测序列X方向数据EMD分解流程图

根据EMD分解原理，将该高层建筑的GPS变形监测序列X方向数据进行EMD分解。具体步骤如图2中流程图所示。首先识别X方向序列中的极大值和极小值点，然后根据这些极大值和极小值点拟合上包络线和下包络线。计算上下包络线的均值并判断去掉均值后的剩余分量是否满足IMF条件。逐步分解出X方向序列中的各个IMF分量直到达到EMD分解终止条件。最后X方向序列被分解为多个IMF分量和一个剩余分量。

3.2 结果分析

图3给出了EMD的6个分解结果，其中a～e为IMF分量，f为剩余分量。从图3中可以看出，每个IMF分量的形态和频率都不相同，反映了该高层建筑不同周期的振动特性。其中(a)子图具有明显的日周期波动，且波动幅度较大，该分量反映了高层建筑随着太阳日周期的变化；(b)子图比较平稳，在前7天一直处于缓慢上升状态，在后3天突然出现下降趋势，与原始数据中的整体趋势非常符合；(c)子图具有稳定的半日周期，反映了高层建筑的半日周期的变化；(d)和(e)子图都代表了高层建筑受到温度变化、风力等作用的影响；(f)子图为剩余信号，频率较高且没有规律，幅度较小，为GPS观测过程中的噪声。

图3 EMD分解结果

4 结 论

本文详细介绍了经验模态分解的原理以及相对于频谱分析、小波分析的优点。并利用该方法对某高层建筑的GPS变形监测序列进行分解，获得了反映建筑物日周期、半日周期、整体趋势以及观测噪声等多个方面的特征信号，获得了很好的应用效果。说明经验模态分解能够很好地分离真实变形数据和噪声以及能够将不同频率变形信号进行分解，具有一定的实用价值。

[1] 王中元，周天强，张鹏飞. 高层建筑物GPS动态变形监测数据处理[J]. 测绘科学，2012，37(1)：47～50，37.

[2] 殷文彦，黄声享，刁建鹏. 超高层倾斜建筑周日变形监测数据分析[J]. 测绘信息与工程，2008，33(2)：19～21.

[3] 王文波，张晓东，汪祥莉. 基于独立成分分析和经验模态分解的混沌信号降噪[J]. 物理学报，2013，62(05)：50201～050201.

[4] 叶林，刘鹏. 基于经验模态分解和支持向量机的短期风电功率组合预测模型[J]. 中国电机工程学报，2011，31(31)：102～108.

[5] 罗飞雪，戴吾蛟，唐成盼等. 参考经验模态分解-独立分量分析及其在GPS多路径误差处理中的应用[J]. 测绘学报，2012，41(3)：366～371.

Application of Empirical Mode Decomposition in GPS Deformation Monitoring Analysis of High Rise Building

Wang Xin1，Yu Zhiqi1，Liu Renlong2，Xing Cheng3

(1.Wuhan Municipal Engineering Design & Research Institute Co.，Ltd. Wuhan 430015，China；2．Shenzhen Geotechnical Investigation & surveying Institute Co. Ltd. Shenzhen 430079，China；3.School of Geodesy and Geomatics，Wuhan 430079，China)

Empirical mode decomposition is a data driven adaptive decomposition method，which can effectively decompose the data signals into intrinsic mode functions with natural physical meaning，and get multi-period cycles. It has inherent advantages relative to the wavelet analysis method. In this paper，take the GPS deformation monitoring time series of high-rise buildings as example，the EMD decomposition method is used to get the vibration features in the diurnal，semidiurnal period，and the linear trend，which is in accordance with the actual deformation characteristic signal. That verify the practical applications of EMD method in the deformation monitoring and analysis.

EMD；high-rise building；GPS；deformation monitoring

1672-8262(2016)05-102-03

P228，TU196.1

B

2016—04—08

王欣(1982—)，男，工程师，主要从事轨道交通工程测量和变形监测方面工作。

精密工程与工业测量国家测绘地理信息局重点实验室开放基金重点项目(PF2015-1)