基于EMD和样本熵的脑电信号睡眠分期研究❋

李怀胜，杨　芳，钟清华

（华南师范大学物理与电信工程学院，广州510006）

基于EMD和样本熵的脑电信号睡眠分期研究❋

李怀胜，杨芳，钟清华

（华南师范大学物理与电信工程学院，广州510006）

对于睡眠脑电的人工分期仍有不足的问题，提出一种基于脑电节律经验模态分解和样本熵结合的睡眠分期方法。首先利用经验模态分解对睡眠脑电信号进行去噪和基本节律提取，获得针对不同睡眠状态下脑电节律的样本熵，通过统计其样本熵均值，发现脑电节律δ波和θ波于不同睡眠状态下，样本熵均值不相等且方差较小，能有效表示不同睡眠阶段的特征，说明样本熵方法能较好的实现脑电信号的特征提取，用来区分睡眠各分期，为利用睡眠进行监护与医学治疗提供了一种可行的方法。

经验模态分解；脑电节律；特征提取；样本熵；睡眠分期

1　引　言

脑电（Electroencephalogram，EEG）是神经系统产生的可测电生理信号，包含着大量生理信息，要从睡眠脑电中进行睡眠分期有很大难度。一是睡眠时脑电信号极其微弱，易于引入干扰；二是睡眠脑电信号为非平稳随机信号，难于提取特征，因此需要利用有效手段对睡眠脑电信号进行处理。而基于脑电的特征提取方法用于睡眠深度监测，对睡眠进行合理分期，是研究睡眠质量、诊断睡眠疾病的基础。近年来基于神经网络［1－3］的方法被较多用于脑电模式识别中，此类方法的缺陷在于神经网络隐层节点数难以确定，泛化能力差，且容易陷入局部最小点。近来非线性动力学和混沌理论的方法，如：分形维数［4］、Kolmogorov－Sinai熵［5］、谱熵［6］、近似熵（ApEn）［7］等也被逐步应用于脑电等生理信号分析。这些方法各有特点，其中近似熵属于复杂度测度方法，对短数据集有效，但是近似熵值对不同参数值的选取不具备相对一致性。本文提出一种将经验模态分解（Empirical Mode Decomposition，EMD）与样本熵（Sample Entropy，SampEn）相结合的方法对睡眠脑电进行处理及睡眠分期，并经试验证明了该方法的有效性。

2　经验模态分解和样本熵理论分析

2．1经验模态分解原理

EMD方法［8］是由Huang等于1998年提出的一种新的数据处理方法，它的特点是能够对非线性、非平稳信号进行线性化和平稳化处理，并在分解过程中保留数据本身的特性，非常适合提取非线性非平稳信号的瞬时特征。EMD的本质是通过信号的时间尺度来获得本征波动模式，然后以此为依据分解信号，分解所用的基函数是基于信号本身的，它回避了小波分解中选择小波函数和分解层数的困扰，能自适应地将信号分解为一系列的表征信号特征时间尺度的固有模态函数（Intrinsic Mode Function，IMF）集。

2．2EMD分解的实现过程

信号经EMD分解后自适应的得到有限个IMF分量和一个表征信号趋势的余量，它的分解基于以下三个假定条件：①信号至少存在两个极值点，即一个极大值点与一个极小值点；②信号的特征时间尺度由相邻的两个极值点之间的时间间隔来定义；③假使信号没有极值点而只有拐点，则应当在分解之前先对信号作一次或多次微分运算来获取极值点。

EMD分解的实质是通过一种筛选来实现对信号的分解，设信号X（t）筛选的具体过程如下：

（1）寻找信号局部的所有极大值和极小值；

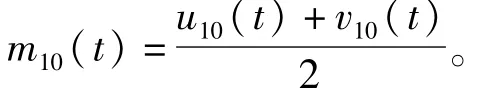
（3）计算X（t）与m10（t）的差，记做h10（t），即h10（t）＝X（t）－m10（t）。

以上过程记做一次筛选，筛选的目的有两个：去除模态波形的叠加；平滑对称模态波形的振幅。第一个目的是为了让IMF的瞬时频率具备物理意义，第二个目的是为了让两个相邻的IMF振幅差不至于太大，使得IMF具备调频作用。

（4）检查h10（t）是否满足IMF条件。如果不满足，则将h10（t）代替原始信号X（t），重复k次以上步骤，直至h1k满足IMF条件。这样就得到了原始信号X（t）的第一个IMF，记做c1（t），即c1（t）＝h1k（t）。

（5）将c1（t）从原始信号X（t）中分离出来，得到剩余分量r1（t），即r1（t）＝X（t）－c1（t）。

（6）将r1（t）代替原始信号X（t）依次重复以上步骤，对后面的rk（t）也同样做筛选，分解出新的IMF集，即r2（t）＝r1（t）－c2（t）．．．rN（t）＝rN－1（t）－cN（t）。

当rN（t）是一单调函数或者小于预先设置的值时，EMD的整个分解过程将停止。为了使得IMF在幅值和频率上同时具备物理意义，Huang设置了一个基于限定相邻两个筛选结果的标准偏差SD的筛选准则，即：

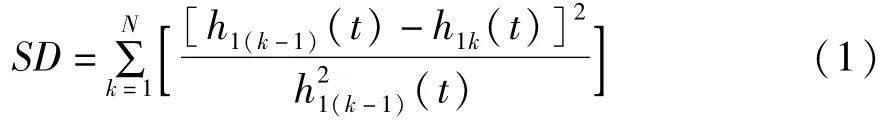
当SD的值为0．2－0．3之间时，则终止筛选。

综上，在EMD的整个筛选过程中，基函数是基于信号本身的特性而自动生成的，信号特性不同，其基函数也不同，因而EMD是根据信号本身的特性而对信号做自适应的分解。信号经过EMD分解后得到有限个IMF分量，每个IMF分量则凸显了信号的内在物理信息，这些IMF分量的截止频率随着信号的变化而变化。

2．3样本熵

样本熵是量化时间序列复杂性和研究时间序列性质的重要工具，被广泛应用于很多研究领域，特别是生物医学信号的研究与分析，其算法［13］描述如下：

（1）对于一个N点的时间序列，我们表示为u＝｛u（1），u（1），．．．u（N）｝。

（2）按序号连续顺序组成一组m维向量：Xm（1），Xm（2），．．．，Xm（N－m＋1），其中Xm（i）＝［u（i），u（i＋1），．．．，u（i＋m＋1）］，1≤i≤N－m＋1。

（3）定义两个m维向量Xm（i）和Xm（j）之间的距离d［Xm（i），Xm（j）］为两者对应元素中差值最大的一个，即：d［Xm（i），Xm（j）］＝max｛｜u（i＋k）－u（j＋k）｜｝，其中0≤k≤m－1，1≤i≤N－m＋1，1≤j≤N－m＋1，i≠j。

（4）r是设定的匹配过程公差阈值，给定一个阈值r，对每一个i≤N－m＋1的值，统计d［Xm（i），Xm（j）］小于r×SD（SD为序列的标准差）的数目Nm（i），并计算此数目与距离总数（N－m）的值，记作：Cm（r）＝Nm（i）／（N－m）。

（7）样本熵定义为：

当N为有限值时，按上述步骤得出的是序列长度为N时样本熵的估计值，记作：

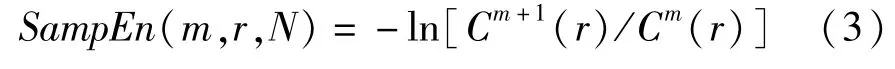
样本熵的物理意义是表示非线性动力学系统产生新信息的速率，样本熵值越小，序列自我相似性越高；样本熵值越大，序列越复杂。对于SampEn（m，r，N）函数，Pincus建议r的值取0．1－0．25SD，SD为要计算的时间序列标准差，m取1或2，参数N是数据长度，要得到有效的统计特性和比较小的伪差，数据点数最好在100－5000之内。通过实验验证，参数设为m＝1，r＝0．2SD，N＝1500时，处理睡眠脑电信号得到的样本熵值分布效果最好。

3　方法与实验结果

3．1实验数据

实验数据来源于麻省理工学院提供的MITBIH中的The Sleep－EDF database，所用数据编号为SC4001E0－PSG，1989年4月24日14：13：00～4月 25日14：18：00的睡眠数据。数据采样频率为100Hz，波幅单位为μV；数据存储格式为欧洲数据格式；参考导联为Fpz－Cz和Pz－Oz；该睡眠脑电的睡眠期已由专家人工标注。

3．2睡眠脑电的去噪处理

MIT－BIH数据库中的原始脑电信号含有大量的眼电、肌电、工频、高频、白噪声等干扰，消除脑电信号中的噪声是进行睡眠分析的重要前提［14］。

（1）基于EMD滤波的EEG去噪

任意信号经过EMD算法分解后会得到有限个IMF分量和一个表征信号趋势的残余分量。这些IMF分量总是按照由高频到低频的顺序逐渐分离出来，表征了信号频率分布的所有信息，因而它是一种自适应滤波的信号分析方法。基于EMD算法的分解特性，可以将EMD看做是一个时频滤波的分析方法［15］。

基于EMD滤波的思想十分简单，即根据信号的要求，通过去除噪音频段的IMF，将剩余的IMF重构来增强信号在要求频率范围内的特征。其优点在于，EMD的基函数直接从信号本身产生，不像小波分解算法那样需要预先确定基函数，它是一种基于信号局部特征尺度分解的自适应滤波法。选取实验数据中一段脑电信号进行去噪处理，如图1所示，滤除噪音后的信号，白噪声与尖波脉冲干扰基本消除，与此同时很好的保留了有用信号中的尖峰和突变部分，滤波处理是为下一步分析脑电信号作好准备。

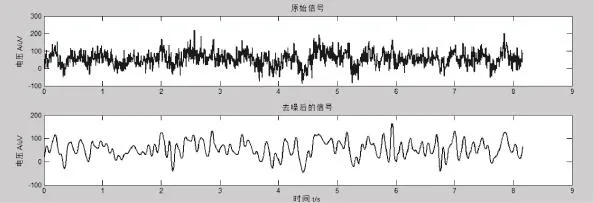
图1　脑电信号滤波处理

3．3睡眠脑电基本节律的提取

通过信号的时间尺度来获得本征信号波动模式，然后以此为依据分解信号，分解所用的基函数是基于信号本身的。再对非线性、非平稳信号进行线性化和平稳化处理，具有良好的时频局部化特性，可实现对信号瞬态成分的检测，并可对其各频率段成分进行处理，提取到睡眠脑电信号节律的时变信息，并在分解过程中保留数据本身的特性，较好地表现频域信号的连续性和突变性，在实际工程应用中能够获得较好的效果。选取实验数据中的一段睡眠脑电信号，如图2所示。脑电信号基本节律的提取，如图3所示，图4为完备性检测图。

3．4睡眠脑电基本节律的分析

目前国际上普遍使用的是R＆K睡眠分阶规则［16］，它把睡眠分为觉醒期（SW）、非快速眼动睡眠期（NREM）、和快速眼动睡眠期（REM），其中NREM可分为Ⅰ期、Ⅱ期、Ⅲ期和Ⅳ期。由于Ⅲ期和Ⅳ期波形很相似，仅在振幅上略有区别，将Ⅲ期和Ⅳ期统一划分为Ⅲ期。且δ波和θ波是表征睡眠的主要特征，因此将重点分析基本节律中δ波和θ波的变化。

图2　原始睡眠脑电信号

图3　脑电信号基本节律提取

图4　脑电各基本节律的完备性检验

根据脑电信号在不同睡眠状态下脑电基本节律的表现不同，通过比较睡眠各期的脑电节律δ波和θ波样本熵值的大小，可用来区分不同的睡眠状态。实验中以实验数据库中的分期结果为参考标准，利用matlab进行数据处理，分别任意截取觉醒期（SW）、快速眼动睡眠期（REM）和非快速眼动睡眠期（NREM）Ⅰ期、Ⅱ期、Ⅲ期的睡眠脑电数据，分别对其进行去噪和基本节律提取，然后对睡眠实验室数据进行样本熵计算，取m＝1；r＝0．25SD；N＝1500，并参考经验丰富的医生所做的人工睡眠分期的结论，得到睡眠脑电基本节律δ波和θ波样本熵的平均值，再统计方差，得到睡眠各期脑电节律的样本熵均值与方差如图5－图6所示。

图5　睡眠各期脑电节律的样本熵均值

图6　睡眠各期脑电节律的样本熵方差

从睡眠规律的角度来看，睡眠各期的样本熵是不一样的，随着睡眠的深入，δ波和θ波的样本熵均值逐渐增大，δ波和θ波复杂性增强，这与有睡意时脑电中δ波和θ波占主导相吻合［17］。清醒期脑电节律以大于8Hz为主，所以清醒期的δ波和θ波样本熵均值最小；快速眼动期虽然是处于深睡期，但大部分时间在做梦，所以该期的样本熵均值最大。而从样本熵均值及方差大小的角度来看，睡眠各期脑电节律δ波和θ波的样本熵均值都不相等，样本熵均值的方差很小，即不同睡眠状态下的脑电节律δ波和θ波样本熵值波动范围小，总能找出任一个睡眠期与其它睡眠期的δ波和θ波样本熵均值不相等，并且能较容易区分不同的睡眠状态。综上，通过脑电节律样本熵的方法可以用来区分睡眠各期。

4　结束语

与脑电的非线性分析方法比较，结合EMD和样本熵的方法可以更完整的提取睡眠脑电的各个节律，较好的保留其信号本身的特性，细致地对不同睡眠状态下脑电基本节律的变化进行分析；同时由于睡眠各期的脑电节律δ波和θ波样本熵均值的大小不相等，且样本熵均值方差很小，它们能有效表示不同睡眠阶段的特征。结论与数据库中的专家判定相吻合，这说明样本熵方法能很好的进行脑电信号的特征提取，可以用来区分睡眠各分期，可为其他信号的特征提取提供理论与实验依据，也为利用脑电信号进行监护与医学治疗提供了一种可行的方法。

［1］Shimada T，Shiina T，Saito Y．Detection of characteristic waves of sleep EEG by neural network analysis［J］．IEEE Transactions on Biomedical Engineering，2000，47（3）：369－379．

［2］Liu Derong，Pang Zhongyu，Lloyd Stephen r．A neural network method for detection of obstructive apnea and narcolepy based on pupil size and EEG［J］．IEEE Transactions on Biomedical Engineering，2008，19（2）：308－318．

［3］吴婷，颜国正，杨帮华，等．基于有监督学习的概率神经网络的脑电信号分类方法［J］．上海交通大学学报，2008，42（5）：803－806．Wu T，Yan G Z，Yang B H，et al．Electroencephalography Classification Based on Probabilistic Neural Network with Supervised Learning in Brain Computer Interface［J］．Journal of Shanghai Jiaotong University，2008，42（5）：803－806．

［4］胥永刚，何正嘉．分形维数和近似熵用于度量信号复杂性的比较研究［J］．振动与冲击，2003，22（3）：25－27．Xu Y G，He Z J．Research on Comparison betweenapproximate entropy and fractal dimension for complexity measure of signals［J］．Journal of Vibration and Shock，2003，22（3）：25－27．

［5］Pincus S M，Goldberger A L．Physiological time－se－ries Analysis：What does regularity quantify［J］．Amer J Physiol Heart Circulatory Physiology，1994，266（4）：1643－1656．

［6］Grouven U，Beger F A，Schultz B，et al．Correla－tion of narcotrend index，entropy measures，and spectral parameters with calculated propofol effect－site concentrations during induction of propofol－remifentanil anaesthesia［J］．Journal of Clinical Monitoring and Computing，2004，18（4）：231－240．

［7］Pincus S M．Approximate entropy（ApEn）as a complexity measure［J］．Chaos，1995，5（1）：110－117．

［8］Huang N E，Shen Z，Long S R，et al．The empirical mode decomposition and the Hilbert spec－trum for nonlinear and non－stationary time series analysis［J］．Proceedings of the Royal Society of London，Series A，1998，454（1971）：903－995．

［9］Soomro，M．H．A method for automatic removal of eye blink artifacts from EEG based on EMD－ICA［C］．Signal Processing and its Applications（CSPA），2013 IEEE 9th International Colloquium on，2013：129－134．

［10］J Ville．Theorie Et Applications De La Notion De Signal Analytique［J］．Cablesettransmission，1948（2）：61－74．

［11］H Kim，K Hwang1，J Cho D Koo．Effect of bedside light on sleep quality and background EEG rhythms［J］．Sleep Medicine 14S（2013）：e165－e238．

［12］Azarnoosh M，Motie Nasrabadi A，Mohammsdi M R，et al．Investigation of mental fatigue through EEG signal processing based on nonlinear analysis：symbolic dynamics［J］．Chaos，Solitons＆Fractals，2011，44（12）：1054－1062．

［13］Joshua S Richman，J Randall Moorman．Physiological timeseriesanalysisusingapproximateentropyand sample entropy［J］．Am j．physiol heart circ physiol，278：h2039－h2049，2000．

［14］Aboalayon K A I．Efficient sleep stage classification based on EEG signals［C］．IEEE Long Island Systems，Applications andTechnologyConference（LISAT），2014．

［15］P Flandrin，P Goncalves，G Rilling．Detrending and Denoising with Empirical ModeDecompositions［C］．Proc．of XII EUSIPCO 2004，Vienna，Austria，2004：1581－1584．

［16］王菡侨．有关美国睡眠医学学会睡眠分期的最新判读标准指南解析［J］．诊断学理论与实践，2009，8（6）：575－578．Wang H Q．About the latest interpretation standard of guidelines of American Academy of Sleep Medicine for sleep staging［J］．Journal of Diagnostics Concepts＆Practice，2009，8（6）：575－578．

［17］V Bajaj，R B Pachori．Automatic classification of sleep stages based on the time－frequency image of EEG signals［J］．Comput．Methods Programs Biomed，2013，112（3）：320－328．

［18］Hau－tieng Wu，Talmon R，Yu－Lun Lo．Assess Sleep Stage by Modern Signal Processing Techniques［J］．IEEE Transactions on？Biomedical Engineering，2014，62（4）：1159－1168．

［19］李治，汪曣，刘凤军，等．入睡脑电信号的去噪［J］．中国组织工程研究与临床康复，2007，11（13）：2531－2533．Li Z，Wang Y，Liu F J，et al．Noise removing in sleeping electroencephalogram signal［J］．Chinese Journal of Tissue Engineering Research，2007，11（13）：2531－2533．

［20］Huang Ch－Sh；Lin Ch－Li；Ko，et al．A hierarchical classification system for sleep stage scoring via forehead EEG signals［C］．IEEE Symposium on Computational Intelligence，Cognitive Algorithms，Mind，and Brain（CCMB），2013（5）：16－19．

［21］See，A．R．A study on sleep EEG Using sample entropy and power spectrum analysis［C］．Defense Science Research Conference and Expo（DSR），2011：1－4．

［22］L Cohen，C Lee．Instantaneous Frequency，Its Standard Deviation and Multicomponent Signals［J］．SPIE Adv．Algs．Sig．Proc．III，1988，975：186－208．

［23］Temel Kayikcioglu，Masoud Maleki，Kubra．ErogluFast and accurate PLS－based classification of EEG sleep using single channel data［J］．Expert Systems with Applications，2015（42）：7825－7830．

Study on Sleep Stages Based on EMD and Sample Entropy of EEG Rhythm

Li Huaisheng，Yang Fang，Zhong Qinghua
（School of Physics＆Telecommunication Engineer，South China Normal University，Guangzhou 510006，China）

A method of sleep stages，based on EMD and sample entropy of EEG rhythm，is put forward to solve the shortage of artificial staging of sleep EEG．Firstly，EMD is used to denoise sleeping EEG and extract the basic rhythm．Secondly，the sample entropy of EEG rhythm under different sleep states is computed．Finally，after the statistics of mean and variance of the sample entropy，the mean of sample entropy of wave δ and wave θ is different under different sleeping stages of EEG rhythm，which indicates that the sample entropy analysis of sleep EEG rhythm can be used to effectively characterize different sleeping stages and extract feature of EEG．It provides a new way to make use of sleeping EEG for care and treatment．

EMD；EEG rhytnm；Feature extraction；Sample entropy；Sleep stages

10．3969／j．issn．1002－2279．2016．05．017

TP3

A

1002－2279（2016）05－0068－05

❋广东省教育部产学研合作基金（2012B091100062）；广东省自然科学基金（S2011040003189）；广东省科技计划项目（20130123q）

李怀胜（1991－），男，广东省阳江市人，硕士研究生，主研方向：智能仪器及生理信号处理方向。

2015－12－25