基于有限元法的压力容器爆破压力预测*

王飞 邢璐 赵哲明 陈涛

（杭州市特种设备检测研究院)

基于有限元法的压力容器爆破压力预测*

王飞**邢璐 赵哲明 陈涛

（杭州市特种设备检测研究院)

针对带接管的圆柱形壳体这一压力容器的典型结构，采用有限元法对其进行爆破失效分析，预测爆破压力。将有限元法的计算结果与经验公式的计算结果进行了对比，结果显示有限元分析结果较经验公式的计算结果偏安全，是一种有效的压力容器爆破压力预测方法。采用的预测方法可为压力容器按照爆破失效准则进行设计和预测爆破压力提供参考。

压力容器 爆破压力 有限元 弧长法 失效准则

0 前言

在压力容器设计中，容器壁厚的确定看似简单，只要按照GB 150—2011《钢制压力容器》标准即可，但是在具体计算过程中却存在着设计的合理性问题。怎样使设计的产品既安全又省材，这是一个技术问题。精确的爆破压力计算值可以降低爆破失效设计准则的安全系数，提高设计精度，从而减少材料用量，减轻容器重量。爆破失效准则的理论基础是容器筒体承受的内压超过屈服极限之后，产生塑性变形，随着塑性区的扩展，塑性变形引起材料发生硬化效应以及器壁逐渐减薄。由于材质具有良好的塑性和明显的应变硬化特征，因此依照爆破失效准则设计高压容器具有很大的实际意义。这样，爆破压力的确定就是一个非常重要的问题。

福贝尔(Faupel)研究了承受内压的圆筒形容器爆破压力计算问题，同时用许多容器进行实验，建立了爆破压力经验计算公式。但福贝尔公式仍存在一些不足：一是计算爆破压力的误差在±15%左右。二是当容器材料的屈强比，即容器材料屈服强度与抗拉强度之比较低时，福贝尔公式的计算结果偏于安全；而当屈强比较高时，其计算结果偏于危险［1-5］。现今随着计算机技术的发展，有限元方法被用来预测、计算和分析压力容器的强度［6-7］。

本文针对带接管的圆柱形壳体这一压力容器的典型结构，对其进行爆破失效分析，预测爆破压力。为此类压力容器按照爆破失效准则进行设计和预测爆破压力提供参考。

1 物理模型

本文所分析的压力容器结构如图1所示。其中球形封头与筒体的过渡采用堆焊球封头的方式。该容器的基本尺寸如表1所示。容器材料为Q345R，其基本性能参数如表2所示。假设材料为弹塑性体且各向同性。

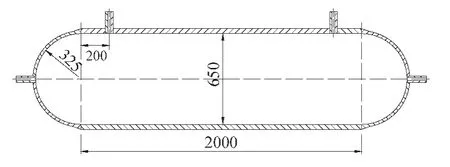
图1 容器结构

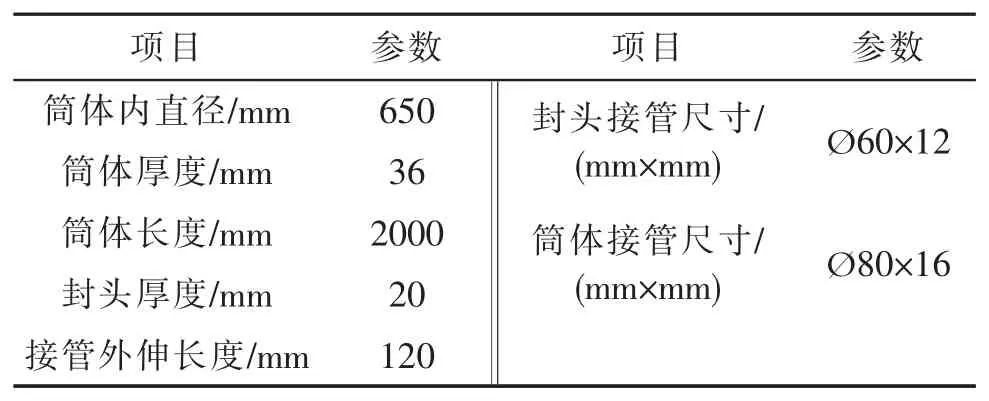
表1 容器基本尺寸

表2 材料性能参数

对于内压容器，爆破过程中，内压和容积变化量的关系与材料塑性、容器容积和壁厚有关。对于脆性材料，不会出现弹塑性变形阶段。虽然塑性垮塌压力大于爆破压力，但工程上往往把塑性垮塌压力视为爆破压力。本文也近似认为塑性垮塌压力就是爆破压力。

2 经验公式预测结果

Faupel公式形式简单，计算方便，中国、日本等国都把它作为厚壁圆筒强度设计的基本方程。本文使用Faupel厚壁圆筒爆破压力计算公式如下：

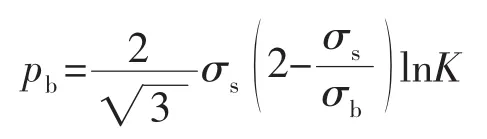
式中

爆破压力的计算结果为：pb=56.87 MPa。

3 有限元分析结果

3.1 模型和边界条件

根据结构的特点，建模时只考虑容器整体的1/4，三维模型如图2所示。

图2 待分析容器的三维模型

本文采用的网格模型如图3～图5所示。有限单元采用具有沙漏控制的减缩积分单元C3D8R。

图3 计算网格

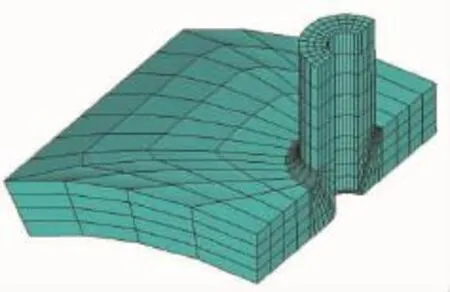
图4 筒体接管处网格

图5 封头接管处网格

有限元模型的边界条件如图6所示。

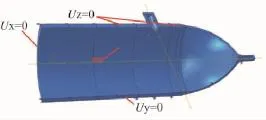
图6 载荷及边界条件

3.2 爆破压力预测

分别采用弧长法和非线性稳定性算法计算容器的爆破压力。

3.2.1 弧长法

采用弧长法得到的结构在爆破时的Mises应力云图见图7。容器的爆破压力预测结果为48.927 MPa。爆破压力与弧长关系曲线如图8所示。

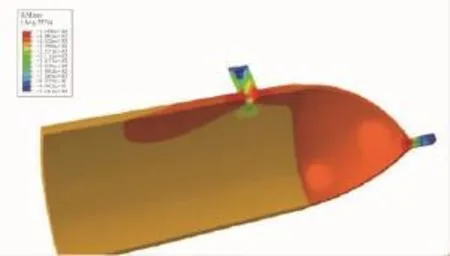
图7 容器爆破时Mises应力云图

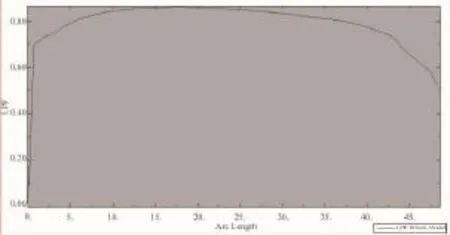
图8 爆破压力与弧长的关系曲线

3.2.2 非线性稳定性算法

采用非线性稳定性算法得到的容器整体结构的Mises应力云图如图9所示。得到容器的爆破压力为51.18 MPa。

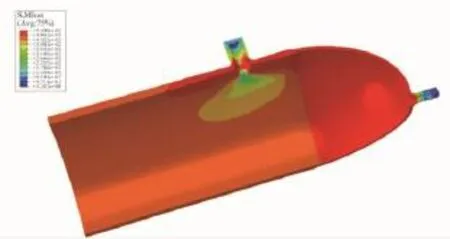
图9 非线性稳定算法得到的容器Mises应力云图

4 结论

（1）本文针对带接管的圆柱形壳体这一压力容器的典型结构，采用有限元分析方法，对其进行了爆破失效分析，预测爆破压力。

（2）采用弧长法和非线性稳定性算法预测的爆破压力结果较为相近，非线性弧长法的爆破压力计算结果较低。

（3）由有限元法的计算结果与经验公式的计算结果对比可以看出，有限元分析结果较经验公式的计算结果偏安全，并且可以直观地观察到容器各部分的受力情况，是一种直观、有效、经济的压力容器爆破压力预测方法。

[1]郑传祥,文棋.低碳钢压力容器爆破试验及爆破压力公式研究[J].压力容器,2002,19(9):9-12.

[2]郑传祥,文棋.低碳钢压力容器爆破压力公式的修正[J].化工机械,2002,29(5):275-278.

[3]柳爱群,杨中,杨烨.圆筒形压力容器爆破压力经验公式的改进[J].机械强度,2013,35(5)：652-656.

[4]刘芳,王海峰,桑芝富.轴向斜接管内压容器爆破压力的预测[J].石油机械,2009,37(2):15-18.

[5]黄载生.超高压容器爆破压力计算[J].压力容器, 1992,9(3):254-257.

[6]常新龙,张晓军,刘新国,等.复合材料气瓶有限元分析与爆破压力预测[J].火箭推进,2008,34(4):27-31.

[7]杨象岳,李伟忠,李顺荣,等.基于扩展有限元的钢瓶爆破数值仿真研究[J].深冷技术，2013(4):47－50.

Burst Pressure Prediction of Pressure Vessel Based on Finite Element Method

Wang FeiXing LuZhao ZhemingChen Tao

The blasting failure analysis and the prediction of the blasting stress of the cylindrical pressure vessel with the connecting pipe are carried out based on the finite element method.The results from the finite element method and the empirical equation are compared and it shows that the former is safer and more effectvie which provides the reference for the design of the pressure vessel according to the burst failure criterion as well as the prediction of the burst pressure.

Pressure vessel;Burst pressure;Finite element;Arc length method;Failure criterion

TQ 050.1

10.16759/j.cnki.issn.1007-7251.2016.08.012

2015-12-04）

*资助项目：浙江省质监系统科技计划项目No.20150237。

**王飞，男，1983年生，硕士，工程师。杭州市，310051。