应用不可满足子式的解码电路综合优化方法*
2016-11-28张建民黎铁军马柯帆肖立权
张建民,黎铁军,马柯帆,肖立权
(国防科技大学 计算机学院, 湖南 长沙 410073)
应用不可满足子式的解码电路综合优化方法*
张建民,黎铁军,马柯帆,肖立权
(国防科技大学 计算机学院, 湖南 长沙 410073)
解释布尔公式不可满足的原因在很多领域都具有实际的应用需求,而最小不可满足子式能够为诸如电路的自动综合等应用领域中的不可满足原因提供最精确的解释。因此,将两种能够高效求解最小不可满足子式的算法——分支-限界算法与贪心遗传算法,集成到解码电路的自动综合工具中。采用通信领域的标准编码电路作为测试集,将两种算法进行对比。实验结果表明,在运行时间与每秒剔除的短句数方面,贪心遗传算法优于分支-限界算法;不可满足子式在解码电路的自动综合过程中发挥重要作用。
电路综合;形式化方法;可满足性求解;不可满足子式
在超大规模集成(Very Large Scale Integrated, VLSI)电路芯片中,通常都会设计各种各样的编码和解码电路,尤其是在与通信相关的芯片设计过程中,往往会遇到很多非常复杂的编码与解码电路。编码电路通常根据某种规则将原始数据编码或产生校验码,常见的包括循环冗余校验(Cyclic Redundancy Code,CRC)或纠错码(Error Correction Code,ECC),而解码电路根据校验码和原始数据判定接收的数据是否正确。这些电路需要消耗设计者大量的时间来进行验证,那么,能否只设计与验证编码电路,而后通过一种自动化的方法来产生正确的解码电路,从而降低设计者的工作量?因此,产生了自动对偶综合工具[1]。自动对偶综合的基本思路是:给出一个已验证的编码电路,通过形式化的方法自动综合出一个功能正确的解码电路。对偶综合工具通过分析特定编码电路的状态空间,自动产生相应的解码电路,避免设计人员将时间花费在设计解码器上,从而降低芯片设计的风险,并加速设计进程。而在对偶综合工具中,使用不可满足子式求解器,移除冗余短句以削减状态空间,是加快整体运行速度的关键。
自动对偶综合工具的基本流程是:以编码电路的寄存器传输级(Register Transfer Level,RTL) Verilog代码和工具的参数配置作为输入,首先采用Verilog语法分析器将设计转换为内部的中间表示,而后在状态空间中进行搜索,通过合取范式(Conjunctive Normal Form,CNF)产生器得到布尔公式;再调用一种高效的SAT求解器——zChaff求解器,判定公式的可满足性。若可满足,则算法继续搜索;否则采用不可满足子式求解器提取最小不可满足子式,并将该子式作为输入,反向抽取出解码电路的RTL代码。
布尔不可满足子式求解器是自动对偶综合工具的重要组成部分。由于不可满足子式越小,越有利于反向电路提取,因此在自动对偶综合工具中主要集成了求解最小不可满足子式的算法。而在当前求解最小不可满足子式的算法中,分支-限界算法[2]与贪心遗传算法[3]是最高效的两种算法,二者的相同之处是都基于布尔公式的极大可满足性与极小不可满足性之间的关系,区别在于优化策略,前者采用确定性最优化的分支-限界算法,后者采用近似最优化的贪心遗传算法。
1 不可满足子式的定义
CNF公式的基本消解规则为:
表示为[(A∨x)∧(B∨x)](A∨B),其中x是一个变元,叫作消解元,A与B表示若干个文字的析取,(A∨x)与(B∨x)称为消解母式,而结果短句(A∨B)称为消解式。短句(x)与(x)的消解式为空短句。每次应用消解规则产生消解式叫作一个消解步骤。一系列的消解步骤,其中每一步都使用前面步骤产生的消解式或原始公式中的短句作为当前的消解短句,称为消解序列。
引理1 当且仅当存在有限个消解步骤且最终产生的消解式为空短句时,CNF公式是不可满足的。
定义1(不可满足子式) 给定一个不可满足公式φ,当且仅当ψ是不可满足的且ψφ时,ψ是公式φ的一个不可满足子式。
定义2(极小不可满足子式) 给定不可满足公式φ的一个不可满足子式ψ,当且仅当φψ且φ是可满足的时,ψ是极小不可满足子式。
对于CNF公式来说,如果一个不可满足子式是不可约的,即它的所有真子集都是可满足的,那么它是极小不可满足子式。
定义3(最小不可满足子式) 给定一个不可满足公式φ以及φ的所有不可满足子式构成的集合:{ψ1,ψ2, …,ψj}。那么当且仅当ψi∈ {ψ1,ψ2, …,ψj},1≤i≤j,使得时,ψk∈{ψ1,ψ2, …,ψj}是最小不可满足子式。
根据定义3,最小不可满足子式是公式的所有不可满足子式中长度最小的,即所包含的短句数最少。所有不可满足的布尔公式都至少包含一个最小不可满足子式。相对于不可满足子式或极小不可满足子式,最小不可满足子式往往包含一些简单消解规则所不能剔除的冗余短句,因此最小不可满足子式的求解难度更大,算法复杂度更高,但是对于应用的优化效果最佳。相对于求解极小不可满足子式的研究来讲,近年来关于如何求解最小不可满足子式的研究工作较少。
2 不可满足子式的求解算法
近年来,相继涌现出了许多求解布尔不可满足子式的研究成果。21世纪初,自从融合冲突学习机制等启发式方法的DPLL(Davis-Putnam-Logemann-Loveland)算法出现之后,SAT求解器得到了飞速的发展,因此,基于SAT求解器的不可满足子式求解方法也逐渐成了研究的主流方向。zCore[4]是一种基于高效SAT求解器产生的消解悖论来提取不可满足子式的算法,但是其结果只是小的而非极小不可满足子式。另外一个仅能求解不可满足子式的算法是AMUSE[5],该算法在增加选择变元的公式上通过增强DPLL过程搜索不可满足子式。Lynce等[6]提出了一种使用SAT求解器来穷尽搜索公式的全部空间,从而得到最小不可满足子式的算法。
Timmer算法[7]通过证明短句蕴含图中的一个结点等价于一组短句,而后删除该组短句,不断循环直到产生不可满足子式。Dershowitz等[8]利用SAT求解器产生的消解悖论,移除一个初始短句及其导致的所有冲突短句,通过检验剩余子公式的可满足性来确定该短句是否属于不可满足子式。Maaren等[9]基于Brouwer不动点定理来求解极小不可满足子式,将判定公式的不可满足性转换为从Pareto最优规则中找到一个短句的子集或并集的可能性。东南大学陈振宇等[10]提出了一种基于消解的极小不可满足子式求解算法,并应用于模型检验。吉林大学赵相福等[11]则提出了产生所有的极小不可满足子式集合的算法。
Nadel[12]提出了两种基于消解的极小不可满足子式求解算法,但在算法超时时,则仅得到非极小不可满足子式。Marques-Silva等[13]提出了两种求解极小不可满足子式的算法,第一种算法将运行时调用SAT求解器的次数最小化,第二种算法在之前工作的基础上集成了很多新的优化技术。Ryvchin等[14]在消解算法[12]的基础上提出了7种优化技术,实验表明其能够减少55%的运行时间以及73%的不可满足子式的短句数。Chen等[15]提出了通过求解不可满足子式来加速布尔公式分解的两种优化技术。Belov等[16]引入了迭代模型旋转的技术,该技术能够有效地提高求解不可满足子式的效率。该作者还借鉴了求解不可满足子式的多种优化技术,用于求解公式的最小等价子式[17]。
Liffiton等[18]提出一种新的算法用于求解多个不可满足子式,能适用于每种约束系统。Nadel等[19]将模型旋转技术应用于基于消解的极小不可满足子式求解方法中,并提出了eager旋转和路径增强技术以提高求解效率。Lagniez等[20]引入基于假设的文字参数化增量式SAT求解技术,用于加速不可满足子式的提取过程。Marques-Silva等[21]提出了基于布尔公式单调谓词的不可满足子式求解算法,并且通过实验表明,该方法属于当前最优算法。Belov等[22]引入了冲突驱动的短句学习SAT求解器中的短句证明技术,用于求解极小不可满足子式的剪枝过程。在SAT′14上,有学者[23]提出了偏好极小不可满足子式与极小正确子集的概念,并集成已有的优化剪枝技术,给出了求解算法。
下面简要地介绍一下当前两种最优的最小不可满足子式求解算法:分支-限界算法与贪心遗传算法。Liffiton等[2]提出了一种求解最小布尔不可满足子式的分支-限界算法,该算法利用极大可满足性反复产生不可满足子式的上界与下界,并在特定的子公式上分支,从而得到最小不可满足子式。该算法能够处理实际应用中较大规模的问题,例如DaimlerChrysler测试集。该算法的优点是能得到准确的最小不可满足子式,不足之处是效率都相对不高。张建民等[3]证明了最小不可满足性与极大可满足性之间的关系,并且基于二者的关系,提出一种贪心遗传算法解决从公式中提取最小不可满足子式的问题。算法的主要过程是:根据最小不可满足性与极大可满足性之间的关系,首先利用SAT求解器,通过增加短句选择因子与限界约束的方式,提取布尔公式的所有极大可满足子式;而后计算极大可满足子式补集的最小碰集,从而得到最小不可满足子式。该算法的优势是求解效率高,不足之处是对于某些公式,仅能得到近似而非精确的最小不可满足子式。
3 基于不可满足子式的解码电路综合优化方法
在VLSI电路中,尤其是在与通信相关的芯片设计过程中,往往会遇到很多非常复杂的编码与解码电路。这些电路需要满足许多特定的编码要求,如直流均衡、游程、校验、最大包长度、包间间隔、对时钟和数据偏斜的容忍度等,而这些要求在不同的应用环境中又有着完全不同的侧重点。使用单一IP核无法在所有的情况下均得到最优化的设计。满足这些编码要求的编码器和解码器需要消耗设计者大量的时间进行验证,那么,能否只设计与验证编码电路,而后通过一种自动化的方法来产生正确的解码电路,从而降低设计者的工作量?因此,产生了自动对偶综合的概念。自动对偶综合的基本思路是:给出一个经过验证的编码电路,通过形式化的方法自动综合出一个功能正确的解码电路。
通常,绝大多数的编码器都可以用一个简单的模型建模,称之为DELAY-LENGTH模型。该模型的两个参数构成一个二元组
自动对偶综合的原理如图1所示。假设编码电路表示为C,解码电路表示为C,那么可以将编码电路C沿时间轴展开n个时钟周期,构成一个新的电路Cn:Cn=C×C×…×C。根据电路Cn,构造一个与其完全相同的电路拷贝,记为。定义一个算子⊗:F=Cn⊗(表示两个电路的输入不同,输出相同,构成的电路记为F)。根据一个给定的二元组

图1 自动对偶综合的基本原理Fig.1 Principle of automatic decoder synthesis
图2给出了自动对偶综合工具的结构框图,其中粗框表示即为本文所实现的布尔不可满足子式求解器。由于不可满足子式越小,越有利于反向电路提取,因此在自动对偶综合工具中主要集成了求解最小不可满足子式的分支-限界算法与贪心遗传算法。自动对偶综合工具的基本流程是:以编码电路的RTL Verilog代码和工具的参数配置作为输入,首先采用Verilog语法分析器将设计转换为内部的中间表示,而后在状态空间中进行搜索,通过CNF产生器得到布尔公式,利用zCahff求解器判定公式的可满足性。若可满足,则继续搜索;否则采用不可满足子式求解器提取最小不可满足子式,并将该子式作为输入,反向抽取出解码电路的RTL代码。
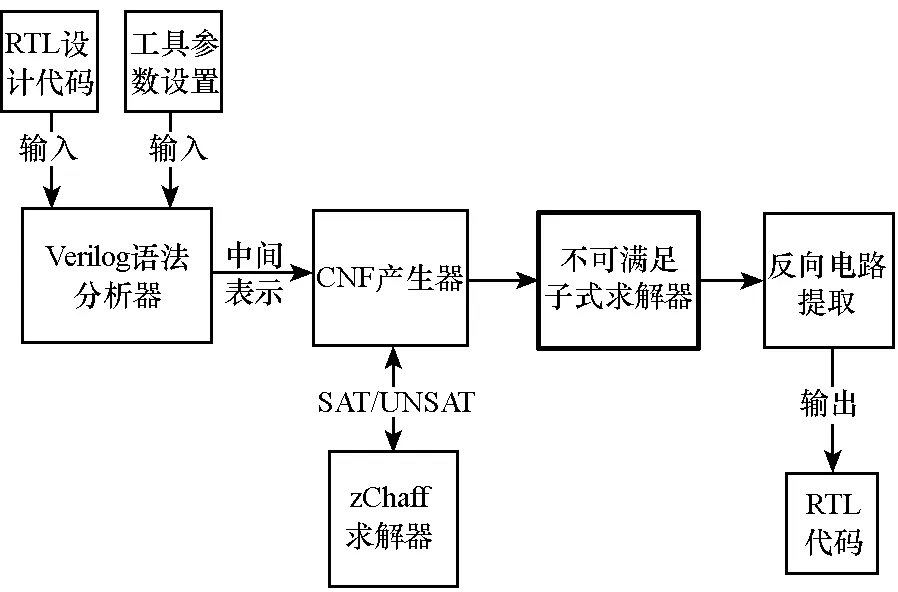
图2 自动对偶综合工具的结构Fig.2 Architecture of automatic decoder synthesis tool
4 实验结果对比与分析
为了验证不可满足子式求解算法在电路自动对偶综合中的作用,以业界普遍采用的、遵循IEEE802.3ae标准的编码器电路作为实例。IEEE802.3ae是IEEE于2002年发布的关于数据通信的IEEE802.3以太网协议与帧格式的一组协议规范,该标准定义了信号速率从1 Mb/s到1000 Mb/s的多种介质类型和技术。物理编码子层(Physical Coding Sublayer, PCS)是物理层实现的一个部件,PCS所使用的编码技术为8B/10B,该编码技术将报文编码为10位宽度的数据组,或者将10位的数据组解码为有效报文。
针对业界常用的PCS 8B/10B编码电路,当二元组
基于上述自动对偶综合工具产生的9个公式,分别采用分支-限界算法[2]以及贪心遗传算法[3]求解它们的最小不可满足子式。两种算法的运行时限都设置为1800 s。实验环境是主频为2.5 GHz的双核Athlon CPU,内存2 GB,操作系统为Linux的机器。
表1给出了分支-限界算法与贪心遗传算法在PCS编码电路上的结果。表中的第二列与第三列分别表示公式所包含的变元数与短句数;两算法下的第一、二、三列分别表示算法各自的运行时间、得到的最小不可满足子式长度以及单位时间移除的短句数。最后一列以百分比的形式表示最小不可满足子式所包含的短句数占公式总短句数的比例。
从表1可以看出,贪心遗传算法在运行时间方面优于分支-限界算法,只有分支-限界算法运行时间的52%~64%。另外,虽然贪心遗传算法仅得到了近似最小不可满足子式,但其只比分支-限界算法所求的最小不可满足子式多约4~8个短句。根据每秒剔除短句数nps的概念可得其计算公式是:nps= (NumLen)/Time,其中Num表示公式的短句数,Len表示不可满足子式的长度,即所包含的短句数,Time表示算法的运行时间,单位为秒。从nps列可以看出,贪心遗传算法每秒移除的短句数可以达到分支-限界算法的1.6~1.9倍。上述实验结果表明,贪心遗传算法虽然在求解最小不可满足子式的长度方面牺牲了一点精度,但在算法运行时间上取得了很大的优势,表明其同时兼顾算法效率与结果质量,且在单位时间内剔除的短句数要显著高于分支-限界算法,因此在众多的实际应用中,贪心遗传算法要比分支-限界算法更加高效、更加实用。

(a) DIMACS公式PCS_d1l1.cnf(部分)(a) PCS_d1l1.cnf in DIMACS format (part) (b) DIMACS公式PCS_d2l1.cnf(部分)(b) PCS_d2l1.cnf in DIMACS format (part)图3 DIMACS公式PCS_d1l1.cnf与PCS_d2l1.cnf (部分)Fig.3 PCS_d1l1.cnf and PCS_d2l1.cnf in DIMACS format (part)
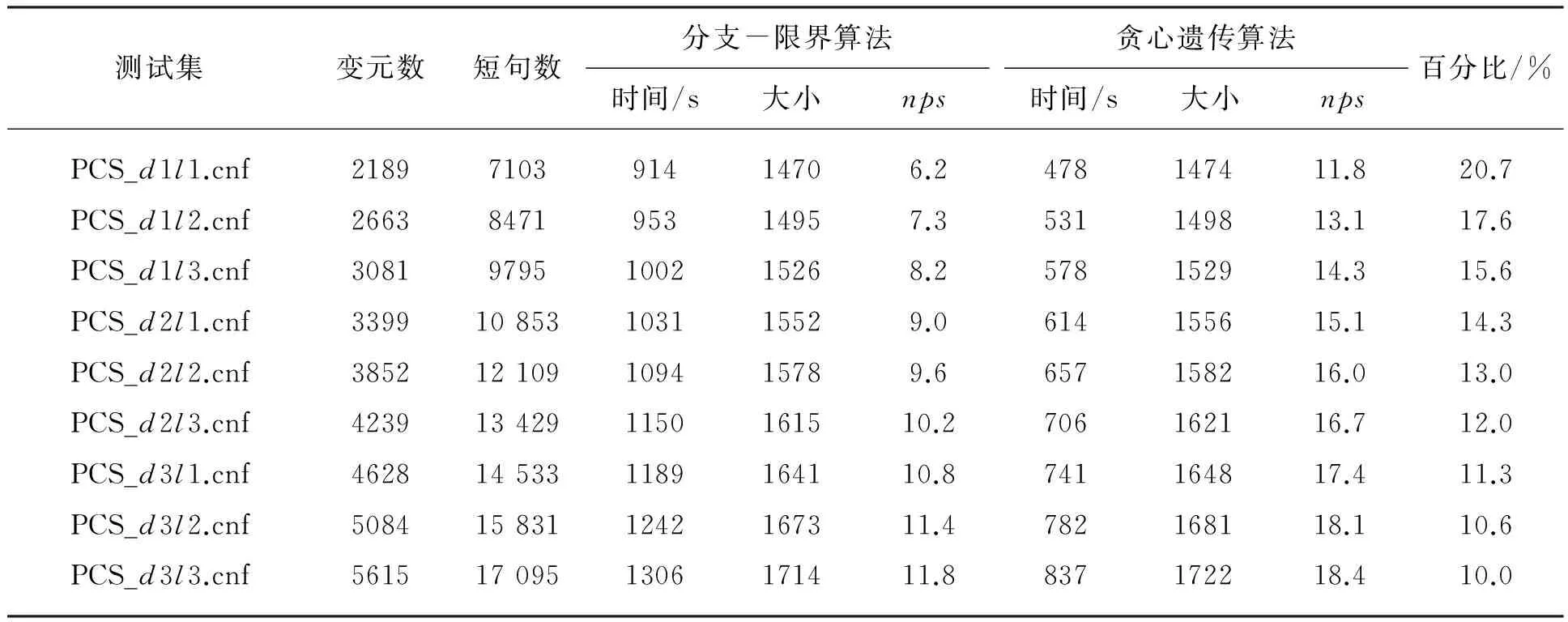
表1 分支-限界算法与贪心遗传算法的实验对比
从表1的最后一列可以看出,贪心遗传算法与分支-限界算法所求解的最小不可满足子式包含的短句非常少,仅占原始公式总短句数的10%~21%。这表明,在自动对偶综合工具中,通过求解最小不可满足子式能够大大简化状态空间,减小搜索范围,从而使得综合工具更加易于从编码电路中自动地提取PCS解码电路。通过实验说明,最小不可满足子式能够为诸如电路的自动综合等多种应用领域中的不可满足原因提供最精确的解释,最大限度地剔除无关因素,从而显著地加速应用的运行效率。
5 结论
解码电路的自动综合方法是不可满足子式的典型应用。由于不可满足子式越小,越能加速解码电路的提取,因此,将两种能够高效求解最小不可满足子式的算法——分支-限界算法与贪心遗传算法,集成到电路综合工具中。采用通信领域最典型的IEEE802.3ae标准编码电路作为测试集,将两种算法进行了对比实验。结果表明,在运行时间与每秒剔除的短句数方面,贪心遗传算法优于分支-限界算法。并且通过该实验表明,最小不可满足子式求解器能够显著地提高解码电路自动综合工具的效率。
References)
[1] Shen S Y, Qin Y, Wang K, et al. Synthesizing complementary circuits automatically[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2010, 29(8): 1191-1202.
[2] Liffiton M H, Mneimneh M N, Lynce I, et al. A branch and bound algorithm for extracting smallest minimal unsatisfiable formulas[J]. Constraints, 2009, 14(4): 415.
[3] 张建民, 沈胜宇, 李思昆. 最小布尔不可满足子式的求解算法[J]. 电子学报, 2009, 37(3): 993-999.
ZHANG Jianmin, SHEN Shengyu, LI Sikun. Algorithms for deriving minimum unsatisfiable boolean subformulae[J]. Acta Electronica Sinica, 2009, 37(3): 993-999. (in Chinese)
[4] Zhang L T, Malik S. Validating SAT solvers using an independent resolution-based checker: practical implementations and other applications[C] //Proceedings of Design, Automation and Test in Europe Conference(DATE′03), 2003: 10880-10885.
[5] Oh Y, Mneimneh M N, Andraus Z S, et al. AMUSE: a minimally-unsatisfiable subformula extractor[C] //Proceedings of the 41st Design Automation Conference(DAC′04), 2004: 518-523.
[6] Lynce I, Marques-Silva J. On computing minimum unsatisfiable cores[C] //Proceedings of the 7th International Conference on Theory and Applications of Satisfiability Testing(SAT′04), 2004: 305-310.
[7] Gershman R, Koifman M, Strichman O. Deriving small unsatisfiable cores with dominator[C] //Proceedings of the 18th International Conference on Computer Aided Verification(CAV′06), 2006: 109-122.
[8] Dershowitz N, Hanna Z, Nadel A. A scalable algorithm for minimal unsatisfiable core extraction[C] //Proceedings of the 9th International Conference on Theory and Applications of Satisfiability Testing(SAT′06), 2006: 36-41.
[9] van Maaren H, Wieringa S. Finding guaranteed MUSes fast[C] // Proceedings of 11th International Conference on Theory and Applications of Satisfiability Testing(SAT′08), 2008: 291-304.
[10] 陈振宇, 徐宝文, 周从华. 一种基于消解的变量极小不可满足子公式的提取方法[J]. 计算机研究与发展, 2008, 45(z1): 43-47.
CHEN Zhenyu, XU Baowen, ZHOU Conghua. A resolution-based approach for extracting variable minimal unsatisfiable sub-formulas[J]. Journal of Computer Research and Development, 2008, 45(z1): 43-47. (in Chinese)
[11] 赵相福, 欧阳丹彤. 使用SAT求解器产生所有极小冲突部件集[J]. 电子学报, 2009, 37 (4): 804-810.
ZHAO Xiangfu, OUYANG Dantong. Deriving all minimal conflict sets using satisfiability algorithms[J]. Acta Electronica Sinica, 2009, 37(4): 804-810. (in Chinese)
[12] Nadel A. Boosting minimal unsatisfiable core extraction[C] // Proceedings of the 10th International Conference on Formal Methods in Computer Aided Design (FMCAD′10), 2010: 221-229.
[13] Marques-Silva J, Lynce I. On improving MUS extraction algorithms[C] //Proceedings of the 14th International Conference on Theory and Applications of Satisfiability Testing(SAT′11), 2011: 159-173.
[14] Ryvchin V, Strichman O. Faster extraction of high-level minimal unsatisfiable cores[C] //Proceedings of the 14th International Conference on Theory and Applications of Satisfiability Testing(SAT′11), 2011: 174-187.
[15] Chen H, Marques-Silva J. Improvements to satisfiability-based boolean function bi-decomposition[C] //Proceedings of the 19th International Conference on VLSI and System-on-Chip (VLSI-SoC′11), 2011: 52-72.
[16] Belov A, Lynce I, Marques-Silva J. Towards efficient MUS extraction[J]. Journal AI Communications, 2012, 25(2): 97-116.
[17] Belov A, Janota M, Lynce I, et al. On computing minimal equivalent subformulas[C]// Proceedings of the 18th International Conference on Principles and Practice of Constraint Programming(CP′12), 2012: 158-174.
[18] Liffiton M H, Malik A. Enumerating infeasibility: finding multiple MUSes quickly[C]// Proceedings of the 10th International Conference on Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, 2013: 160-175.
[19] Nadel A, Ryvchin V, Strichman O. Efficient MUS extraction with resolution[C]// Proceedings of 13th International Conference Formal Methods in Computer Aided Design(FMCAD′13), 2013: 197-200.
[20] Lagniez J M, Biere A. Factoring out assumptions to speed up MUS extraction[C] //Proceedings of 16th International Conference on Theory and Applications of Satisfiability Testing(SAT′13), 2013: 276-292.
[21] Marques-Silva J, Janota M, Belov A. Minimal sets over monotone predicates in Boolean formulae[C] //Proceedings of the 25th International Conference on Computer Aided Verification(CAV′13), 2013: 592-607.
[22] Belov A, Heule M J H, Marques-Silva J. MUS extraction using clausal proofs[C] //Proceedings of 17th International Conference on Theory and Applications of Satisfiability Testing(SAT′14), 2014: 48-57.
[23] Marques-Silva J, Previti A. On computing preferred MUSes and MCSes[C] //Proceedings of 17th International Conference on Theory and Applications of Satisfiability Testing(SAT′14), 2014: 58-74.
Optimization method of decoding circuits′ synthesis using unsatisfiable subformulas
ZHANG Jianmin, LI Tiejun, MA Kefan, XIAO Liquan
(College of Computer, National University of Defense Technology, Changsha 410073, China)
Explaining the causes of unsatisfiability of the Boolean formulas has many real applications in various fields. The minimum unsatisfiable subformulas can provide most accurate explanations for the causes of infeasibility in many application fields such as the automatic circuits' synthesis. Therefore, two best algorithms of extracting the minimum unsatisfiable subformulas, respectively called the branch-and-bound algorithm and greedy genetic algorithm, were integrated into the automatic synthesis tool of decoding circuits. Adopting the standard encoding circuits in communication fields as the benchmarks, the study compared and analyzed the two algorithms. The experimental results show that the greedy genetic algorithm outperforms the branch-and-bound algorithm on runtime and removed clauses per second. The results also show that the unsatisfiable subformulas play an important role in the process of synthesizing automatically the decoding circuits.
circuit synthesis; formal method; satisfiability solving; unsatisfiable subformula
10.11887/j.cn.201605001
http://journal.nudt.edu.cn
2015-11-17
国家自然科学基金资助项目(61103083,61133007);国家重点研发计划资助项目(2016YFB0200203)
张建民(1979—),男,山西平遥人,副研究员,博士,Email: jmzhang@nudt.edu.cn
TP391
A
1001-2486(2016)05-001-06
