基于小波变换的改进LMS自适应算法在射电天文数字终端的应用∗

李浩然，陈卯蒸，裴鑫

(1.中国科学院新疆天文台，新疆乌鲁木齐830011；2.中国科学院大学，北京100049)

随着国内乡村城镇的扩张以及人口流动影响，原本台址环境良好的望远镜也遭受着无线电干扰．目前，射频干扰(RFI)已经成为射电天文观测的主要问题．我们应当采取相应措施来解决射频干扰问题，消除射频干扰的主要手段包括：调整观测时间，避开射频干扰高峰时期射电干扰屏蔽，停止周边周期性辐射爆发的仪器接收机数字终端滤波．前两种手段只能被动地规避干扰影响，不仅降低了观测的效率，无形中也增加了运行成本．然而，数字终端滤波手段得利于处理速度快、动态范围高、处理噪声能力强等优点，逐渐成为抑制射频干扰的主要手段．

目前，射电天文领域采取的数字滤波技术以LMS算法为主.美国国家射电天文台绿岸望远镜采用的LMS算法[1]，虽然有效地抑制了干扰，可是由于LMS算法的局限性，不能达到较高的计算精度与收敛速度．荷兰韦斯特伯格综合孔径望远镜采用了改进LMS算法[2]，在系数更新机制方面进行了创新，采用2个小天线输入信号的均值作为参考输入，但是由于干扰噪声的宽频带，导致滤波器效果不稳定．澳大利亚国家天文台帕克斯望远镜采用NLMS算法[3]，虽然改善了滤波效果，但是因为选用了固定的步长，导致运算复杂度增加、跟踪性能变差．

本文针对L波段脉冲星信号的特点，结合小波滤波与自适应滤波的优点，提出了一种基于小波变换的改进LMS算法，用于射电天文数字终端去除噪声．

1 小波分解

1.1 小波分解原理

1988年Mallat把计算机视觉领域内的多分辨率分析方法与小波分析方法结合，提出了小波分解的快速算法—Mallat塔式算法．该算法是一种多尺度分析算法．随着尺度从大到小的变换，在不同的尺度上可以从粗到细观察出信号的不同特征．在大尺度时，可以观察出信号的包络；在小尺度时，可以观察出信号的细节．

多尺度分析算法是将原信号S在2个正交子空间进行逐级分解，每次输入都将分解成高频细节分量和低频近似分量，输出采样频率减半，解释该过程的方程式为

其中,cj是第j级的近似分量，dj是第j级的细节分量．

假设原始信号的频率范围是[0∼fs],每进行一次分解，相当于近似分量分别经过一次低通滤波器和一次高通滤波器．那么，第一次分解得到的结果：近似分量c1的频率范围为[0∼fs/2]、细节分量d1的频率范围为[fs/2∼fs]．第二次分解是针对第一次输出的近似分量进行分解，其结果为：近似分量c2的频率范围为[0∼fs/4]、细节分量dj的频率范围为[fs/2j∼fa/2j−1]．

所以，数字信号的二进制小波变换相当于经过一组数字带通滤波器，第j级的细节分量相当于带通滤波器的频带范围是[fs/2j∼fa/2j−1]．当然，选用不同的小波基，会导致频率响应不同．

1.2 小波基函数和阶数的选定

由于脉冲星信号具有短而稳定的脉冲周期的特点，所以选择小波基函数时，选用可以进行连续小波变换的小波基；在脉冲星观测时，经常出现窄带噪声干扰，在进行终端滤波时，应当检测并消除奇异点，所以应当选用具有正交性的小波基；在脉冲星观测时，应当注意到噪声干扰呈现频段范围宽、幅值变化大的特点，不利于自适应滤波器系数的收敛，应当选用具有时域紧支性的小波基函数．所以，我们选择Daubechies(简称db小波)作为小波基函数．它具有较强的分频能力，小波的阶数越高，分频能力越强，但是对应的计算也越复杂．针对实测脉冲星信号，选用不同的阶数进行测试，根据信号和噪声的小波系数在不同尺度上的差异性，来判断适合脉冲星信号小波分解的阶数．

我们使用观测到的J1141-6545脉冲星信号，选用db小波基函数，在1∼5阶尺度上进行分解，分解图如图1所示．其中，e是脉冲星信号，di是第i阶的低频近似分量，ai是第i阶的高频细节分量．由分解图可知，d5相对于d4变化没有之前2次分解那么明显，a5相对于a4更平滑，会导致自适应滤波之后信号失真程度偏大，故最适合脉冲星信号db小波分解的阶数为4阶．

2 基于小波变换的自适应滤波器

2.1 小波自适应滤波器

按照Mallat算法将脉冲信号x(n)分解之后，依据经验区分信号与噪声．目前去噪的方法主要有：利用小波变换模极大值原理去噪、利用小波阈值去噪、利用小波系数相关性去噪．当信号与噪声有重叠频谱时，这些方法虽然能实现信噪分离，提高信噪比，但并不能实现噪声信号的最佳估计．因此，难以实现最佳滤波．但小波变换所分离的噪声信号一定与原噪声成分相关，这为实现自适应滤波提供了可能，其自适应模型如下所述．

图1 脉冲星信号使用db小波基函数的5阶小波分解图

假设输入的脉冲星信号x(n)=s(n)+n(n)，其中s(n)是有用信号，n(n)是噪声信号，如图2所示．脉冲星信号x(n)经过基于4阶db小波基函数的小波分解，得到4个通道的噪声分量d1∼d4，将4个噪声分量依次延迟1个单位，分别作为自适应滤波器的抽头输入，与经过多次迭代的最优权值系数w相乘累加之后的结果为提取出来的噪声信号e(n)，让脉冲信号x(n)与e(n)相减，得到去噪的信号y(n)．

对应的计算公式，如下：

图2 基于小波变换的自适应滤波器的结构框图

其中，x(n)经过小波分解后的4阶噪声分量构成噪声信号集S=[s1,s2,s3,s4]，经过依次延迟后作为公式（3）的输入信号集．

公式（3）中si(n)是参考信号，e(n)是经过改进算法处理后的参考信号，wi(n)由权值更新机制决定的一次自适应系数．每进行一次计算，参考信号与系数相乘得到新的e(n)值．经过多次循环计算之后，当e(n)与脉冲星信号x(n)中的干扰噪声信号相等时，将会得到没有受干扰噪声影响的脉冲星信号，同时得到维纳-辛钦方程的最优解．

公式（4）中，x(n)是脉冲星信号，y(n)是反馈的误差信号．在每一次循环计算中，脉冲星信号与e(n)相减，得到的反馈误差重新进入到权值更新机制里，代入到下一轮的权值更新．

公式（5）中，w(n+1)是更新后的权值系数，w(n+1)是旧的权值系数．误差信号与参考信号做一次计算，得到权值系数的变化值w(n)．

2.2 改进的权系数更新机制

文献[6]采用的是传统LMS自适应算法，使用最速下降算法作为权系数更新方式，其核心思想是用平方误差来替代均方误差．该方法是沿最速下降方向(负梯度方向)连续调整权向量w，其公式如下：

文献[7]采用的是Widrow-Hoff LMS自适应算法,采用随机梯度法来求解最佳权系数，该算法用瞬时“−2y(k)∗x(k)”来替代“−2E[e(n)∗x(n)]”的估计运算．其权值更新表达式为：

由于LMS算法使用上一个时刻的抽头参量作为该时刻的均方误差最小的依据，而没有使用本时刻的抽头参量对过往的数据块做重新估计后的累积平方误差最小作为依据，导致LMS算法对非平稳信号的适应性差．

针对脉冲星信号的非平稳性，改进算法用反馈误差在本时刻之前(包括本时刻)的算数平均值作为本时刻反馈系数代入到权值更新机制内，即用反馈系数的均值代替T时刻的反馈系数YT，这使得每个时刻对所有已输入信号重估的平方误差的加权和最小．

由于参考信号具有噪声相关而与信号无关的特性，所以我们采用相关算法，对脉冲星信号中的噪声干扰进行消除．

这种算法可以更全面地消除脉冲星信号中的干扰噪声，因为相关算法相对最速下降算法在分析信号的边缘方面具有优势，在信号与噪声重叠程度较大的条件下，能最大程度地完成信噪分离和提高信噪比．

2.3 改进的步长算法

自适应滤波算法有3个重要指标：计算量、收敛速度及稳态失调．可以通过减少固定步长µ来减少自适应滤波算法的稳态失调,提高算法的收敛精度，但是会导致算法的收敛速度和跟踪能力的下降．

文献[8]利用小波的分频特性，先将信号分解到不同的频段上，然后对各个频段信号使用固定步长的自适应滤波，其针对单一频率的干扰，采取大量仿真的方法得到最优的参数．

在进行相对简单的信号去噪时,使用固定步长就已足够．但是针对脉冲星信号进行噪声干扰去除的时候，固定步长不能达到较好的滤波效果,需采用变步长的策略．

常用的变步长算法是Sigmod函数变步长最小均方算法．该算法针对具体的含噪信号,通过选择合适的隶属度函数,从而推导出步长因子µ和反馈误差e(n)之间的非线性函数关系,以任意精度逼近µ与e(n)的连续函数．Sigmod函数方程式：

其中，γ调节µ的最大值，α调节曲线的倾斜度，β调节µ的最小值．

µ(n)与e(n)的关系曲线，如图3.

图3 步长u(n)与反馈误差e(n)之间的Sigmod函数关系

在固定步长中，使得LMS算法收敛的条件是0<µ<γmax,γmax是脉冲星信号自相关矩阵的最大特征值，所以在改进算法中，γ<1<γmax可以保证算法一定收敛，即取0.2.在γ选定的情况下，将1线与2线进行对比，1线的最小值明显大于0．不满足误差e(n)为0时，步长µ(n)也为0的条件．所以，影响最小值的因子β=100较为合适．

在γ与β选定的情况下，将2线、3线、4线同时进行对比．为了保证在初始阶段或未知系统参数发生变化时，步长应该较大，以便有较快的收敛速度和对时变系统的跟踪速度．2线的初始步长0.2优于3线的初始步长0.12.而在算法收敛后，不管主输入端干扰信号多大，都应保持很小的调整步长以达到很小的稳态失调噪声．2线相对于4线更能满足这样的变化要求，并且在整体的变化趋势中，2线在收敛中期较大的收敛倾斜度，也使其收敛速度优于3线．经过多次试验，我们选定γ=0.2β=100α=10作为Sigmod函数的参数值．

针对这类脉冲星信号选用的Sigmod函数是：

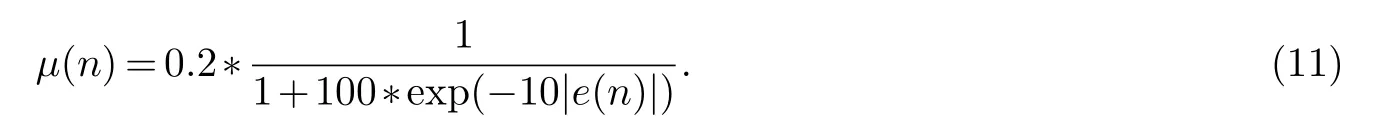
3 改进算法的性能分析

我们采用观测基地的脉冲星观测数据作为输入信号．选用的脉冲星为J1141-6545．该信号是时域信号，纵坐标表示的是流量，范围在0Jy∼0.01Jy之间，横坐标表示的是相位，范围在0∼1之间，拥有1 000个采样点．原始信号具有较厚的噪底，从图中能辨别出1个波峰．噪声和干扰在信号的两侧分布．

我们采用1个实验组和2个对比组的实验方法来分析小波自适应滤波器的性能特点．图4中的第2幅图，采用固定步长的LMS算法对脉冲星信号进行处理，步长选定为0.2,抽头阶数选定为4阶．图4中的第3幅图，利用小波的能量集中特性，采用阈值滤波算法对脉冲星信号进行处理．图4中的第4幅图，采用本文改进的小波自适应滤波算法进行处理．

图4 脉冲星信号经过3种算法滤波处理之后的结果

图5 天体测量信号经过3种算法滤波处理之后的结果

由图中可以看出，改进算法相对于小波滤波和自适应滤波，达到更好的滤除效果．自适应滤波因为采用了本时刻反馈误差，没有考虑到之前时刻的累积误差影响，导致整个波形都成锯齿形，影响了信号质量．而采用改进权值更新机制的小波自适应算法很好地克服了这一缺点．小波滤波相对于自适应滤波，滤波效果更好，但是其滤波效果没有小波自适应算法好，仍然有少量的噪声残留．改进的小波自适应算法集成了前两种算法的优点，是三种算法中滤波效果最好的．算法的效果对比如表1.

为了验证算法的普适性，我们采用南山观测基地的天体测量信号．信号是时域信号，纵坐标是功率，其范围是164 000µW∼166 500µW；横坐标是采样点数，拥有1 024个采样点．从图中大致可以分辨出3个波峰，剩余的波峰可能存在于干扰噪声中．

经过本文改进算法处理的信号，去除的噪声足够多，能够清晰分辨出第4个脉冲信号．相应的算法效果对比见表2.

表1 3种算法的滤波效果对比

表2 3种算法的滤波效果对比

图6 双脉冲星信号经过3种算法滤波处理之后的结果

我们发现在使用其他类型的脉冲信号时，改进的小波自适应算法相对于前两种算法依然保持着优势．

为了进一步验证该算法对脉冲星观测信号质量的提高．我们采用Parkes的双脉冲星信号进行验证．采用的射电源是J0737-3039A．

经过改进算法处理的双脉冲星信号，脉冲信号轮廓已经可以辨识出来，有助于科学家们进一步分析脉冲星的特性．

4 结论

本文以新疆天文台南山25m天线系统改造计划为研究背景，以数字终端噪声干扰消除作为目标，分析比较了多种噪声干扰消除算法的优缺点，提出了改进的小波自适应算法进行滤波处理，得到理想的滤波效果．下一步，会把温度、湿度、风速等影响因子考虑进去，解决由这些因素造成的信号形变．为获取更优质的脉冲星观测信号做进一步的研究．