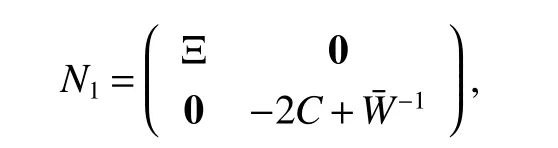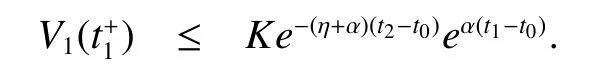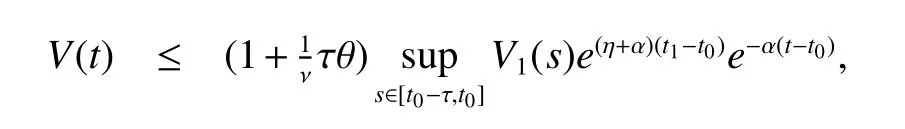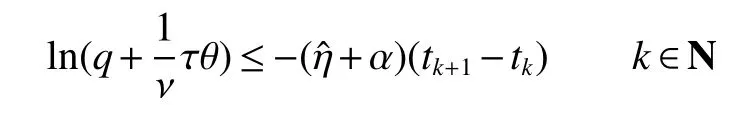Synchronization of Competitive Neural Networks with Time-varying Delays and Impulses Effects∗
2016-11-28MEIXuehuiZHANGLiweiYUZhiyongJIANGHaijun
MEI Xuehui,ZHANG Liwei,YU Zhiyong,JIANG Haijun†
(1.College of Mathematics Sciences,Dalian University of Technology,Dalian Liaoning 116024,China;2.College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract: In this paper,the issue of synchronization of the competitive neural networks(CNNs)with time-varying delays is investigated via impulses control.Based on Lyapunov-Krasovski function method and the matrix inequality theory,a linear matrix inequality(LMI)criterion is presented for achieving synchronization of the CNNs.Besides,an algebraic form sufficient criterion,which reflects the relation among the time delays,impulses feedback matrices,and impulsive interval,is proposed to guarantee exponentially synchronization of the CNNs with bounded time-varying delays.
Key words:competitive neural networks;synchronization;time-varying delays;impulses
0 Introduction
The biological neural networks exist a phenomenon of the collateral inhibition.This kind of inhibition will lead to competitive action between neuronal cells.At the beginning,each neuron has the same opportunities in response to the system input,but they have the different level of excitement.In generally,the strongest neuron in exciting have the strongest inhibitory effects on the peripheral neurons.At the same time,the excitation of other neurons is to get the maximum inhibition.Therefore,both slow and fast dynamic phenomena occurs in separate time scales on a wide class of neural networks.Competitive neural networks(CNNs)model just describes this phenomena and is one of the important classes of neural networks with unsupervised synaptic modifications.In 1983,Cohen and Grossberg[1]firstly proposed the CNNs.Then there are a lot of literatures about the CNNs[2−9].As for the basic form of the CNNs,there are two types of state variables in it:the short-term memory(STM)variable which describe the fast neural activities and the long-term memory(LTM)variable which describe the slow unsupervised synaptic modifications.Based on the above description,the CNNs basic model is given as followswhereNis the number of the STM states,Pis the number of the constant external stimulus;xidenotes the neuron current activity level,fi(·)denotes the output of neurons,mij(t)is the synaptic efficiency, σjis the constant external stimulus;ai>0 is the time constant of the neuron;ci>0 is disposable scaling constant;dikdenotes the connection weight of delayed feedback between theith neuron and thekth neuron;bidenotes the strength of the external stimulus,ε>0 denotes the time scale of STM states.

Specially,in nature,synchronization is a typical collective behavior due to its underlying applications in biological evolutions,chemical reactions,secure communications,and so on.Since the pioneering work of Pecora and Carroll[10],the problem of synchronization has received much more interests[4,5,8,13−16].On the other side,the CNNs with different time scales are extended in Amari’s model for primitive neuronal competition[11]and Grossberg’s shunting networks[12].In fact,there exist time delays both the real neural systems and the circuit implementations of neural network models due to signal transmission between finite switch speed or neurons.Therefore,the effect of time delays should be considered in the investigation of synchronization.In the last few decades,lots of results about the synchronization and the stability of the CNNs with time delays have been obtained[2−9].
In addition,it is well known that the rapid changing will appear in some stage of the development in many practical problems.As a matter of convenience,in the process of mathematical simulation,we always assume that the process is done through the instantaneous changing.The phenomenon is called as impulse.The impulse is widespread in field of modern science and technology,and has been paid much attention due to its important applications in many areas,such as aerospace science,information science,communications,control system,medicines,economy fields and so on.It is noticeable that the time delays and impulses might give rise to unstable factors during its derived process.In the past few years,many researchers have investigated the synchronization and impulsive control of various kinds of neural networks[13−16].
However,all of the above-mentioned works have not considered the synchronization of the competitive neural networks with time-varying delays and impulses.Motivated by the discussions,in this paper,we investigate the synchronization problem of the competitive neural networks with time-varying delays and impulses.Some sufficient conditions are established and a example with simulations is presented to demonstrate the effectiveness of our results and feasibility of the schemes proposed.Obviously,it is beneficial to study this kind of synchronization problem in order to fill the research gap discussion above.
1 Preliminaries and Model formulation
For convenience,some notations are given in this section.ATandA−1represent the transposition and inversion ofA.A≥ 0(>0)represents the semi-positive(positive)and symmetrical matrix. λmax(A)and λmin(A)denote the maximal and minimal eigenvalues of a real symmetric matrixA.I(0)denotes an identity(zero)matrix with appropriate dimension. · represents the Euclidean norm of a square matrix or a vector.The symbol∗represens the elements below the main diagonal of a symmetric matrix.
Consider the following competitive neural networks with time-varying delays

where τ(t)is the time-varying delay;denotes the synaptic weight of delayed feedback between theith neuron and thekth neuron.
Settingsi(t)where σ =(σ1,σ2,...,σP)T,mi(t)=(mi1(t),mi2(t),...,miP(t))T,the system(1)can be formulated as follows

where|σ|2=++...+is a constant.Without loss of generality,the input stimulus vector σ is alluded to be normalized with unit magnitude|σ|2=1,then the CNNs(2)is simplified to
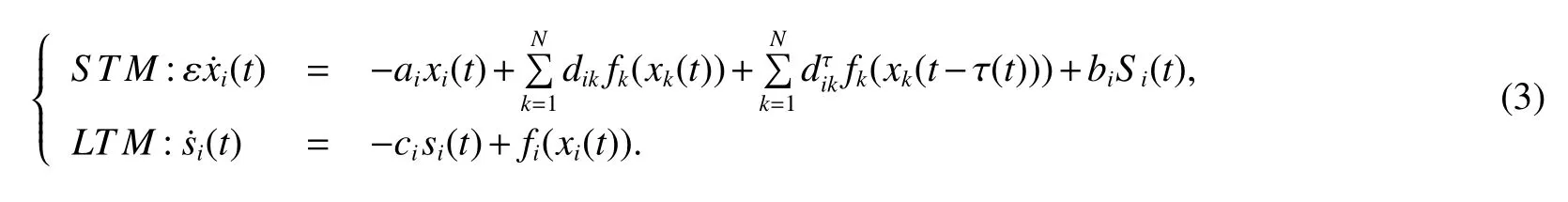
We rewrite the system(3)to a matrix formulation

wheret∈ R+=[0,+∞),x(t)=(x1(t),x2(t),...,xN(t))T,S(t)=(s1(t),s2(t),...,sN(t))T,A=diag(a1,a2,...,aN),D=(dik)N×N,Dτ=()N×N,B=diag(b1,b2,...,bN),C=diag(c1,c2,...,cN),f(x(t))=(f1(x1(t)),f2(x2(t)),...,fN(xN(t)))T,f(x(t−τ(t)))=(f1(x1(t−τ(t))),f2(x2(t−τ(t))),...,fN(xN(t−τ(t))))T.
The main aim of this paper is to achieve synchronization between the master system(4)and the following slaver system(5)by designing suitable impulsive controllersui(t),i=1,2.Thus,the slaver system can be written as

whereu1(t)andu2(t)are the control input.Define the synchronization error states ase(t)=y(t)−x(t)andz(t)=R(t)−S(t),thenu1(t)andu2(t)are designed as the following form

whereQi∈RN×N,(i=1,2)is the feedback controller gain matrix to be determined latter.
The dynamical networks of the error systems are given as follows

whereg(e(t))=f(y(t))−f(x(t)),g(e(t−τ(t)))=f(y(t−τ(t)))−f(x(t−τ(t))).
In order to get the main results,the following assumptions are presented
(A1) There exist some positive constantsli>0(i=1,2,...,N),such that the output functionsfisatisfy the following conditions

wherexi(t),yi(t)∈R.
(A2)Let time-varying delay τ(t)be positive real valued continuous function and its derivation˙τ(t)satisfies

(A3) Time-varying transmission delay satisfies 0<τ(t)≤τ,where τ is constant real number.
Definition 1[9]The master system(4)and the slaver system(5)is synchronized if

Lemma 1[17]For any given real matricesX,Y,Gof appropriate dimensions satisfying 0

2 Main Results
In this section,some synchronization criteria for competitive neural networks with impulses are established.
Theorem 1 Suppose that(A1)and(A2)hold.There exists a symmetric and positive definite matrixW,such that

whereL=diag(l1,l2,...,ln).And λmax((I−Qi)T(I−Qi))≤1 holds.Then,the master system(4)and the slaver system(5)are synchronized completely by the impulsive controller(6).
Proof Construct firstly the Lyapunov functional

where ψ−1(s)is the inverse function of ψ(s)=s−τ(s).The purpose is to prove˙V(t)<0,fort∈(tk−1,tk)andV(t+k) First,whent∈ (tk−1,tk),one has Combination with(A1)and Lemma 1,the following inequality is obtained where According to(8),˙V(t)<0 fort∈(tk−1,tk). Secondly,whent=tk,one has This ends the proof. Remark 1 It is well known that the impulse is important for the stability of system.A stable system may becomes unstable if the system suffers strong impulse.The impulse also can make an unstable system achieving stable.Hence,how to design an appropriate impulse feedback matrix is very essential for the stability of system.In Theorem 1,the synchronization conditions of the master system(4)and the slaver system(5)are given.According to analysis of Theorem 1,condition(8)holds for system without impulse control,this means that the error systems(7)is stable if the systems without impulse control.However,in order to keep the stability the of the system under the impulse,the feasible region of the impulse feedback matrixQi(i=1,2)is provided. The following step,we will derive sufficient condition for the exponential synchronization of the master system(4)and the slaver system(5). Theorem 2 Suppose that assumptions(A1),(A2)and(A3)hold,α>0 and τ≤tk−tk−1for allk∈N.Moreover,if there exist positive symmetric matricesW,¯Wand a positive constant η such that (5)are exponentially synchronized via impulsive controllers(6). ProofConsider the following Lyapunov functional Whenttk,by Lemma 1,the termeT(t)(+2L)z(t)satisfeis By Theorem 1 and(12),one has where α = λmax(N1)>0 and where and From above deriving procedure,we get the following inequalities For obtaining our conclusion in Theorem 2,let and The following inequality is to be claim that for allk∈N is true. Now,let us give the mathematical induction. Fort∈[t0,t1],it can be obtained from(13)that Combination with(14)and(17),one implies that And by(15),it also has where θ=λmax(LWL).Thus,from(17),(18)and(19),it follows that Then,fort∈(t1,t2],one knows that i.e fork=2,(16)holds. Next step,suppose(16)to be satisfied fork=p(p>2),that is,fort∈ (tp−1,tp], It must show that(16)holds fork=p+1. From(18)and(19),one concludes then,by(20)fork=p+1,that ist∈(tp,tp+1] which implies that(16)holds for allk∈N.Final step,we will derive convergence estimation.The following formulation is easy to observe From(16),fort∈ (tp−1,tp],one has that is where τ≤t1−t0,and fort≥t0,Therefore,whent→+∞,one hase(t)+z(t) →0.This proof is complete. Remark 2 From the Theorem 2,the system(4)and the system(5)are the exponential synchronization as long as the selected constant η satisfeis condition(11).It can be see that the synchronization rate of the system(7)is−. In system 7,if time delay τ(t)=0,vector functiong(e(t−τ(t)))can be incorporated intog(e(t)).Then the following result can be easily obtained. Corollary 1 Suppose that(A1)holds,>0,andtk+1−tk>0,for allk∈N.Moveover,if there exist positive symmetric matricesW,and a positive constantñ such that Remark 3 Note that the synchronization of competitive neural networks without time delays via impulses control is a special case of system(4).The analysis is roughly similar to Theorem 2.In the case without time delays,one only need to choose the Lyapunov functionV(t)=V1(t),and the synchronization rate of the system(7)is− Remark 4 From above discussion,it is noted that the synchronization of competitive neural networks with invariable time delays via impulses control is another special case of system(4).Meanwhile,the derivation processes are also similar to Theorem 1 and Theorem 2.One also just only need to replace τ(t)by τ,where τ is a small scale. In system(5),if choosing the impulsive controller gainswe have the following corollary. Corollary 2 Suppose that(A1),(A2)and(A3)hold,α>0,andtk+1−tk≥τ,for allk∈N.Moveover,if there exist positive symmetric matricesW,and a positive constantñ such that where α = λmax(N1),θ= λmax(LWL),q=max(1−),∈(0,2),i=1,2,j=1,...,N,N1=Then the master system(4)and the slaver system(5)are exponentially synchronization via impulsive controllers(6).