Quantum Phase Diagram of the Third-filled t-U-V-J Model in One Dimension∗
2016-11-28AsharErshatDINGHanqinZHANGJun
Ashar Ershat,DING Hanqin,ZHANG Jun
(College of Physical Science and Technology,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract: We investigate a one-dimensional third-filled electron system with on-site,nearest-neighbor-site Coulomb and exchange interactions at weak coupling.The bosonozation and renormalaliztion group analysis predict occurrence of quantum transitions.The calculation of relevant correlation functions determines dominant phases.The ground state phase diagram consists of the charge-density wave(CDW),spin-density-wave(SDW),triplet-superconductivity(TS)and singlet-superconductivity(SS)phases.The results are expected to provide an important insight into 1D extended Hubbard models.
Key words:t-U-V-J model;phase diagram;weak coupling;bosonization
0 Introduction
During the past decades,the one-dimensional(1D)correlated electron systems have been extensively studied as an important model,motivated not only by theoretical interest but also by the discovery of quasi-1D conductors and high-Tcsuperconductivity[1−4].The 1D Hubbard model is argued to be the archetype of strongly correlated electronic systems,describing itinerant electrons in a tight-binding chain with the hopping energytand the on-site repulsionU[5].The corresponding low-energy excitations are exactly charge-spin separable.At half filling,the charge excitation has a finite gap while the spin sector is gapless.Hence the ground state exhibits a Mott insulator characterized by a critical spin-density-wave(SDW).However,longer range interactions are needed to describe many effects observed in real materials.The conventional extended Hubbard model with an nearest-neighbor interaction of strengthV,is the simplest extension that gives rise to more complicated dynamics.As one of the basic many-body Hamiltonian in 1D,thet-U-Vmodel has been the subject of a large of studies[6−18].In the atomic limit,the correlations driven byUandVare explicitly frustrated.At half filling,the system is a charge-density-wave(CDW)insulator with fully gapped excitations for largeVand a SDW insulator with semi-gapped excitations for largeU.Such a common viewpoint had not been changed until Nakamura first pointed out that a bond-charge-density-wave(BOW)phase exists close to theU2Vlocation in between the SDW and CDW phases for small to intermediate values ofUandV[9].Thisexciting claim has further attracted increased interest in thet-U-Vmodel[10−17],by which the BOW state was intensively studied.The other well-known extension is thet-U-Jmodel including a nearest-neighbor spin exchangeJin stead ofV.This model has been intensively studied in the context of high-Tcsuperconductivity[18−21],especially the discovery of a new oxide-superconductor Sr2RuO4[22].At the same time,the phase diagram of thet-U-Jmodel was studied at half filling[23,24].
The two extensions describe the rich physics individually,but in certain case the charge and spin interactions between the inter-site electrons both play an important role.In order to describe the competing physics,one constructs the 1Dt-U-V-Jmodel,which incorporates bothVandJ.The Hamiltonian resds

where the symbolj,ldenotes the summation over neighboring sites.(c j,α)is the creation(annihilation)operator for an electron at sitejwith spin label α =↑,↓.nj,α=is the density operator for spin α at thej-th lattice site.The parameterst,U,VandJare all standard.At half fliling,the model Hamiltonian(1)was intensively studied.For example,by using the level spectroscopy method and bosonization theory,Huanget alinvestigated evolution of the BOW phase in 1D Mott insulators[25].Ding and Wang further reinforced the emergency of bond-located phases,pointing out that the BOW phase is realized forJ>0,but that a Haldane insulator(BSDW)is realized forJ<0[26].
As is known,the 1D repulsive interacting Fermi gas shows insulator behavior at half fliling due to relevant umklapp processes[1,2],whereas out of half fliling,the system may be conducting when the umklapp processes become irrelevant.At or out of half fliling,the system may possess a superconducting ground state for attractive interactions.Nevertheless,the generic feature of the 1D system described by the model Hamiltonian(1)has not fully understood away from half fliling and for attractive interactions(U,V<0).This paper will discuss such an issue.We consider the third-fliling(ν=1/3),and theJterm is only restricted to antiferromagnetic exchange(J>0)while the interactionsUandVare permitted to take positive or negative values.We also focus on weak-coupling case,where the bosonization and renormalization-group(RG)techniques may effectively work.As will be shown,the ground state may be insulating or conducting.The phase diagram contains four different sectors,characterized by the triplet-superconductivity(TS),singlet-superconductivity(SS),SDW and CDW phases.We have not found the bond-located phases,BOW and BSDW.The result is expected to provide an insignifciant insight into 1D correlated electron systems and extensions of the Hubbard model.
1 The analysis of low-energy field theory
The low-energy field theory is a weak coupling approach,assuming that the interactions are small in comparison with the Fermi level.In one dimension,the non-interacting dispersion relation is linearized around the left and right Fermi points,passing to the continuum limit through the replacement

wherex=ja,withabeing the original lattice spacing.The Fermi wave numberkF= νπ/2a,with ν electron density.Lα(x)andRα(x)respectively represent left and right moving component of the fermions,which are supposed to be slowly varying over distances of the order ofa.
The physics behind the extended Hubbard model becomes more transparent when it is described by the boson language.Bosonization is an effective technique to handle interacting one-dimensional fermionic systems[1,2,27].Behind that treatment,some of the interacting terms in the fermionic Hamiltonian become noninteracting in the bosonic Hamiltonian,and the remaining terms involve generally cosines of the bosonic fields.The boson representation of the left and right fermion operators are defined by a pair of dual boson fields φα(x)and θα(x)[28,29],

Applying the bosonization scheme and defining the charge(ρ)and spin(σ)fields φρ/σ=(φ↑±φ↓)/2 and θρ/σ=(θ↑±θ↓)/2,the low-energy behavior of the model(1)is then reformulated by the bosonized Hamiltonian,H=Hρ+Hσ+Hρσ.Out of the half filling,the charge part describes the Luttinger liquid process,and the componentHρcharacterizes the Gaussian mode,

The componentsHρandHρσdescribe the non-Luttinger liquid processes.Among others,the spin partHρcorresponds to the sine-Gordon mode,

TheHρσterm denotes the charge-spin coupling process,
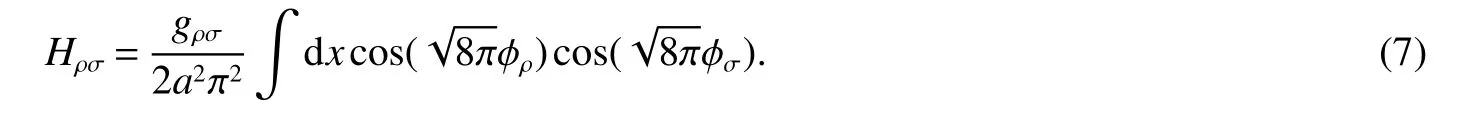
The RG argument claims that the energy scale ofHρσis larger than those of others.Therefore,we suppose that the operatorgρσis irrelevant in the weak-coupling regime,so theHρσpart can be safely omitted.
Above,the Fermi velocityvF=2tasin(kFa).The parametersKρandKσare Gaussian couplings of the charge and spin elementary excitations,respectively.The couplinggσrepresents the backward scattering.At third filling,they are given by

Once the charge-spin separation occurs,we can easily analyze the low-energy excitations by the perturbative RG method.If the coefficient of a cosine decreases in the RG flow,the fixed point corresponds to a trivial theory of free bosons.Whereas,if the RG flow scales to strong fixed points,the coefficient of a cosine increases.In this case,the fields are trapped in a minimum of the energy and the different phases can be characterized by calculating the expectation value at this minimum of the bosonic operators.To be specific,in the spin channel the relevant importance of the backward process is obtained in terms of the one-loop RG equations,which are derived by the change of the cutoffa→aedy,
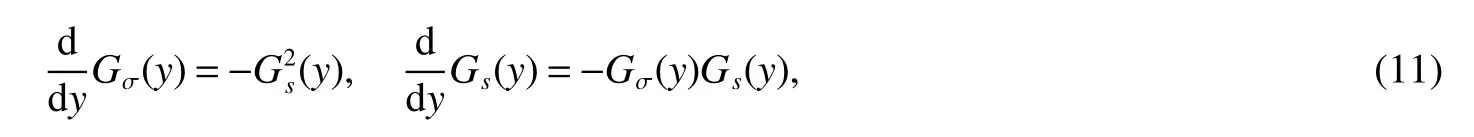
whereGσ=2(Kσ−1)andGs=gs(y)/πvF.Due to spin SU(2)symmetry,the Gaussian fixed lineGs=0 is stable forgs≥0 and becomes unstable forgs<0.In other words,for repulsive backward scattering,the Gaussian parameter is renormalized asK∗σ=1,and the spin channel is massless;For attractive backward scattering,K∗σ=0,and the spin channel is massive,accompanied by the average value φσ=0.Consequently,the spin-gap transition occurs at

separating a spin-gapped phase forU
Unlike the spin mode,the RG argument cannot applied to the charge excitation because of the collapse of umklapp process.In this situation,Kρis not renormalized,and we can calculate the value ofKρ[30].The system is a superconductor forKρ>1 while is an insulator forKρ<1.Thus,the superconductor-insulator transition correspond to

The insulating phases are dominant forU>Uρ,and at zero temperature the superconducting phases are favorable forU In this section,we discuss the properties of dominant phases.Of interest is the 2kF-CDW and SDW correlations for the insulating phase,and the TS and SS Cooper-pairing types for the superconducting phase.To this end,we introduce the non-half filled(ν 1)order parameters defined on sites: They describe the correlation functions,which decay as power laws without logarithmic corrections[8] with exponents αi Table 1 The different types of dominant phases,depending on the presence of a charge/spin gap ∆ρ/σ and on the behavior of the related field φρ/σ,which can either be fluctuating or pinned around the specified values The different pinning values for the field φρ/σin Table 1 determine the order parameters for the gapped phases.The transitionsKρ=1 andgs=0 divide the phase diagram into four different sectors.[see Fig.1]. Sector(A):Uσ Obviously,the TS correlation dominates over the SS correlation.The ground state is a LL with the TS ordering. Sector(B):U At large distances,due toKρ>1,CS Sdominates overCCDW.The system is a Luther-Emery metal with the SS ordering. Sector(C):U>max{Kρ;Kσ},Kρ<1 and=1.The spin gap is closed.The relations(17)and(18)indicate that the TS and SS correlations are frozen,and that the SDW and CDW correlations exhibit the same decay behavior.To this end,the logarithmic corrections should be taken into account, This hints that the SDW correlation is favored in suppression of the CDW phase.The system is a Mott-insulator with the SDW ordering. Fig 1 The weak-coupling phase diagram of the 1D t-U-V-J model at third filling. Sector(D):Uρ In this paper we have studied the 1D extended Hubbard model of correlated electrons in the case of third-filled band.This model describes a quantum system of itinerant electrons with Coulomb and spin-exchange interactions between electrons at nearest-neighbor sites,in addition to the conventional kinetic hopping and on-site interaction.Moreover,we treatUandVas phenomenological parameters,assuming that they include all the possible contributions and renormalization originating from the electron-phonon coupling.We restrict ourselves to weak interaction regime,where the bosonization approach can be applicative.The low-energy physics is described by the charge and spin fields respectively.With the charge-spin separation hypothesis,the system is decoupled into two independent models.The charge part corresponds to U(1)-symmetric Gaussian model;The spin part corresponds to SU(2)-symmetric sine-Gordon model.With the help of RG analysis,we obtain the spin-gap transition,gs=0,separating the system from a spin-gapped phase forU>Uσto a spin-gapless phase forU2 The weak-coupling phase diagram
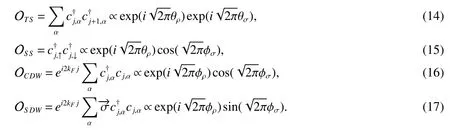





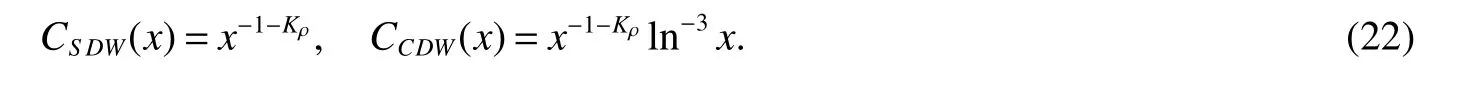

3 Summary
