一类具有状态依赖脉冲控制的SIVS传染病模型的动力学行为研究∗
2016-11-28沈靖云聂麟飞
沈靖云,聂麟飞
(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
0 引言
近年来,传染病动力学行为的研究在预防和控制疾病的传播方面得到了长足地发展,尤其是微分方程形式描述的数学模型吸引了很多学者的关注,研究包括解的非负性、有界性、模型的基本再生数或疾病的灭绝性和持久性的阈值条件等等.文献[1]讨论了一类传染病模型基本再生数R0的计算公式,即R0<1疾病是灭绝的;而当R0>1时,疾病是流行的.Liu等[2]讨论了一类具有年龄结构的SEIR传染病模型,得到解的非负性与有界性,以及疾病的持久性与灭绝性.众所周知,在传染病的预防和控制中,接种疫苗被广泛地视为一种行之有效的控制手段.在传染病的建模过程中,接种疫苗通常有两种方式:连续接种和脉冲接种.对于麻疹、病毒性肝炎、脊髓灰质炎等人类长期面对的传染病,常采用连续接种策略,而对于突发性传染病,如重症急性呼吸综合征(SARS)、人感染高致病性禽流感、流行性感冒等,则通常采用脉冲免疫接种策略.在疾病的预防和控制过程中,具有固定时刻接种疫苗策略不同于连续接种疫苗的策略,事实证明固定时刻接种疫苗策略能更好地帮助疾病的控制.Shulgin等[3]提出了具有固定时刻脉冲接种疫苗策略的SIRS传染病,研究模型疾病消除周期解和地方病周期解的存在性与稳定性,讨论了脉冲免疫控制策略对疾病的消除和持久性的影响.
然而,在很多实际的控制问题中,脉冲控制的发生不依赖于时间,而是依赖于系统所在的状态.例如,对于控制某些特定的疾病(霍乱、艾滋病毒、肝炎等),固定时刻免疫接种并不是一种行之有效地手段.长期来看,我们只可能将这些疾病的染病者数量控制在一个很低的范围,而不可能将其短时间内消除.因此,基于这一想法,文献[4,5]首次提出了具有状态依赖脉冲控制的SIR传染病模型,通过Poincar´e映射、定性分析、拟Poincar´e准则等方法,得到了模型正周期解存在性和稳定性的充分条件,讨论了状态依赖脉冲接种和治疗对疾病的消除和流行的影响.此外,我们也注意到由于状态依赖脉冲控制策略的经济,高效和可操作性而被广泛的应用在种群的收获与控制[6]等众多实际问题中.理论和事实证明,依赖于状态脉冲控制策略比固定时刻控制策略更高效也更合理.
基于上述讨论,本文提出了一类具有状态依赖脉冲控制策略的SIVS传染病动力学模型,研究了状态依赖脉冲控制对疾病消除和控制的影响.
1 预备知识
文献[7]提出了一类具有固定时刻脉冲接种疫苗的自制SIVS传染病模型,该模型将某个地区的人群分为三类:易感者(S),染病者(I)和接种者(V).若基本再生数R0=β/(µ+c)<1,则该模型有一个全局渐近稳定的无病平衡点E0(1,0,0);而当R0>1时,该模型的无病平衡点E0是不稳定的,有唯一的全局渐近稳定的地方病平衡点E∗(S∗,I∗,V∗),其中

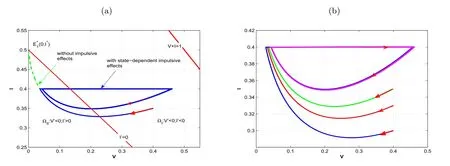
考虑到患病者是传染性疾病传播的根源,因此为了预防和控制某些长期流行的传染性疾病,疾病预防和控制部门需将染病者的数量保持在某个阈值之下,从而控制了疾病的进一步蔓延.基于上述想法,我们将染病的数量作为监测阈值,当染病者的数量高于某个危害阈值时,对易感者进行接种疫苗,减少易感者的数量,进而阻止疾病的蔓延.即,当染病者的数量在时间ti(IH)达到危险阈值IH且接种者的数量较少时,对易感者进行疫苗接种使得易感者的数量变成(1−ω)S((IH)),而接种者数量变成V((IH))+ωS((IH)).这里0 其中VM=(1/(1−σ))(1−IH−(µ+c)/β),本文我们始终假设β>µ+c.即,没有脉冲控制时,模型(2)有唯一的全局渐近稳定的地方病平衡点E∗(S∗,I∗,V∗).根据模型(2)生物背景,我们仅在区域={(x,y,z):x≥0,y≥0,z≥0}上考虑模型(2)的动力学行为.由模型(2)右端函数的性质可知,在上模型(2)的解存在且唯一,更多详细内容见文献[9]. 首先,关于模型(2)解的非负性,下面结论显然成立. 引理1 设(S(t),I(t),V(t))是模型(2)满足初始条件S(t0)≥0,I(t0)≥0,V(t0)≥0的解,则S(t)≥0,I(t)≥0,V(t)≥0,t≥t0. 令R=(−∞,+∞),R+=[0,+∞),:={(V,I):V∈R+,I∈R+}.接下来,我们考虑一般的状态依赖脉冲微分方程 其中f(V,I)和g(V,I)都是定义在R2上连续可微的函数.函数ϕ(V,I)满足ϕ(V,I)=0且充分光滑.为了下文陈述的需要,我们介绍下面两个定义. 设S⊂R2是一个任意的非空集合,P0∈R2是任意一个点.点P0到集合S之间的距离定义为:d(P0,S)=infP∈S|P−P0|.令X(t)=(V(t),I(t))是模型(3)满足初始条件(t0,X0)∈R×R2的解,过点X0=(V0,I0)的正轨线定义为 定义1 (轨道稳定性[9]).模型(3)的解轨线O+(X0,t0)称为轨道稳定的,如果对于任意的ε>0,都存在着一个常数δ=δ(ε)>0,使得对于模型(3)的任何其他的解X∗(t),对于所有的t>t0,当d(X∗(t0),O+(z0,t0))<δ时,均有d(X∗(t),O+(z0,t0))<ε. 定义2 (轨道渐近稳定性[9]).模型(3)的解轨线O+(X0,t0)称为轨道渐近稳定的,如果O+(X0,t0)是轨道稳定的,并且对于模型(3)任何其他的解X∗(t),都存在常数η>0,当d(X∗(t0),O+(X0,t0))<η时,均有limt→∞d(X∗(t),O+(X0,t0))=0. 由于在模型(2)中总人口数保持恒定(不失一般性,假设总人口数为1),因此该控制模型等价于下面的简化模型. 为了讨论模型(4)的动力学行为,我们定义两个截面 对于Σ1∪Σ2上的任意两个点P1(v1,IH)和P2(v2,IH),我们定义P1P2当且仅当v1≤v2;P1≺P2当且仅当v1 显然,水平等倾线dI/dt=0将区域划分成如下两个区域,由模型(4)相空间的几何性质可知,在没有脉冲控制时,模型(4)从ΩI区域出发的任意轨线都将进入到ΩII区域,并且最终趋向平衡点(0,I∗)或者直接趋向平衡点(0,I∗),这正如图1(a)所示.因此,如果IH 首先,当σ∈(0,1−I∗)时,关于模型(4)周期解的存在性和稳定性,我们有下面的定理1. 定理1 如果σ∈(0,1−I∗)且ω(1−IH)>VM成立,则模型(4)存在轨道渐近稳定的正阶-1或阶-2周期解.进一步,模型(4)不存在正阶-k(k≥3)周期解. 证明 由于0<σ≤1−I∗,则水平等倾线dI(t)/dt=0完全位于I+V≤1之内,其中(V,I)∈.即,在第一象限之内,水平等倾线与直线V+I=1没有交点. 任取Σ2上的一点B0(),由模型(4)相空间的几何性质可知,从初始点B0∈ΩI出发的解轨线将进入ΩII区域之内,并且与截面Σ1相交于一点B1(v1,IH).由于受到脉冲的影响,轨线O+(B0,t0)跳跃到截面Σ2,并交截面Σ2于点().因为ω(1−IH)>VM,所以B1.重复上述过程,我们可以得到两个点列{Bn(vn,IH)}和()},n=0,1,2,···.关于点B0和点的位置关系,我们有下面三种情况: 情况1:B0=B1.模型(4)存在着一个正阶-1周期解. 情况2:0.如果0,那么.进一步,B1≺B2,即v1 (i)=B0.我们有=,则模型(4)存在一个正阶-2周期解. (ii)0.如果0,那么.因此,,和的位置关系为0.由模型(4)解的唯一性有B1≺B3≺B2.进一步,由模型(4)的第三个方程和v1 即 因此,由单调有界数列必有极限可知.模型(4)存在一个轨道渐近稳定的正阶-1周期解. (iii).B0.如果B0,则有B3≺B1.进一步,我们有和B2≺B4.重复上述过程,我们可以得到 即 从上述讨论可知,模型(4)存在轨道渐近稳定的正阶-2周期解. 情况3:B0.类似于情况2的讨论,模型(4)存在轨道渐近稳定的正阶-1或阶-2周期解. 综上所述,当σ∈(0,1−I∗)且ω(1−IH)>VM成立时,模型(4)存在轨道渐近稳定的正阶-1或阶-2周期解,且模型(4)不存在正阶-k(k≥3)周期解. 下面,我们讨论σ∈(1−I∗,1]时的情形.在这种情形下,水平等倾线I(t)=0和直线V+I=1相交于第一象限内的某一点,则该交点的纵坐标为Ih=1−(µ+c)/σβ.关于模型(4)正周期解的存在性与稳定性,我们有下面的结论. 定理2 对于任意的σ∈(1−I∗,1],如果ω(1−IH)>VM且Ih 由于定理2的证明与定理1类似,故这里省略. 本文我们提出了一类具有状态依赖脉冲免疫控制策略的SIVS传染病动力学模型.通过运用常微分方程定性理论、Poincar´e映射、微分不等式等方法,建立了模型(4)正阶-1或阶-2周期解存在性和轨道渐近稳定性的判别准则.下面我们将通过数值模拟来验证理论结果的正确性和状态依赖脉冲控制策略的可行性.在模型(4)中,固定参数σ=0.25,β=0.6,µ=0.1,c=0.2,ω=0.75,θ=0.2和IH=0.4.容易计算R0=β/(µ+c)>1,ω(1−IH)>VM和σ∈(0,1−I∗].因此,在没有脉冲作用时,模型(4)存在唯一的地方病平衡点(0,I∗)=(0,0.5),且是全局渐近稳定的,这正如图1(a)中绿线所示.由于脉冲控制的影响,模型(4)存在一个从(V(0),I(0))=(0.4,0.35)出发的正阶-1周期解(V∗(t),I∗(t)),正如图1(a)中蓝线所示.进一步,图1(b)表明该周期解是轨道渐近稳定的.这表明数值模拟的结果和定理1的理论结果完全一致. 在没有脉冲控制时,模型(4)中免疫接种者的数量呈指数形式减少,进一步,正如图2(a)中红色线所示.由于脉冲控制策略影响,模型(4)中免疫接种者的数量会呈现周期性的变化,正如图2(a)中蓝色线所示.此外,图2(b)中红色线所示在没有脉冲控制作用时,模型(4)中染病者的数量在一定的时间内会趋向平衡状态0.5处.但是,在脉冲控制下,模型(4)中染病者的数量会呈现周期变化的趋势,并保持在一个较低的范围之内,正如图2(a)中蓝色线所示.理论结果和数值模拟显示,在状态脉冲控制策略下,我们可以将染病者的数量作为监测阈值,通过对易感者进行免疫接种,就可将染病者的数量保持在一个较低的水平,从而控制了疾病的蔓延. 图1 模型(4)正阶-1周期解的存在性与轨道渐近稳定性,控制参数σ=0.25,β=0.6,µ=0.1,c=0.2,ω=0.75,θ=0.2和IH=0.4<0.5 图2 模型(4)的时间序列图,控制参数σ=0.25,β=0.6,µ=0.1,c=0.2,ω=0.75,θ=0.2,IH=0.4<0.5和V0=0.4,I0=0.32


2 主要结论






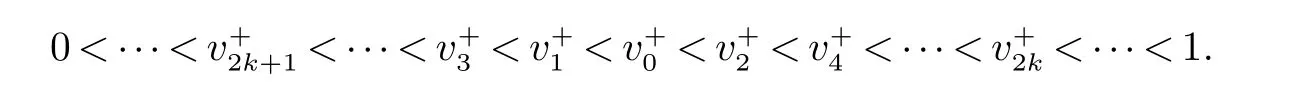
3 数值模拟和讨论