多边信息不对称下拥有竞争制造商的供应链决策

2016-11-28计国君王东

统计与决策 2016年20期

关键词：谎报零售商制造商

计国君,王东

(1.两岸关系和平发展协同创新中心;2.厦门大学管理学院,福建厦门361005)

多边信息不对称下拥有竞争制造商的供应链决策

计国君1,2,王东2

(1.两岸关系和平发展协同创新中心;2.厦门大学管理学院,福建厦门361005)

文章研究两个竞争制造商和一个零售商共同面临成本信息不对称风险时的供应链决策问题。运用Stacke lb erg博弈理论,在制造商和零售商分别拥有私人成本信息时,探讨供应链成员的三方博弈机制以及博弈结果对供应链系统绩效的影响。研究结果表明,相比不谎报行为,无论是制造商还是零售商都会通过谎报策略获取更多利润,最终会实现三方都采取谎报行为的Nash均衡,但整个系统效率降低,而且当制造商竞争达到一定程度时,供应链成员会陷入囚徒困境。

多边信息不对称;竞争型制造商;谎报信息;囚徒困境

0 引言

供应链协调运作的关键在于供应链中的节点企业实现信息传递和共享[1]。随着经济一体化以及信息技术的快速发展,谋求合作和信息共享已经成为企业间的共识。但是由于供应链的成员均是独立的经济个体,为了自身的利益以及能够在市场竞争中处于优势,通常会对链中其他成员隐瞒一些重要的信息,如成本信息、需求信息等,导致在供应链管理中普遍存在信息不对称的情况。这种情况由于竞争关系存在体现得尤为明显,企业会极力隐瞒私人信息防止泄露,这使得供应链节点企业之间的信息愈发不透明。链中成员会更少的将信息透露给竞争对手,从而利用占有信息优势以增加议价能力,与此同时花费更多的时间和成本去识别市场信息的真实性,导致整个供应链的效率下降。因此,对存在多边信息不对称下竞争型企业的决策机制进行研究具有重要的现实意义。

本文考虑由两个竞争型制造商和一个共同零售商组成的供应链系统,研究当供应链成员均存在私人成本信息的情况下的三方博弈问题,分析谎报行为如何影响链中成员和整个系统利润,并讨论制造商竞争强度对决策结果以及系统绩效的影响。

1 模型建立与求解

1.1 问题描述与符号说明

考虑由两个竞争型制造商和一个共同零售商组成的二级供应链,制造商和零售商分别拥有私人生产成本信息和销售成本信息情形的谎报策略。假设制造商为市场的Stacke lb erg领导者,且制造商之间存在Ber tr and竞争。令Si为供应链成员i(i=m，n，r)的决策,Si∈{y，N},其中Y=谎报,N=不谎报,则系统策略集为S={(Sm，Sn，Sr)|Si= y orN}。目的探讨不同策略组合供应链成员的收益值,寻求三方博弈下的Nash均衡策略并探讨制造商竞争强度对链中成员以及系统均衡解的影响。

符号说明:

c为该类产品的真实生产成本;

Cr为该类产品的真实销售成本;

θi为供应链成员i的谎报因子(i=m，n，r);

wj、pj分别为产品j的批发价和零售价(j=1，2)。

根据颜荣芳(2013)和张克勇(2008)的研究结果,假设产品的市场需求只与该产品以及竞争产品的零售价有关,令a为该类产品的市场基本需求,β为制造商竞争系数(0＜β＜1),则产品j的市场需求Dj=a-pj+βp3-j, (j=1，2),制造商m公开的市场利润为:

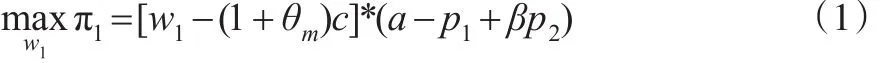
制造商n公开的市场利润为:

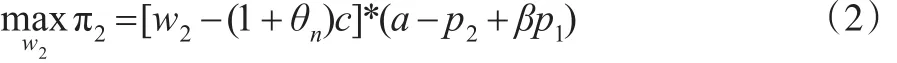
零售商r公开的市场利润满足:

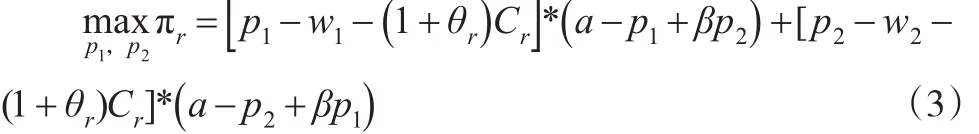
制造商m真实的市场利润为:

制造商n真实的市场利润为:

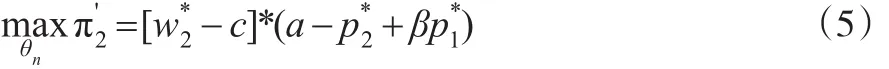
零售商r真实的市场利润为:

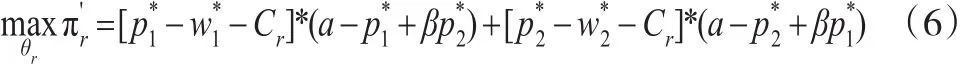
这样,整个供应链系统总利润满足:

1.2 模型建立与分析

首先考察(谎报,谎报,谎报)模型。在该模型中,两个竞争制造商和零售商均采取谎报的策略,分别考虑制造商和零售商之间的Stacke lb erg模型以及制造商之间的Ber tr and模型,博弈过程如下:零售商r和制造商m、n确定最优谎报值;制造商m和制造商n分别确定产品1和产品2的批发价;零售商r确定产品1和产品2的零售价。采用逆序算法求解,先考虑零售商r的定价决策。

讨论πr关于零售价的凹凸性,此时关于πr的二阶海赛矩阵H(πr)满足海赛矩阵一阶顺序主子式||-2=-2＜0,二阶顺序主子式海赛矩阵为负定,即πr关于零售价p1，p2是联合凹的。则存在唯一最优解组合在该临界点处取得局部最大值,即全局最大值。

对πr关于p1，p2求偏导,并令一阶偏导数为零,有:

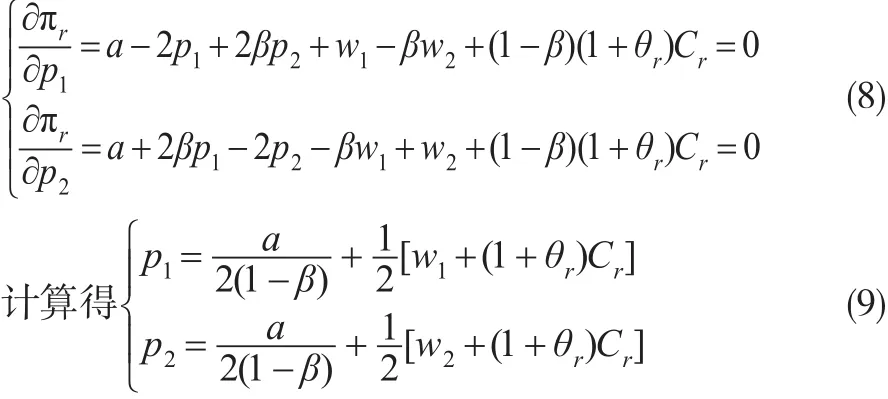
分别代入到式(1)和式(2)中,有:

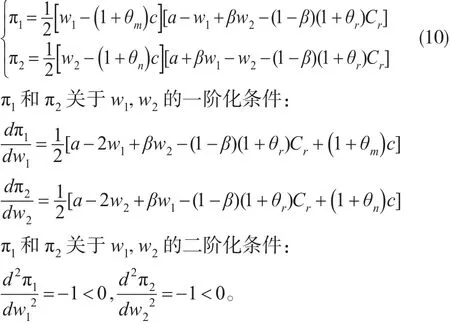
将式(11)和式(12)式代入到式(4)、式(5)以及式(6)中,得到链中成员的真实利润函数满足:

则供应链成员最大利润值分别为:

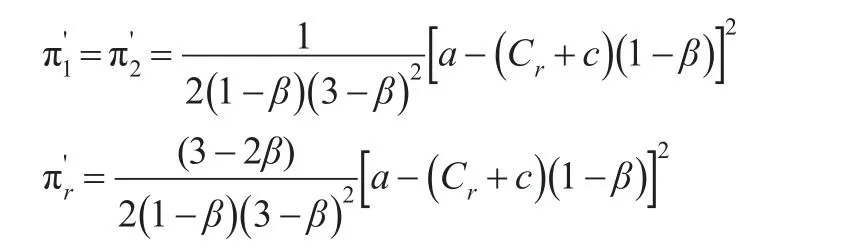
类似(谎报,谎报,谎报)模型的计算过程,根据其他七种模型中不同成员的谎报因子是否为零分别代入式(13)、式(14)以及式(15)中,得到链中成员谎报因子最优值以及利润值。结果如表1和表2所示。

表1 八种谎报策略下制造商和零售商的谎报因子最优值

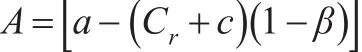
表2 八种谎报策略下制造商和零售商的利润函数最优值

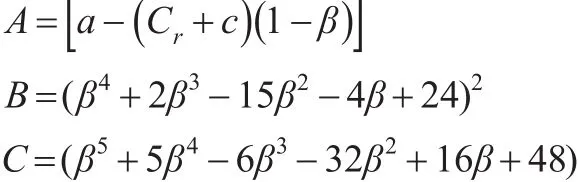
2 理论结论

对表1和表2中的成员利润和谎报因子数值进行分析和比较,可以得出如下结论:

即无论链中其他成员的策略如何,对成员i总有谎报收益值大于不谎报收益值,也就是说谎报总是有利可图。

以制造商m为例,在链中其他成员策略不变的情况下,当制造商m采取不谎报策略时,零售商谎报额度增大,制造商n谎报额度减少,导致制造商m的批发价w1减小,市场份额增加,但利润是减少的。制造商m的部分利润被零售商r和制造商n共同侵占,即零售商r和制造商n获得了更多的收益。

结论2:供应链成员最终决策策略组合为(Y,Y,Y)。

考虑制造商m和制造商n以及零售商r的三方博弈矩阵,如表3所示。

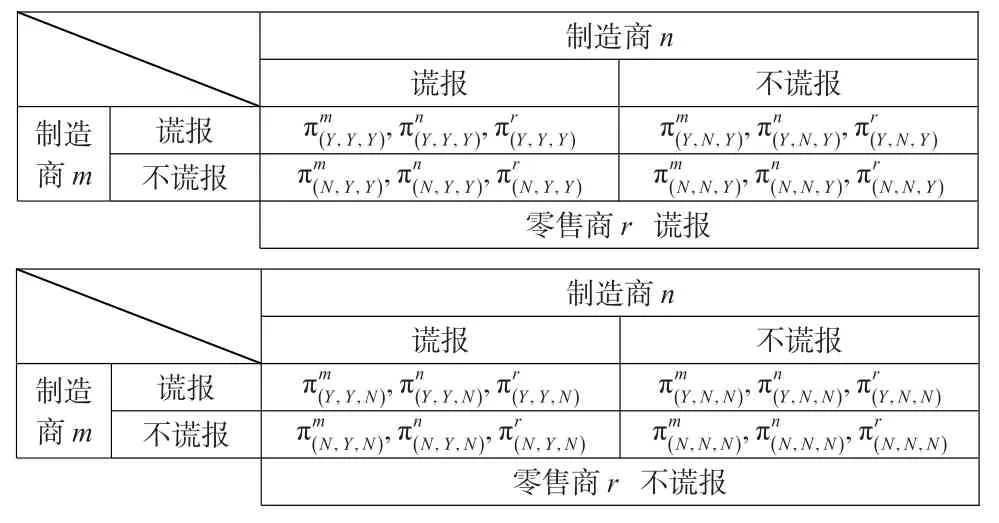
表3 三方博弈矩阵

结论3:系统最优决策=(N,N,N)。

结论4:当竞争系数β满足条件β1＜β＜β2时,供应链成员陷入囚徒困境时

由于在(Y,Y,Y)和(N,N,N)策略下,制造商m和制造商n的利润相同,因此只考虑制造商m的情形。计算可知当0＜β＜β时,πr＞πr,πm＜πm;β＜

1(y，y，y)(N，N，N)(y，y，y)(N，N，N)1时,(N,N,N)策略为Pareto最优,但是此时个体策略为(Y,Y, Y),链中成员陷入囚徒困境。这是由于不同谎报策略下制造商和零售商收益增长的不一致引起。当竞争强度较小时,制造商倾向于采取不谎报策略,零售商倾向于采取谎报策略;而当竞争强度较大时,结论正相反。事实上由于本文理性人的假设,链中节点成员的决策出发点是基于个人利益最大化,使得个体策略与群体策略相矛盾。该结论也佐证了在非零和博弈中Nash均衡与Pareto最优相冲突的结论。

该结论表明产品替代系数越大,成员利润和系统总利润越多,即供应链的利润将随着产品可替代系数即竞争强度的增加而增加。这是因为制造商之间的竞争会提高产品需求,促进市场购买力导致供应链成员利润的提高,同时系统总利润也增加,鉴于此选择竞争无论对链中成员还是整个供应链系统都是有益的。

3 数值分析

下面利用数值案例来进一步验证上述结论。设a=50，Cr=3，c=2，β=0.8。计算链中各成员在不同策略下的利润值,结果如表4所示:

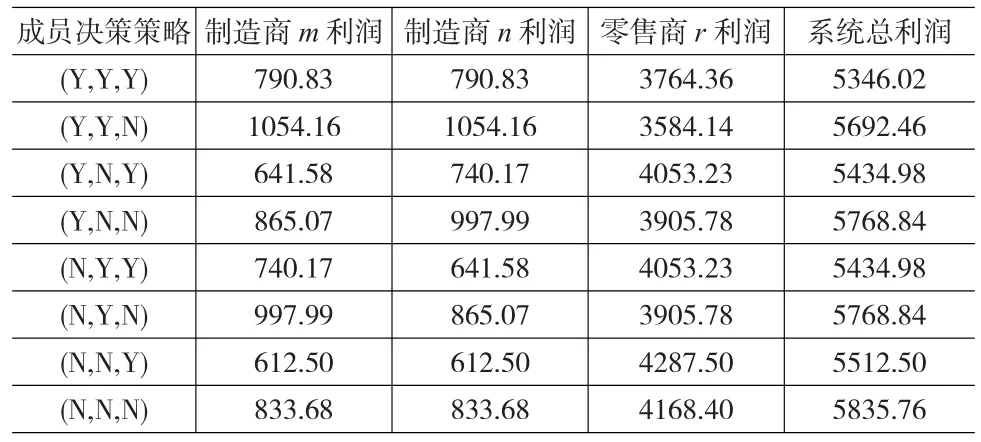
表4 八种策略下成员和系统利润值

从表4可知,对成员i而言谎报信息的收益值恒大于不谎报信息的收益值,谎报信息得到的额外收益来源其他两个成员的收益,造成其他两个成员收益值减少,系统的总利润也减少。

下面考虑制造商的竞争强度β对链中成员和系统总绩效的影响。设a=7，Cr=2，c=1,利用MATLAB软件分析结果如图1和图2所示(由于制造商m与制造商n的收益呈对称关系,因此只考虑制造商m的收益情况)。

从图1和图2可知,竞争强度β与制造商和零售商的收益呈正相关关系,即竞争强度越大,链中成员的收益越大。当强度系数β超过0.7时,制造商和零售商的收益急剧增长。

考虑竞争系数β对(Y,Y,Y)和(N,N,N)两种策略组合下的链中成员收益的变化,结果如图3所示:

通过计算可以得知β1=0.5823,β2=0.82115,因此当β∈(0.5823，0.8215)时,链中成员的个人决策为(Y,Y,Y),系统Pareto最优决策为(N,N,N),供应链成员陷入囚徒困境。考虑横坐标轴为竞争系数,纵坐标轴为(Y,Y,Y)策略下成员收益值与(N,N,N)策略下成员收益值的差值,则得到制造商的差值与零售商差值共同为负所围成的区域即为囚徒困境区域,如图4黑色阴影部分所示:

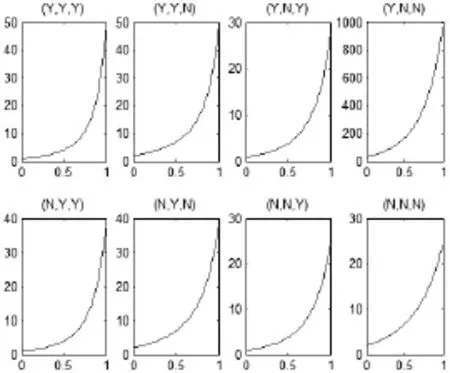
图1 竞争系数β与制造商m收益的关系

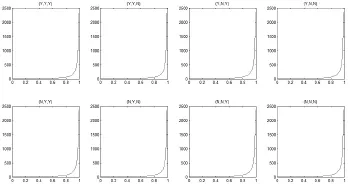
图2 竞争系数β与零售商r收益的关系

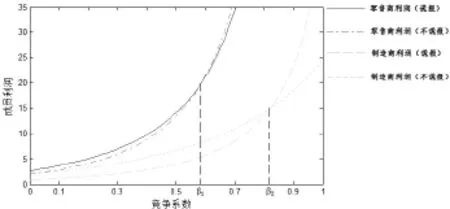
图3 竞争系数β与成员利润差额

图4 竞争系数β与囚徒困境区域

通过表4和图1至图4中的数据,可知:(1)三方博弈下的(谎报,谎报,谎报)策略是唯一Nash均衡策略,但并不是最优策略。虽然链中各成员都可以通过谎报信息来获取超额利润,却是建立在其他成员的利润减少的基础之上,并且减少的利润大于增加的利润,市场的利润呈现负增长。虽然短期内可以利用信息上的不对称获取利润,但是系统却难以长期稳定发展。只有通过成员间的信息沟通和共享,协调各方利益,方能实现系统的良性发展。(2)竞争对供应链的所有成员是有益的。对制造商来说,竞争可以增加市场需求,促进消费者购买力;对零售商来说,由于制造商之间的竞争一方面扩大市场需求,另一方面制造商为了争夺市场,使得零售商有了更大的议价能力,市场利润也会急剧增长。(3)针对不同的竞争强度供应链成员应该采取不同策略。当竞争强度β≤β1时,零售商更倾向于谎报信息;β≥β2时,制造商更倾向于谎报信息。在这两种情况下,难以实现各链中成员之间的策略协调,成员只有共同采取谎报信息的唯一策略。而当β1＜β＜β2时,不谎报策略才是所有成员的严格优势解,但是由于链中成员难以信息共享,使得任何一方都不愿意放弃谎报策略从而面对利润下降的风险,最终导致利润的减少和系统效率的下降。

4 结论

本文从多边成本信息不对称角度出发,研究由两个竞争型制造商和一个共同零售商构成的二级供应链中,当存在信息谎报时供应链成员的决策机制。对比分析八种策略组合下各成员和系统收益值发现:无论其他成员是否谎报信息,对于决策者来说总会采取谎报策略,三方博弈最终会实现(谎报,谎报,谎报)的唯一Nash均衡。虽然采取谎报行为会提高决策者的利润,但是却损害其他成员的利益,导致整个供应链效率降低,收益减少,不利于系统的稳定和发展。另外制造商之间的竞争会提高产品需求,促进市场购买力,竞争强度越大,成员和系统收益越大。但是当竞争系数大于0.5823且小于0.8215时,此时的三方博弈模型存在Pareto最优解(不谎报,不谎报,不谎报),这与Nash均衡相矛盾,产生囚徒困境。

本文基于供应链成员的三方博弈模型得到各成员均谎报策略的Nash均衡,考察的是单周期的成员策略,因此该策略只是短期内的可行解,并不是系统最优解,从长远来看谎报行为会损害制造商、零售商和消费者的利益。制造商基于信息不对称的恶性竞争虽然短期内可以占有市场,但是通过谎报信息的竞价策略难以持续,对应的零售商边际收益也会减少。而信息不对称将会导致消费者搜寻成本增加,产品效用减少,购买力下降,这对市场是不利的。因此,只有实现信息沟通和共享,协调各方利益,才能实现市场的良性竞争。具体可通过以下几种措施:(1)企业应从长远出发,意识到短期内的投机行为的坏处,加强企业之间合作,建立健全信息共享机制,实现供应链上下游的信息沟通,杜绝谎报瞒报行为的存在;(2)鼓励消费者行使监督市场权利,如消费者揭发激励机制,及时监督企业行为,发现企业存在不良行为及时举报;(3)政府完善法律法规,规范市场运营,通过搭建信息平台构建信息共享环境,提高信息的准确性与及时性,引导企业的社会责任意识。即通过企业自律、顾客监督、政府三位一体的信息对称机制来维护市场的长期稳定。

本文对于制造商之间竞争的假设是Ber tr and竞争,事实上由于市场上成员力量的不同,制造商之间的竞争模式也不尽相同。因此,考虑不同的竞争模式对成员策略的影响是值得进一步研究的问题。此外本文模型还可以扩展为由竞争型制造商和竞争型零售商构成的双链混合竞争模型。

[1]BarrattM.Understanding the Meaning Of Collaboration in the Supply Chain[J].Supply Chain Management,2004,9(1).

[2]w ei J,Govindan K,Li y,etal.Pricing and Collecting Decisions in A Closed一loop Supply Chain w ith Symmetric and Asymmetric Information[J].Computersand OperationsResearch,2015,54.

[3]Liy,Xu X,Zhao X,etal.Supply Chain Coordinationw ith Controllable Lead Time and Asymmetric Information[J].European Journal of OperationalResearch,2012,217(1).

[4]徐鸿雁,陈剑.不对称信息下对异质销售商激励及产品定价[J].系统工程学报,2011,26(2).

[5]王刊良,王嵩.非对称信息下讨价还价的动态博弈:以三阶段讨价还价为例[J].系统工程理论与实践,2010,30(9).

[6]徐晓燕,吴三平.生产成本信息不对称的两级供应链协调研究[J].系统工程学报,2009,24(1).

[7]李永超,曹二保.不对称信息下需求扰动是的供应链决策模型[J].统计与决策,2011,(4).

[8]李怡娜,徐学军.信息不对称条件下可控提前期供应链协调机制研究[J].管理工程学报,2011,25(3).

[9]王新辉,汪贤裕,苏应生.双边成本信息不对称的供应链协调机制[J].管理工程学报,2013,27(4).

[10]黄永,孙浩,达庆利.制造商竞争环境下基于产品生命周期的闭环供应链的定价和生产策略研究[J].中国管理科学,2013,21(3).

[11]王莺,李军.竞争制造商供应链合作收益分配研究[J].统计与决策,2010,(18).

[12]颜荣芳,程永宏,王彩霞.再制造闭环供应链最优差别定价模型[J].中国管理科学,2013,21(1).

[13]张克勇,周国华.基于博弈论的闭环供应链差别定价协调问题[J].经济问题,2008,(9).

(责任编辑/易永生)

F252