增量投入产出表的编制方法研究

2016-11-28李国璋陈南旭

统计与决策 2016年20期

关键词：行列调价纯收入

李国璋,陈南旭

(兰州大学经济学院,兰州730000)

增量投入产出表的编制方法研究

李国璋,陈南旭

(兰州大学经济学院,兰州730000)

文章修正完善了增量投入产出表表式,包括一般表式和反映软投入贡献的表式两种;重点研究了增量投入产出表的一般编制方法:基础投入产出表的选取和部门(栏目)合并、可比价变换与两年度投入产出表相减是增量投入产出表的一般编制步骤;对调价系数确定和选取的两种可能途径做了实证比较,认为逐项确定更加符合实际应用。对于行列平衡调整,认为应以“总产出”为准,用减法得到初始投入,并采用动态分摊法处理偏差。

增量投入产出表;调价系数;行列平衡

0 引言

增量投入产出表是一份由基期和目标期两份投入产出表(已换算成可比价)相减得到的跨期投入产出表。与静态、连续型动态、离散型动态投入产出表相比,增量投入产出表的编制可能性更大,在经济增长因素分析和经济结构分析与预测等方面的解释力更强。

静态投入产出表反映单一时点上的各类产品投入与产出间的内在联系,无法给出一个连续的动态描述。连续型动态投入产出表把生产增长看作是一个瞬时的连续过程,不具有现实经济意义和操作可能性。离散型动态投入产出表可以计算出投资系数矩阵,虽然能够在一定程度上反映社会生产中的变化与发展,但受限于其编制假设(各部门新增生产能力都能得到充分利用、各期直接消耗系数矩阵与投资系数矩阵不变),只能反映技术、政策不变情况下的跨期社会生产状况。增量投入产出表描述的是一个经济系统在特定时间区间内各部门产出增量与投入增量的关系,它可以回答j(j=1，2，…，n)部门增加单位数量产品需要n个部门增加的中间投入数量问题,还可以由j(j=1，2，…，n)部门初始投入中的纯收入增量分解出软投入对该部门产出增长的贡献水平,这些是静态投入产出表和连续型、离散型动态投入产出表在应用过程中所无法做到的。

李国璋(1995)首次提出增量投入产出表概念并编制了中国1987—1990年和甘肃省1987—1990年增量投入产出表[1]。在此基础上,武玉洁(2008)编制了中国1997—2002年16部门增量投入产出表[2],闫来旗(2011)分别编制了中国1997—2002年、2002—2007年13部门增量投入产出表[3],陈南旭(2012)编制了甘肃省2002—2007年16部门增量投入产出表[4]。此外,陈宏伟(2010)[5]、张唯实(2012)[6]戚磊(2012)[7]等在测算软投入贡献率时均对编制增量投入产出表做了有益尝试。

增量投入产出表具有重要的应用价值,因此有必要探讨编制增量投入产出表的方法,对增量投入产出表及其上述编制实践做出归纳和修正,以便编制出精确度较高的增量投入产出表应用于实际。

1 增量投入产出表的编制方法

1.1 表式

增量投入产出表的表式主要考虑两种形式:一种是一般表式,整体设计参照静态价值形态投入产出表(三象限表式),第I象限是中间投入(中间产品)增量,第II象限是最终产品增量,第III象限是初始投入(增加值)增量;另一种是对一般表式中“纯收入增量”的分解——反映软投入贡献的表式,与表1不同的是,表2将“纯收入增量”进一步区分为软投入贡献和硬投入贡献。

表1 增量投入产出表的一般表式

对于反映软投入贡献的表式,由上述一般表式各列分解出软投入贡献而得到,即表2。

表2 反映软投入贡献的增量投入产出表表式

在对一般表式的第j列进行分解时,上标(H)表示来自硬投入增量的贡献,上标(S)则表示来自软投入质量变化的贡献。软投入贡献可以带来成本的减少,其减少量在理论上全部转化为纯收入。在这个意义上,认为软投入组合对经济增长的贡献属于纯收入增量的一部分是合理的。

因此,j部门的软投入组合贡献可以表示为:

软投入组合对经济增长的贡献率可以表示为:

1.2 编制方法

编制增量投入产出表,关键一步是编制调价后的投入产出表。因此,本文以下内容主要围绕如何编制调价后的增量投入产出表展开。

1.2.1 调价系数的确定和选取

编制增量投入产出表需在基期当年价格的基础上根据目标期当年价格确定一组调价系数。这里,涉及两种可能途径:一种是模型估算,一种是逐项确定。

(1)模型估算

主要通过可比价投入产出表价格系数理论计算模型(下文简称计算模型或调价系数计算模型)[8]解出编制增量投入产出表所需调价系数。

设目标期关于基期的各部门调价系数为pi(i=1,2,…, n),固定资产折旧调价系数为pD,劳动报酬调价系数为pV,纯收入调价系数为pM。则对于合并部门后的目标期投入产出表,从行向看有:

从列向看有:

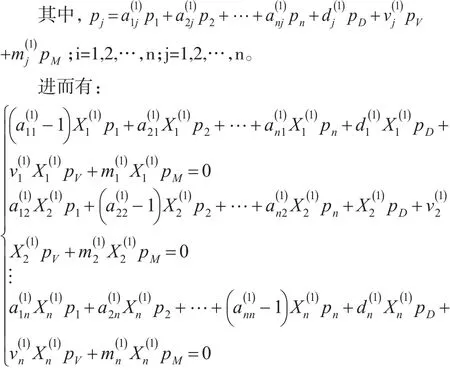
该方程组可求出n+3个调价系数(p1,p2,…pn, pD,pV,pM):在无任何限制条件下该方程组有无穷多解;但若给出n+3个调价系数中任意3个的值,方程组变为系数行列式不为零的含有n个方程的n元线性方程组,则由克莱默法知其有唯一解。若p1,p2,p3为已知数值,通过“Chasys Math”或Matlab可解出其余n个调价系数的值。

单从公式推导上看,通过模型估算调价系数是可行的,若能得到目标期关于基期的各部门调价系数、固定资产折旧调价系数、劳动报酬调价系数以及纯收入调价系数中的任意3个,其余n个调价系数即可求得。

但在实际操作过程中,利用上述线性方程组得到的解,不可能是n个部门的调价系数。这是因为当n个生产部门的价格变化后,为了适应这一变化,n个生产部门的中间投入结构必然发生变化。这样,n个生产部门进行调价,对应直接消耗系数矩阵必然发生变化。调价系数对应的不应该是调价前的直接消耗系数矩阵,而是变化了的直接消耗系数矩阵。利用调价前的直接消耗系数矩阵显然无法解出实际的调价系数。因此,本文提出另一种途径,逐项确定n个生产部门和初始投入共n+3个调价系数(包括各部门调价系数、固定资产折旧调价系数、劳动报酬调价系数以及纯收入调价系数)。

(2)逐项确定

理论上,准确的调价系数源于各部门的实际价格指数,可据此逐个确定目标期投入产出表中各行项的调价系数,分5类讨论如下:

①工业各部门调价系数,以工业生产者出厂价格分类指数为基础来确定。工业生产者出厂价格分类指数可以从国家统计局网站或各省统计局获取。部门合并后,为保证口径一致,新部门的工业生产者出厂价格指数由合并前的各部门工业生产者出厂价格分类指数的加权平均构成,权数为各部门产值占其新部门总产值的比重。工业各部门调价系数为部门合并后新部门基期和目标期间工业生产者出厂价格指数的连乘积。

②农林牧渔业、建筑业、第三产业调价系数,以指数替代法确定。农林牧渔业调价系数以基期与目标期间农产品生产价格指数的连乘积来替代确定。建筑业调价系数以基期和目标期间建筑安装工程固定资产投资价格指数的连乘积替代确定,方法同农林牧渔业调价系数。第三产业调价系数以其基期与目标期间各产业价格指数或选取的相应替代指数加权平均确定。

③固定资产折旧调价系数,以指数替代法确定。固定资产调价系数以基期和目标期间固定资产投资价格指数的连乘积替代确定。

④劳动报酬调价系数,以物价指数替代得出。劳动报酬是居民收入的主要来源,主要用于消费、储蓄和投资。考虑其用途和实际购买力等因素,可直接采用基期和目标期间居民消费价格指数(CPI)的连乘积近似替代劳动报酬调价系数。

⑤纯收入调价系数,以加权平均法计算得出。纯收入由生产税净额和营业盈余两部分组成。若要得到纯收入调价系数,应先计算出生产税净额调价系数和营业盈余调价系数,然后采用加权平均法求出纯收入调价系数。

(3)实证比较

为说明模型估算与逐项确定的差异,本文以编制1987—1992年、1992—1997年、1997—2002年、2002—2007年增量投入产出表所需调价系数为例,比较两种途径的测算结果,给出模型估算的平均测算误差,验证上文所述“由方程组解出的值并不是实际的调价系数”。

将各时期(1987、1992、1997、2002、2007年)全国投入产出表均合并为4部门(农林牧渔业、工业、建筑业、第三产业)投入产出表,分别根据途径1(模型估算)和途径2 (逐项确定)计算各时期调价系数,见表3。

表3 各时期增量投入产出表调价系数测算结果

不难发现,途径1与途径2在估算结果上差异较大。从效果上看,途径1在实际操作中准确性却较低,估算结果中负值的出现更印证其不是实际的调价系数。

表4 途径1分时期的测算误差(以途径2确定的调价系数为标准)(单位:%)

根据表4,途径1在测算各部门调价系数时,平均测算误差显著,1987—1992年间为560.27%,1992—1997年间为-222.48%,1997—2002年间为-1382.14%,2002—2007年间为-1109.75%。显著的误差使途径1在实际应用中失去了意义,但这并不意味着途径1全无可取之处,其测算的各部门调价系数误差之比完全可作为代入调价系数后平衡行列时的一个依据。

逐项确定的调价系数与价格指数一一对应,较之模型估算的解更加符合应用实际。采用途径2(逐项确定)作为调价系数确定和选取的方法凸显了可比价变换的意义。

调价系数的代入常常并不会使目标期投入产出表直接满足行列平衡关系,行和列间存在偏差,因此在得到编表所需的各项调价系数后,对目标期投入产出表进行可比价变换,面临的问题是代入调价系数后如何调整行列,使其平衡。这里,涉及初始投入的调整和行列偏差的分摊。

1.2.2 行列平衡——用减法得到初始投入

行列平衡就参照标准而言,可选指标有两个:“总产出”和“总投入”。“总产出”代表行向关系,“总投入”代表列向关系。选择以“总产出”为准,调整初始投入;选择以“总投入”为准,则调整最终产品。投入产出表进行可比价变换时,行向关系中,pi为单个部门对应的调价系数;列向关系中,pM,为各部门、固定资产折旧、劳动报酬与纯收入调价系数的加权平均。由可比价变换前对应行列知,“总投入与“总产出不相等的原因是pj与pi不相等。比较二者,pi比pj更具合理性,单个部门调价系数测算出现误差时,受到的影响要小于所受的影响。

由此,本文在平衡行列时,选择以“总产出”为准,调整初始投入。其要点是:把n个部门的调价系数沿着行向乘进去,然后运用调价后n个部门总产出等于调价后n个部门总投入的基本条件,用各部门的总产出减去该部门的中间投入合计,得到该部门的初始投入合计。由李强(1998)主持,国家统计局与香港中文大学合作编制的《可比价投入产出序列表》,包括1981年、1983年、1987年、1990年、1992年和1995年六个年份的投入产出表采用了类似处理[9];刘起运、彭志龙(2010)编制的中国1992—2005年可比价投入产出表也沿用了这一做法[10]。需要说明的是,这种方法简便易行,只是得到的初始投入精确度难以把握,可能会给运用初始投入分析软投入贡献造成困难。

1.2.3 行列平衡——按权重动态分摊行列偏差

行列平衡就偏差处理而言,可选方法有两种:一是动态分摊法,二是初始投入修正法。动态分摊法以“总产出”为准,将调价后对应各行列“总产出”与“总投入”的实际偏差按照一定权重(如方法1确定的n+3个调价系数测算误差权重)分摊到各列相应项。动态分摊法是一个多次分摊的模拟过程,每次分摊都会引起总产出的变化,直至行列平衡。随着分摊的进行,“总产出”会与其对应列的各项之和(每次分摊后的总投入)不断接近,反复求极限后,“总投入”将与“总产出”相等。动态分摊法的每次分摊公式为:各列相应项分摊后数值=各列相应项分摊前数值+(各列相应项对应调价系数按方法1测算的误差/各列相应项对应调价系数按方法1测算的误差之和)×(总产出-各列分摊前总投入)。

初始投入修正法是以“总产出”为准,将调价后对应各行列“总产出”与“总投入”的实际偏差按照一定权重(如方法1确定的固定资产折旧、劳动报酬与纯收入调价系数测算误差权重)全部分摊到各列的“初始投入”。初始投入修正法只需进行一次分摊即可完成,其分摊公式为:各列初始投入中相应项分摊后数值=各列初始投入中相应项分摊前数值+(各列初始投入中相应项对应调价系数按方法1测算的误差/各列初始投入中各对应调价系数按方法1测算的误差之和)×(总产出-各列分摊前总投入)。

比较两种方法,动态分摊法覆盖第Ⅰ、Ⅲ象限的各项数据;初始投入修正法只涉及第Ⅲ象限;在偏差分摊的精确度上,动态分摊法要高于初始投入修正法。因此,本文选择动态分摊法平衡行列。

目标期投入产出表可比价变换后,根据增量投入产出表的定义及基期、目标期的时间先后顺序,将两年度投入产出表相减即完成增量投入产出表的编制。

2 编制实例与应用

2.1 编制实例

增量投入产出表的编制以两年度投入产出表为基础。这里,以编制中国2005—2010年增量投入产出表为例,具体说明。

首先,选择中国2005年42部门投入产出延长表和2010年41部门投入产出延长表为基础数据,确定2010年为基期,2005年为目标期。

其次,根据使用需要,对两年度投入产出表进行部门(栏目)合并。如关注2005—2010年间全国产业结构变化状况,可先将2005年投入产出表中的“工艺品及其他制造业”和“废品废料”合二为一,将“生产税净额”与“营业盈余”合并为“纯收入”,将“最终使用”与“进口”、“其他”合并为最终产品,使其与2010年投入产出延长表具有相同的部门、栏目分类和个数(41部门);而后将两年度投入产出表均合并为4部门(农林牧渔业、工业、建筑业、第三产业)。

第三,根据部门及栏目合并情况,计算2005年可比价投入产出表换算所需的各部门、各栏目调价系数(按2010年当年价格)。表5列出了途径1和途径2的测算结果。

表5 2005一2010年增量投入产出表调价系数测算结果

根据途径2得到各调价系数,并将途径1测算的各部门调价系数误差之比作为接下来行列平衡的一个标准。由表6,途径1各部门、栏目的测算误差之比为:-1:1.04: 39.30:-12.39。

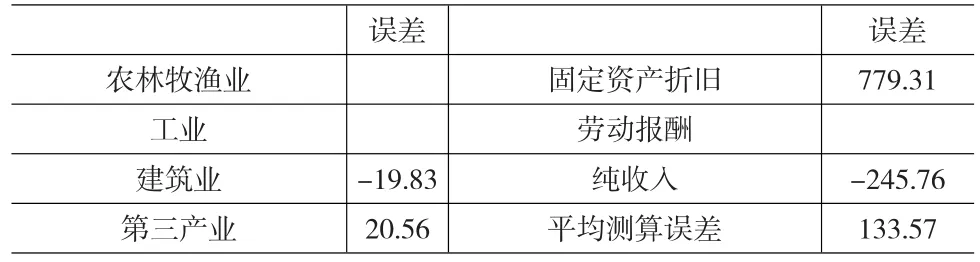
表6 途径1的测算误差(以途径2确定的调价系数为标准,时间段为2005一2010年)(单位:%)

第四,根据各调价系数对2005年投入产出延长表做可比价变换:将除“中间投入小计”、“增加值合计”、“总投入”外的各行乘以对应调价系数,同时得出“中间投入小计”、“增加值合计”、“总投入”;比较“总产出”与“总投入”:若相等,则可比价变换完成,若不相等,则以“总产出”为准,用减法得到初始投入,使用动态分摊法平衡行列。这样,得到的新的投入产出表即为按2010年当年价格计算的2005年4部门可比价投入产出表。

第五,用部门合并后的2010年4部门投入产出表各项减去2005年4部门可比价投入产出表对应各项,得到的新表即为中国2005—2010年增量投入产出表。

2.2 应用

增量投入产出表可以用来计算经济增长中的软投入贡献(包括产出增长直接贡献和间接贡献、经济增长中软投入组合的完全贡献及各投入要素节约量占软投入贡献的比例等),分析经济增长方式转变及产业结构变化状况(包括产业关联分析及部门偏差分析)。

如本例关注2005—2010年间全国产业结构变化状况,可利用2005年(可比价)、2010年投入产出表计算出2005—2010年全国4部门的影响力系数和感应度系数进行产业关联分析;结合增量投入产出表,计算出2005—2010年各部门总产出增量及分别由最终需求、软投入组合引起的总产出变化量进行产业部门结构变化影响因素分析;通过产业结构偏差模型计算出2005—2010年全国各部门总产出偏差及最终需求、净出口、软投入组合变化引起的总产出偏差进行经济增长状况、产业结构与部门发展状况分析。最后,综合三者结果得出结论。

3 结语

多年的编制实践和探索显示,基于相同基础数据和部门合并编制出的增量投入产出表经常会出现不同结果,无据可依制约着增量投入产出表编制的准确性和认可度。本文在阐述增量投入产出表表式的基础上,重点研究增量投入产出表的一般性编制方法。研究发现,增量投入产出表的编制要点在于目标期投入产出表各对应调价系数的选取和确定及其可比价变换过程中的行列平衡调整。本文建议,在调价系数的选取和确定过程中,把逐项确定作为调价系数的选取方法;在平衡行列过程中,以“总产出”为准,利用减法得到初始投入,通过动态分摊法调整“总投入”。可比价变换在新表行列平衡后彻底完成。可以确定,若按本文所述编表,在基础数据、部门合并及调价系数确定方法相同的情况下,其编制结果将不会再有显著出入,利于增量投入产出表的后续推广和应用。

[1]李国璋.软投入及产出数量分析[M].甘肃:甘肃科学技术出版社, 1995.

[2]武玉洁.增量投入产出表:方法及应用[D].兰州:兰州大学经济学院,2008.

[3]闫来旗.1997一2002、2002一2007年中国增量投入产出表编制及软投入贡献测算[D].兰州:兰州大学经济学院,2011.

[4]陈南旭.甘肃省2002一2007年增量投入产出表的编制与应用[D].兰州:兰州大学经济学院,2012.

[5]陈宏伟.软投入与区域经济增长质量[D].兰州:兰州大学经济学院, 2010.

[6]张唯实.软投入与中国区域经济发展比较研究[D].兰州:兰州大学经济学院,2012.

[7]戚磊.产业关联、资本产出率与软投入贡献[D].兰州:兰州大学经济学院,2012.

[8]张伟,潘文卿.一个可比价投入产出表编制中价格指数求解的理论模型[J].甘肃社会科学,2003,(04).

[9]李强,薛天栋.中国经济发展部门分析——兼新编可比价投入产出序列表[M].北京:中国统计出版社,1998.

[10]刘起运,彭志龙.中国1992—2005年可比价投入产出序列表及分析[M].北京:中国统计出版社,2010.

(责任编辑/易永生)

C81