Lee-Carter模型外推预测死亡率及偏差纠正
2016-11-28吴晓坤李姚洁
吴晓坤,李姚洁
(华北电力大学数理学院,河北保定071003)
Lee-Carter模型外推预测死亡率及偏差纠正
吴晓坤,李姚洁
(华北电力大学数理学院,河北保定071003)
Lee一Carter模型是人口死亡率预测的常用模型,泊松最大似然估计法是该模型参数估计广为采纳的方法,模型中与时间相关的因子可建立时间序列模型并进行外推,进而实现死亡率的预测。由于时间因子与死亡率之间的非线性性,简单的外推会带来死亡率预测的低估偏差。这个偏差可以通过对数正态分布的性质进行纠正或者随机模拟方法进行无偏预测。
Lee一Carter模型;死亡率预测;对数正态分布;随机模拟;偏差
0 引言
Lee和Carter(1992)[1]提出的形式简洁、适用广泛的死亡率模型:

称为Lee-Carter模型。在Lee和Carter(1992)[1]后有很多学者对其进行了改进与完善,现在已经成为世界各国预测死亡率的常用模型。国内的很多研究者也将Lee-Carter模型用于中国人口死亡率的预测[2-5]。
国内外很多的研究与应用在利用人口数据建立模型并估计其中的未知参数后,利用指数↔对数互为逆变换的性质得死亡率本身的预测,这对变换在确定性数值间运算是正确的,但是在随机情形下却并不合适,将产生系统性的预测偏差。
1 参数估计
在形如式(1)的Lee-Carter模型中X表示X岁,t表示t时期,μx(t)为t时期X岁的死亡力,建模时常直接使用中心死亡率mx(t),mx(t)=dxt/e trxt,其中dxt为死亡人数,e trxt为平均年中人口数;αx为特定年龄x的总体死亡率因子; βx为年龄别x的死亡率变化因子,度量x岁人的死亡率随时间的变化强度;κt为时间因子,度量t时期所有年龄死亡率的改善水平;εxt为误差项。
本文利用《中国人口统计年鉴》和《中国人口和就业统计年鉴》提供的数据,整理出从1994年到2010年中国人口分年龄性别的死亡数据,年龄组从0岁(每一年龄一组)到90岁以上组。依据这些基础数据建立中国人口死亡率Lee-Carter模型,估计方法采用泊松最大似然方法。由于模型参数众多,并呈非线性关系,这里采用牛顿-拉夫逊算法(具体估计与计算方法可见于(Pitacco,Denuit和Haberman etal)[6]),并借助统计软件R实现。
利用最大似然方法估计参数首先要设定死亡人数的分布,本文假定死亡人数服从泊松分布,这是最为常见的一种假定,在此设定下参数的对数似然函数为:

其中,λxt=erxtexp(αx+βxκt)。根据最大似然估计原理与牛顿-拉夫逊算法,参数的最大似然估计迭代算法为:

其中,θ(i)代表参数θ的第i步的迭代值,θ(i)可以是似然函数中的任意参数或参数向量。在本文的问题中,令,代入具体的参数得参数的最大似然估计迭代算法,可以参考Pitacco,Denuit和Haberman et al[6]:

每一步计算后都要对参数进行调整,以确保所估计参数具有可识别性:

参数估计的结果如图1和图2所示。
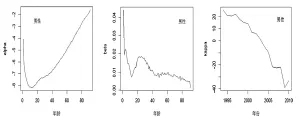
图1 男性模型参数估计

图2 女性模型参数估计
2 简单外推预测
模型参数中κt是死亡率中与时间相关部分,在观测时期t1,t2,...,tn,对应的参数κt的估计值构成一个时间序列,建立时间序列ARIMA模型,则可以根据模型对未来的κt进行预测。Lee和Carter(1992)[1]以及之后的许多研究者发现带漂移项的随机游走适合序列κt的建模,即:
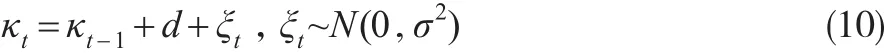
这里d为漂移项,ξt~N(0,σ2)为误差项,服从均值为0、方差为σ2的正态分布。
对κt的估计值建立时间序列模型并进行外推预测,可以得到:
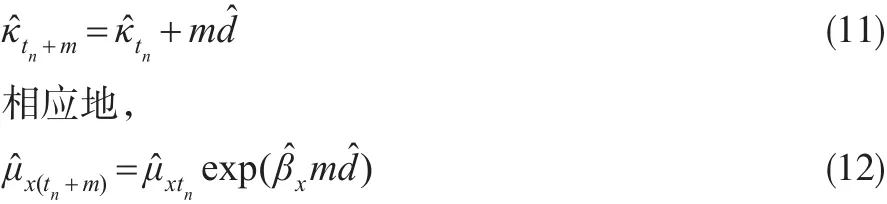
3 无偏外推预测
简单外推预测之所以存在偏差是因为死亡率与时间序列因子κt之间的非线性关系。由于它们之间的非线性关系,导致无法由κt的无偏估计经简单的κt与μxtn之间的函数关系得到死亡率μxtn,μx(tn+m)等的无偏估计。这是因为:
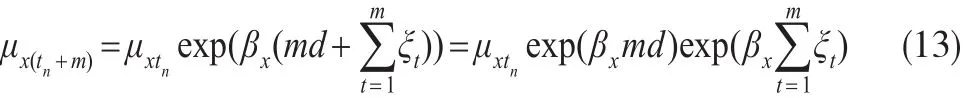
如果μxtn为已知数,则式(13)服从参数为(lnμxtn+的对数正态分布。其均值为:

可以用

来估计tn+m时的死亡率,ˆ与一般可以为d与σ2无偏估计,其中:

估计式(15)与式(12)明显的区别在于式(15)包含随
机误差项ξt的方差,而式(15)是根据死亡率的统计分布的均值式(14)得到的,所以具有无偏性。而式(12)是有系统偏差的,即使μxtn为常数,式(12)仍然有偏差。对于未来tn+m时的死亡率的预测,本文建议使用不存在系统偏差的式(15)。
本文比较了有偏差预测与无偏差预测,其结果详见图3与图4。这里分别使用式(12)与式(15)对2020年的死亡率进行预测,以对数形式及真实值形式进行结果比较。图3为男性的预测结果,其中的点线代表的是有偏差的式(12)的预测结果,从图形中可以看出预测结果偏低。相应的对于以上两种预测的出生整值预期寿命分别为76.77与77.04,带系统偏差的预测要高出无偏预测大约0.27岁。

图3 预测2020年男性死亡率

图4 预测2020年女性死亡率
对于女性,相应的预测结果是类似的,只是偏差更小一些。两种预测方法下,出生整值预期寿命分别为81.76与81.85,相差大约0.09岁。不管是男性还是女性,总的来说,带系统偏差的预测会低估死亡率,这在养老金领域的预测中经常被忽视,因为低估死亡率会增加预期寿命,会使人们面对老年危机的时候更加谨慎。然而,死亡率预测并不是仅仅供养老保险领域应用,所以有必要对预测的偏差进行纠正。
根据前面表达式可以对未来任意年份的死亡率进行预测,在此不再一一给出结果。
不管是男性还是女性,从图3和图4直观上看,带系统偏差的预测低估的死亡率并不明显,这可能也是具有系统性偏差预测能够被接受的一个原因。其实不然,这是因为死亡率本身在绝大多数年龄都很小,所以造成了这样的感觉。在下文中给出另一种无偏预测方法的同时采用另一种度量差异的方式来比较不同预测的不同,就可以看出其中明显的差异。
4 随机模拟预测的无偏性
另外一种得到无偏估计的方法是随机模拟法,利用计算机随机模拟技术不但可以得到死亡率的均值,当模拟次数足够大时可以认为模拟所得到的死亡率的随机样本的分布为死亡率总体的分布。根据式(13),如果有了μxtn或者其估计值,利用估计的βx和d值,每模拟一个ξt就会得到一个μx(tn+m),只要模拟的次数足够大,就可以利用模拟得到的所有μx(tn+m)值的平均值代替它的理论均值。这种方法思路简单易懂,其中复杂的模拟计算过程由计算机完成。在具体的模拟过程中在式(13)中取m值为10(这样可以预测得到2020年的死亡率,类似的,取不同的m值可以得到其它任意年份的死亡率);βx与d需要把数据代入模型根据最大似然估计算法和外推算法(式(4)—式(9)和式(16))进行估计得到中的σ2也需要估计得到(式(16))。首先模拟产生正态变量每产生一个模拟值代入式(13)就可以得到一个模拟的预测值,为了保证最后结果的稳定性,一般需要模拟的次数很大,比如1万次、10万次等。最终对模拟值求平均就得到所随机模拟预测的死亡率。在模拟次数很大时,模拟结果与无偏估计式计算所得结果非常接近。这里不再与简单估计结果进行直接的比较,本文计算了模拟预测与简单预测之差,同时也计算了进行纠正的无偏预测与简单预测之差,这两个差值本文称之为低估量;另外也分别计算了这两个低估量与纠正的无偏预测和模拟预测之比,本文称之为相对低估量。结果详见图5和图6。
从图5左图中可以看出男性人口死亡率预测中简单预测在高龄组会低估死亡率0.001到0.002,在0岁低估量接近0.001,其余低估量低于0.001;从图5右图中可以看出低龄组(0~10岁)的低估死亡率百分比在15%~5%之间,在10~30岁左右和60岁以上低估量百分比大约在2%~5%之间,其余年龄低估百分比较低。虽然简单外推预测的绝对低估量不高,最大0.002左右,尤其在0岁外的低龄组更是非常接近于0,但是从相对低估量来看则是低龄组偏高,最高可达15%。因为死亡率本身的绝对水平很低,所以绝对低估量也很低,但高达5%~15%的相对低估偏差却是不能忽视的。

图5 预测2020年男性死亡率偏差比较

图6 预测2020年女性死亡率偏差比较
图6 是女性预测结果,由于女性死亡率比男性更低一些,在绝对偏差图中所显示偏差为真实偏差的10倍。女性死亡率预测中定性的结果与男性类似,只是不管是绝对量还是相对量都低于男性,但相对低估量在一些年龄仍可高达6%,大多数年龄在2%左右。因此我们应该纠正简单外推的低估偏差。
5 总结
利用人口统计数据建立Lee-Carter死亡率模型后,在利用模型进行死亡率的单值预测时,常用的简单外推预测存在系统的低估偏差。这个偏差可以通过对数正态分布的性质或者运用随机模拟的方法进行纠正。通过理论分析与模拟计算发现:死亡率本身的值很小导致低估量的绝对值很小,但是相对量却不容忽视。因此建议利用Lee-Carter模型进行死亡率的单值预测时使用纠正的无偏预测或模拟预测。
[1]Lee R D,Carter L R.Modeling and Forecasting USMortality[J].Journalof the American Statistical Association,1992,87(419).
[2]韩猛,王晓军.Lee一Carter模型在中国城市人口死亡率预测中的应用与改进[J].保险研究,2010,(10).
[3]李志生,刘恒甲.Lee一Carter死亡率模型的估计与应用——基于中国人口数据的分析[J].中国人口科学,2010,(3).
[4]卢仿先,尹莎.Lee一Carter方法在预测中国人口死亡率中的应用[J].保险职业学院学报,2005,(6).
[5]王晓军,黄顺林.中国人口死亡率随机预测模型的比较与选择[J].人口与经济,2011,(1).
[6]Pitacco E,DenuitM,Haberman S,etal.Modelling Longevity Dynamics for Pensions and Annuity Business[M].UK:Oxford University Press,2009.
(责任编辑/易永生)
C921
A
1002-6487(2016)20-0019-03
国家社会科学基金重大项目(13&ZD164);教育部人文社科青年基金资助项目(15y JCZH186);中央高校基本科研业务费专项资金资助项目(2014MS163;2014ZD47);河北省社会科学基金资助项目(HB15LJ005)
吴晓坤(1978—),男,河北滦南人,博士,讲师,研究方向:统计与保险精算。
