认识方法用好方法——《有理数》中的数学方法

丁建生

认识方法用好方法——《有理数》中的数学方法

丁建生

有理数的学习帮助同学们扩充了数的范围,开拓了知识视野.在数学学习的过程中,同学们不仅要学好课本中的知识,还要善于发现、认识、提炼其隐含的数学思想方法.只有掌握了数学方法,才能体会数学的奥妙、领会数学的精髓.下面,结合例题谈谈《有理数》中的主要数学方法.

一、数形结合

数形结合是指将数(量)与(图)形结合起来,分析、研究、解决问题的一种思想方法.著名的数学家华罗庚说过:“数缺形时少直观,形缺数时难入微.”用数轴上的点表示有理数,就是简单的数形结合的体现.利用数形结合,可使复杂问题简单化,抽象问题具体化.

例1已知a＞0,b＜0,a+b＞0,试比较-a、a、-b、b的大小.

【解析】因为a＞0,b＜0,所以a在原点的右边,b在原点的左边.又因为a+b＞0,所以a的绝对值大于b的绝对值,即a离原点的距离比b远,由此a、b在数轴上的位置可表示出来.再根据相反数的意义,可把-a、-b在数轴上表示出来,所以,根据数轴上的点,左边的点所表示的数总比右边的点所表示的数小,可得出-a＜b＜-b＜a.

【反思】用数轴来比较数的大小是一种常用的有效方法.当然,本题若改为填空题,解答时可用特殊值法,如取a=2、b=-1,则-a=-2、-b=1,显然-2＜-1＜1＜2,即有-a＜b＜-b＜a.

例2同学们都知道，||5-（-2）表示5与-2之差的绝对值，实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.试探索：

(1)求||5-（-2）=.

(3)由以上探索猜想：对于任何有理数x,||x-3+||x-6是否有最小值?如果有，求出最小值；如果没有，说明理由.

【解析】(1)7;(2)画出数轴:

若设该数轴上表示-5与2的两个点是A、B,线段AB上任何一点为P,显然PA+PB= AB,故-5到2之间的所有数都满足||x+5+,其中,这样的整数有-5、-4、-3、-2、 -1、0、1、2.

(3)猜想:||x-3+||x-6有最小值3.由(2)不难看出,当x在3到6之间时,x到3的距离与x到6的距离的和是3,并且是最小的.当x＜3和x＞6时,x到3的距离与x到6的距离的和都大于3.

【反思】本题用了一个基本常识:

如图,直线上有三点A、B、P,若P在AB之间(含A、B),则PA+PB=AB;若P不在AB间,则PA+PB＞AB.

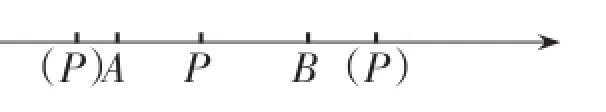
(事实上，此时PA+PB=2PA+AB或PA+ PB=2PB+AB).

用此结论,还可解决下列问题:

(1)求||x+1+||x-3+||x-6的最小值.

【提示】根据绝对值的意义,式子可看作是在数轴上x代表的点到数-1、3、6表示的点的距离之和,只有x=3时,式子有最小值7.

(2)求||x+2+||x+1+||x-3+||x-6的最小值.

【提示】在数轴上画出表示-2、-1、3、6的点A、B、C、D,若表示数x的点为P,式子就是点P到点A、B、C、D的距离之和,显然只有当P在BC间(含B、C)时,有最小值为PB+ PC+PA+PD=BC+AD.

(3)如图,某冰箱厂的生产流水线上依次排列着A、B、C、D、E五名工人在组装零部件,现欲设一个零件供应点,问:设于何处,可使五名工人与零件供应站的距离总和最小?如果有6名工人又该怎样呢?如果有n名工人时,零件供应站应设在何处?

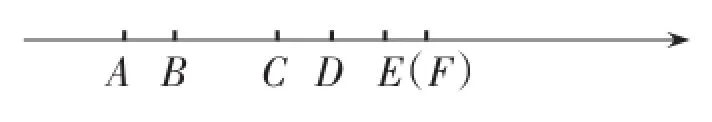
【提示】五名工人时,设在C处.此时,总距离为AE+BD;若6名工人,供应点设在第3和第4名工人之间;当n为奇数时,供应点应设在第个点处,若n是偶数,供应点应设在第+1个点之间的任一点上.

二、分类讨论

在解答某些数学问题时,有时会遇到多种情况,需要对各种情况加以分类,并逐类求解,然后综合得解,这就是分类讨论法.分类必须做到:每一次分类要按照同一标准进行;分类要做到不重复、不遗漏.

例3比较3a和-3a的大小.

【解析】由于题中没有给出a的取值范围,故需分三种情况来进行讨论: (1)当a＞0时,3a＞0,-3a＜0,∴3a＞-3a; (2)当a=0时,3a=0,-3a=0,∴3a=-3a; (3)当a＜0时,3a＜0,-3a＞0,∴3a＜-3a.【反思】解本题时,应首先想到a=0时, 3a=-3a,再想到a＜0、a＞0.

a＜-1;a=-1;-1＜a＜0;0＜a＜1;a=1; a＞1.

例4已知||x=3,y2=16,xy＜0,求x-y的值.

【解析】由||x=3,得x=3或-3;由y2=16,可得y=4或-4,再由xy＜0,可知x、y异号,故分两种情况:当x=3、y=-4时,x-y=3-（-4）=7;当x=-3、y=4时,x-y=-3-4=-7.

【反思】本题若没有xy＜0,就要分四种情况.

【解析】因为||a-b+||c-a=1,并且a、b、c均为整数,所以||a-b和||c-a=0或1,当||a-b=1时,||c-a=0,则c=a,||c-b=1,时,||c-a=1,则b=a,||c-b=1,||a-c+

【反思】本题中条件——“整数”是非常重要的,如果把题目中的条件||a-b+,其他不变,你会解吗?

例6一个正方体的每个面分别标有数字1，2，3，4，5，6.根据下图中该正方体三种状态所显示的数据，能否推出“?”处的数字是多少?

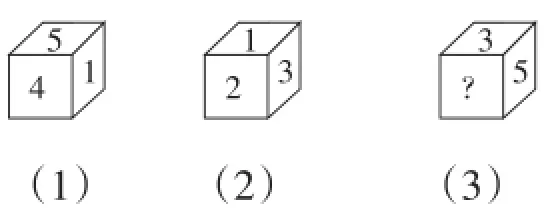
【解析】本题可先尝试确定每个面的数.根据图(1),设与数1相对的面上的数是a,与数4、5相对的面上的数分别是b、c.显然a、b、c只能在数2、3、6中取.下面分情况讨论:当a=2时,这与图(2)中数1、2相邻相矛盾;当a=3时,同样与数1、3相邻相矛盾.故a=6.当b=2时,则c=3,这与图(3)中数3、5相邻矛盾.故只有b=3,c=2.所以a=6,b=3,c=2.这样“?”处的数是6.

【反思】本题实际上进行了多级分类,把各种情况一一列举(讨论),“不重复、不遗漏”,才正确地找出了符合要求的答案.

三、化归转化

化归转化,就是将所要解决的问题化为已经学过的老问题加以处理的一种方法.如,利用相反数的概念,将有理数的减法转化成有理数的加法,即“减去一个数等于加上这个数的相反数”.转化,就是把“新知识”转化为“旧知识”,把“未知”转化为“已知”,把“复杂”转化为“简单”,把“陌生”转化为“熟悉”.

例7计算：1+2-3-4+5+6-7-8+9+10-11-12+…+2013+2014-2015-2016.

【解析】若逐一计算会很麻烦,经过观察,发现数值的绝对值是连续整数,运算符号四个为一组循环,而2016能被4整除.于是把这4个一组的数作为一个整体,问题就迎刃而解了.

原式=(1+2-3-4)+(5+6-7-8)+(9+10-11-12)+…+(2013+2014-2015-2016) =(-4)+(-4)+(-4)+……+(-4)=(-4)×504 =-2016.

【反思】此题中将每四个数进行组合,从而2016个数的加减运算就转化成为504个数(相同)的加法运算,这是由复杂向简单转化的过程.

例8现有37只茶杯整齐地放在桌上，且都是杯口朝下，现在每次把任意6个茶杯倒置过来(不论原来杯口是朝上还是朝下)，能否经过若干次后，使所有的茶杯的杯口都朝上，如果能够做到的话，请你设计一种方案，如果不能做到，请你说明理由.

【解析】不可能.假设每个杯杯口朝下记为+1,则37个杯杯口朝下即37个(+1)相乘仍得+1,一次倒置6个茶杯就相当于把每个杯子乘以-1,6个(-1)相乘得+1,而最后要求37个杯杯口朝上,即37个(-1)相乘,此时结果得-1,而+1不论怎么乘以若干个(+1)都不可能变成-1.所以,不可能经过若干次变化,使37个杯子杯口都朝下.

【反思】本题中的数字37较大,用列举法几乎行不通!这就需要我们想出能揭示其本质的东西(方法),当我们用+1、-1表示其状态时,问题就变得简洁、明了.这是将实际问题转化成纯数学(数字)问题(有理数运算)的过程.同学们有没有体会到数学的魅力?

江苏省南京师范大学第二附属初级中学)