考虑松动圈影响的引水隧洞应力及位移弹性分析

张 晓 驰

(新华水力发电有限公司，北京 100070)



考虑松动圈影响的引水隧洞应力及位移弹性分析

张 晓 驰

(新华水力发电有限公司，北京 100070)

采用弹性力学理论，推导出圆形隧洞衬砌和围岩松动圈的应力及位移解析解，并以新疆某引水隧洞工程为背景，分析了平面应变、弹性情况下，衬砌及松动圈支护体内应力之差与位移分布规律，最终得出了一些有价值的结论。

隧洞，松动圈，应力，位移

0 引言

引水隧洞是水利水电建设领域中一种常见的工程结构形式，特别是在水利工程的输调水工程中发挥着重要的作用，其衬砌及围岩的稳定性直接影响到整个工程设计及施工管理，因而围岩及稳定性评价具有十分重要的现实意义[1,2]。

在很多隧洞工程中，衬砌设计会综合考虑围岩松动圈的影响，并运用松动圈支护理论对衬砌支护进行设计修正，以使得衬砌设计更符合现场实际，但通过调研发现，目前研究大多都基于工程经验，缺乏在理论上的进一步探讨[3,4]。

本文考虑引水隧洞围岩松动圈的影响，推导出圆形隧洞衬砌和围岩松动圈的应力及位移解析解，并分析了衬砌及松动圈支护体内切向应力与径向应力之差、位移沿径向的分布规律。研究方法和结论希望能为类似工程提供借鉴。

1 圆形引水隧洞应力及位移分析

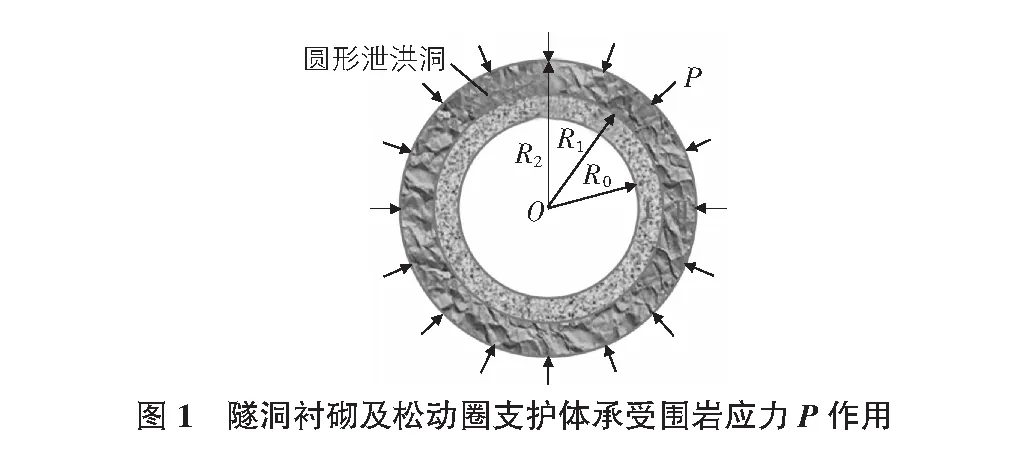
假设围岩松动圈和衬砌支护时机恰到好处，使得松动圈支护体和衬砌完全接触，共同承受围岩的均布应力P作用。如图1所示，Ⅰ层为钢筋混凝土衬砌，Ⅱ层为围岩松动圈支护体。隧洞衬砌及围岩松动圈支护体的半径从内到外依次为R0，R1，R2；泊松比依次为μ1，μ2；弹性模量依次为E1，E2。

由于圆形隧洞是轴对称问题，因此在平面应变弹性情况下，衬砌及围岩松动圈支护体的应力及位移求解如下[5,6]：

几何方程：

(1)

平衡方程：

(2)

应变表示的相容方程：

(3)

弹性阶段本构方程：

(4)

联合式(1)～式(4)，轴对称问题的应力分量形式即可求得[7,8]:

第Ⅰ层，钢筋混凝土衬砌内应力分量：

(5)

第Ⅱ层，围岩松动圈支护体内应力分量：

(6)

文中以压为正，σθ>σρ>0，设定轴向荷载σz按式(7)取值[7]：

(7)

其中平面应变模型下，mi=2μi，对于Ⅰ,Ⅱ层，i分别取值1，2。

将应力分量表达式代入基本方程可得内外层衬砌的径向位移解[7,8]：

第Ⅰ层，钢筋混凝土衬砌内位移分量：

(8)

第Ⅱ层，围岩松动圈支护体内位移分量：

(9)

应力及位移边界条件如下：

衬砌内边界(ρ=R0)，σρ1=0;衬砌与松动圈支护体交界面(ρ=R1)，σρ1=σρ2，V1=V2;围岩松动圈支护体外边界(ρ=R2)，σρ2=P。

(10)

(11)

(12)

(13)

根据式(10)～式(13)可解得Xi，Yi(i=1,2)。

(14)

(15)

(16)

(17)

2 算例求解与分析

新疆某水电站工程区段隧洞围岩为元古界埃连卡特组(Pta)变质岩系，洞室内一般无地下水影响，岩石新鲜完整，片理面结合紧密。圆形断面，洞径7.2 m，钢筋混凝土衬砌，衬厚0.8 m，经现场测试，围岩松动圈厚度1.0 m。取衬砌的泊松比μ1=0.2，弹性模量E1=30 GPa,围岩松动圈支护体的泊松比μ2=0.25，弹性模量E2=35 GPa。将相关参数数值代入所求的位移解析解中可得引水隧洞的衬砌及围岩松动圈支护体内的切向应力与径向应力之差、位移沿径向的分布规律。

弹性分析下，文中只讨论衬砌及围岩松动圈支护体内的应力之差、位移的分布规律，故而首先将计算结果进行归一化处理，如

图2所示。从图2可以看出，两层结构内的位移呈现连续分布，且随着半径的增大而增大，并在松动圈支护体最外层处出现最大值。而两层结构内的应力差呈现不连续分布，在衬砌与围岩松动圈支护体的交界面处出现中断，即在每层结构的内壁处都取最大值，出现了切向应力集中。由强度理论知，最大主应力与最小主应力差值的大小决定了材料的破坏，所以在实际工程中应对衬砌与围岩松动圈支护体的内壁处加以重视。

3 结语

1)根据弹性力学理论，推导出圆形隧洞衬砌和围岩松动圈的应力及位移解析解，并以新疆某引水隧洞工程为背景，在平面应变、弹性情况下，分析了衬砌及松动圈支护体内切向应力与径向应力之差、位移沿径向的分布规律。2)将结构内应力差、位移的计算结果进行归一化处理，得出两层结构内的位移呈现连续分布，且随着半径的增大而增大，并在松动圈支护体最外层处出现最大值。而两层结构内的应力差呈现不连续分布，在衬砌与围岩松动圈支护体的交界面处出现中断，即在每层结构的内壁处都取最大值，出现了切向应力集中。

[1] 陈卫忠,伍国军,戴永浩,等.锦屏二级水电站深埋引水隧洞稳定性研究[J].岩土工程学报,2008,30(8):1184-1190.

[2] 吴世勇,任旭华,陈祥荣,等.锦屏二级水电站引水隧洞围岩稳定分析及支护设计[J].岩石力学与工程学报,2005,24(20):3777-3782.

[3] 王世夏.水工设计的理论和方法[M].北京：中国水利水电出版社,2000.

[4] 师金锋,张应龙.超大断面隧道围岩的稳定性分析[J].地下空间与工程学报,2005,1(2):227-230.

[5] 徐芝纶.弹性力学简明教程[M].北京:高等教育出版社,2002.

[6] 杨桂通.弹塑性力学引论[M].第2版.北京：清华大学出版社,2013.

[7] 李建春,张永强,俞茂宏.一个弹粘塑性问题的统一解析解[J].力学与实践,2000,22(1):31-34.

[8] 张常光,胡云世,赵均海,等.深埋圆形水工隧洞弹塑性应力和位移统一解[J].岩土工程学报,2010,32(11):1738-1745.

On water-diversion tunnel stress and displacement elastic analysis with consideration of broken rock zones

Zhang Xiaochi

(XinhuaHydropowerCompanyLimited,Beijing100070,China)

The paper adopts the elastic dynamic theory, induces the stress and displacement analytical solution of the circular tunnel lining and broken rock zones of surrounding rock, based on some water-diversion tunnel in Xinjiang, analyzes the distribution law of the lining and inner stress of the broken rock zones under the plane stress and elastic circumstances, and achieves the valuable conclusion.

tunnel, broken rock zone, stress, displacement

1009-6825(2016)13-0174-02

2016-02-24

张晓驰(1982- )，女，硕士，工程师

U451

A