刚性连接及在结构分析中的应用

王 静 王安山

(1.北京迈达斯技术有限公司，北京 100044； 2.交通运输部公路科学研究院，北京 100088)



刚性连接及在结构分析中的应用

王 静1王安山2

(1.北京迈达斯技术有限公司，北京 100044； 2.交通运输部公路科学研究院，北京 100088)

结合刚性连接的基本原理，阐述了不同单元连接自由度不协调时，运用刚性连接使单元间的自由度实现变形协调的方法，并基于midas Gen软件进行了分析计算，指出采用刚性连接可以有效解决结构变形协调的问题。

刚性连接，节点耦合，自由度协调，midas Gen

1 概述

运用有限元进行结构分析，边界条件的模拟至关重要，合适的边界模拟也是工程中的难题之一。刚性连接是最常用的边界条件之一，刚性连接就是通过节点间自由度的耦合，建立变形协调方程。刚性连接在结构分析中的应用十分广泛，最常用的形式是模拟刚臂、刚性隔板假定。当不同单元连接时，可能自由度不相同，刚性连接就是最有效进行变形协调的手段之一，对于分析软件而言，可以在不修改内核的前提下，实现很多特殊的计算需求。

本文算例采用midas Gen 8.36进行分析。

2 刚性连接

2.1 基本概念

刚性连接[1]是强制某些节点(从属节点，Slaver)的自由度从属于某节点(主节点，Master)，其作用原理是通过约束节点之间的相对几何变形，增加位移约束平衡方程。使用刚性连接时，节点自由度的耦合关系不能重复。

刚性连接一般形式见图1。

2.2 自由度耦合的一般形式

令从属节点和主节点的6个自由度(Dx，Dy，Dz，Rx，Ry，Rz)全部耦合，即主从节点进行三维刚体连接。则主节点与从属节点之间的位移约束方程为：

(1)

其中，dx,dy,dz分别为变形前主节点和从属节点的距离在整体坐标系x，y，z轴上的投影。

(2)

其中，xm,ym,zm均为主节点的坐标；xs,ys,zs均为从属节点的坐标；Ux,Uy,Uz,Rx,Ry,Rz分别为节点在整体坐标系中沿x,y,z轴方向的位移和绕x,y,z轴的转角；下标m为主节点(Master)；下标s为从属节点(Slaver)。

3 刚臂模拟

根据上述刚性连接的基本原理，可以采用刚性连接来实现刚臂的效果。模型示意图见图2，位移图Dz见图3。

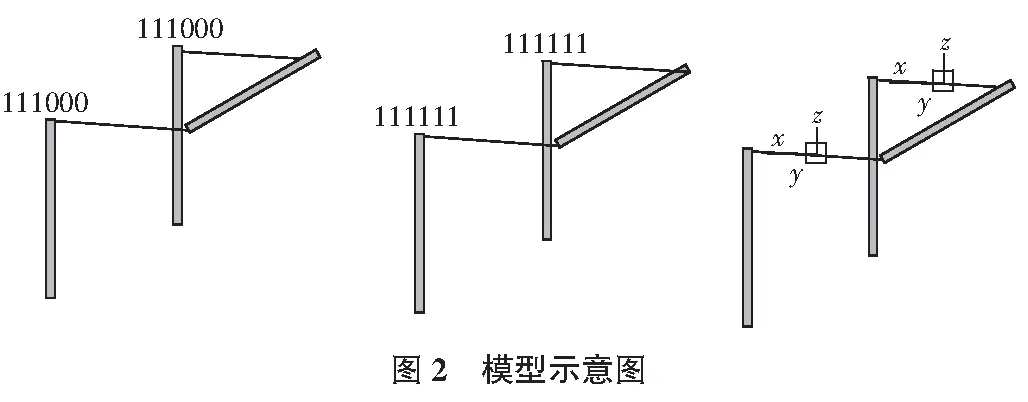
模型1，采用刚性连接，只约束三个平动自由度(Dx，Dy，Dz)，主节点和从节点的z向位移差完全相同。

模型2，采用刚性连接，三个平动自由度(Dx，Dy，Dz)和三个扭转自由度(Rz，Ru，Rz)全部耦合，主节点和从节点的z向位移差约604 mm。尽管约束了z向的自由度，由于两节点的x向距离较大，绕y轴的转角产生的竖向位移占主要成分。

模型3，采用弹性连接的“刚性”，即增加“刚臂”，两节点的竖向位移差约604 mm，和模型2的结果完全相同。模型主要参数及位移结果见表1。

表1 模型主要参数及位移结果

可见，两节点间6个自由度全部耦合时，和增加“刚臂”的效果完全等价，但刚性连接的形式更为灵活，且不会产生刚臂刚度设置过大，而导致分析异常。实际工程中，应根据具体情况进行使用。

4 刚性隔板假定

结构设计中常用的刚性隔板假定，就是基于刚性连接实现的，假定楼层标高处所有节点的Dx，Dy，Rz自由度从属于刚心。根据位移协调方程简化为：

(3)

利用刚性连接实现刚性楼板假定，在midas Gen中的工程展示见图4。

5 不同单元类型间的连接

梁单元的每个节点具有三个方向的平动自由度(Dx，Dy，Dz)和三个方向的旋转自由度(Rx，Ry，Rz)，板单元的每个节点具有三个方向的平动自由度(Dx，Dy，Dz)和绕面外的两个旋转自由度(Rx，Ry)，这种没有面内旋转自由度的单元互相连接时，节点处可能发生自由度奇异，midas Gen采用自动约束旋转自由度的方法解决了这一问题。

当板单元与具有旋转自由度的梁单元相连接时，仍采用自动旋转自由度的方法，虽然能产生梁端弯矩，但是引起的误差往往是不能忽略的，在通常的结构分析模型中，剪力墙用壳单元模拟，

框架梁用梁单元模拟，连梁也包括壳单元连梁和梁单元连梁。因此，有必要研究壳单元与梁单元的协同作用分析是否真实合理。

5.1 梁板连接算例

本文通过一片剪力墙顶悬挑一跨梁的简单模型进行分析研究，剪力墙尺寸2 m×8 m，厚度240 mm，墙面内方向外悬框架梁，悬挑跨度2 m，梁截面240 mm×600 mm，悬挑端部施加一竖直向下的节点力300 kN，不考虑结构自重，混凝土等级C30。采用midas Gen软件，共计7组模型进行对比分析，第1组悬挑梁、剪力墙全部采用壳单元(Shell)模拟，网格尺寸0.5 m，以此模型的结果作为对比参考值；第2～5组模型的悬挑梁采用梁单元(Beam)模拟，剪力墙采用壳单元模拟，按网格尺寸进行区分；第6～7组模型悬挑梁采用梁单元模拟，但悬挑梁根部增加刚性连接的定义。计算模型示意图见图5，主要模型信息见表2。

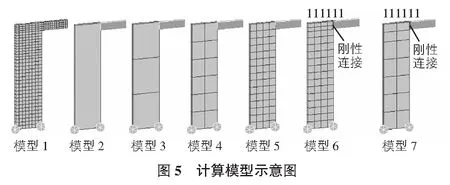
表2 模型主要参数

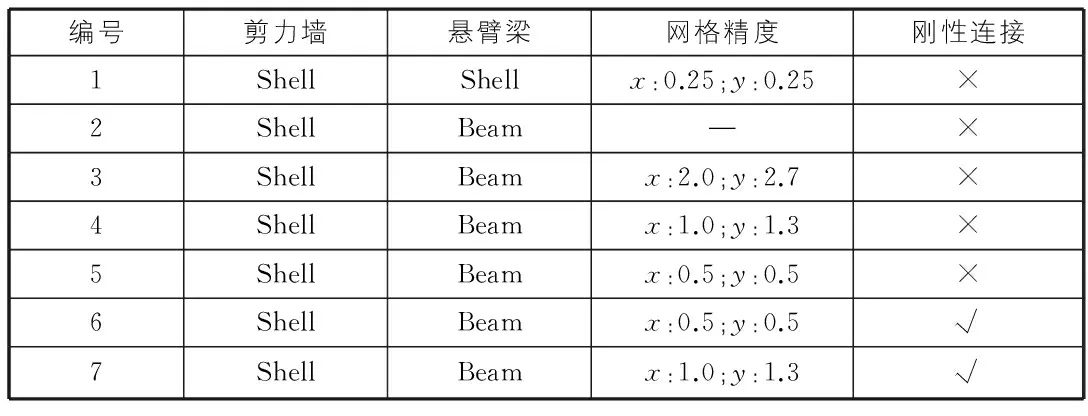
编号剪力墙悬臂梁网格精度刚性连接1ShellShellx:0.25;y:0.25×2ShellBeam—×3ShellBeamx:2.0;y:2.7×4ShellBeamx:1.0;y:1.3×5ShellBeamx:0.5;y:0.5×6ShellBeamx:0.5;y:0.5√7ShellBeamx:1.0;y:1.3√

计算结果见图6，通过悬挑梁的远端竖向位移和支座反力两个重要指标，分析各组模型分析结果的合理性。

5.2 结构位移

第1组模型的悬挑梁(壳单元)远端中点的竖向位移为15.176 mm，第2～5组模型悬挑梁采用梁单元，随着网格越来越密，变形越来越大。通常认为网格尺寸越小，结果越精确，但这里的结果与一般性结论恰恰相反，网格越小，越偏离真实解。对于第5组模型，网格尺寸为0.5 m时，梁远端竖向位移达到155.786 mm，已经完全失真。

可见依靠程序只约束连接节点的旋转自由度，并不能得到期望解，主要是因为梁单元简化为线单元进行分析，没有考虑梁高的影响。随着板单元网格尺寸越小，整块大板的面内旋转机动性越强，梁板连接节点的旋转变形越大，引起悬挑梁远端的竖向位移越大。

这里采用刚性连接，将梁高的影响考虑进去。而梁高范围内的板外侧节点从属于梁根部节点，当网格尺寸为0.5 m时，悬挑梁远端竖向位移为14.029 mm，误差7.56%；当网格尺寸为1.0 m时，悬挑梁远端竖向位移为13.214 mm，误差12.93%。悬挑梁端部位移结果对比见表3。

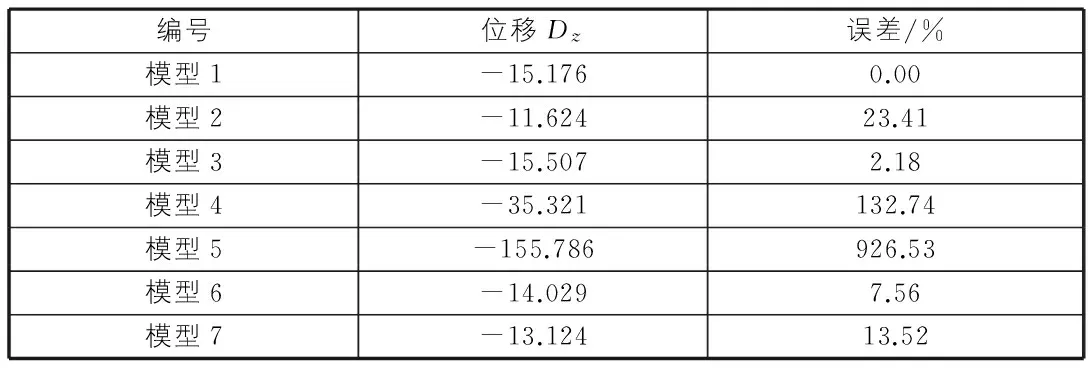
表3 悬挑梁端部位移结果对比

本算例为了突出问题的重要性，所取荷载较大，可以证明当荷载减小时，误差显著减小。实际工程中板(墙)网格大小一般取0.5 m～1.0 m，第7组模型的结果完全可以满足工程要求。

5.3 小结

通过以上7组模型对比分析，直接建立的梁板连接模型产生的误差不可忽略。通过刚性连接以考虑梁高的影响的模型，整体结果趋于稳定，与全壳单元精细模型的结果基本一致，对于工程常用的网格尺寸0.5 m～1.0 m，误差可以满足工程要求。可见，刚性连接是一种有效的解决不同单元间连接自由度不协调的方法。

6 结语

1)根据刚性连接的基本原理，当自由度全部耦合时，与“刚臂”效果完全等价。

2)当不同单元类型进行连接，节点自由度不相同时，采用刚性连接可以有效解决变形协调的问题，以保证分析结果的准确性。

3)工程常用的刚性隔板假定，当程序没有直接提供此功能时，可以采用刚性连接实现，理论完全一致。

结构分析中，很多变形协调和自由度耦合问题都可以采用刚性连接解决，但应在了解其基本原理的前提下合理使用。

[1] 北京迈达斯技术有限公司.Gen分析与设计原理[Z].2014.

[2] 肖奇志，蒋海云.刚性楼板假定的工作原理及其选用方法[J].中外建筑，2007(9):100-101.

Application of rigidity connection in structural analysis

Wang Jing1Wang Anshan2

(1.BeijingMaidasiTechnologyCo.,Ltd,Beijing100044,China;2.AcademyofHighwayScience,TheMinistryofTransportation,Beijing100088,China)

Combining with basic principles of rigidity connection, the paper describes the methods of applying rigidity connection to make inter-unit freedom deformation coordination when the inter-unit fails to freedom coordination, and carries out analysis and computation on the basis of midas Gen, and finally points out that: it can effectively solve structural deformation coordination problem by applying rigidity connection method.

rigidity connection, joint coupling, freedom coordination, midas Gen

1009-6825(2016)13-0045-03

2016-02-24

王 静(1984- )，女，工程师

TU311.41

A