发散型阶梯式磁流体密封的磁场有限元分析

杨小龙,陆文丽,孙康康,谌炎辉

(广西科技大学机械工程学院，广西柳州545006)

发散型阶梯式磁流体密封的磁场有限元分析

杨小龙,陆文丽,孙康康,谌炎辉

(广西科技大学机械工程学院，广西柳州545006)

阶梯式磁流体密封结构是一种在阶梯式迷宫密封基础上提出的用以提高普通磁流体密封耐压能力的新型密封结构.为了在阶梯式磁流体密封结构密封间隙内获得最大磁能积，在阶梯式磁流体密封理论的基础上，对一种具有二级磁源的发散型阶梯式磁流体密封结构进行了磁路设计，同时采用有限元法数值计算出密封间隙内的磁场分布从而计算出阶梯式磁流体密封耐压能力，并对计算结果进行了分析和讨论.结果表明:发散型阶梯式磁流体密封耐压能力随着径向密封间隙的增大而减小;永磁体与极靴结合处的漏磁是导致磁路法设计的发散型阶梯式磁流体密封结构耐压能力偏高的原因.

磁路;大间隙;磁流体;密封;数值计算

0 引言

磁流体密封技术因其具有零泄漏、寿命长和无污染等优点而广泛应用于航空航天、机械、石油和化工等领域中［1］.在要求大间隙的高速及重载等领域中，普通磁流体密封性能随着密封间隙的增大而显著减小［2］.阶梯式磁流体密封是一种在阶梯式迷宫密封基础上提出的用以提高普通磁流体密封耐压能力的新型密封结构.该结构是通过将阶梯式迷宫密封中的外壳改进为普通磁流体密封中的永磁体和极靴而形成的.与普通磁流体密封相比，阶梯式磁流体密封结构不仅有普通磁流体密封聚磁功能的径向密封间隙，还具有聚磁功能的轴向密封间隙.因此研究发散型阶梯式磁流体密封对于提高大间隙磁流体密封性能具有重要的意义.

磁路设计是阶梯式磁流体密封设计的关键.目前研究人员对磁流体密封的磁路设计、磁场有限元分析和耐压性能进行了大量的研究［3-10］，但对于阶梯式磁流体密封结构的研究报道较少.本文采用磁路设计法设计了发散型阶梯式磁性流体密封结构，并采用磁场有限元法对磁路法设计的密封结构进行了数值验证，从而为大间隙阶梯式磁流体密封设计提供依据.

1 发散型阶梯式磁流体密封理论及磁路设计

1.1 发散型阶梯式磁流体密封理论

发散型阶梯式磁流体密封理论耐压公式为:

式(1)中:Pjr和Pja为第j个极靴和阶梯轴形成的径向密封间隙和轴向密封间隙的耐压能力.如果Pjr小于Pja，λ为1，否则为0.Pjr和Pja可以通过方程式(2)计算得到.

轴向和径向密封间隙内普通磁流体密封理论耐压公式为［1，3，6］:

式(2)中:MS为磁流体饱和磁化强度分别为工作间隙内第i级极齿下磁通密度最大值和最小值;N为总的密封级数.从上式可以看出，阶梯式磁流体密封是利用阶梯轴与极靴形成径向轴向和径向密封间隙以提高阶梯式磁流体密封性能.

1.2 发散型阶梯式磁流体密封磁路设计

图1为具有二级磁源的发散型阶梯式磁流体密封结构，其等效磁路如图2所示.

图1 发散型阶梯式磁流体密封原理图Fig.1 Schematic diagram of diverging stepped magnetic fluid seal

图2 发散型阶梯式磁流体密封等效磁路图Fig.2 Equivalent magnetic circuit of diverging stepped magnetic fluid seal

根据永磁体退磁曲线及阶梯式磁流体密封结构磁路参数，可以计算出永磁体的长度和截面积，从而使得阶梯式磁流体密封间隙中有最大磁能积并提高永磁体利用率.

从图2可以看出，磁回路主要由极靴、磁流体、永磁体以及阶梯轴组成.永磁体为等效磁路的磁源，它产生的磁场将极靴和阶梯轴形成的径向和轴向间隙中的磁流体牢牢束缚在密封间隙内，磁流体产生抵抗密封结构两侧的压差的磁场力从而实现密封的目的.

在对阶梯式磁流体密封进行磁路设计时，包含2个假设:即忽略漏磁影响和忽略边缘效应影响.

根据磁路基尔霍夫第一定律有:

Φ1，Φ2和Φ3分别表示高压侧磁极、中间磁极和大气压侧磁极内的磁通量.其中:

由Φm1=Φ1可得:

其中，Φm1，Bm1和Sm1分别表示高压侧第1永磁体的磁通量、磁通密度和环形面积.

由Φm2=Φ3可得:

其中，Φm2，Bm2和Sm2分别表示大气压侧第2永磁体的磁通量、磁通密度和环形面积.

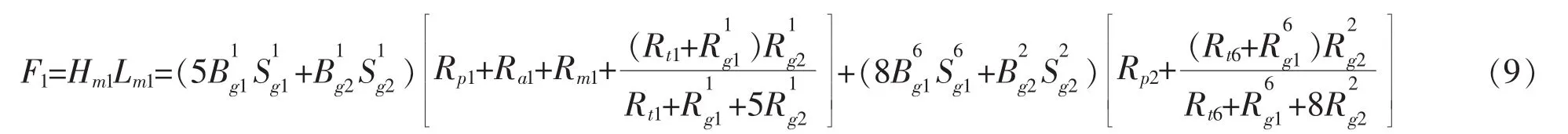
其中，F1表示高压侧永磁体的磁势;Hm1，Lm1表示第1永磁体的磁场强度以及长度和Rt1分别表示高压侧第1极靴、第1极靴的第1极齿下第1径向密封间隙、第1极靴轴向密封间隙、第1阶梯轴轴、第1永磁体和第1极齿的磁阻.分别表示第2极靴、第2极靴径第6极齿径向间隙、第2极靴轴向密封间隙和第6极齿的磁阻.

其中，F2表示大气压侧永磁体的磁势;Hm2，Lm2表示第2永磁体的磁场强度以及长度;Rp3，Ra2，Rm2，Rt14和分别表示第3极靴、第2阶梯轴、第2永磁体、第3极靴第14永极齿和第14极齿下径向密封间隙的磁阻.

又因为2块永磁体的形状、大小及其性能参数是相同的，则有:

式(15)乘以式(16)得:

式(15)除以式(16)得:

由于极靴和转轴材料的磁导率远大于空气和永磁体磁导率;因此，在计算永磁体长度时，阶梯轴、极靴和极齿的磁阻忽略不计，则有:

2 有限元分析

为了验证磁路法的可靠性，采用了如图1所示的具有双磁源结构的发散型阶梯式磁流体密封结构，密封结构的各部分参数如下:第1极靴的轴向长度、内半径和外半径分别为5 mm，16.6 mm和30 mm;第2极靴的轴向长度、内半径和外半径分别为8 mm，18.1 mm和30 mm;第3极靴的轴向长度、内半径和外半径分别为5 mm，19.6 mm和30 mm;轴向密封间隙宽度和径向密封间隙高度大小均为0.7 mm;第1，第2和第3极靴上的极齿数分别为5，8和5;齿槽宽和齿槽深分别为0.8 mm和0.7 mm.

在阶梯式磁流体密封磁路中，选用的永磁体为钕铁硼材料，其矫顽力为1.356×106A/m，磁导率为1.05.最大磁能积的工作位置即Hm和Bm分别为-0.678×106A/m和0.711 9×106A/m.第1至第3极靴选为电工纯铁材料，阶梯轴材料为2cr13不锈钢.磁流体为机油基磁流体，其饱和磁化强度为30 kA/m.若要求密封耐压能力不小于1.2个大气压，由发散型阶梯式磁流体密封理论可得其轴向和径向密封间隙内总磁感应强度差为4特斯拉，由阶梯式磁流体密封的磁路设计中式(17)、式(19)以及发散型阶梯式磁流体密封基本几何参数可得永磁体长度和横截面积分别为5.6 mm和243 mm2.由于永磁体的外径为30 mm;因此永磁体内径为24 mm.即永磁体工作在最大磁能积位置处的内径、外径和长度分别为24 mm，30 mm和5.6 mm.

在ANSYS有限元分析软件前处理器中创建阶梯式磁流体密封的物理环境.根据阶梯式磁流体密封结构对称性，阶梯式磁流体密封的三维轴对称问题可以简化为二维平面问题.由于阶梯式磁流体密封结构中密封间隙内永磁体产生的磁场强度远大于磁流体饱和磁化强度，所以磁流体被饱和磁化，其磁导率与空气的磁导率相差不大，可以将磁流体当作空气来处理.

根据发散型阶梯式磁流体密封的结构参数，建立该密封结构的二维模型.将永磁材料的矫顽力MGXX，MGYY，MGZZ分别设为0，1.356×106，0;0，-1.356×106，0.各零部件赋予相应材料属性后，智能网格划分，网格精度等级为3级.发散型阶梯式磁流体密封的二维模型的边界条件为磁力线平行，通过求解器进行求解.

3 分析结果及讨论

在ANSYS后处理器中沿着泄漏通道方向定义一条轨线，将计算出的磁场强度和磁通密度映射到该轨线上.轴向密封间隙高度为0.4 mm时，沿泄漏通道方向轨线磁场强度H和变化曲线如图3～图6所示.从图3～图6中可以看出，在其不同径向密封间隙中，阶梯式磁流体密封结构磁场强度最大值位于轴向密封间隙内，这是因为由安培环路定理可知，磁回路越短其磁场强度越大;又因为通过轴向密封间隙中的磁回路比通过径向密封间隙中磁回路要短;因此，导致轴向密封间隙内磁场强度大于径向密封间隙内磁场强度.当径向密封间隙的磁场强度小于轴向密封间隙内磁场强度时，径向密封间隙中磁流体密封性能低于轴向密封间隙中磁流体密封能力.从图3～图6中不难发现，随着径向密封间隙高度的增加，径向密封间隙内的磁场梯度场也越来越小，这是由通过轴向密封间隙内磁路较短以及径向密封间隙高度大于轴向密封间隙宽度造成的.

当轴向密封间隙高度为0.4 mm时，发散型阶梯式磁流体密封性能随着径向密封间隙高度变化曲线如图7所示.发散型阶梯式磁流体密封性能随着径向密封间隙高度增加而显著降低.这是因为由磁路定理和阶梯式磁流体密封耐压理论可知，径向密封间隙高度越大，其磁路的总磁阻也越大，这导致磁路中磁通量密度和磁场强度较小;因此，阶梯式磁流体密封的耐压能力显著下降.

图3 密封间隙为0.4 mm时磁场分布图Fig.3 Magnetic distribution in 0.4 mm sealing gap

图4 密封间隙为0.5 mm时磁场分布图Fig.4 Magnetic distribution in 0.5 mm sealing gap

图5 密封间隙为0.6 mm时磁场分布图Fig.5 Magnetic distribution in 0.6 mm sealing gap

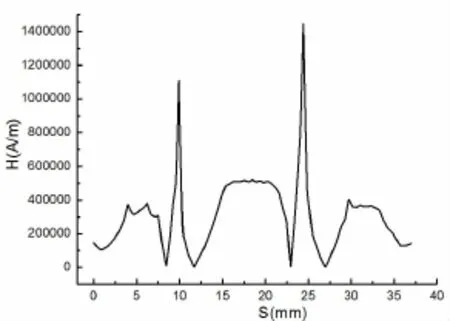
图6 密封间隙为0.7 mm时磁场分布图Fig.6 Magnetic distribution in 0.7 mm sealing gap

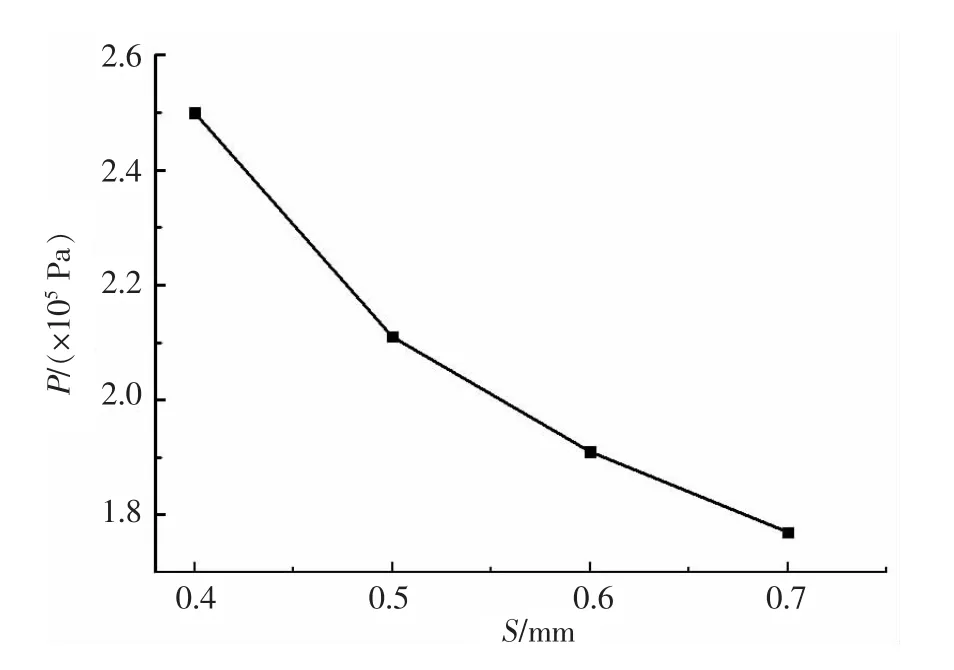
图7 径向密封间隙对密封性能的影响Fig.7 Effect of radial sealing gap on sealing capacity

图8 密封间隙为0.7 mm时磁通量密度分布图Fig.8 Magnetic field distribution in 0.7 mm sealing gap

径向密封间隙高度和轴向密封间隙宽度值均为0.7 mm时，发散型阶梯式磁流体密封结构中磁通量密度分布情况如图8所示.根据发散型阶梯式磁流体密封理论(1)，计算出发散型阶梯式磁流体密封耐压能力为0.94 atm.说明通过有限元法计算出该阶梯式磁性液体密封结构的耐压能力小于磁路设计要求的耐压能力1.2 atm，这一现象是由漏磁造成的.从图9中可以明显看出，在永磁体与极靴结合处有明显的漏磁现象，其它地方并无明显漏磁，该问题可以通过选择非导磁壳体方法得以解决.

4 结论

1)采用磁路法初步设计了一种发散型阶梯式磁流体密封结构，得到了永磁体工作在最大磁能积位置处的最佳尺寸;

2)发散型阶梯式磁流体密封间隙内磁场有限元分析表明:发散型阶梯式磁流体密封耐压能力随着径向密封间隙的增大而减小;

3)极靴与永磁体结合处漏磁是导致用磁路法设计的发散型阶梯式磁流体密封结构耐压性能偏高的原因;通过选择非导磁壳体方法提高磁路设计的精度.

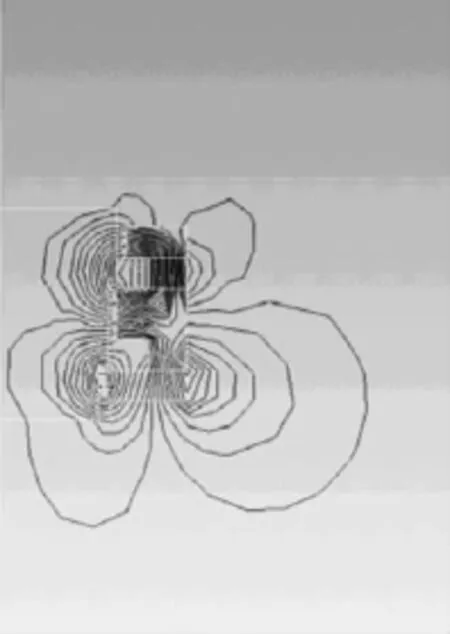
图9 磁力线分布Fig.9 Distribution of magnetic line of force

［1］ROSENSWEIG R E.Ferrohydrodynamics［M］.New York:Dover Publications，Inc，2002.

［2］YANG X L，ZHANG Z L，LI D C.Numerical and Experimental Study of Magnetic Fluid Seal with Large Sealing Gap and Multiple Magnetic Sources［J］.Science China-Technological Sciences，2013，56(11):2865-2869.

［3］WANG Z，LI D.Theoretical Analysis and Experimental Study on Loading Process among Stages of Magnetic Fluid Seal［J］. International Journal of Applied Electromagnetics and Mechanics，2015，48:101-110.

［4］LI Z，RAJ K.Effect of Vacuum Level on Evaporation Rate of Magnetic Fluids［J］.Journal of magnetism and magnetic materials，2004，289:43-46.

［5］OZAKI K，FUJIWARA T.An Experimental Study of High-speed Single Stage Magnetic Fluid Seals［J］.Journal of magnetism and magnetic materials，1987，65(2-3):382-384.

［6］ZOU J B，LI X H，LU Y P，et al.Numerical Analysis on the Action of Centrifuge Force in Magnetic Fluid Rotating Shaft Seals［J］. Journal of magnetism and magnetic materials，2002，252:321-323.

［7］束文强，谭光兴，刘梦，等.模糊控制在纯电动汽车永磁同步电机上的应用［J］.广西科技大学学报，2015，26(3):1-6.

［8］谢超艺，罗文广，张午昀，等.基于AD5435的永磁同步电机矢量控制系统仿真［J］.广西科技大学学报，2015，26(2):8-13.

［9］李德才，杨文明.大直径大间隙磁性液体静密封的实验研究［J］.兵工学报，2010，31(3):355-359.

［10］杨小龙，李德才，杨文明，等.大间隙磁流体密封的磁场有限元分析及实验验证［J］.北京交通大学学报，2013，37(1):181-184.

Magnetic field element finite analysis of diverging stepped magnetic fluid seals

YANG Xiao-long，LU Wen-li，SUN Kang-kang，CHEN Yan-hui
(School of Mechanical Engineering，Guangxi University of Science and Technology，Liuzhou 545006，China)

A new type of the stepped magnetic fluid seal is proposed based on the stepped labyrinth seal to improve universal magnetic fluid seal capacity.To obtain the maximum magnetic energy product，the magnetic circuit design was performed for diverging stepped magnetic fluid seal with two magnetic sources on the basis of stepped magnetic fluid seal theory.The magnetic field element finite method was adopted to calculate magnetic field distribution and stepped magnetic fluid seal capacity.The results are analyzed and discussed.It is demonstrated that the diverging stepped magnetic fluid seal capacity decrease with the increasing height of the radial sealing gap;magnetic field leakages at the connections of pole pieces and permanent magnets result in the sealing capacity of stepped magnetic fluid seal higher than universal magnetic fluid seal.

magnetic circuit;large gap;magnetic fluid;seal;numerical calculation

TH136

A

2095-7335(2016)02-0075-06

10.16375/j.cnki.cn45-1395/t.2016.02.013

(学科编辑:黎娅)

2015-12-17

广西自然科学基金项目(2015GXNSFAA139271);广西教育厅项目(KY2015ZD071)资助.

杨小龙，博士，讲师，研究方向:磁流体动力学研究，E-mail:yangxiaolong2004@126.com.