解二维Poisson方程离散化线性方程组的新型二次PEk方法

刘丽华

(广西科技大学理学院，广西柳州545006)

解二维Poisson方程离散化线性方程组的新型二次PEk方法

刘丽华

(广西科技大学理学院，广西柳州545006)

建立求解二维Poisson方程边值问题离散得到的大型块三对角线性代数方程组的新型二次PEk方法.验证了系数矩阵为M-矩阵的情形，证明了该问题利用新型二次PEk方法的可行性，最后用数值例子说明.

二维Poisson方程;离散化线性方程组;新型二次PEk方法;块三对角矩阵

0 引言

近年来，有许多学者研究二维Poisson问题的数值求解方法.文献［1］应用Chebyshev-Tau方法得出二维Poisson问题的线性代数方程组，再利用Chebychev Galerkin方法求解线性方程组的近似解;文献［2］则提出用多极理论来计算二维Poisson方程边值问题;文献［3-4］分别利用遗传改进算法和交替方向法求解二维Poisson问题.但二维Poisson方程带Dirichlet边界条件边值问题差分格式理论应用比较复杂，极少有文献研究差分格式相应的线性代数系统，文献［5］利用五阶WENO有限差分法实现了线性双曲守恒律方程的求解;文献［6］利用并行算法(PBOERA算法)对二维Poisson方程差分格式相应的代数系统进行求解，但它需要强大的并行计算机实验;文献［7］研究一般微机就能计算的方法，并研究Matlab在动力系统中的应用.张凯院等［8］给出了二次PEk方法，任水利等［9］给出了新型二次PEk方法，这些方法是求解块三对角线性代数方程组行之有效的方法，具有迭代收敛快及存储量小等优点.本文给出从二次Poisson问题的九点差分格式得到的块三对角矩阵［6］，由文献［9］给出新型二次PEk方法得出其数值解，并使用Matlab进行编程求解.

1 二维Poisson方程边值问题差分格式

考虑二维Poisson方程边值问题［6］:

式(1)中，0＜x＜a，0＜y＜b，u|x=0=φ1(y)，u|x=a=φ2(y)，u|y=0=φ3(x)，u|y=b=φ4(x).

式(1)的九点差分格式可写成如下块三对角线性方程组形式［5］:

2 新型二次PEk方法

九点差分格式块三对角线性方程组的系数矩阵为:

其中为k参数，相应的迭代格式(10)称为新型二次PEk方法.

3 二维Poisson问题新型二次PEk方法的可行性

定义1［10］若矩阵A=(aij)n×n满足aij≤0(i≠j;i，j=1，2，…，n)，且A-1≥0，则称A为M-矩阵.

定义2［10］若A∈Rn×n，若A=M-N，M-1N≥0且N≥0，则称A=M-N为A的正规分裂.

引理1［11］若A为M-矩阵，则由式(7)给出的分解式A=M-N中的矩阵M满足M-1≥0.

定理1由九点差分格式得出的二维poisson方程离散化的线性方程组系数矩阵为A为M-矩阵.

时，新型二次PEk方法收敛.

定理3由九点差分格式得出的二维Poisson方程离散化线性方程组可以利用新型二次PEk方法求解.

证明:由定理1可知A为M-矩阵.

因为:

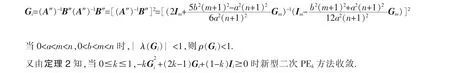
4 数值实验

下面通过试验说明用新型二次PEk方法求解二维Poisson方程边值问题的有效性.取a=1，b=2，m=3，根据n和k的取值不同得出算法的迭代次数和计算时间，如表1所示:

表1 迭代次数和计算时间Tab.1 The number of interations and computation time

由上述数值实验可知，用新型二次PEk方法计算二维Poisson方程边值问题收敛快，k的取值只要在［0，1］内，算法计算时间变化不大.本实验所有的算例均在AMD E2-3000M APU 1.80 GHz CPU，4.00GB RAM，Windows 7系统下用MATLAB 7.0计算.相对于文献［5］中需要4台以上的处理器并行计算的速度要慢，但是该方法在矩阵阶数100以内是比较快的，算法也行之有效，是新型二次PEk方法的应用扩展.

［1］王建瑜，宋菲.二维Poisson方程的谱方法求解［J］.科学技术与工程，2009(12):3425-3428.

［2］郑勤红，戴雯，解福瑶，等.用多极理论计算二维Poisson方程边值问题［J］.云南师范大学学报(自然科学版)，2001，21(2):42-46.

［3］彭武，何怡刚，方葛丰，等.二维泊松方程的遗传PSOR改进算法［J］.物理学报，2013，62(2):55-64.

［4］刘相国，谢如龙，郝江锋.二维泊松方程的交替方向迭代法［J］.大理学院学报(综合版)，2010，10(9):1-5.

［5］汤淑芳，林贤坤，覃柏英，等.五阶WENO有限差分法在线性双曲守恒方程中的应用［J］.广西科技大学学报，2015，26(1):90-95.

［6］张衡，张武.二维Poisson方程边值问题的块三对角可扩展并行算法［J］.微电子学与计算机，2008，25(10):117-120.

［7］蔡世东，蔡朝霞，张妮妮.MATLAB在动力方程求解中的应用［J］.广西工学院学报，2006，17(1):74-76.

［8］张凯院，王自然.解线性代数方程组的二次PE方法和二次PEk方法［J］.西北工业大学学报，2003，21(3):340-343.

［9］任水利，张凯院，叶正麟.解线性代数方程组的新型二次PEk方法［J］.高等学校计算数学学报，2006，28(2):176-184.

［10］周少玲，张凯院.系数矩阵为特殊M-矩阵的线性方程组的PEk解法［J］.兰州理工大学学报，2009，35(1):159-163.

［11］胡家赣.线性方程组的迭代解法［M］.北京:科学出版社，1999.

A new quadratic PEkmethod for solving linear algebraic equations derived from discretizing two-dimensional Poisson equation

LIU Li-hua
(College of Science，Guangxi University of Science and Technology，Liuzhou 545006，China)

In this paper，we propose the new quadraticPEkmethod for solving a system of large scale linear algebraic equations with block-tridiagonal matrix derived from discretizing two-dimensional Poisson equation.The condition that the coefficient matrix is M-matrix is verified，and the feasibility of the new method is proved，finally a numerical example is given to show that.

two-dimensional Poisson equation;discretizing linear algebraic equations;new quadraticPEkmethod; block-tridiagonal matrix

O151

A

2095-7335(2016)02-0100-04

10.16375/j.cnki.cn45-1395/t.2016.02.017

(学科编辑:张玉凤)

2015-10-22

广西高校科学技术研究项目(KY2015LX177，YB2014203);广西科技大学科学基金项目(校科自1419204)资助.

刘丽华，硕士，讲师，研究方向:数值与运筹优化方向，E-mail:lzhliga@163.com.