圆锥曲线中有关线段最值问题的解决方法

☉湖北省武汉中学　邹锦辉

圆锥曲线中有关线段最值问题的解决方法

☉湖北省武汉中学邹锦辉

在圆锥曲线中，经常遇到求圆锥曲线上的动点到某个点或者直线距离的最值问题，往往会考虑这个点就是圆锥曲线的特殊点，这很容易产生错误.在圆锥曲线中距离也可延续到面积和线段长度的组合问题等，这些问题都可以根据圆锥曲线的标准方程用适当的形式转化线段，将数学问题通过数形结合达到求解的目的，实际上就是问题的转化过程.

一、求圆锥曲线上的动点到定直线距离的最值问题的解决方法

一般来说，可以直接用点到直线的距离公式，再利用曲线方程的表示形式转化为一元二次函数利用其性质解决最值问题，也可以巧妙地利用判别式解决最值问题.其步骤如下：

第一步，设出与这条直线平行的圆锥曲线的切线y= kx+b.

第二步，切线方程y=kx+b与曲线方程联立，消元得到一个一元二次方程，由Δ=0，求出b的值，即可求出切线方程.

第三步，两平行线间的距离就是所求的最值.

例1已知点P在直线x+y+5=0上，点Q在抛物线y2= 2x上，则|PQ|的最小值等于_______.

解析：设与直线x+y+5=0平行且与抛物线y2=2x相切的直线方程是x+y+m=0，则由2m=0.

所以dmin=

例2求抛物线y=-x2上的点到直线4x+3y-8=0的距离的最小值.

解析：设与抛物线y=-x2相切且与直线4x+3y-8=0平行的直线方程为

二、利用圆锥曲线的定义进行转化的方法

解析几何的本质是用代数的方法解决几何问题，是数形结合的最好体现，所以在学习圆锥曲线时，数形结合思想必将起到重要的作用.此类问题众多，根据圆锥曲线的不同性质特点将线段转换成特殊位置的线段，比如，可以形成三角形三边，利用三角形三边不等式的性质解决问题.方法步骤可以为：

第一步，根据圆锥曲线的定义，把所求的最值转化为平面上两点之间的距离、点线之间的距离等.

第二步，利用两点间线段最短，或垂线段最短，或三角形的三边性质等找到取得最值的临界条件，进而求出最值.

例3已知A（3，2），F为抛物线y2=2x的焦点，M为抛物线上任一点，求|MF|+|MA|的最小值及取得最小值时M点的坐标.

解析：如图1所示，抛物线y2= 2x的准线方程为过M作 MQ垂直准线于Q 点.

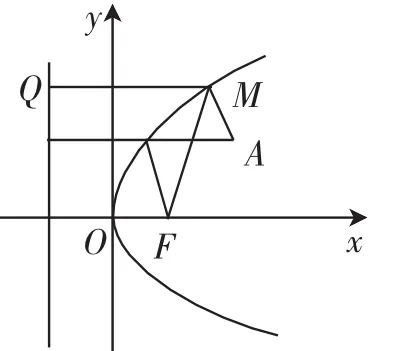
图1

由抛物线定义，得|MQ|=|MF|.

所以|MF|+|MA|=|MA|+|MQ|.

要使|MA|+|MQ|最小，则A，M，Q三点必共线，即AQ垂直于准线，AQ与抛物线的交点为M.

三、可以利用方程组联立转换成函数的方法

将圆锥曲线方程联立转化成函数利用函数的性质来解题.

第一步，把所求最值或者最值的目标表示为关于某个变量的函数.

第二步，通过研究这个函数求最值，是求各类最值最为普遍的方法.

例4若点P在抛物线y2=x上，点Q在圆（x-3）2+y2=1上，则|PQ|的最小值为_______.

所以dmin=

例5设P、Q分别是圆x2+（y-6）2=2和椭圆上的点，则两点间的最大距离是_______.

解析：设椭圆上的点为（x，y）.

因为圆x2+（y-6）2=2的圆心为（0，6），半径为所以椭圆上的点与圆心的距离为

四、利用基本不等式法消去参数得到结果

其基本步骤为：

第一步，将所求最值的量用变量表示出来.

第二步，用基本不等式求这个表达式的最值，并且使用基本不等式求出最值.

例6已知椭圆C1：和动圆C2：x2+y2=r2（r>0），直线l：y=kx+m与C1和C2分别有唯一的公共点A和B.

（Ⅰ）求r的取值范围；

（Ⅱ）求|AB|的最大值，并求此时圆C2的方程.

分析：（Ⅱ）利用（Ⅰ）中的方程求出A、B两点的横坐标，写出A、B两点间的距离，利用k、m、r之间的关系把两点间的距离转化为含有r的函数式，利用基本不等式求|AB|的最大值，并求出此时圆C2的方程.

由于直线l与C1有唯一的公共点A，故Δ1=64k2m2-16（1+4k2）·（m2-1）=0，从而m2=1+4k2①.

由于直线l与C2有唯一的公共点B，故Δ2=4k2m2-4（1+

由①、②得k2=

由k2≥0，得1≤r2＜4，所以r的取值范围是［1，2）.

（Ⅱ）设A（x1，y1），B（x2，y2），由（Ⅰ）的解答可知x1=

五、圆锥曲线中的最值和范围问题也可以利用参数法解决问题

其基本步骤为：

第一步，根据曲线方程的特点，用适当的参数表示曲线上点的坐标.

第二步，将目标函数表示成关于参数的函数.

第三步，把所求的最值归结为求解关于这个参数的函数的最值的方法.

圆锥曲线中线段长度和距离最值问题在高考中一直是个重点，同时也是一个难点，其特点是难度较大，并且运算量大，较难得分.如何处理好这个问题，通过本节介绍的方法归类尽量简化计算达到做题的目的.F