例说抢拿分数的五种技巧

☉湖北省安陆市第一高级中学　伍海军

例说抢拿分数的五种技巧

☉湖北省安陆市第一高级中学伍海军

又是一年高考时，笔者就如何在考场上抢拿分数，寄语高三学子.

据统计，考生解答每个问题平均只有3分钟时间，因此建议第Ⅰ卷用时最多不要超过40分钟，会做的题一定要首先完成.试卷上的参考公式，80%是有用的，注意括号里的文字，往往是解题的关键；一些具体的计算细节可以不写，但是关键步骤必须有，要根据分值思考要点，如2012年高考湖北卷理科立体几何题总分12分，评分时就有12个给分点，一个点1分.

函数、方程或不等式的题目，首先考虑定义域；圆锥曲线优先选择定义法完成；直线与圆锥曲线相交问题，若与弦的中点有关选择设而不求点差法，与弦的中点无关的则选择韦达定理公式法；使用韦达定理必须先考虑是否为二次及根的判别式；立体几何第一问如果是为建系服务的，建议用传统方法，如果不是，可以直接从第一问开始建系.

在答题框解答第一问后，如第二问不会做但对第三问有感觉，这时不少学生习惯在第二问留下空白位置，但评卷时一些视力不太好的老师很有可能以为下面没有文字，这样第三问就看不到了；书写要能看清，比如a和9，n和12，5和3，4和x，负号和分数线离得太近没法辨认等；对于解题方法，虽未做过多的限制，但因为高考评卷时间紧，任务重，天气热，一些独创的方法极有可能被误判.

解答题中答案是最重要的，只有答案错误时阅卷老师才不得不看你的解题过程，再去找得分点.很多试卷是经不起细看的，笔误，步骤不完整，可能都会扣分，另外如果没有新思路，不要把写的删了；考后和同学对答案是大忌只会造成更加的慌乱，尽量避免与同学同行.下面举几例说明如何抢拿分数.

一、书写定理拿公式分

例1（2013年高考新课标卷Ⅰ理）如图1，在△ABC中，∠ABC=90BC=1，P为△ABC内一点，∠BPC=90°.

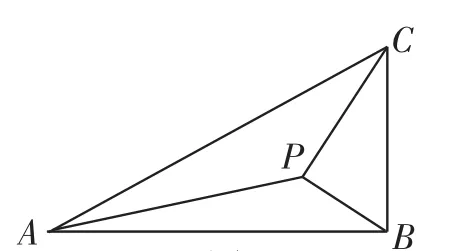
图1

（Ⅱ）若∠APB=150°，求tan∠PBA.

此题是解三角形，解三角形题的主要方法是利用正余弦定理.在（Ⅰ）中，易得∠PBA=30°，于是在△PBA中，已知两边及夹角求PA该用余弦定理，为防止计算错误，可先将余弦定理写出：PA2=PB2+AB2-2PB·ABcos∠PBA，这样即使后面计算错误还是可以得分的.同理，（Ⅱ）中可先写出正弦定理得公式分.

二、跳过推理拿结果分

例2（2015年高考新课标卷Ⅰ理）Sn为数列｛an｝的前n项和，已知

该题对于基础较差的学生也许有难度，但可以依据递推公式算出前几项3，5，7，…，发现规律，猜测出通项公式为an=2n+1，得结果分，再利用此结果做（Ⅱ），则（Ⅱ）仍可得满分.

三、越过障碍拿后续分

例3（2015年高考湖北卷理21）题略.

主要难点在（Ⅰ），很多学生不能求出轨迹方程导致（Ⅱ）无从下手，其实（Ⅱ）比较常规，部分学生比较灵活，选取几个特殊位置大胆猜测轨迹为椭圆，并由此写出椭圆方程，按此结论做下去，第二问仍可得满分.

四、虚补条件拿逻辑分

例4（2015年高考新课标卷Ⅰ理18）如图2，四边形ABCD为菱形，∠ABC=120°，E、F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE= 2DF，AE⊥EC.

（Ⅰ）证明：平面AEC⊥平面AFC；

（Ⅱ）略.

连接BD交AC于点G，易得EG⊥AG，要证平面AEC⊥平面AFC，则还需证EG垂直平面AFC内某一直线，如果实在无法证出，可根据需要自行补充EG⊥FG再继续证明，尽管丢失此处得分点，但不会影响后面得分.

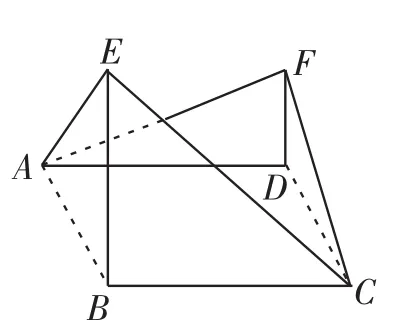
图2

五、将错就错拿补偿分

例5（2014年高考新课标卷Ⅰ理20）已知点A（0， -2），椭圆E（a＞b＞0）的离心率为，F是椭圆E的右焦点，直线AF的斜率为，O为坐标原点.

（Ⅰ）求E的方程；

（Ⅱ）设过点A的动直线l与E相交于P、Q两点，当△OPQ的面积最大时，求l的方程.

依据高考阅分原则，如果学生在有一处错误的前提下一直计算下去而并没再犯错，则后面的分数减半，最高不能超过（Ⅱ）中分值一半.如此题有学生在（Ⅰ）中将方程写成依此错误方程计算（Ⅱ），设P（x1， y1），Q（x2，y2），直线l的方程y=kx-2，联立，化简得（3+4k2）x2-16kx+4=0，当Δ>0时，解得，得x1+x2=等几个关键式子均没出错，仍可按高考阅卷原则减半给分.F