基于小波包能量谱的古木结构损伤识别

杨帆，王鑫

（天水师范学院 土木工程学院，甘肃 天水 741001）

基于小波包能量谱的古木结构损伤识别

杨帆，王鑫

（天水师范学院 土木工程学院，甘肃 天水 741001）

通过对古木结构损伤进行有限元分析，提出了随机激励作用下古木结构的小波包能量变化率指标，表明该指标对于古木结构的损伤比较敏感，可以准确地判定古木结构损伤出现的位置，损伤程度越大，此指标越大。随后又提出了古木结构损伤程度的判定方法，并验证了其适用性，为研究环境激励下古木结构的损伤识别奠定了理论基础。

古木结构；有限元；小波包能量谱；损伤识别；小波包能量变化率

0　引言

古木结构在环境的侵蚀下、材料出现的老化和荷载的长期作用及其疲劳效应下，难免会出现结构系统的损伤，因此需要在第一时间结构健康监测系统及时发现结构出现的损伤并进行预警。传统的模态参数不能准确识别出结构的损伤，大多数是通过振动的损伤评估方法由瞬态信号的傅立叶变换得出模态参数[1,2]，而傅立叶变换最大缺陷是对高频模态分析不足，从时域到频域的变换过程中时域的信息会丢失，不可能准确评价结构的损伤特性。小波分析有放大、缩小和平移等功能，通过检查不同放大倍数下的变化来研究信号的变化特征，有优良的时-频域特性，但缺点是高频段分辨率差。小波包变换是小波变换的扩充，它将频带多层次划分，对多分辨分析没有细分的高频部分进一步来分解，通过分析信号的特征，自适应地选择相应频带，提高了时-频分辨率，因此小波包应用更加广泛。

丁幼亮等[3]提出了小波包能量谱的大跨桥梁结构损伤预警指标，刘涛等[4]在小波包能量谱的损伤预警基础上建立了大跨悬索桥损伤预警方法，Hong等[5]对模态振型进行连续的小波变换，利用Lipschitz指数判定损伤出现的位置，李功宇等[6]采用曲率模态分析方法准确识别悬臂梁损伤出现位置，并进一步判断悬臂梁的损伤程度，韩建刚等[7]提出小波包变换的能量变化率指标对梁体进行损伤定位研究。

本文提出小波包能量变化率指标对古木结构进行损伤识别，表明小波包能量变化率指标对于损伤识别较敏感，能够准确地判定损伤的具体位置，随后研究了小波包能量变化率指标应用于古木结构损伤识别的有效性。

1　小波包分析

小波包由小波函数线性组合而成，其中i、j、k分别为小波包函数的频率参数、尺度参数和平移参数：

小波函数ψi由右式求解:

对于任意信号的第j阶和第j+1阶小波包分解的递推关系是:

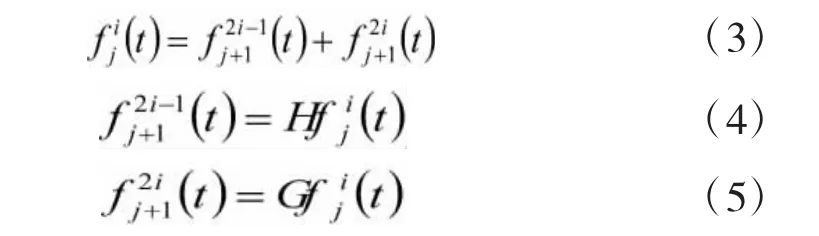
其中，H和G分别表示对应于h(k)和g(k)的滤波算子，经过j水平的小波包分解后，初始信号f(t)为:

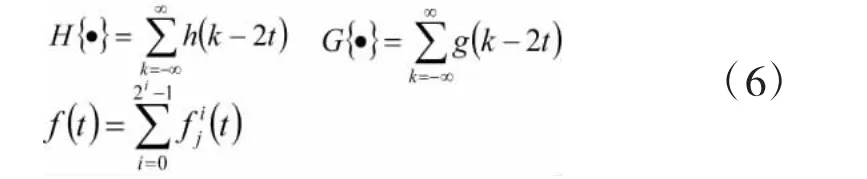
小波包系数为:

2　损伤识别参数的选择

2.1选择合理的小波函数

从消失矩和支撑长度来看，选用Daubechies损伤定位的小波函数。N越大，Daubechies的消失矩越高，时域的分辨率越好；但Daubechies支撑长度越宽，小波的时域局域性越差。因此需合理确定Daubechies小波阶次N。

对结构动力响应进行第i层小波包分解，fij表示第i层分解节点(i，j)上的结构响应，每个频带的结构响应fij能量为[8]:

结构动力响应在第i分解层的小波包能量谱向量Ei为:

小波包能量谱各频带能量系数Eij时频集中程度通过代价函数M{Eij}来反映，采用lp范数熵作为代价函数，在同一小波包分解层上，计算不同小波函数的代价函数值，确定较适合的Daubechies小波阶次N。通常不同的阶次计算小波函数的代价函数值越小越好，lp范数熵(1≤p≤2)为[8]：

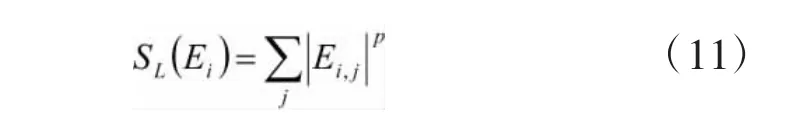
2.2选择合理的小波包分解层数

实际工程中把结构动力响应进行小波包分解，计算每一分解层次上的小波包能量谱的代价函数，由代价函数和计算时间综合考虑来确定适当的小波包分解层次，通常小波包能量谱代价函数值越小，计算机计算消耗时间越少，小波包分解层次将越好。类似选择小波函数阶次，采用lp范数熵代价函数来确定合适的小波包分解层数，lp范数熵(1≤p≤2)为[8]：

2.3小波包能量变化率指标

定义j水平下的信号能量Efj为:

由正交性条件得到:

任伟新等[9,10]定义能量变化率指标，j分解水平下信号小波包能量变化率指标Δ(Efj)为：

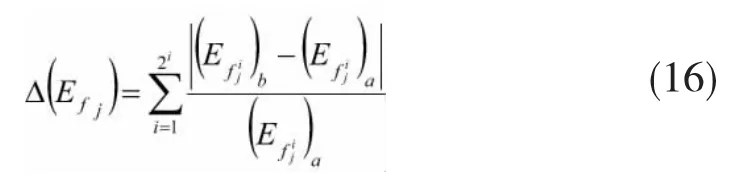
本文进一步提出对损伤定位更敏感的指标——新的能量变化率指标NΔ(Efj)：

3　算例

3.1古木结构的损伤模拟

本文采用有限元软件对环境激励下一榀古木框架结构进行损伤模拟，选取木梁长4 m，木柱高6m，梁截面尺寸为300 mm×700 mm，柱截面直径500 mm。梁柱榫卯连接采用Combinl4单元。用beam188梁单元模拟木柱、木梁，榫卯连接的弯曲刚度为[11]：1×1010kN·m/rad，木材的弹性模量取1×1010N/m2，泊松比为0.25，密度为410 kg/m3，采用Rayleigh定义的粘性比例阻尼。计算中未考虑屋面质量，墙体不承重，不予考虑。柱子搁置在凹槽柱础上，不能完全限制柱子转动，柱与基础连接简化成固定铰支座的力学模型符合实际情况[12,13]，建立古木结构的有限元模型如图1所示。

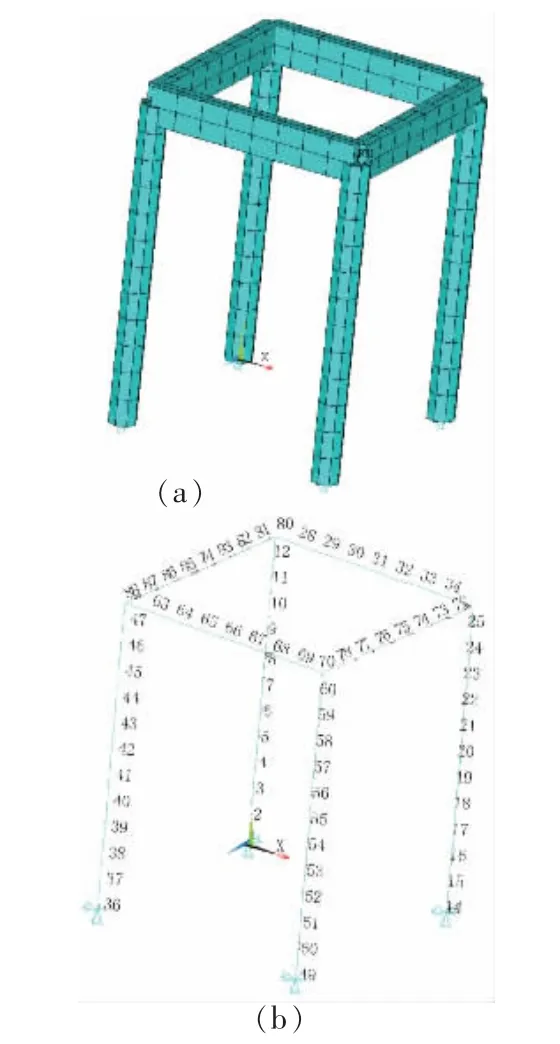
图1　古木结构的有限元模型(a)和节点详图(b)

在模型支座1施加水平方向的激励荷载选用交通荷载[14]，激励荷载的时程曲线及频谱如图2所示，获得结构的加速度荷载时程，采用Matlab程序计算了小波包能量谱。

图2　激励荷载的时程曲线图（a）及频谱曲线图（b）

表1　列出了古木结构的损伤工况，损伤程度通过折减损伤单元的弹性模量来实现，其中10%、18%、20%分别指损伤单元的弹性模量减少10%、18%、20%[8]。

对损伤工况1、2进行分析，得出完好结构和损伤工况1、2梁跨中第31节点的竖向加速度时程曲线如图3所示。从图3看出各损伤工况的信号有一定差别，但很难判断出古木结构的损伤情况。因此下面从小波函数的选择、小波分解层次的选择、损伤定位参数的选择讨论古木结构的损伤识别过程。

3.2确定计算参数

3.2.1小波函数的选择

因梁跨中挠度较大，以完好结构梁跨中第31节点的竖向加速度响应为例，采用不同阶次Daubechies小波对其进行小波包分解，分解层次为4，计算范数熵代价函数值如表2所列。从表2看出小波阶次为20时，范数熵为5592.46，其值相对其他小波阶次最小，因此损伤识别的小波函数选取Daubechies20。

图3　梁跨中第31节点加速度响应图示

表2　分解层次为4时不同db小波的代价函数值一览表

3.2.2小波包分解层数的选择

采用Daubechies20小波对梁跨中第31节点完好状态下的竖向加速度响应进行小波包分解，分解层次分别取1～8，计算lp范数熵的代价函数值如表3所列。从表3看出分解层次为4时，代价函数值为5592.46，相应计算时间为0.109 s，代价函数和计算时间均相对较小，因此损伤识别的小波包分解层次取4。

表3　Daubechies 20不同分解层次的代价函数值和计算时间一览表

3.3损伤识别的判定

本文选择db20对梁上各节点完好结构和损伤工况1、2的竖向加速度响应信号进行小波包分解，分解层次取4。运用公式（16）求出各节点的能量变化率指标，再将其值与梁上各节点编号绘制如图4所示。

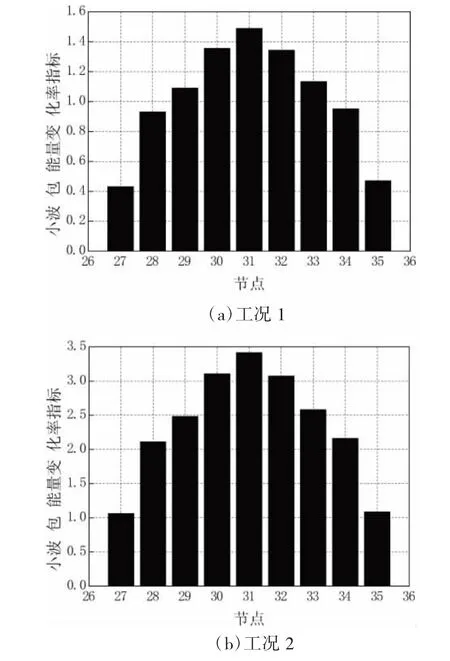
图4　小波包能量变化率指标柱状图(一)

从图4（a）、(b)看到，梁跨中节点31小波包能量变化率指标数值最大，与它相邻的节点30、32值次之，离节点31越远的节点值越小，到节点27、35值最小，可以判定在节点30、31、32之间存在损伤，正好是梁的损伤单元52、53所在位置，可判定在此处发生了损伤，此指标可准确地判定梁的损伤位置。随着损伤程度增大，小波包能量变化率指标的值在增大，因此可以定量和定性地判断古木结构梁的损伤情况。

同样对上述梁各节点的竖向加速度响应信号进行小波包分解，小波函数和分解层次与上述相同，能量变化率指标采用公式(17)计算，得到各损伤工况下梁上各节点的能量变化率指标如图5所示。

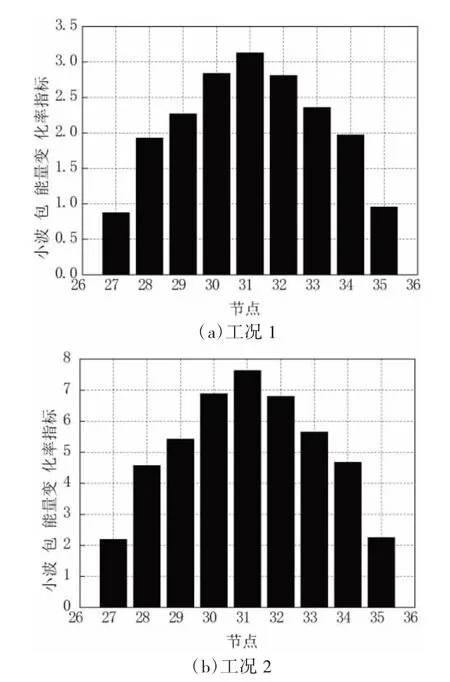
图5　小波包能量变化率指标柱状图（二）

从图5（a）、(b)同样看出，节点31能量变化率指标最大，与它相邻的节点30、32的值次之，离节点31越远的值越小，到节点27、35值最小，可判定在节点30、31、32间存在损伤，与损伤工况1、2的损伤单元52、53所在位置吻合，可判定在此处发生损伤，此指标可准确地判定梁的损伤位置。工况2的能量变化率指标明显比工况1大，与工况2的损伤程度大于工况1相符。随着损伤程度增大，能量变化率指标增大，因此可以定量和定性地判断古木结构梁的损伤情况。比较图4、图5可看出，相同的损伤工况、选用相同的小波函数和分解层次，采用式（17）能量变化率指标明显大于式（16）能量变化率指标，说明本文提出的能量变化率指标能更加敏感地表征古木结构梁的损伤位置，而且损伤程度越大，小波包能量变化率指标越大。

3.4判定损伤程度

由图4、图5可看出，损伤指标的图形形状基本相似，数值大小有差异。设想若能找到损伤程度和损伤指标间的函数关系，画出其关系曲线，知道了损伤指标，就可以判断损伤程度了。

假设古木结构梁跨中出现损伤，对梁跨中损伤程度10%、15%、20%、25%、30%、35%、40%进行数值模拟，得到相应的竖向加速度信号，由式（17）计算梁跨中的损伤指标——小波包能量变化率指标，采用matlab数值拟合找到节点31损伤程度与损伤指标的函数关系，各损伤工况节点31的损伤识别指标如表4所列，绘出其关系曲线如图6所示。

表4　损伤识别指标一览表

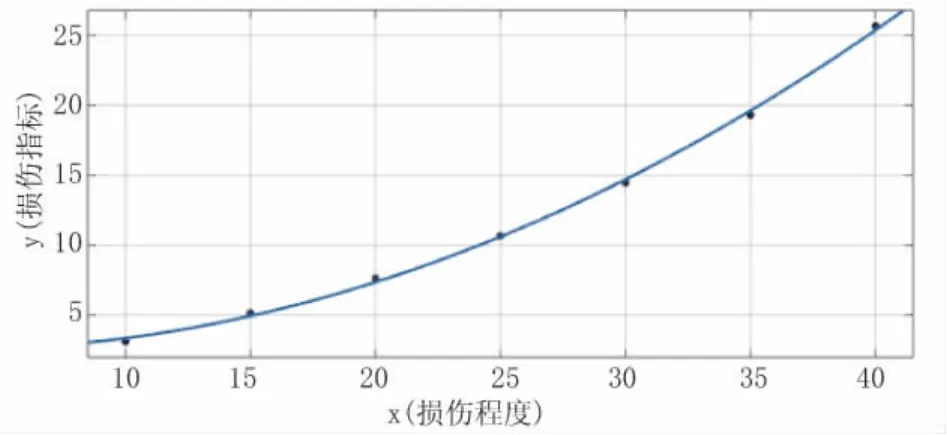
图6　损伤程度与损伤指标的关系曲线图

由图6得到损伤指标和损伤程度的函数关系式为：y=0.01668x2-0.1002x+2.703，对某损伤程度的结构施加一定的激励荷载，得到相应的加速度时程曲线，进行小波包分解，用式（17）求出损伤指标，就能在图6找到相应的损伤程度。

有效性的验证：假设梁跨中损伤程度为18%，对损伤工况3进行数值模拟，得到梁上各节点的竖向加速度时程曲线，进行小波包分解，绘制损伤指标如图7所示，节点31的损伤指标值y=6.590，由图6曲线可逆推出x=18.56%，误差为3.1%，因此该损伤指标与损伤程度的关系式能对古木结构的损伤程度进行较准确的识别。

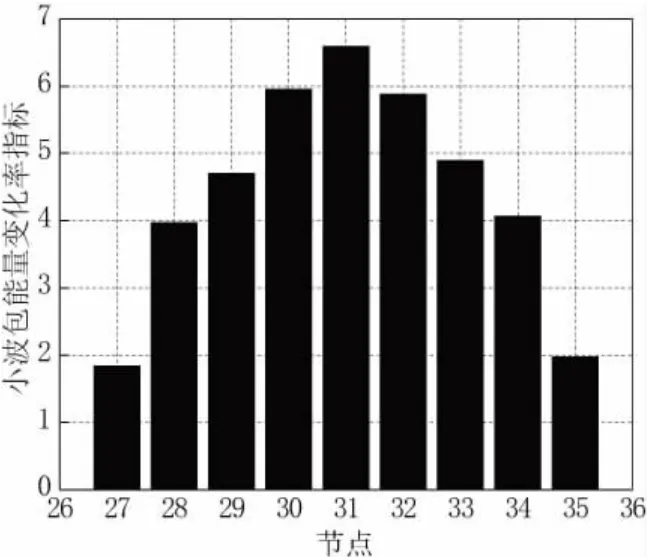
图7　工况3小波包能量变化率指标柱状图

4　结　语

（1）本文提出了小波包能量变化率指标，对随机荷载作用下的古木结构梁上各节点的加速度响应信号进行小波包分解，然后计算此指标，进行结构的损伤定位。

（2）小波包的能量变化率指标对于古木结构梁的损伤较敏感，可准确地判定古木结构梁的损伤位置。本文提出的能量变化率指标更能表征古木结构梁的损伤位置，损伤程度越大，小波包能量变化率指标越大。

（3）在损伤位置判定的情况下，又提出损伤程度的判定方法并验证了其有效性，为研究环境激励下古木结构的损伤识别奠定了理论基础。

[1]FarrarCR,JaureguiDA.Comparativestudyofdamage identification algorithms applied to a bridge:I.Experiment[J]. Smart Mater.Struct,1998（7）:704-719.

[2]FarrarCR,JaureguiDA.Comparativestudyofdamage identification algorithms applied to a bridge:II.Numerical Study [J].Smart Mater.Struct.,1998（7）:720-731.

[3]丁幼亮,李爱群,缪长青,等.基于小波包能量谱的大跨桥梁结构损伤预警指标[J].中国 公路 学报,2006,19(5):34-40.

[4]刘涛,李爱群,丁幼亮,等.大跨悬索桥损伤预警方法[J].特种结构，2005，22(3):83-85.

[5]Hong JC,Kim YY,Lee Hc.et.all.Damage detection using the Lipschitz exponent estimatedby the wavelet transform:application to Vibration modes of a beam[J].Int.J.Solids,stnlct.,2002（39）: 1803-1816.

[6]李功宇,郑华文.损伤结构的曲率模态分析[J].振动、测试与诊断,2002,22(2):136-141.

[7]Han JG,Sun ZS,Ren WX.Wavelet based damage identification of beams[A].In:Proceedings of the eighth international symposium on structural engineering for young experts[c].Beijing:sp,2004：356-363.

[8]李爱群,丁幼亮.工程结构损伤预警理论及其应用[M].北京:科学出版社,2007.

[9]Jian-Gang Han,Wei-Xin Ren,Zeng-Shou Sun.Wavelet packet based damage identification of beam structures[J].International Journal of Solids and Structures,2005（42）：6610-6627.

[10]韩建刚,任伟新,孙增寿.基于小波包变换的梁体损伤识别[J].振动、测试与诊断,2006,26(1):5-10.

[11]孟昭博.西安钟楼的交通振动响应分析及评估[D].西安:西安建筑科技大学，2009.

[12]孟昭博,袁俊,吴敏哲,等.古建筑高台基对地震反应的影响[J].西安建筑科技大学学报,2008，40(6):835-840.

[13]赵均海,俞茂宏,高大峰,等.中国古代木结构的弹塑性有限元分析[J].西安建筑科技大学学报,1999,31(2):131-133.

[14]韩广森.城市轨道交通微幅振动对古建筑的影响[D].西安:西安建筑科技大学,2011.

TU312

A

1009-7716（2016）03-0177-05

10.16799/j.cnki.csdqyfh.2016.03.051

2015-11-30

杨帆（1969-），男，甘肃庆阳人，讲师，院长，从事土木工程方面的教学与研究工作。