斜拉拱桥面内弹性稳定性研究

2016-11-24汪剑陆伟

城市道桥与防洪 2016年3期

关键词：固支斜拉拱桥

汪剑,陆伟

（武汉市政工程设计研究院有限责任公司，湖北武汉 430015）

斜拉拱桥面内弹性稳定性研究

汪剑,陆伟

（武汉市政工程设计研究院有限责任公司，湖北武汉 430015）

斜拉拱桥是一种新型的拱桥结构形式。本文对斜拉拱桥与普通拱桥平面模型的弹性稳定性进行了对比分析，计算分析了斜拉拱在不同矢跨比、边界条件、荷载工况下的面内弹性稳定性，并讨论了斜拉索张拉参数（在拱上张拉位置、斜拉索倾角）对斜拉拱桥平面内弹性稳定性的影响。

斜拉拱桥；稳定性；ANSYS

1　概述

索-拱组合体系在大跨度建筑结构中已得到广泛应用，其基本原理是通过在拱内张拉索来改善拱的受力性能。对于建筑上索-拱结构的面内稳定性，在国内已有较为成熟的研究[1-3]，而斜拉拱桥是一种不同于建筑索-拱、将预应力索张拉于拱外部的杂交拱式体系，国内已建湖南湘江四桥是国内唯一一座斜拉拱桥，目前对这种索-拱体系稳定性的研究较少[4-5]。本文通过斜拉拱桥平面模型和普通拱桥平面模型的对比计算，分析了不同矢跨比、边界条件、荷载工况下斜拉拱面内弹性稳定性，并讨论了斜拉索参数对斜拉拱面内稳定性的影响。

2　斜拉拱桥平面内的弹性稳定性分析

为了符合拱桥中受力实际情况，本文在平面计算模型中将拱、吊杆、桥面系作为一个整体进行考虑，荷载作用在桥面系上，通过吊杆传力到拱，这样能更综合全面地考虑影响拱面内失稳的各因素。采用ANSYS软件进行数值计算，pipe16单元模拟拱肋，link10单元模拟斜拉索和吊杆，beam188单元模拟桥面系。

【数值算例】对图1、图2所示的普通拱桥平面模型、斜拉拱桥平面模型进行特征值屈曲对比计算。对比计算主要是为了分析影响拱面内稳定性的因素，因此做了如下约定：

（1）两种平面模型的拱轴方程、拱肋的截面几何特性、施加荷载、边界条件相同。

图1　普通拱桥平面模型

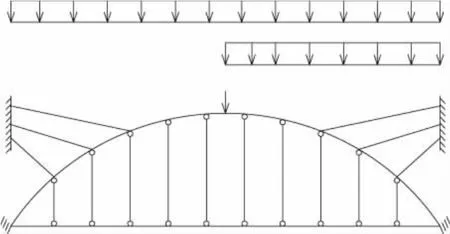
图2　斜拉拱桥平面模型

（2）不考虑自重荷载。

（3）斜拉拱模型中，假设塔的刚度无穷大，拉索远离拱的一端可简化为固端约束。

两种平面模型的基本参数与荷载如下：拱肋为抛物线，以左拱脚为坐标原点，其抛物线方程为，拱跨度为l=80m，矢高f=8～40 m，拱肋截面简化为方形，横截面积为0.64 m2，平面内抗弯惯性矩0.034 13 m4，弹性模量为2.06×1011Pa；斜拉索弹性模量为1.95×1011Pa，横截面积为0.002 m2；吊杆弹性模量为2×1011Pa，横截面积为0.002 m2。

三种荷载工况分别为满跨竖直均布荷载10 kN/m、半跨竖直均布荷载10 kN/m和跨中集中荷载400 kN，荷载作用在桥面系上，计算结果中的屈曲系数乘以所加荷载，即为结构弹性失稳的临界荷载。

计算为线弹性屈曲，只考虑平面内失稳。

三种荷载工况下，普通拱与斜拉拱两种平面模型的弹性屈曲系数随矢跨比变化规律的计算结果如图3～图6所示。

图3　集中荷载弹性屈曲系数

图4　半跨均布荷载弹性屈曲系数

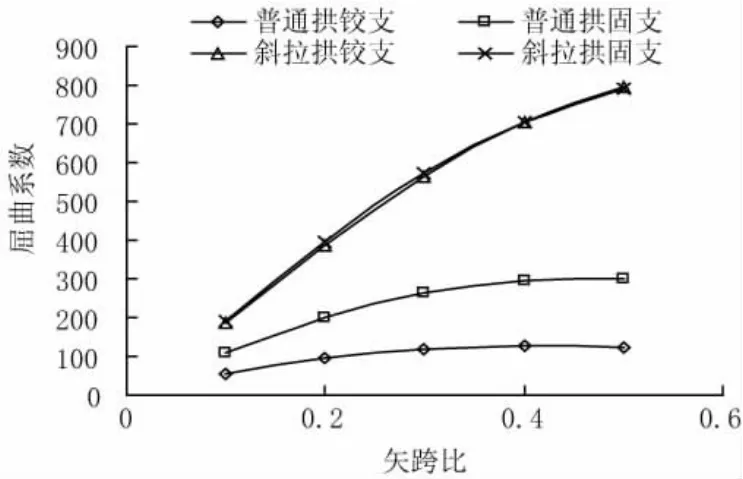
图5　满跨均布荷载弹性屈曲系数

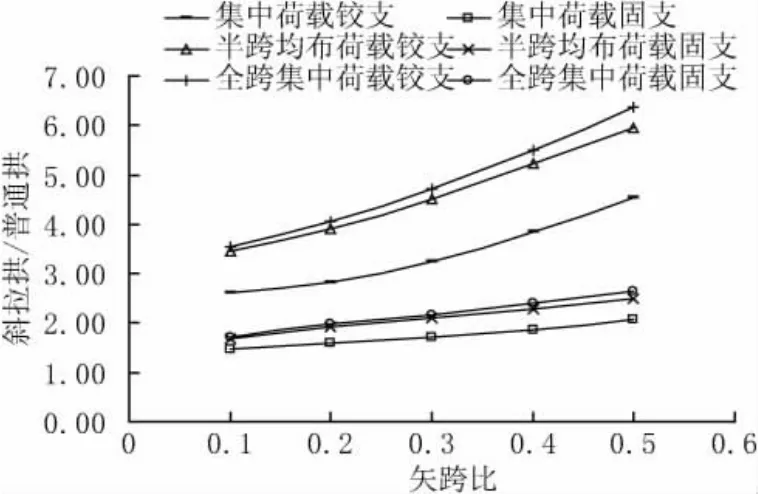
图6　斜拉拱/普通拱弹性屈曲系数增加倍数

（1）从图3～图5可以看出，斜拉拱在不同荷载工况下，弹性屈曲系数对边界条件不敏感，铰支、固支条件下弹性屈曲系数接近。这是由于斜拉索的存在，索、拱、吊杆、桥面系组成自平衡体系，导致边界条件对弹性屈曲的影响降低。

（2）从图3～图5可知，斜拉拱在不同荷载工况、边界条件下，在计算矢跨比范围内，随着矢跨比增加，弹性屈曲系数逐渐平稳提高，未出现极值点。

（3）从图3～图6可知，相对于普通拱，铰支边界条件时，不同荷载工况下斜拉拱弹性屈曲系数提高2.60～6.36倍不等，且随着矢跨比增加，提高倍数平稳增加。而对于固支边界条件，斜拉拱弹性屈曲系数提高1.47～2.63倍不等，且随着矢跨比增加，提高倍数缓慢增加。

3　斜拉拱的拉索参数对面内弹性稳定性的影响分析

对斜拉拱不同拉索张拉参数对弹性稳定性的影响进行计算分析，主要考虑斜拉索在拱上的张拉位置、斜拉索的倾角因素对斜拉拱面内弹性稳定性的影响。

3.1斜拉索在拱上位置的影响

在拱上布置单根斜拉索，分别布置在拱的L/10、2L/10、…、9L/10、L处（L为拱跨度的一半）。为了摒除长度与倾角变化造成的影响，索在任意点张拉时长度均为20 m，倾角均为20°，不同矢跨比、边界条件、荷载工况弹性稳定计算结果如图7～图12所示。

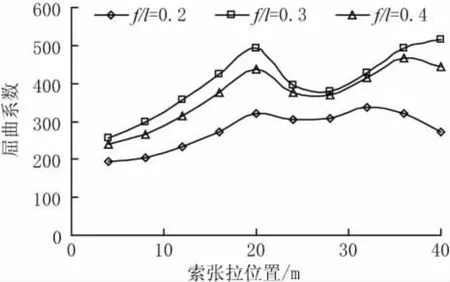
图7　集中荷载、固支边界屈曲系数

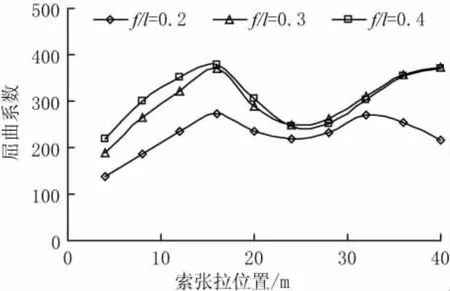
图8　集中荷载、铰支边界屈曲系数

图9　半跨均布荷载、固支边界屈曲系数

图10　半跨均布荷载、铰支边界屈曲系数

图11　全跨均布荷载、固支边界屈曲系数

图12　全跨均布荷载、铰支边界屈曲系数

（1）从图7、图8、图11和图12可以看出，在跨中集中荷载和全跨均布荷载作用下，边界条件为固支，矢跨比0.2时，斜拉索张拉于四分点和距拱脚32m时，斜拉拱面内弹性屈曲系数有极大值，矢跨比增加时，第二个弹性屈曲系数极大值的张拉位置变为拱顶。对于铰支边界条件，相比于固支边界，屈曲系数第一个极大值点的张拉位置更靠近拱脚，位于距拱脚水平距离16 m处。

（2）从图9和图10可以看出，在半跨均布荷载作用下，边界条件为固支、矢跨比为0.2和0.3、斜拉索张拉在四分点时，斜拉拱面内弹性屈曲系数出现最大值，索张拉位置向拱顶或拱脚靠拢时，屈曲系数减小。矢跨比增加到0.4时，使斜拉拱面内弹性屈曲系数出现最大值的斜拉索张拉位置向拱脚靠近，位于距拱脚水平距离16 m处。边界条件为铰支时，相比于固支边界，使屈曲系数达到最大值的斜拉索张拉位置更靠近拱脚。

3.2斜拉索倾角的影响

对单根斜拉索布置于拱上不同位置，拉索长度取25 m，拉索按倾角0°、10°、20°、…、80°、90°布置，仅考虑半跨均布荷载作用的情况，计算结果如图13～图18所示。

图13　矢跨比0.2、固支边界屈曲系数

图14　矢跨比0.2、铰支边界屈曲系数

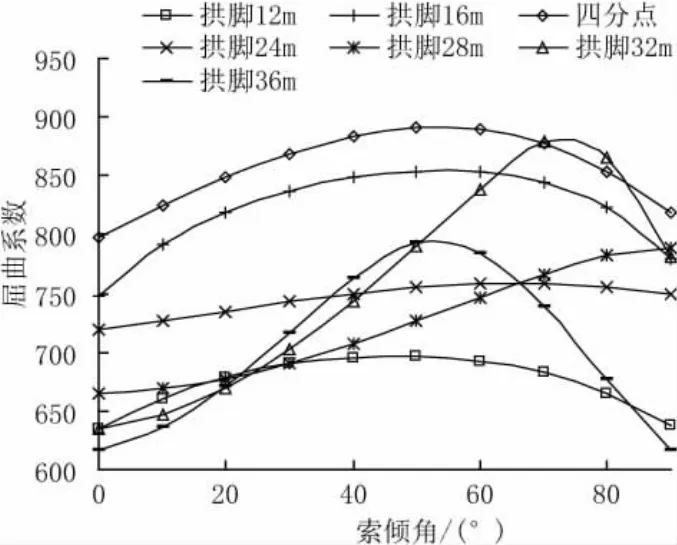
图15　矢跨比0.3、固支边界屈曲系数

图16　矢跨比0.3、铰支边界屈曲系数

图17　矢跨比0.4、固支边界屈曲系数

图18　矢跨比0.4、铰支边界屈曲系数

（1）从图13～图18可知，不同矢跨比、边界条件和斜拉索张拉在拱上不同位置，弹性屈曲系数随拉索倾角的变化规律均不同。

（2）从图13、图15、图17可以看出，对于不同矢跨比，在固支边界条件下，当斜拉索张拉位置位于距拱脚水平距离28 m到拱顶范围内，屈曲系数随索倾角的变化呈曲率较大的抛物线规律，抛物线顶点处的斜拉索倾角从90°降至70°、50°，矢跨比越大，抛物线曲率越大，即不同索倾角的屈曲系数差别越大。

（3）从图14、图16、图18可以看出，相对于固支边界，铰支边界条件下，索张拉于距拱脚水平距离28m至拱顶范围内时，随着倾角的变化、屈曲系数变化范围较小，随着矢跨比增加，索张拉靠近拱顶时，最优倾角逐渐增加，从40°增加到70°。

（4）斜拉索张拉于拱脚到距拱脚水平距离24 m范围内，最优倾角为60°～70°，且在包括最优倾角约40°角度范围内，屈曲系数差别较小，在5%以内。

4　结论

本文通过建立斜拉拱平面模型，对斜拉拱面内弹性稳定性进行了计算分析，得出了如下结论：

（1）相对于普通拱桥平面模型，斜拉索能极大地提高拱面内弹性稳定性，特别是对铰支边界条件，且由于斜拉索减小了拱脚推力，斜拉拱在铰支、固支边界条件下弹性稳定性差别缩小。

（2）对面内弹性稳定性而言，在不同荷载工况、矢跨比、边界条件下，斜拉索在拱上的最佳张拉位置均不相同，总的来说，在集中荷载作用下，固支边界、矢跨比为0.2时，索最优张拉位置为四分点和约3L/8处，矢跨比增加，索最优张拉位置为四分点和拱顶。半跨均布荷载作用下，固支边界、矢跨比为0.2时，索最优张拉位置为四分点，矢跨比增加，最优张拉位置向拱脚靠近。全跨均布荷载作用下索最优张拉位置与半跨荷载相同，但随着拉索布置从最优位置变化至拱顶，斜拉拱面内屈曲系数先减小再增加。对于不同荷载工况下的铰支边界，相对于固支边界，索的最优张拉位置向拱脚靠近。

（3）对面内弹性稳定性而言，当索张拉于拱上的不同位置时，索最优倾角均不相同，总的来说，在拱脚到约四分点范围内，最优倾角为60°～70°，且在包括最优倾角约40°的角度范围内，屈曲系数差别较小，在5%以内。索张拉位置位于约四分点至拱顶范围内时，越靠近拱顶，最优倾角越小，且在最优倾角两边角度范围内，弹性屈曲系数变化较大。

[1]王江.索-拱杂交结构线性稳定性初探[J].华北航天工业学院学报，2004，14(4)：19-20,24.

[2]剧锦三，郭彦林.索-拱结构的平面内稳定性研究[J].建筑结构学报，2001，22（2）：84-87.

[3]胡淑辉.索-拱结构的稳定性能研究[D].北京：清华大学，2005.

[4]赵跃宇，刘伟长，杨相展.大跨径斜拉钢管混凝土拱桥空间稳定性分析[J].公路，2006(8)：68-71.

[5]陆伟.大跨度组合式斜拉-拱桥的稳定性研究[D].武汉：武汉大学，2008.

北京“大外环”已通车367 km张家口承德间可直达

作为北京“大外环”重要的组成部分，全长367 km的张家口—承德高速公路建成通车。这将极大缓解北京过境车辆的压力，为全长940 km北京“大外环”的早日贯通奠定了重要基础。

张承高速公路按双向4车道标准建设，分张家口和承德两段。其中张家口段全长164 km，分两期建设。承德段全长203 km。张承高速公路的建成通车填补了张家口和承德间没有直达高速公路的空白。

作为河北省北部东西走向的重要干线，张承高速公路连接大广高速、京藏高速、二秦高速，东达唐山、秦皇岛两大港口，西连山西、内蒙古能源基地，是东北和西北地区通江达海、东出西联的重要通道。

张承高速公路沿线自然景观丰富，旅游景区密布，有闪电湖、五花草甸、京北第一草原等风景名胜，同时还连接2022年冬奥会举办地崇礼。它的建成通车能有效带动沿线旅游产业发展，促进张承地区扶贫开发。

U441

1009-7716（2016）03-0158-04