基于GA-SVR的水泥分解炉分解率软测量方法
2016-11-24李冰岩张永恒秦石凌
金 星 李冰岩 张永恒 秦石凌 徐 婷
(长春工业大学电气与电子工程学院,长春 130012)
基于GA-SVR的水泥分解炉分解率软测量方法
金 星 李冰岩 张永恒 秦石凌 徐 婷
(长春工业大学电气与电子工程学院,长春 130012)
针对水泥生产企业无法对分解炉分解率进行实时在线检测的情况,结合厂家DCS系统中现有的数据,使用灰色关联分析法观察相关变量与分解炉分解率的关系。利用遗传算法对SVR中的惩罚参数C、核函数核宽g、损失系数ε进行参数寻优,使用寻优结果对分解炉分解率进行SVR软测量建模。不同建模方法间的比较结果表明:使用GA-SVR所建的水泥分解炉分解率模型的预测结果与真实值拟合程度高、测量误差小,能够达到稳定水泥分解炉分解率的目的。
软测量 GA-SVR算法 水泥分解炉
分解炉分解率是新型干法水泥生产中衡量分解炉分解效果的一项重要指标[1]。分解炉分解率的大小和稳定性不仅影响对分解炉的优化控制,对回转窑的熟料烧成也会产生较大影响[2]。目前,分解炉分解率主要通过传统方法进行离线化验,由化验室获得的分解炉分解率周期较长,无法实时反映分解炉运行工况,其滞后性不利于分解炉后期的优化控制[3]。因而,实现对水泥分解炉分解率的实时准确在线检测是水泥优化生产的前提。
软测量技术与机器学习的发展为分解炉分解率的实时在线检测提供了新思路[4]。软测量就是通过工业生产中的可控变量和可测变量,使用机理建模、数理统计建模及神经网络建模等方法计算或估计无法在现阶段实时预测的重要变量。支持向量回归(SVR)是目前机器学习领域的热点,其回归精度高、泛化能力强,在软测量领域有较为优异的表现[5]。笔者通过分析在水泥生产过程中与分解率有关的过程变量,在厂家DCS控制系统的基础上,提出了一种基于GA-SVR的水泥分解炉分解率软测量建模方法。
1 新型干法水泥分解炉窑尾分解率分析
依照水泥生产的工艺流程,按比例配置的生料经四级旋风预热器预热后,在分解炉中进行分解并随气流进入五级旋风预热器,气固分离后进入回转窑窑尾。为保证水泥熟料的质量,分解炉分解率一般介于85%~95%之间[6]。
按照工艺流程,分解炉分解率主要取决于分解炉的工况,三次风温、三次风速、喂煤量及投料量等都会影响分解炉分解率的大小[7]。根据现场调研和水泥厂家DCS中的历史数据,确定以三次风温、分解炉炉内温度、分解炉炉内压力、分解炉出口温度、分解炉出口压力和提升机电流作为分解炉分解率软测量的辅助变量。由厂家DCS系统的大量历史数据确定分解炉分解率的采样时刻,考虑水泥分解炉的滞后性,选取采样前10min内相关过程变量的平均值作为原始数据,剔除相应粗大误差后,最终以获得的218组数据作为样本数据。
所获数据以分解炉分解率序列为参考序列、其余过程变量序列为比较序列,设定分辨系数为0.6进行灰色关联度分析,对原始数据集降维。相关辅助变量及其对应的灰色关联度如下:
分解炉出口温度 0.897 7
提升机电流 0.860 7
分解炉炉内温度 0.813 4
三次风温 0.793 4
分解炉炉内压力 0.760 3
分解炉出口压力 0.742 5
以0.8为本次灰色关联度的阈值,获得本次软测量最终输入数据集合为分解炉出口温度、提升机电流、分解炉炉内温度,输出变量为分解炉分解率。
分解炉出口温度如图1所示。

图1 分解炉出口温度
分解炉炉内温度如图2所示。

图2 分解炉炉内温度
提升机电流如图3所示。

图3 提升机电流
分解炉分解率如图4所示。
2 分解炉分解率软测量模型
2.1SVR理论简介
SVR是支持向量机SVM的回归模式,有坚实的理论依据。对给定的训练资料(x1,y1),…,(xn,yn),xi∈RN,yi∈R,i=1,2,3,…,n。其中x为输入的特征,y为该特征所对应的值。假设给定数据线性可分,对给定样本集,任取ε>0,存在超平面f(x)=
任意点(xi,yi)到超平面的距离不大于:
(1)
为使式(1)最大,回归问题转化为以下优化问题:
(2)
于是,引入松弛变量,并使用拉格朗日乘子法,得到优化问题的对偶形式:
(3)
上述为给定数据可分的情况,若给定数据在原始空间不是线性可分的集合,需使用一个非线性映射将给定数据的特征映射到高维空间,使映射后的特征线性可分[8]:
其中K为有效的核函数。因此,非线性回归的对偶问题转化为:
(4)
求解凸二次规划问题后计算b的值:

(5)

(6)
SVR拟合给定训练数据(x1,y1),…,(xn,yn),xi∈RN,yi∈R,i=1,2,3,…,n所得的回归方程为:
(7)
其中,ai、ai*为拉格朗日算子,b为阈值,K(xj,x)为核函数。
2.2基于遗传算法的ε-SVR的参数优化
遗传算法(GA)无需对所求问题进行了解,通过对算法产生的每个染色体进行评价,让适应度高的染色体更好地繁殖,对每个个体进行优胜劣汰,形成下一代新的种群,再进行下一轮进化。主要步骤如下:
a. 随机产生N个初始串结构数据,每个结构数据是一个个体;
b. 计算群体中每个个体的适应度;
c. 使用复制、交叉、变异操作形成下一代群体;
d. 对新的群体进行步骤b、c的迭代,直到满足停止条件;
e. 获得全局最优解。
依照SVR的推导过程,使用不同的核函数K(xj,x)构建出的SVR模型也不同,笔者使用高斯径向基函数exp(-gamma*|u-v|2)作为核函数,建立SVR软测量模型。为保证SVR模型的准确性,要先确定惩罚系数C、核宽g、损失系数ε。
惩罚系数C与SVR模型的稳定性有关,过大会提高学习精度,但会降低模型的泛化能力;过小会提高泛化能力,但会加大学习误差。核宽g与SVR模型支持向量间联系有关,g越小,模型越复杂[9]。损失系数ε与回归函数对数据样本的不敏感区域的宽度有关,增大ε会减少模型支持向量个数,减小ε提高回归精度增加模型复杂度[10]。
基于遗传算法的ε-SVR的参数优化(C、g、ε)步骤如下:
a. 设置惩罚系数C、核宽g、损失系数ε的范围,产生初始群体。
b. 使用C、g、ε组合下的反映SVR回归性能的均方差(MSE)作为适应度值。
c. 开始遗传操作,计算每组C、g、ε的均方差(MSE),若该组下均方差最小,设定此次C、g、ε参数更新为Cbest、gbest、εbest,否则保留此前的Cbest、gbest、εbest。
d. 停止条件定为最大进化代数。未达到停止条件时,执行步骤c,进行迭代操作;当满足停止条件,即达到进化代数时,此时的Cbest、gbest、εbest即为最优解,按照此惩罚系数C、核宽g、损失系数ε重新对训练集进行SVR建模,作为最终软测量模型。
3 水泥分解炉分解率软测量仿真实验
选取已经预处理的218组有效历史数据中的180组用于构建软测量模型,剩余38组用于验证软测量模型的准确性。采用经遗传算法优化的SVR进行分解炉分解率软测量建模,遗传算法中的参数设置为:最大进化代数200,种群最大数量20,变量维数为3,变量的二进制位数为20,代沟为0.9,参数C的变化范围[Cmin,Cmax],Cmin=0,Cmax=100,参数g的变化范围[gmin,gmax],gmin=0,gmax=100,参数ε的变化范围[εmin,εmax]。经遗传算法选择后C=42.6325,g=23.7862,ε=0.9680。为验证算法的有效性,使用交叉验证CV-SVR与仅使用遗传算法对C、g、ε3个参数和C、g两个参数进行寻优做对照实验。
使用笔者所述遗传算法对SVR的3个参数C、g、ε进行寻优的预测结果如图5所示。

图5 GA-SVR算法软测量预测结果
使用遗传算法仅对SVR参数C、g进行寻优的预测结果如图6所示。使用CV-SVR的预测结果如图7所示。
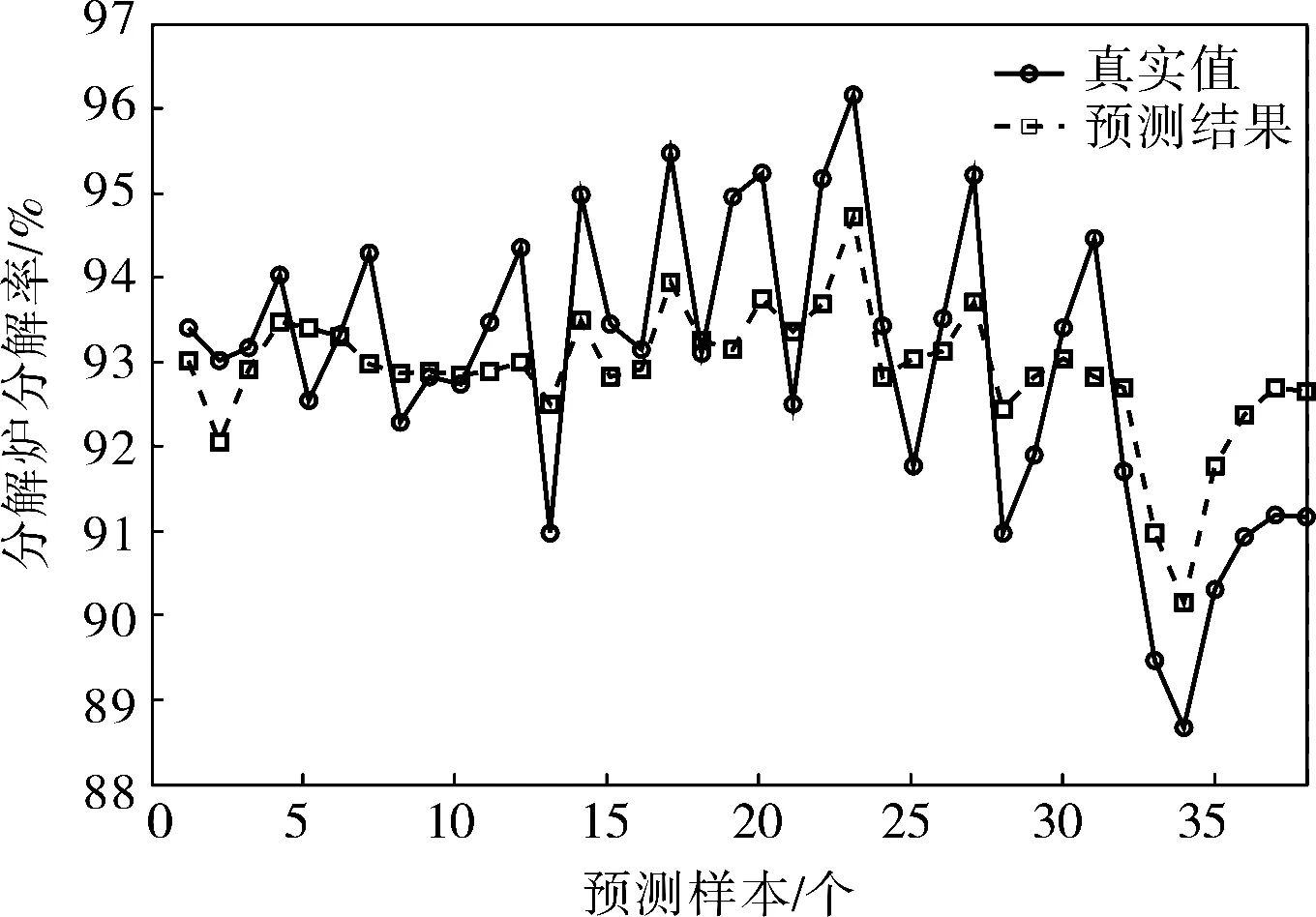
图6 C、g寻优SVR预测结果

图7 CV-SVR预测结果
仿真结果见表1,其中平方相关系数表示与原有数据的接近程度,值越接近于1与原模型越相近。
根据上述仿真结果,使用GA-SVR建立的水泥分解炉分解率软测量模型,准确率较高,具有良好的预测精度和泛化能力。
4 结束语
笔者针对目前新型干法水泥生产中,分解炉分解率无法在线进行测量的问题,使用遗传算法对SVR进行参数寻优,建立了新型干法水泥分解炉分解率软测量模型,具有良好的预测效果。仿真结果表明,本软测量方法能够满足工业要求,对后期水泥生产的优化控制有一定的指导作用。

表1 预测效果对比
[1] 陈全德,兰明章.新型干法水泥技术原理与应用讲座(连载十二)第九讲 回转窑[J].建材发展导向,2005,3(4):22~28.
[2] 孔祥忠.中国水泥工业转变发展方式的思路探讨[J].中国水泥,2012,(1):15~18.
[3] 韩仲琦.中国水泥工业的历史和发展(上)[J].中国水泥,2002,(8):8~12.
[4] 曹宏芳,付忠广,齐敏芳.PSO-SVM软测量方法在火电厂煤质发热量测量中的应用[J].热能动力工程,2014,29(6):731~735.
[5] 顾亚祥,丁世飞.支持向量机研究进展[J].计算机科学,2011,38(2):14~17.
[6] 李帷韬.水泥回转窑烧成状态识别与熟料质量指标软测量的研究[D].沈阳:东北大学,2012.
[7] 王秀莲,孙旭晨,王卓,等.基于局部PSO-LSSVM的水泥f-CaO测量方法研究[J].控制工程,2014,21(6):807~811.
[8] 刘文光,王孝红,于宏亮,等.基于LS-SVM的水泥熟料煅烧过程f-CaO软测量研究[J].控制工程,2008,15(z2):85~88.
[9] 周云龙,王迪.基于PSO-LS-SVM的主蒸汽流量测量[J].化工自动化及仪表,2015,42(4):374~377.
[10] 熊伟丽,徐保国.基于PSO的SVR参数优化选择方法研究[J].系统仿真学报,2006,18(9):2442~2445.
SoftMeasurementMethodforCementFurnaceDecompositionRateBasedonGA-SVR
JIN Xing, LI Bing-yan, ZHANG Yong-heng, QIN Shi-ling, XU Ting
(SchoolofElectricalandElectronicEngineering,ChangchunUniversityofTechnology,Changchun130012,China)
Considering the cement enterprise’s incapability of on-line detecting decomposition rate of the decomposing furnace at real time and basing on existing data from the enterpriser’s DCS system, making use of grey relation analysis method to analyze relationship between correlated variables and furnace’s decomposition rate was implemented, including having genetic algorithm adopted to optimize penalty parameterC, kernel widthgand loss coefficientεin SVR, and then having optimization result based to build SVR soft measurement model for the decomposition rate of the furnace. Comparing the models built through different methods proves that the decomposition rate prediction result of GA-SVR-based cement kiln decomposition model fits the true values well and has smaller errors; and it can stabilize the decomposition rate of the cement furnace.
soft measurement, GA-SVR algorithm, cement decomposing furnace
2016-01-17(修改稿)
吉林省科技厅项目(20150203003SF)
TH865
A
1000-3932(2016)08-0830-05
