高中数学教学中反思能力的培养研究
2016-11-23潘桂兵
潘桂兵
【摘 要】 高中阶段,学生的心智都发展得比较成熟,具有一定的逻辑思辨能力,教师需要把握好其思维特点,在数学教学中系统性地训练其反思能力。
【关键词】 高中数学教学;反思能力;培养研究
高中阶段,学生的心智都发展得比较成熟,具有一定的逻辑思辨能力,教师需要把握好其思维特点,在数学教学中系统性地训练其反思能力。这样才能改变高中数学课堂教学现状,确定学生的主体地位,使其在解答数学题的过程中形成一题多解思维与较强的反思能力,遇到同类题目时可以举一反三,提高解题效率。
一、着重培养学生的观察能力
在课程改革深入进行的背景下,素质教育逐渐得到了重视和推广,这种教育模式要求教师观察学生的生活,全面培养学生的各方面能力,而观察能力则是其中非常重要的一种。高中生处于青春期,对未知事物具有较强的好奇心,教师要把握好这一点,引导其细心观察题目,从而发现问题的突破口,激发强烈的求知欲望。在解题时,教师应向学生渗透数形结合思想,鼓励其扎实掌握直线垂直的概念、两条直线异面、平行、相交的位置关系等数学定理和公理,并且通过与图形相结合,敏锐观察,将数学知识灵活运用于其中,对概念的运用情景进行反复思考,充分发挥想象力,总结图形问题的解决方法。
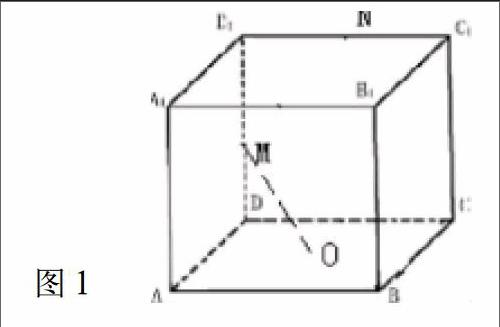
例1:现有一正方体(见图1),底面ABCD的中心为点O,棱D1C1和DD1的中点分别为N和M,那么直线MO( )。
A.不和MN垂直,但与AC垂直
B.是MN与AC的公垂线
C.既不垂直于MN,也不垂直于AC
D.不和AC垂直,但与MN垂直
许多学生在初步审题后,由于观察能力不强,并未准确找到三垂线定理中的射影,所以看到答案A后并未多做考虑就直接选择,认为MO既垂直于MN,又垂直于AC,是MN与AC的公垂线。其实仔细观察再回想定理就能发现,MO不和MN垂直,但与AC垂直,即正确答案为B。
例2:如果直线c和d是在两个不同的平面中,且并无交点,属于异面直线,判断过空间内任意一点Q是否有且只有1个平面同时平行于直线c和d?
学生因为缺乏空间想象力,读题后并未考虑周全,直接认为空间中任意一点Q并未在直线c和d上,判断为真命题。其实当Q在直线c或直线d上时,所作的平面都无法和该直线平行,或者点Q和其中一条直线确定的平面恰好平行于另一条直线,那么同样不符合题目中的结论,所以应判断该题为假命题。
二、引导学生在错误中反思
高中数学知识涉及范围较广,且具有一定的抽象性,学生在解题过程中难免会犯错误,而教师要做的就是教育学生不气馁,不要因一次错误而丧失自信心,要善于从错误中反思,发现原因所在,不断积累经验,避免再次犯同类错误。反思过程中的关键环节就是在解题后反思,对自己采用的解题方法与思维轨迹加以反思。在错题反思中,学生要观察自己的解题步骤,发现具体在哪一步犯错,错误原因(计算过程出错、运用公式错误或者概念理解有误等)。整个反思过程的目的就是让学生对思维过程重新进行梳理,使其通过思维操作,获得解题能力的提升,并且扎实掌握基础性学习内容,如公式、概念、定理等。
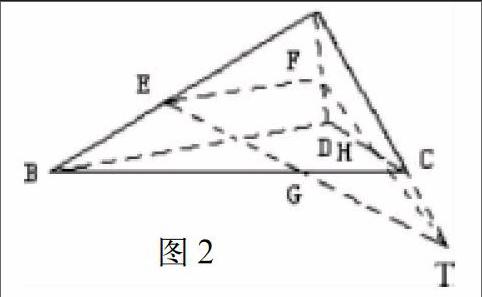
例3:现有空间四边形ABCD(见图2),其两边AD与AB的中点分别为F和E,CD和BC的中点各有一点H和G,求证:直线AC,FH与EG共同交于一点(T)。
许多学生看到题目中的已知条件后,很快得知BD与EF平行,BD=2EF,在后续证明中,依次列出DH/HC=BG/GC=2,BD∥GH,BD=3GH几项推论,由此可知EFGH是梯形,而FH和EG则是梯形的两腰,如果T是二者的交点,因为DH/HC=2,AD与AB的中点分别为F和E,所以FH和AC交于一点,所以直线AC,FH与EG共同交于一点。
这个思维过程的前半部分是正确的,但后半部分分别证明了每两条直线相交,却并未证明三条直线在同一点相交,逻辑性较差。学生在假设梯形的两腰在T点相交后,应从FH、EG分别在平面ACD与ABC上出发,说明T同时属于ACD与ABD两个平面,而这两个平面的交线是AC,所以点T在直线AC上,证明命题正确。
三、培养学生举一反三的能力
高中数学教学中,经常会遇到许多说法不同,但解题方法大致相同的题目,题海战术并不能保障学生掌握其中每道题目的解法,教师应选择经典题目加以训练,培养学生的反思能力,使其能举一反三,提高解题效率。
例4:f(x) =√ax2+4x+2 的定义域是R,那么a的取值范围的多少?
原函数的定义域为R,且式子ax2+4x+4 在根号内,所以可知在R上ax2+4x+4 >0是恒成立的,因此a>0,同时要满足二次函数的最小值,即(8a-16)/4a>0,所以a>2。
当学生掌握该题的解法后,教师可以改变出题形式,比如要求学生求多项式ax2+4x+4的对数,变成新的题目:函数f(x) =log3√ax2+4x+2的定义域是R,那么a的取值范围的多少?而解题方法其实和例4相同,前一道题主要考察定义域的概念、根号的定义与意义,而后一道题则考察log函数的定义。学生在深入理解有关数学基础概念的情况下,很快就能理清思路,得出答案。教师要引导学生多反思解题过程,通过强化训练,掌握概念的意义并将其灵活运用于数学题目的解答中。另外,在改变后的题目中,教师还可以将根号去掉,考察学生对换元法的掌握情况,通过变换题目训练学生的多种能力。
在高中数学教学中,教师要有效培养学生的数学能力和反思能力,从而使其学习效率与解题能力提高。与此同时,较强的反思能力并不意味着要一直反思,或者越多越好,而是要学生自行发现并解决问题。学生要善于发现反思缺口,通过探索解决数学问题后,就要适时结束反思过程,避免思维进入死胡同,为其今后的学习奠定良好基础。
