理清概念掌握运算透视考点

贾芸芸

理清概念掌握运算透视考点

贾芸芸

在初中数学中，“数与式”是“数与代数”领域的重要基础内容，它包括：有理数、实数、代数式、整式、分式等.这部分内容有如下的突出特点：知识点多，技能性强，体现转化思想和类比方法多，因此是中考重要考点之一，一般以选择题、填空题和简单的解答题出现.中考考查的重点是概念，运算量不大.现把2015年全国各地数与式中常见的考点归纳如下.

考点一：相反数、绝对值、倒数的相关概念

例1（2015·黔南州）下列说法错误的是（）.

A.-2的相反数是2

C.（-3）-（-5）=2

D.-11，0，4这三个数中最小的数是0

【考点】相反数；倒数；有理数的减法；有理数大小比较.

【分析】根据相反数的概念、倒数的概念、有理数的减法法则和有理数的大小比较进行判断即可.

解：-2的相反数是2，A正确；

（-3）-（-5）=-3+5=2，C正确；

-11，0，4这三个数中最小的数是-11，D错误.故选D.

【点评】本题考查的是相反数的概念、倒数的概念、有理数的减法法则和有理数的大小比较，掌握相关概念和法则是解题的关键.

考点二：无理数的概念

A.4B.2C.1D.3

【考点】无理数.

【分析】掌握无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数，结合题意判断即可.

【点评】此题主要考查了无理数的定义，熟记无理数的三种形式是解题关键.

考点三：实数与数轴

例3（2015·枣庄）实数a，b，c在数轴上对应的点如图1所示，则下列式子中正确的是（）.

图1

A.ac＞bc

B.a-b=a-b

C.-a＜-b＜c

D.-a-c＞-b-c

【考点】实数与数轴.

【分析】先根据各点在数轴上的位置比较其大小，再对各选项进行分析即可.

解：∵由图1可知，a＜b＜0＜c，

∴ac＜bc，故A选项错误；

∵a＜b，∴a-b＜0，∴a-b=b-a，故B选项错误；

∵a＜b＜0，∴-a＞-b，故C选项错误；

∵-a＞-b，c＞0，∴-a-c＞-b-c，故D选项正确.故选D.

【点评】本题考查的是实数与数轴，熟知数轴上各点与实数是一一对应关系是解答此题关键.

例4（2015·资阳）如图2，已知数轴上的点A、B、C、D分别表示数-2、1、2、3，则表示数的点P应落在线段（）.

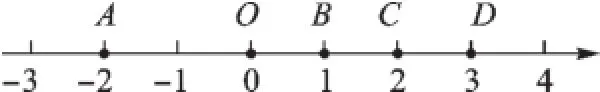
图2

A.AO上B.OB上

C.BC上D.CD上

【考点】估算无理数的大小；实数与数轴.

故选B.

考点四：科学记数法

例5（2015·盐城）火星与地球的距离约为56 000 000千米，这个数据用科学记数法表示为__________千米.

【考点】科学记数法.

【分析】科学记数法的表示形式为a×10n的形式，其中1≤a＜10，n为整数.确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同.当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数.

解：将56 000 000用科学记数法表示为5.6×107.故答案为：5.6×107.

【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式，其中1≤a＜10，n为整数，表示时关键要正确确定a的值以及n的值.

考点五：数的开方与二次根式

例6（2015·南京）4的平方根是______；4的算术平方根是______.

【考点】算术平方根；平方根.

【分析】如果一个非负数x的平方等于a，那么x是a的算术平方根，由此即可求出结果.

解：4的平方根是±2；4的算术平方根是2.故答案为：±2；2.

【点评】此题主要考查了平方根和算术平方根的概念，算术平方根易与平方根的概念混淆而导致错误.

A.x≠1B.x≥1

C.x＞1D.x≥0

【考点】二次根式有意义的条件.

【分析】先根据二次根式有意义的条件列出关于x的不等式，求出x的取值范围即可.

【点评】本题考查的是二次根式有意义的条件，熟知二次根式具有非负性是解答此题的关键.

【考点】非负数的性质：算术平方根；非负数的性质：偶次方.

【分析】根据非负数的性质可求出m、n的值，进而可求出（m+n）5的值.

解：由题意知，m，n满足（m-1）2+=0，∴m=1，n=-2，∴（m+n）5=（1-2）5=-1.故答案为：-1.

【点评】此题主要考查了非负数的性质，初中阶段有三种类型的非负数：①绝对值；②偶次方；③二次根式（算术平方根）.当它们相加和为0时，必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.

考点六：代数式、整式、分式

例9（2015·扬州）若a2-3b=5，则6b-2a2+2015=_______.

【考点】代数式求值.

【分析】首先根据a2-3b=5，求出6b-2a2的值是多少，然后用所得的结果加上2015即可.

解：6b-2a2+2015=-2（a2-3b）+2015=-2× 5+2015=-10+2015=2005.

答案：2005.

【点评】此题主要考查了代数式的求值问题，采用代入法即可，要熟练掌握.题型简单总结有以下三种：①已知条件不化简，所给代数式化简；②已知条件化简，所给代数式不化简；③已知条件和所给代数式都要化简.

例10（2015·本溪）下列运算正确的是（）.

A.5m+2m=7m2

B.-2m2·m3=2m5

C.（-a2b）3=-a6b3

D.（b+2a）（2a-b）=b2-4a2

【考点】幂的乘方与积的乘方；合并同类项；单项式乘单项式；平方差公式.

【分析】A.依据合并同类项法则计算即可；B.依据单项式乘单项式法则计算即可；C.依据积的乘方法则计算即可；D.依据平方差公式计算即可.

解：A.5m+2m=（5+2）m=7m，故A错误；

B.-2m2·m3=-2m2+3=-2m5，故B错误；

C.（-a2b）3=-a6b3，故C正确；

D.（b+2a）（2a-b）=（2a+b）（2a-b）=4a2-b2，故D错误.故选C.

【点评】本题主要考查的是整式的计算，掌握合并同类项法则、单项式乘单项式法则、积的乘方法则以及平方差公式是解题的关键.

A.2或-1B.0

C.2D.-1

【考点】分式的值为零的条件.

【分析】分式的值为0的条件是：（1）分子为0；（2）分母不为0.两个条件需同时具备，缺一不可.据此可以解答本题.

解：由题意可得：x-2=0且x+1≠0，

解得x=2.故选C.

【点评】此题主要考查了分式值为零的条件，关键是掌握分式值为零的条件是分子等于零且分母不等于零.注意：“分母不为零”这个条件不能少.

考点七：因式分解

例12（2015·毕节）下列因式分解正确的是（）.

A.a4b-6a3b+9a2b=a2b（a2-6a+9）

B.x2-x+

C.x2-2x+4=（x-2）2

D.4x2-y2=（4x+y）（4x-y）

【考点】因式分解：运用公式法；提公因式法.

【分析】原式各项分解得到结果，即可做出判断.

解：A.原式=a2b（a2-6a+9）=a2b（a-3）2，错误；

C.原式不能分解，错误；

D.原式=（2x+y）（2x-y），错误，故选B.

【点评】此题考查了因式分解的运用公式法以及提公因式法，熟练掌握因式分解的方法是解本题的关键.

考点八：数字规律探索

例13（2015·临沂）观察下列关于x的单项式，探究其规律：x，3x2，5x3，7x4，9x5，11x6，…，按照上述规律，第2015个单项式是（）.

A.2015x2015B.4029x2014

C.4029x2015D.4031x2015

【考点】单项式；规律型.

【分析】系数的规律：第n个对应的系数是2n-1；

指数的规律：第n个对应的指数是n.

解：根据分析的规律，得

第2015个单项式是4029x2015.故选C.

【点评】此题考查单项式问题，分别找出单项式的系数和次数的规律是解决此类问题的关键.

（作者单位：江苏省淮安外国语学校）