基于瞬变电磁矩变换的快速三维反演方法

饶丽婷，武欣，吴超，张晓娟，方广有

1 中国科学院电磁辐射与探测技术重点实验室，北京 1001902 中国科学院大学，北京 100049



基于瞬变电磁矩变换的快速三维反演方法

饶丽婷1,2，武欣1,2，吴超1,2，张晓娟1，方广有1

1 中国科学院电磁辐射与探测技术重点实验室，北京 1001902 中国科学院大学，北京 100049

瞬变电磁法的严格三维反演计算复杂、占用资源多，在普通计算机上难以实现.本文引入瞬变电磁矩变换的概念，提出一种快速三维反演方法.该方法基于阻性限制(resistive limit)特性，建立包含异常体的三维大地的一阶矩响应正演算法，根据不同约束条件，选择优化的最速下降法实现瞬变电磁快速三维反演.文中通过含异常体的三维大地正演一阶矩与仿真数据一阶矩的对比，验证了快速三维正演算法的有效性，之后在不同约束条件下，利用优化的最速下降法实现了对含噪声的仿真瞬变电磁数据的快速三维反演.结果表明，该方法能够在普通计算机上短时间内较为准确地反演出地下异常体的体积和位置，在瞬变电磁数据的实时解释工作中具有良好的应用前景.

瞬变电磁法；瞬变电磁矩变换；阻性限制；快速三维反演

1 引言

瞬变电磁法是一种建立在电磁感应原理上的时间域人工源电磁探测方法(Nabighian，1988)，广泛应用于矿产资源勘探、地下水探查、地质调查与地质填图等领域(Fitterman and Stewart，1986；Meju et al.，2002；He et al.，2012；嵇艳鞠等，2013；Xue et al.,2013;殷长春等，2015).瞬变电磁反演建立在正演算法基础上，由于高维正演算法的复杂性,高维反演问题尚未妥善解决(薛国强等，2008；Yin et al.,2015).Cox等(2012)采用积分方程法实现了航空瞬变电磁的正反演，Oldenburg等(2013)利用有限元法实现了瞬变电磁的三维正反演，然而这些严格三维反演方法受限于复杂的三维正演算法，数据量巨大，占用资源过多，在普通计算机上几乎无法运行，故以其为基础的严格三维反演运算速度缓慢，不能真正投入实际应用.

为了使三维反演易于实现，必须尽量压缩数据量并简化正演算法，因此本文引入瞬变电磁矩变换.瞬变电磁矩变换是Smith和Lee (2002)在阻性限制和感性限制的基础上扩展而来，其中，阻性限制定义为当频率趋近于零时频域瞬变磁场斜率的幅度值(Grant and West,1965)，该限制等于时域中理想负阶跃响应(磁场)的面积积分即瞬变电磁一阶矩.

Smith (2000)利用阻性限制对航空瞬变电磁数据成像，发现图像中包含off-time观测方式无法探测的地电特征；Reid和Macnae (2002)利用阻性限制对数据量庞大的航空电磁勘探数据建模，简化了耗时巨大的航空数据解释处理工作.电磁场在传播过程中，当满足阻性限制条件时，其已充分穿透目标体，目标体内部感应作用可忽略.故可将目标体网格化，通过几何耦合因子与时间常数乘积计算各目标体微元的响应，对所有微元响应进行线性叠加可得到目标体的总响应(King,1997).

由以上可知，利用瞬变电磁一阶矩变换不仅可以大幅压缩处理数据量，而且能够简化目标体响应计算，因此本文基于瞬变电磁矩变换，提出一种快速三维反演方法.首先，以瞬变电磁感性限制和阻性限制概念为基础，引入瞬变电磁矩变换定义；然后以矩形回线源为例，推导了点导电球体以及均匀半空间的一阶矩响应，并在此基础上建立了含异常体大地的一阶矩响应的近似三维正演算法；之后，采用含松弛因子的优化最速下降法作为迭代算法，并结合约束条件，阐述快速三维反演的原理；最后，在不同约束条件下，对含噪声的仿真瞬变电磁数据实施了快速三维反演，结果表明，该方法能够在普通计算机条件下短时间内较为准确地反演出地下异常体的体积和位置，本文的研究成果可应用于瞬变电磁数据的实时解释工作中.

2 瞬变电磁矩变换

对于理想负阶跃响应，可由一系列指数函数求和表示(Stolz and Macnae,1998)：

(1)

其中Ai和τi分别表示第i个指数函数的幅度和时间常数.在频域，负阶跃响应表示为

(2)

当频率趋于无穷大时，负阶跃响应达到感性限制IL(Inductive Limit):

(3)

感性限制时，感应电流仅存在于目标体表面以抵抗一次场法向分量，此时，电流没有穿透到目标体内部，感性限制仅与发射接收的几何信息有关，与目标体的电导率无关，目标体感性限制可表示如下：

(4)

上式中，Gk为几何耦合因子，仅与发射接收的几何信息有关.

当频域负阶跃响应的斜率趋近于零频时，达到阻性限制RL(Resistive Limit):

(5)

阻性限制时，电磁场已经充分穿透目标体，当ω→0，磁场变化近乎为零，目标体内部感应作用可忽略.此时，可将目标体网格化，通过几何耦合因子与时间常数的乘积计算单个微元响应，将所有微元响应线性叠加得到目标体响应，表示如下：

(6)

上式中，τk为时间常数，与微元的电导率有关.

基于阻性限制和感应限制的概念，Smith和Lee (2002)提出了瞬变电磁矩变换，定义如下:

(7)

即脉冲响应与时间加权的积分，其中g(t)表示脉冲响应，n表示时间加权的阶数.脉冲响应可由负阶跃响应表示如下：

(8)

将矩变换采用磁场时间导数定义，可表示为

(9)

当n=0时，零阶矩等于感性限制，此时零阶矩响应与导体的电导率无关，仅仅与发射接收的几何信息有关；当n=1时，一阶矩等于阻性限制，此时目标体一阶矩响应可由其所有微元响应线性叠加，每个微元响应分解成几何耦合因子与时间常数的乘积，时间常数与导体的电导率相关；当n取更高阶时，高阶矩更加强调晚期信号的加权.目前，还没有明确的物理意义，从定义来看，高阶矩适合探测更深部的异常体，然而对晚期信号加权也会放大噪声，并且目标体高阶矩响应计算更加复杂.综上，本文将采用瞬变电磁一阶矩，首先建立含异常体的大地的三维正演理论.

3 近似三维正演理论

3.1 点导电球体的一阶矩

图1 导电球体几何示意图Fig.1 The geometric configuration of the conducting sphere

Grant和West(1965)、Kaufman(1978)等先后推导了导电球体的全时域磁场响应，对时域磁场作一阶矩变换后，导电球体响应的表达式更加简化(Smith and Lee,2001)，如图1所示，经过矩形回线源激励后，自由空间中点导电球体的一阶矩为

(10)

在自由空间中，半径为a和电导率为σ的圆球的时间常数定义为

(11)

将(10)式中时间常数外的部分作为几何耦合因子，表示为

(12)

根据毕奥萨伐尔定律，一次场B0可表示为

(13)

(14)

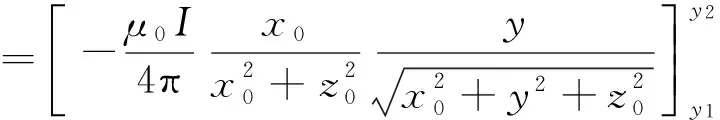
(15)

沿x方向线电流源积分得到一次场的y分量和z分量，表达式分别为

(16)

(17)

沿回线各个方向的线电流定积分并求和，可得到总一次场B0.

3.2 均匀半空间的一阶矩

设一个矩形发射线框置于均匀半空间表面，如图2所示，直角坐标系原点位于线框中心，均匀半空间任意接收点处二次场的垂直磁场表达式为(Schaa and Fullagar,2012)：

图2 矩形回线源装置示意图Fig.2 The geometry of a rectangular loop on the surface of half space

(18)

上式中，G(x,y,t)为单位电流元激励的垂直磁场响应，

x1=XE-XR，x2=XW-XR，y1=YN-YR，y2=YS-YR.G(x,y,t)表达式为

(19)

(20)

(21)

上式中，当t→0时，中括号部分的表达式等于零，同时，尾部的积分可进一步化简，因此，沿y方向的线电流激励形成的一阶矩响应表达式为

(22)

上式表示从端点(x,y1)到(x,y2)定积分.在矩形线框源激励下，均匀半空间的总一阶矩等于四条边框方向的一阶矩之和.

3.3 三维正演理论

(23)

微元的几何耦合因子可通过等体积导电球体的几何耦合因子近似，表示如下：

(24)

微元的时间常数τk同样可由相同电导率和体积的导电球体时间常数近似，可得

(25)

其中，L为立方体微元的边长.

4 三维快速反演原理

4.1 优化最速下降法

TEM测量数据中包含背景响应和异常体响应，为了简化反演问题，首先从N个测量数据一阶矩中剔除背景一阶矩得到异常体响应的参考一阶矩d=(d1,d2,…,dN)T，令实测数据一阶矩的误差为q=(q1,q2,…,qN)T，将可能存在异常的区域划分为K个立方体微元，微元时间常数为τ=(τ1,τ2,…,τK)T，令异常区域的理论一阶矩为c=(c1,c2,…,cN)T.根据三维近似正演模型，第n个接收点处异常区域的理论一阶矩cn可以表示为

(26)

上式中，Gnk为第n个接收点处第k个微元的几何耦合因子.由于数据误差的存在，根据加权最小二乘法的原理，定义异常区域的理论一阶矩与参考一阶矩的拟合差目标函数为

(27)

对于这种线性反演问题，选择最速下降法进行迭代优化.在迭代过程中，令τi代表第i次迭代起始时最优时间常数矢量，经过迭代后，第i+1次起始时最优化时间常数矢量τi+1=τi+δτi，δτi为时间常数的扰动参数矢量.在反演迭代过程中，最速下降法以负梯度方向作为下降方向，因此，δτi可表示为

(28)

下面推导每次迭代中步长αi的大小，第i+1次迭代目标函数的表达式如下：

(29)

(30)

将式(30)代入式(29)，这样，(29)式可写为

(31)

其中，

(32)

(33)

(34)

为了使L(τi+1)取得最小值，有

(35)

将式(31)和式(33)代入到式(35)，求导可得

(36)

由上式可求得

(37)

最速下降法虽然简单，计算快，无矩阵求逆，但是收敛速度慢，尤其是当越接近最优解时，收敛速度进一步放慢.最速下降法收敛性慢的根本原因是最优化步长的选择，而不是负梯度下降方向(Raydan and Svaiter,2002).为了加快收敛速度，本文引入松弛因子ri对步长做调整，每次迭代中线性搜索当前最优松弛因子，此时δτi为

(38)

4.2 约束条件

由于三维反演问题的欠定性，直接反演一般无法得到合理结果，为了促使反演结果贴近真实地下结构，本文给出两种约束条件：

(1) 电导率加权：起始时间常数为零，根据视电导率深度图(conductivity-depth-imaging,CDI)对相应位置处微元赋予加权值，反演过程中，所有微元的时间常数限制为正值.

加权值由CDI决定，分布于0和1之间，第k微元相应的加权值为

(39)

其中，σk为第k微元相应的视电导率值，σmax为整个CDI中最大的视电导率.电导率加权使CDI中大电导率区域占主导作用，减弱小电导率区域的几何耦合因子影响.需要注意的是，电导率加权值依赖CDI，如果CDI存在虚假异常，可能反演不出合理结果.

(2) 深度加权：起始时间常数为零，对不同深度的微元赋予加权值，反演过程中，所有微元的时间常数限制为正值.

由于浅层几何耦合因子Gk较大，为了减弱浅层耦合因子的影响并促使反演朝着较深层变化(Oldenburg and Li,2005)，根据经验函数计算深度加权值，函数定义如下：

(40)

上式中，zk为第k微元的深度，s0为斜率因子，d0为参考深度.s0影响加权值的增长速度，斜率因子越小，加权值随着深度变化增长越慢；设定d0相当于引入了表面层，在参考深度以上的加权值为零.不同d0和s0对应的加权值变化曲线如图3所示.

图3 不同斜率因子s0和参考深度d0的加权值变化曲线Fig.3 Depth weights for various s0 and d0factors

实际反演中，斜率因子s0和参考深度d0的选择不是固定的.如果异常体分布在较深处，则应选择较小的斜率因子，参考深度d0的引入是为了减弱发射线圈下方浅层的较强几何耦合因子的影响，d0可通过CDI中低电导率逐渐变化到高电导率的分界位置决定.经验表明，CDI中电导率最高处对应的加权值为0.5时，是斜率因子的最优值.

4.3 快速三维反演流程图

图4给出了快速三维反演的总体流程图.

图4 快速三维反演总体流程图Fig.4 The flowchart of rapid 3D inversion procedure

5 三维正演验证与反演实现

5.1 瞬变电磁一阶矩验证

从瞬变电磁矩变换的定义可以看出，一阶矩的积分时间范围是从零到无穷大，而实测数据是有限时间内.为了得到实测数据的一阶矩，需补齐实测数据时间外积分，因此，实测数据一阶矩可通过下式求解：

(41)

其中，t1和tn分别表示实测数据的起始时间窗和截止时间窗，σ1和σn分别表示t1和tn时间处的视电导率，头部表示从0到t1时间内磁场积分，中部表示实测数据的积分，尾部表示从tn到∞时间内的磁场积分.头部通过(22)式均匀半空间的完整一阶矩减去(21)式中从t1到∞的数值积分求得；尾部直接对(21)式从tn到∞数值积分求得；中部通过对实测数据B(t)三次样条插值得到拟合函数，然后对拟合函数在t1和tn时间内数值积分.

图5给出了电导率为1 mS·m-1和200 mS·m-1的均匀半空间上垂直磁场一阶矩的计算结果，图中发射源为矩形线框回线，中心位于(0E,0N)，其中，E，N分别代表东西向、南北向，线框大小为250E×250N，发射电流为1A，图中测线在0N方位从-500E到500E，测线上接收点间距为50 m，仿真数据的时间窗从0.001 ms到100 ms.其中理论一阶矩采用(21)式计算，理论中部是利用(21)式和(22)式计算出时间窗范围内的磁场积分，仿真中部即对仿真数据三次样条插值后求定积分，拼接一阶矩是仿真中部加上理论计算的头尾一阶矩，即(41)式的计算方法.这里，仿真数据是采用Gaver-Stehfest变换对任意形状发射回线频域响应求时间域响应得到(齐有政等，2013).

由图5可以看出，理论一阶矩与拼接一阶矩完全吻合，理论中部与仿真中部同样也在每个数据点上显著地一致.图5验证了(21)式中均匀半空间的理论一阶矩的正确性，同时也说明(41)式对实测数据进行拼接头部和尾部得到完整一阶矩的可行性.

5.2 近似三维正演算法验证

EMIT Maxwell软件的Marco算法模块基于三维积分方程，可计算层状大地中含多个棱柱体异常目标的瞬变电磁响应(Xiong and Tripp,1995).本文利用该算法模块的结果验证文中所提三维正演算法的有效性.

根据Marco算法模块的特性，建立验证近似三维正演算法的计算模型，该模型三维示意图如图6所示，在电导率为1 mS·m-1的均匀大地背景中放置电导率为1 S·m-1的高导异常体，该异常体大小为

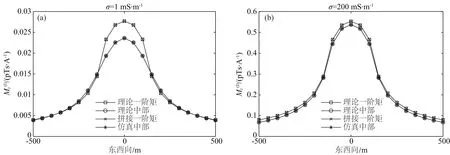
图5 均匀大地上垂直磁场的一阶矩.(a)电导率为1 mS·m-1；(b)电导率为200 mS·m-1Fig.5 First order vertical TEM moment of a half space.(a) Conductivity of 1 mS·m-1;(b) Conductivity of 200 mS·m-1

图6 仿真计算模型的三维几何示意图Fig.6 3D geometry of model for simulated calculation

图7 仿真模型俯视图与发射源位置及测线布置Fig.7 Top view of the simulated model and position of the transmitting source and the survey line arrangement

600E×600N×300Z，上表面中心的坐标为(-100E,0N,-300Z)，其中，Z代表深度向，矩形线框发射源的中心位于(0E,0N,0Z)，线框大小为450N×450E.图7是发射线框和测线分布平面图，如图所示，在南北方位上从-500N到500N分布11条测线，测线间距为100 m，每条测线的走向从-500E到500E，均匀分布有21个接收点.

利用Marco算法模块仿真磁场垂直分量的数据，发射电流波形为双极性方波，发射电流1A，共30个接收时间窗口，时间窗口范围从0.1 ms到53 ms.

仿真计算完成后，将时间域磁场数据通过5.1节中的方法转换为一阶矩，这里是正演验证，计算头部和尾部的积分时，直接采用背景介质的设定电导率.由于异常体处于传导性环境中，无法直接采用自由空间中时间常数公式计算其时间常数，因此，本文采用经验的时间常数分析方法，该方法通过对磁场晚期信号进行指数函数拟合，得出异常体的时间常数估值为1.6 ms.将平板剖分成108000个边长为10 m的立方体微元，经过正演计算后，在各条测线上垂直分量一阶矩曲线如图8所示，由于对称性，只显示了0N到-500N测线上的结果，可以看出，Marco仿真数据一阶矩与近似三维正演的理论一阶矩在每条测线上都有明显的一致性，同时，RMS也显示了仿真数据一阶矩与理论一阶矩之间只有较小的误差.

5.3 快速三维反演实现

5.3.1 预处理工作

采用5.2节中的计算模型进行反演，参考图4的反演流程图，首先进行预处理工作，设定异常区域范围为-500E到500E，-500N到500N，-1500Z到-100Z，将异常区域划分成89600个边长为25 m立方体单元，根据发射接收及微元的几何参数计算几何耦合因子矩阵G，矩阵大小为231×89600，需要注意的是，该几何耦合因子矩阵与测量数据无关，因此，该矩阵可在测量之前完成计算，在反演中作为一个加载数据项.

对Marco仿真磁场数据形成CDI，图9是在0N方位上经过插值后的CDI切面图，如图所示，高电导率区域顶部区域一定程度反应了异常体的位置，然而高电导率区域的底部位置远远超出了实际异常体，该插值CDI可以用于计算电导率加权值，而且在实地测量数据反演中，CDI可作为参考，验证反演结果的可靠性；从中心接收点的CDI中读取t1和tn时间处的视电导率σ1和σn，利用(41)式计算出仿真数据一阶矩，将仿真数据一阶矩中加入5%高斯白噪声作为实测一阶矩，引入的数据误差为0.0035pTs/A，从CDI中估算出背景介质的电导率，之后计算出背景一阶矩，从实测一阶矩中减去背景一阶矩得到异常区域的参考一阶矩.

图8 仿真数据一阶矩、背景一阶矩、正演一阶矩在各条测线上曲线图Fig.8 TEM Bz-moments of synthetic data,background,forward theoretical response at a range of Northings

图9 CDI切面图Fig.9 Conductivity-depth sections

5.3.2 无约束反演

时间常数的初值设定为零，在反演过程中，时间常数无任何约束，初始拟合差为69.6，耗时24 s后达到收敛，反演的时间常数切面图如图10所示，浅层较强的几何耦合因子使反演的异常区域贴近地面，同时，时间常数出现负值，可见反演结果并不能反映异常体的真实地电结构，因此，为了使反演贴近实际地下结构，反演过程中，设定约束条件是非常必要的.

5.3.3 电导率加权反演

利用插值CDI得到相应的电导率加权值，加权值切面图如图11a所示，根据电导率约束条件，反演出最优时间常数，其切面图如图11b所示，与无限制条件的反演结果不同，电导率加权的反演结果中，高时间常数区域局限于实际异常体的体积范围内，更加准确反映地下目标的位置和体积.

图10 无约束反演时间常数切面图Fig.10 Recovered time constant model based on the unconstrained starting model

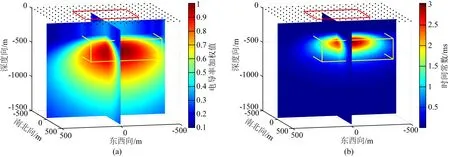
图11 (a) 电导率加权值切面图;(b) 反演时间常数切面图Fig.11 (a) The sections of conductivity weights;(b) The same sections of the recovered time constant model

5.3.4 深度加权反演

采用两种深度加权参数进行反演，第一种参数为s0=0.004，d0=250，对应的深度加权值切面图和反演时间常数切面图为图12a和12b.第二种参数为s0=0.004，d0=150，对应的深度加权切面图和反演时间常数切片图为图13a和13b.其高时间常数区域与异常体的位置和体积较好的吻合，第二种参数反演出高时间常数区域较第一种情况扩大一些，且高时间常数区域的顶部比实际平板位置高一些，这是由于第二种参数的参考深度d0小一些，使异常体顶部的浅层耦合因子影响比较大.因此，在反演中合理设置深度加权参数是非常重要的.

5.3.5 快速三维反演效率

表1给出了分别采用传统最速下降法和优化最速下降法的反演效率对比.观察表1，相比严格三维反演方法，本文中三维反演方法无论采用传统还是优化最速下降法，都非常高效地得到反演结果.同时，经过松弛因子优化的最速下降法，收敛速度可提高几十倍甚至百倍，反演经过几秒到几十秒就可得到收敛结果.

表1 传统最速下降法和改进最速下降法反演效率对比

6 总结

本文提出了一种基于瞬变电磁矩变换的快速三维反演方法.文中应用瞬变电磁一阶矩变换，将任意接收点处的一道瞬变电磁数据压缩成了点数据，数据量的大幅压缩不仅加速了反演的处理速度，同时也使三维反演能够在普通计算机上实现；在阻性限制约束下，目标体内部感应作用可以忽略，可将目标体网格化，通过几何耦合因子与时间常数乘积计算各目标体微元的响应，对所有微元响应进行线性叠加可得到目标体的总响应，基于此特性，建立了一种近似简化的三维正演算法，将此正演算法应用到三维反演中，加速了三维反演的速度；在反演问题的优化迭代算法中，引入松弛因子，改进了传统的最速下降法，使收敛速度进一步提高；为了促使反演结果贴近真实地下结构，文中给出了两种约束条件，实际应用中可灵活运用.最后需要强调的是，本文虽然以矩形回线源为例推导了三维正演算法，但是本文所提方法对瞬变电磁的发射源没有限制，既适用于电性源，也适用于磁性源，同时，该方法不仅可用于地面，也可用于航空或者半航空.

图12 深度加权参数s0=0.004，d0=250(a) 深度加权值切面图;(b) 反演时间常数切面图.Fig.12 Weight with parameters s0=0.004 and d0=250(a) The sections of depth weights;(b) The same sections of the recovered time constant model.

图13 深度加权参数s0=0.004,d0=150(a) 深度加权值切面图;(b) 反演时间常数切面图.Fig.13 Weight with parameters s0=0.004 and d0=150(a) The sections of depth weights;(b) The same sections of the recovered time constant model.

三维瞬变电磁反演方法是国内外地球物理方向的重要研究热点之一，复杂的严格三维反演具有各种技术条件限制，使其无法投入实际应用中.本文在普通计算机上实现了一种近似的快速三维反演，结果表明，该方法在瞬变电磁实时解释工作中具有良好的应用前景.

致谢 作者向中国科学院电子所李光博士、王友成博士在论文准备过程中提供的帮助致谢.

Cox L H,Wilson G A,Zhdanov M S.2012.3D inversion of airborne electromagnetic data.Geophysics,77(4):WB59-WB69.

Fitterman D V,Stewart M T.1986.Transient electromagnetic sounding for groundwater.Geophysics,51(4):995-1005,doi:10.1190/1.1442158.

Grant F S,West G F.1965.Interpretation theory in applied geophysics.New York:McGraw-Hill Book Co.

He Z X,Zhao Z,Liu H Y,et al.2012.TFEM for oil detection:Case studies.The Leading Edge,31(5):518-521.

Ji Y J,Wang Y,Xu J,et al.2013.Development and application of the grounded long wire source airborne electromagnetic exploration system based on an unmanned airship.Chinese Journal of Geophysics (in Chinese),56(11):3640-3650,doi:10.6038/cjg20131105.

Kaufman A.1978.Frequency and transient responses of electromagnetic fields created by currents in confined conductors.Geophysics,43(5):1002-1010.King A.1997.Inversion of localized electromagnetic anomalies [Ph.D.thesis].Australia:Macquarie University.

Meju M A.2002.Geoelectromagnetic exploration for natural resources:Models,case studies and challenges.Surveys in Geophysics,23(2-3):133-206.

Nabighian M N.1988.Electromagnetic methods in applied geophysics-theory volume I.Society of Exploration Geophysicists,313-503.

Oldenburg D W,Li Y G.2005.Inversion for applied geophysics:A tutorial.∥Butler D K ed.Near-Surface Geophysics.SEG,89-150.

Oldenburg D W,Haber E,Shekhtman R.2013.Three dimensional inversion of multisource time domain electromagnetic data.Geophysics,78(1):E47-E57.

Qi Y Z,Huang L,Zhang J G,et al.2013.Study on the electromagnetic fields of an extended source over layered models.Acta Physica Sinica (in Chinese),62(23):234201.

Raydan M,Svaiter B F.2002.Relaxed steepest descent and cauchy-barzilai-borwein method.Computational Optimization and Applications,21(2):155-167.

Reid J E,Macnae J C.2002.Resistive limit modeling of airborne electromagnetic data.Geophysics,67(2):492-500.

Schaa R,Fullagar P K.2012.Vertical and horizontal resistive limit formulas for a rectangular-loop source on a conductive half-space.Geophysics,77(1):E91-E99.

Smith R S.2000.The realizable resistive limit:A new concept for mapping geological features spanning a broad range of conductances.Geophysics,65(4):1124-1127.

Smith R S,Lee T J.2002.The moments of the impulse response:A new paradigm for the interpretation of transient electromagnetic data.Geophysics,67(4):1095-1103.

Smith R S,Lee T J.2001.The impulse-response moments of a conductive sphere in a uniform field,a versatile and efficient electromagnetic model.Exploration Geophysics,32(2):113-118.

Stolz E M,Macnae J.1998.Evaluating EM waveforms by singular-value decomposition of exponential basis functions.Geophysics,63(1):64-74.

Xiong Z H,Tripp A C.1995.A block iterative algorithm for 3-D electromagnetic modeling using integral equations with symmetrized substructures.Geophysics,60(1):291-295.

Xue G Q,Li X,Di Q Y.2008.Research progress in TEM forward modeling and inversion calculation.Progress in Geophysics (in Chinese),23(4):1165-1172.

Xue G Q,Cheng J L,Zhou N N,et al.2013.Detection and monitoring of water-filled voids using transient electromagnetic method:A case study in Shanxi,China.Environmental Earth Sciences,70(5):2263-2270,doi 10.1007/s12665-013-2375-2.

Yin C C,Ren X Y,Liu Y H,et al.2015.Review on airborne electromagnetic inverse theory and applications.Geophysics,80(4):W17-W31.

Yin C C,Zhang B,Liu Y H,et al.2015.Review on airborne EM technology and developments.Chinese Journal of Geophysics (in Chinese),58(8):2637-2653,doi:10.6038/cjg20150804.

附中文参考文献

齐有政,黄玲,张建国等.2013.层状介质上时空展源瞬变电磁响应的计算方法研究.物理学报,62(23):234201.

薛国强,李貅,底青云.2008.瞬变电磁法正反演问题研究进展.地球物理学进展,23(4):1165-1172.

殷长春,张博,刘云鹤等.2015.航空电磁勘查技术发展现状及展望.地球物理学报,58(8):2637-2653,doi:10.6038/cjg20150804.

嵇艳鞠,王远,徐江等.2013.无人飞艇长导线源时域地空电磁勘探系统及其应用.地球物理学报,56(11):3640-3650,doi:10.6038/cjg20131105.

(本文编辑 胡素芳)

A rapid 3D inversion based on TEM moment transformation

RAO Li-Ting1,2,WU Xin1,2,WU Chao1,2,ZHANG Xiao-Juan1,FANG Guang-You1

1 Key Laboratory of Electromagnetic Radiation and Sensing Technology, Chinese Academy of Sciences,Beijing 100190,China2 University of Chinese Academy of Sciences,Beijing 100039,China

A full EM solution of the 3D inversion problem is difficult to carry out on common computer due to its complex forward calculation and high demand for user resources.These restrictions make rigorous 3D inversion still impractical in the interpretation of TEM data sets.A rapid 3D inversion scheme for interpreting TEM data is presented,utilizing the concept of TEM moment.Approximate forward modeling of the 3D inversion scheme has been accomplished by adopting the first order moment transform which is the resistive limit.The modified steepest decent method is employed for inversion of the underground target response.The inherent non-uniqueness associated with the underdetermined inversion problem is balanced by including constraints in the inversion such as depth weights or conductivity weights.The fully 3D electromagnetic modeling software is employed to calculate the synthetic time-domain data to verify the proposed 3D inversion scheme.A comparison of the forward theoretical results and the moment transformed results of synthetic time-domain data shows that forward calculation gives reliable results.In order to test the inversion algorithm and examine the variability of the inversion results due to non-uniqueness,the synthetic inversion examples are explored based on different constraints.The inversion was successfully completed in dozens of seconds to recover time constant models which approximately indicated the location of the true conductive body.In conclusion,the proposed rapid 3D inversion scheme can be efficiently implemented on the normal computer which indicates a promising application prospect in real-time interpretation of TEM data.

Transient electromagnetic method (TEM)；TEM moment；Resistive limit；Rapid 3D inversion

饶丽婷，武欣，吴超等.2016.基于瞬变电磁矩变换的快速三维反演方法.地球物理学报，59(11):4338-4348,

10.6038/cjg20161133.

Rao L T,Wu X,Wu C,et al.2016.A rapid 3D inversion based on TEM moment transformation.Chinese J.Geophys.(in Chinese),59(11):4338-4348,doi:10.6038/cjg20161133.

国家重大科研装备研制项目(ZDYZ2012-1-03-01)资助.

饶丽婷，女，1989年生，博士，主要从事瞬变电磁正反演理论与方法技术研究.E-mail:raoliting11@mails.ucas.ac.cn

*通讯作者 武欣，男，1982年生，助理研究员，主要从事时间域电磁法理论与系统研发.E-mail:wu_xin18@mail.ie.ac.cn

10.6038/cjg20161133

P631

2015-11-11，2016-07-06收修定稿