地层模量分解及在流体识别中的应用
2016-11-23石玉梅曹宏孙夕平李凌高宋建勇孙虎生
石玉梅,曹宏,孙夕平,李凌高,宋建勇,孙虎生
中国石油勘探开发研究院,北京 100083
地层模量分解及在流体识别中的应用
石玉梅,曹宏,孙夕平,李凌高,宋建勇,孙虎生
中国石油勘探开发研究院,北京 100083
储层流体识别是确定油气水分布,合理布设井位,提高钻井成功率的关键之一.本文基于流体饱和孔隙介质岩石物理模型,对地震反演的地层体积模量进行分解,获得孔隙流体体积模量,并依据油、气、水(尤其是气-油、气-水)模量的显著差异进行识别.文中简要分析了Gassmann模型和Kuster-Toksöz模型的特征,详细讨论了孔隙形态和饱和度对弹性模量的影响,提出了联合Kuster-Toksöz方程和Gassmann方程的体积模量分解方法.该方法通过Kuster-Toksöz方程从测井数据中反演地层骨架固体和干骨架的弹性模量,再利用Gassmann方程对地层体积模量进行分解,既考虑了孔隙形态,又充分利用了Gassmann方程的易用性.理论模型结果表明方法是可行的.方法应用于西部地区某气田,流体识别与地层含气性预测结果与钻井基本一致,进一步证实了方法的有效性.
油气地层;岩石物理;模量分解;流体识别
1 引言
经过多年的油气勘探和开发,构造型油气藏发现的概率已越来越少,岩性地层油气藏的勘探已普遍受到人们的关注.我国陆上岩性地层油气藏多属于陆相沉积,单个油/气层薄,物性变化大,非均质性强,油、气、水关系复杂,预测难度大,因此,要提高这类油气藏预测的准确性和钻井成功率,流体识别非常必要.
由于高密度的空间采样,地震技术是进行地下流体识别的主要手段之一.地震流体识别方法可分为两大类,即属性类和参数类.属性类方法直接利用地震波的属性参数(如振幅、相位、频率等)进行流体预测,如“亮点”技术、模式识别,等.“亮点”技术是一种定性探测流体的方法,它利用的是叠后地震波的振幅属性,该方法在油气藏预测中发挥过重要作用(Robertson and Prichett,1985;Wang and Huang,1993),但在岩性差异比较大的地方,也会产生类似的“亮点”(Foster et al.,1993;Mathieu and Rice,1969;Smith and Gidlow,1987).模式识别技术以测井数据为桥梁,通过建立多地震属性与油气的映射模式进行预测(Bios,1980;Wang and Huang,1993;钱绍新,1992;刘立峰等,2014).由于采用了多属性数据的融合,模式识别技术在一定程度上缓解了单一地震属性技术的困难.参数类方法主要是基于AVO技术发展起来的,其中最具代表性的有“流体因子”法(Smith and Gidlow,1987;Smith and Sutherland,1996;Fatti et al.,1994;宁忠华等,2006)、“Lamda-Mu-Rho”法(Goodway et al.,1997;Gray et al.,1999;Ojo et al.,2005;Russell et al.,2003),等.参数类方法利用的是地层的弹性参数,与属性类方法相比,更具有物理意义.近年来,人们又发展了介于叠后和AVO技术之间的弹性阻抗技术(Connolly,1999;Gonzalezález et al.,2003;Ma and Morozov,2006;印兴耀等,2010).弹性阻抗技术利用随偏移距变化的振幅特征和局部叠加,在一定程度上克服了全偏移距数据叠加对地下地质体产生的模糊效应,同时,通过部分叠加降低了叠前振幅数据对噪声的敏感性.
地层弹性参数不但与孔隙流体有关,与岩性、孔隙度、孔隙形态等关系也很密切,地震属性类参数很大程度上还受地层间的空间接触关系影响,针对这些问题,现有方法在流体敏感性研究和预测方面取得了诸多进展,但多解性仍比较强.
Murphy等(1993)基于Biot-Gassmann模型,将地层弹性模量分解为孔隙空间模量和赋含束缚水的“干”骨架弹性模量,提出了利用纵、横波测井数据计算孔隙体积模量、获取孔隙流体模量并进行流体识别方法.Yin和Zhang(2014)利用振幅随偏移距变化及岩石物理模型,通过贝叶斯反演方法从地震数据中直接获取有效孔隙流体体积模量,并作为流体指示因子进行流体识别,降低了岩石基质尤其是孔隙度的影响.
本文利用声学全波形反演提供的地层体积模量,联合Gassmann方程和Koster-Toksöz方程进行模量分解,获得孔隙流体的体积模量,并进行流体识别.文中简要分析了Gassmann方程和Koster-Toksöz方程的特征,并通过数值计算结果讨论了不同孔隙形态情况下两者的差异,在此基础上确定了首先利用Kuster-Toksöz方程从测井数据中反演地层骨架固体和干骨架的弹性模量,再基于Gassmann方程对地层有效体积模量进行分解,获得孔隙流体体积模量并进行流体识别.文中还结合油气田开发对饱和度的要求,确定了流体识别准则.方法应用于西部某气田的实际数据,取得了比较好的预测效果,从而为后续的有效储层描述和油气藏成像提供可靠的流体分布数据.
2 流体饱和孔隙介质岩石物理模型
地震波走时、反射波波形的变化都携带有关地下岩石、流体性质的信息.从地震数据中获取这些信息岩石物理是桥梁.多年来很多学者致力于岩石物理方面的研究,先后提出了多种理论模型和经验公式(Mavko et al.,1998),Gassmann方程是其中最为常用的模型之一.随着认识的深入和油气勘探要求的提高,考虑孔隙形态的Kuster-Toksöz模型也逐渐受到了人们的重视.这里我们首先简单回顾这两个模型.
2.1 Gassmann模型
Gassmann模型的数学形式(Mavko et al.,1998):
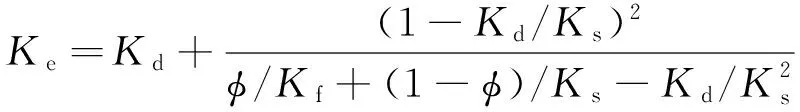
(1a)
(1b)
(1c)
其中,Kf,Km,Kd,Ke分别为孔隙流体、骨架固体、干骨架及流体饱和介质(又称有效介质)的体积模量;μe,μd分别为有效介质和干骨架的剪切模量;ρe,ρd,ρf分别为有效介质、干骨架及孔隙流体的密度;φ为孔隙度.
Gassmann模型描述了流体饱和介质弹性模量与骨架固体、干骨架、孔隙流体模量以及孔隙度的关系,适用于低频极限和孔隙流体黏度为零的情况.Gassmann方程中只涉及到总孔隙度,孔隙形态的影响通过干骨架体现(Mavko et al.,1998),但方程(1b)表示的孔隙流体存在不影响有效介质的剪切模量实际上隐含了孔隙形态为球形的假设(Toksöz et al.,1976),因此,如果不考虑剪切模量的变化,只研究流体饱和孔隙介质体积模量的变化特征,则孔隙形态效应可以通过干骨架体积模量实现.
2.2 Kuster-Toksöz模型
Kuster和Toksöz基于散射理论,导出了长波长一阶近似条件下流体饱和孔隙介质弹性模量方程,即Kuster-Toksöz方程(Kuster and Toksöz,1974;Toksöz et al.,1976).该方程通过引入孔隙纵横比(孔隙长轴与短轴之比)谱,考虑了孔隙度和孔隙形态对介质弹性模量的影响.
Kuster-Toksöz方程的形式为(Toksöz et al.,1976):

(2a)

(2b)

Kuster-Toksöz方程中,岩石的剪切模量受孔隙填充物性质影响,尤其孔隙中填充高黏度稠油.另一方面,Kuster-Toksöz方程考虑了孔隙形状,更符合实际地层.
2.3 Gassmann方程与Kuster-Toksöz方程比较
Gasmann方程与Kuster-Toksöz方程的区别主要有:(1)Kuster-Toksöz方程显示表示了有效介质弹性模量与孔隙形态的关系,而Gasmann方程的孔隙形态效应隐含在干骨架的体积模量中(Mavko et al.,1998);(2)Gasmann方程假定剪切模量为常数,不受孔隙流体的影响,Kuster-Toksöz方程中剪切模量与孔隙流体有关.Toksöz等(1976)证明了在球形孔隙情况下Kuster-Toksöz方程与Gasmann方程是等效的.下面我们通过计算,讨论非球形孔隙情况下这两方程的差异.
计算中取骨架固体体积模量Ks=38 GPa,剪切模量μs=44 GPa,孔隙度φ=15%.不同孔隙形态的干骨架弹性模量用Kuster-Toksöz方程计算获得.
图1显示了孔隙中充填CO2气体(KCO2=0.00013 GPa,ρCO2=1.87 kg·m-3)情况下分别利用Gassmann方程和Kuster-Toksöz方程计算的地层体积模量(Ke)和剪切模量(μe)随孔隙纵横比(α)变化曲线.可以看出,充填气体情况下,用Gassmann方程和Kuster-Toksöz方程计算不同纵横比孔隙地层体积模量和剪切模量结果相同.图2显示了孔隙中充填水(Kwater=2.25 GPa,ρwater=1000 kg·m-3)时的计算结果.与饱和气体情况类似,两方程计算的体积模量重合,剪切模量在小纵横比孔隙(α<0.5)时略有区别,但不很明显,可以忽略.图1和图2结果表明,在饱和气或饱和水情况下,对于不同纵横比孔隙,Gassmann方程与Kuster-Toksöz方程基本等价,这为实际数据处理时先应用Kuster-Toksöz方程从测井数据中反演骨架固体和干骨架的弹性模量,再利用Gassmann方程从地震反演获得的地层弹性模量中分解流体模量奠定了基础.

图1 饱和气时Gassmann方程和Kuster-Toksöz方程计算的弹性模量随孔隙纵横比变化Fig.1 Effective elastic moduli (calculated by Gassmann equations and Kuster-Toksöz equations,respectively) versus pore aspect radio in saturated gas
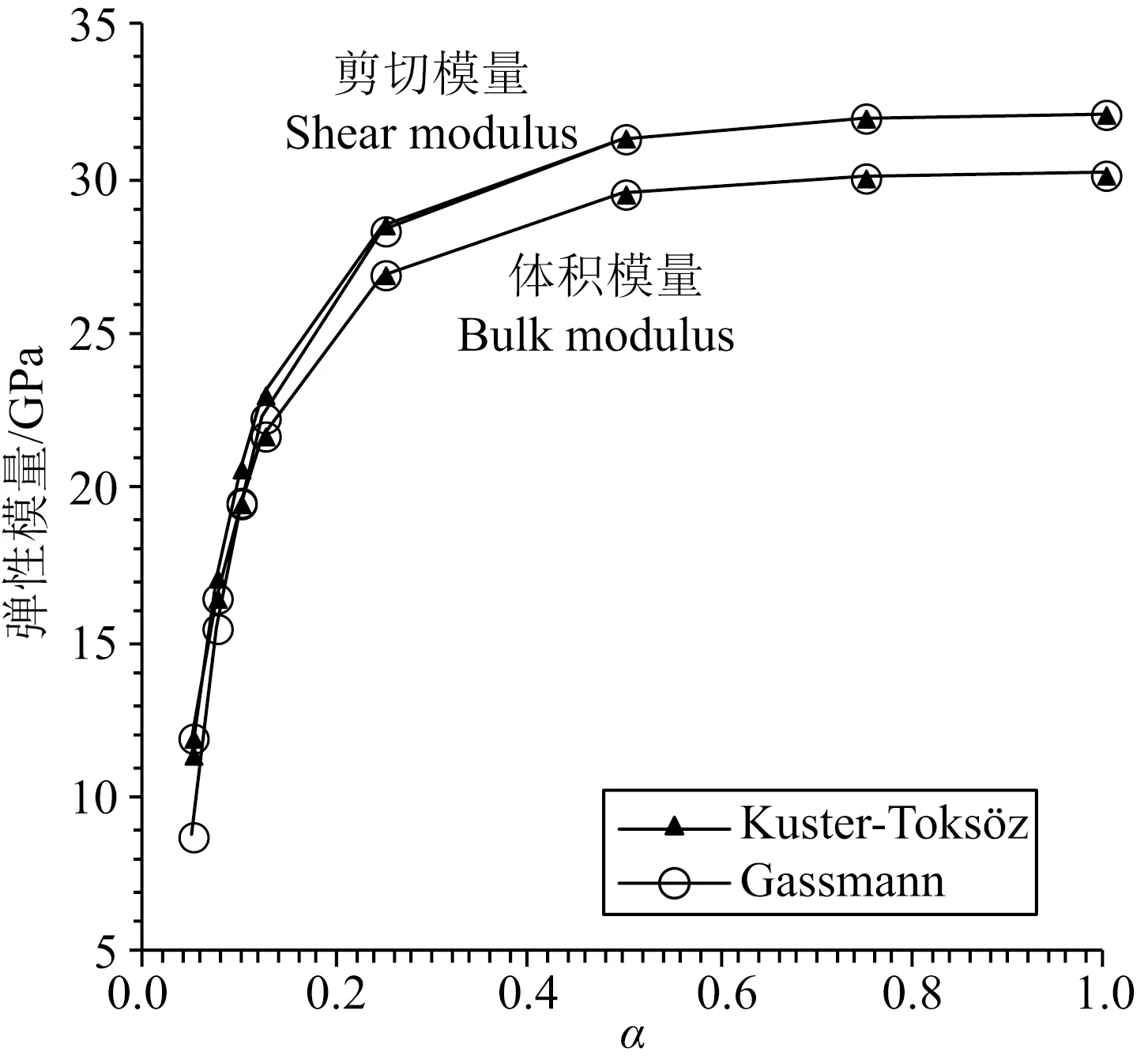
图2 饱和水时Gassmann 方程和Kuster-Toksöz方程计算的有效弹性模量随孔隙纵横比变化Fig.2 Effective elastic moduli (calculated by Gassmann equations and Kuster-Toksöz equations respectively) versus pore aspect radio in saturated water
3 模量分解及流体识别
利用弹性模量进行地下流体识别前,我们首先讨论流体的存在对地层弹性模量的影响.
3.1 流体饱和多孔介质弹性模量
考虑完全饱和水(Sw=100%)和完全饱和气(Sgas=100%)两种情况,其他参数同上.Kuster-Toksöz方程计算结果如图3a和3b所示.由图3a可以看出,无论孔隙是什么形状,饱和水的地层和饱和气的地层体积模量都有比较明显的区别,饱和水地层体积模量比饱和气地层体积模量大,且孔隙纵横比越小,这种差别越大.图3b显示,除了小孔隙纵横比时的微小差异(可以忽略)外,饱和水的地层和饱和气的地层剪切模量基本重合.因此,在识别地层中流体是气还是水时,采用体积模量更为合适.
地层孔隙中油、气和水的混合相态在实际油气藏中更为普遍.混合流体情况下地层弹性模量有何变化特征?这里我们仍然通过计算进行讨论(计算所用参数同上).
混合流体体积模量的计算采用经验公式(Brie et al.,1995):
(3)
其中,Kf为混合流体体积模量,Kliquid和Kgas分别为液体和气体体积模量,Sgas为含气饱和度,e为指数,这里取e=3.计算结果见表1.
图4显示了孔隙纵横比α=0.1时地层体积模量和剪切模量随含气饱和度的变化.图中可以看出,(1)随着含气饱和度的增加,体积模量和剪切模量都减小,且体积模量的减小幅度更大.(2)在低含气饱和度(Sgas<40%)时,体积模量随饱和度增加近似呈线性减小;当含气饱和度大于70%,体积模量的变化变得平缓.因此,在气-水情况下,(1)相对于剪切模量,体积模量对孔隙流体性质的变化更为敏感,更适合于孔隙流体识别;(2)在含气饱和度Sgas<70%情况下,可以利用体积模量很好预测孔隙中流体的含量(如含气饱和度).
3.2 体积模量分解及流体识别
地层的体积模量不但与孔隙中流体的性质及含量有关,与地层的岩性、孔隙度和孔隙形态等因素也关系密切,直接利用地层体积模量进行流体识别多解性比较强.这里,我们利用Gassmann方程从地层体积模量中分解出流体体积模量,并利用流体体积模量进行流体识别.
(1) 模量分解
重新改写Gassmann方程(1a),
(4)
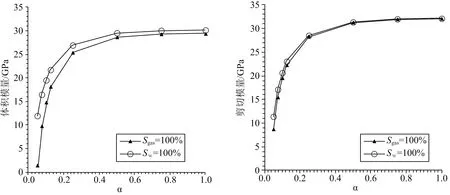
图3 饱和气和饱和水情况下有效介质体积模量(左)和剪切模量(右)随孔隙纵横比变化Fig.3 Effective bulk modulus (left) and shear modulus (right) versus pore aspect radio in saturated gas and water,respectively

图4 弹性模量随饱和度变化曲线(α=0.1) Fig.4 Elastic modulus versus gas saturation (α=0.1)
利用(4)式从地层体积模量Ke中分解出流体体积模量Kf时,需要知道地层的孔隙度φ、骨架固体体积模量Ks和干骨架体积模量Kd.φ可用石玉梅等(2010)提出的方法获得,Ks和Kd可由实验室测量获得,这里,根据Kuster-Toksöz方程(取μf=0),迭代反演地层骨架固体体积模量及剪切模量(骨架固体弹性模量反演的详细讨论将另文阐述),并在式(2a)和(2b)中取孔隙填充物体积模量和剪切模量为零,求得干骨架的弹性模量,
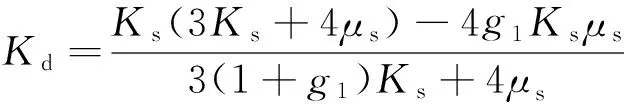
(5a)
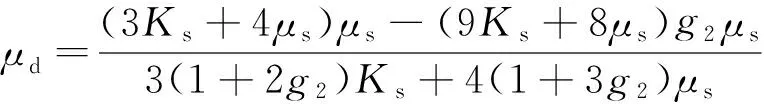
(5b)
(2) 流体识别
一般情况下,天然气的体积模量值在0.02~0.15 MPa之间,地层水的体积模量约为2.25 GPa,通常情况下(即除重油或稠油),石油的体积模量介于气和水之间,且变化范围比较大.重油或稠油的体积模量一般比水的体积模量大得多,可见,相对于油和水,用体积模量进行气和水识别要容易得多.但在油气勘探中,有时候地层孔隙中同时存在气和水(或油和水),即孔隙中的流体为混合流体,这时,我们不能简单说是气(或油)还是水.这里,我们根据生产开发确定的饱和度门槛值(即油气藏最高含水饱和度)Swc,利用式(3)计算相应的混合流体体积模量Kc,称为临界体积模量,并按下列准则进行地层含流体性识别(除重油或稠油外),即
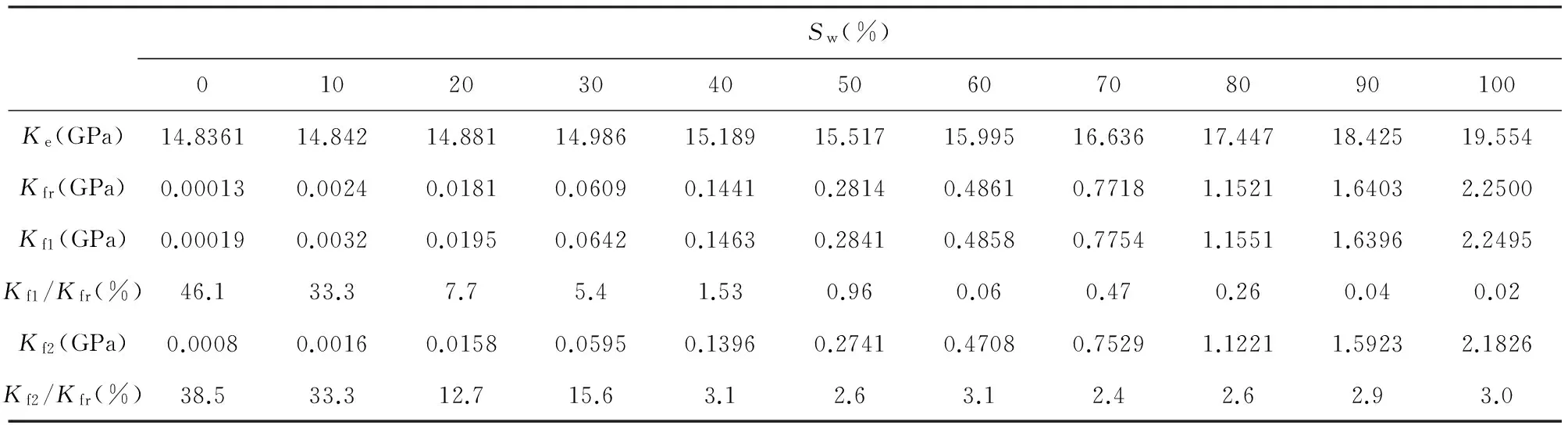
① εKg ② Kc ③ 其他:干层,即地层孔隙中不含气、油和水 (3) 流体识别的影响因素 由方程(4)和上述识别准则可以看出,影响地震油气识别的主要因素有:骨架固体体积模量,干骨架体积模量,地层有效体积模量和孔隙度. 根据方程(4),骨架固体体积模量误差dKs引起的流体体积模量预测误差dKf可用(6)式表示, (6) 可见骨架固体体积模量的影响程度除与其本身值的大小有关外,还与干骨架的体积模量、地层体积模量、孔隙度值有关.取骨架固体实际体积模量(即Ksr=38 GPa),孔隙度φ=15%,饱和度Sw=100%(实际流体体积模量Kfr=2.25 GPa),在球形孔隙情况下,相应的干骨架体积模量Kdr=29.4 GPa,饱和水后有效介质体积模量Ker=30.18 GPa.假设测量或反演获得的骨架固体体积模量Ksc=39.5 GPa,与实际值的差ΔKs=1.5 GPa,相对误差为3.95%.根据式(6)预测的流体体积模量误差ΔKf≈0.0293 GPa,相对误差约为1.3%,可见骨架固体体积模量的误差对流体体积模量估计的影响是收敛的. 同理,根据方程(4),可以获得流体体积模量预测误差与干骨架体积模量测量误差以及孔隙度测量误差的关系, (7a) (7b) 其中,dKd和dφ分别为干骨架体积模量误差和孔隙度误差. 根据(7a)和(7b)式,(1)假设干骨架体积模量测量相对误差与骨架固体相同,为3.95%,即ΔKd=1.16 GPa,则预测的流体体积模量误差ΔKf≈0.1471 GPa,相对误差约为6.5%,可见干骨架体积模量的测量误差对流体体积模量预测结果影响比较大.(2)假设测量的孔隙度值为13.5%(相对误差为10%),则预测的流体体积模量误差ΔKf≈0.0489 GPa,相对误差为2.17%;当孔隙度的相对误差与上述固体骨架体积模量相对误差相同(即为3.95%)时,引起的流体体积模量误差约为0.86%,可见与固体骨架体积模量相比,孔隙度误差对流体体积模量预测的影响更小. 地层体积模量测量误差对流体体积模量预测值影响的讨论见文献(石玉梅等,2014),这里不再赘述. 临界流体体积模量的计算方法也会影响地层含流体性质的划分.本文采用经验公式(3)计算混合流体临界体积模量.经验公式(3)计算结果介于Reuss平均和Voigt平均之间,在实际应用中,我们根据实验测得的数据或测井数据调整公式中指数值e. 4.1 模型计算 这里,我们利用上述方法对图4所示的地层体积模量进行分解,获得流体体积模量. 首先,利用Kuster-Toksöz方程反演获得的地层骨架固体体积模量和剪切模量分别为:Ksi=38.80942 GPa,μsi=44.03208 GPa(反演参数取α=0.25,Sw=65%,φ=15%,纵波速度VP=5209.5 m·s-1,横波速度VS=3478.3 m·s-1,密度ρ=2350.1 kg·m-3),与实际骨架固体模量:Ksr=38 GPa,μsr=44 GPa相比,反演结果的相对误差分别为2.13%(体积模量)和0.07%(剪切模量).再利用真实骨架固体体积模量和反演的骨架固体体积模量对图4所示的地层体积模量进行分解,获得了不同饱和度情况下孔隙流体体积模量,列于表1.由于图4对应的孔隙纵横比为0.1,因此,在进行模量分解前,我们分别根据真实的骨架固体弹性模量和反演的骨架固体弹性模量,利用方程(5a)及(5b)计算干骨架的弹性模量(α=0.1),计算结果为,① 真实骨架固体:Kdr=14.83583 GPa,μdr=19.59360 GPa;② 反演骨架固体:Kdi=14.99658 GPa,μdi=19.66223 GPa.表中,Kfr为流体真实体积模量,Kf1为用真实骨架固体模量及相应干骨架模量值分解获得的流体体积模量,Kf2为用反演的骨架固体模量及相应的干骨架模量分解获得的流体体积模量.ΔKf=|Kf-Kfr|,Kf为分解获得的流体体积模量(真实骨架固体模量时为Kf1,反演骨架固体模量时为Kf2),ΔKf1/Kfr和ΔKf2/Kfr分别为两种情况下分解得的流体体积模量的相对误差.从表中可以看出,骨架固体弹性模量反演的精度对模量分解结果有影响,反演的骨架固体弹性模量精度越高,分解的流体体积模量越接近实际.表中还可以看出,高含气情况下分解得的流体体积模量相对误差比较大,这主要是因为含气饱和度大时,孔隙中实际流体体积模量Kfr变得非常小的缘故,但对地层含气性的划分影响不是很大.总体来看,利用地层速度反演的骨架固体体积模量分解得的流体模量基本反映了流体真实的体积模量,证明了本文提出的方法是可行的. 4.2 应用研究 上述方法用于我国西部某气田模量分解和气-水识别.该气田为砂泥岩地层,储层砂体为辫状河沉积,多期河道叠置连片,纵向上厚度大,平面上大面积分布,物性差,孔隙度小,砂岩含气后与围岩波阻抗差小,致使利用纵波速度和波阻抗均不能明显区分砂岩、泥岩和气层;另一方面,该区构造平缓,属于大面积分布的非均质岩性气藏,没有明显的物性或流体界面,常规地震技术气-水识别困难.该区开发要求的含水饱和度门槛值Swc=55%,相应的临界体积模量Kc= 0.374379 GPa. 表1 有效介质体积模量、流体体积模量及误差 该区有多口钻井,我们首先利用该区岩心分析、统计获得的孔隙纵横比谱(列于表2)和测井数据反演井位置处地层骨架固体体积模量和剪切模量,再利用内插和外推方法获得该区地层骨架固体体积模量和剪切模量.地层干骨架的体积模量利用反演的骨架固体弹性模量和孔隙度数据(石玉梅等,2014)计算获得. 该区地震数据为高密度采集:道间距10 m,炮间距40 m,最大偏移距4000 m,记录长度5 s,1 ms采样,双边接收.我们对采集的数据进行了静校正、地表一致性振幅补偿、叠前去噪等预处理后,利用声学全波形反演,获得了地层体积模量(石玉梅等,2014),如图5所示.地层体积模量剖面上呈现三个明显的高值条带.地层体积模量是岩性、孔隙和孔隙流体等多因素的综合反映,这三个高值条带区域为砂岩层,可能含气.图6显示了模量分解获得的流体体积模量剖面.图中绿-黄-兰色表示模量值逐渐增大,黄色为气区,兰色为水饱和区(或含水饱和度大),绿色为无气区.可以看出J1d上覆地层体积模量大的条带,其上部基本为水层,下部为无气地层;在井W2附近,J1z以上以及T3X4—T3X5之间相对低的地层体积模量带含水饱和度比较高,T3X6—J1z之间的地层以及井W1附近的T3X4—T3X5之间的地层主要为气体分布,两井之间的各地层也有气体分布,这与该区的成藏特征一致,井孔处的天然气分布预测结果与钻井基本吻合.预测结果为后续的气藏成像提供了可靠的流体分布数据. 表2 孔隙纵横比谱 图5 声学全波形反演的地层体积模量剖面Fig.5 Section of bulk modulus using acoustic full wave inversion 图6 流体体积模量剖面Fig.6 Section of fluid bulk modulus Gassmann方程由于其易用性,是目前研究流体饱和多孔介质弹性特征时普遍采用的一种岩石物理模型,Kuster-Toksöz方程充分考虑了孔隙的形态对地层弹性模量的影响,更符合实际地层.联合Gassmann方程和Kuster-Toksöz方程进行体积模量分解,一方面,在实验室测量数据缺乏地区,通过测井数据可以获得地层骨架固体及干骨架的弹性模量,为流体模量分解提供数据,另一方面,也在一定程度上提高了流体体积模量预测的精度,且易于实现. 孔隙流体的体积模量与流体性质、各组分的比例有关,同时受温度、压力影响比较大,但对于一个确定的研究区,后两因素基本确定,因此,流体体积模量主要取决于前两因素,直接利用流体体积模量进行流体预测可显著降低结果的多解性.另一方面,在已知研究区流体体积模量与饱和度关系情况下,根据流体体积模量可以预测油气饱和度,从而为精细油藏描述提供流体分布模型. 利用流体体积模量识别流体的结果反映的是地下流体分布状况,油气分布区域是否形成有效的油气藏还与地层的孔隙度密切相关,如孔隙度非常小,通常认为是“干层”或“微气”层,只有孔隙度和饱和度都达到一定值,才能形成有效的油气藏,因此,气的分布区域可能比较大,但有效的油气藏分布区域却可能很小,如我国中、西部的苏里格气田和广安气田,气体大面积分布,但有效气藏只限于其中的“甜点”区域. Bios P.1980.Autoregressive pattern recognition applied to the delimitation of oil and gas reservoirs.Geophysical Prospecting,28(4):572-591. Brie A,Pampuri F,Marsala A F,et al.1995.Shear sonic interpretation in gas-bearing sands.∥SPE Annual Technical Conference and Exhibition.Dallas,Texas:SPE:701-710. Connolly P.1999.Elastic impedance.The Leading Edge,18(4):438-452,doi:10.1190/1.1438307. Fatti J L,Smith G C,Vail P J,et al.1994.Detection of gas in sandstone reservoirs using AVO analysis:A 3-D seismic case history using the geostack technique.Geophysics,59(9):1362-1376,doi:10.1190/1.1443695. Foster D J,Smith S W,Dey-Sarkar D,et al.1993.A closer look at hydrocarbon indicators.∥63thSEG Expanded Abstracts.SEG:731-734. Gonzalezález E F,Mukerji T,Mavko G,et al.2003.Near and far offset P-to-S elastic impedance for discriminating fizz water from commercial gas.The Leading Edge,22(10):1012-1015,doi:10.1190/1.1623642. Goodway B,Chen T W,Downton J.1997.Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters;“λρ”,“μρ”&“λ/μ” fluid stack,from P and S inversions.∥67thSEG Expanded Abstracts.SEG:183-186. Gray D,Goodway B,Chen T W.1999.Bridging the gap:using AVO to detect changes in fundamental elastic constants.∥69thSEG Expanded Abstracts.SEG:852-855. Kuster G T,Toksöz M N.1974.Velocity and attenuation of seismic waves in two-phase media:Part 1.Theoretical formulations.Geophysics,39(5):587-606,doi:10.1190/1.1440450. Liu L F,Sun Z D,Han J F,et al.2014.A carbonate fluid identification method based on quantum particle swarm fuzzy neural network.Chinese J.Geophys.(in Chinese),57(3):991-1000,doi:10.6038/cjg20140328. Ma J F,Morozov I B.2006.A fluid detection study from Zoeppritz Elastic Impedance.∥76thSEG Expanded Abstracts.SEG:284-288. Mathieu P G,Rice G W.1969.Multivariate analysis used in the detection of stratigraphic anomalies from seismic data.Geophysics,34(4):507-515,doi:10.1190/1.1440027. Mavko G,Mukerji T,Dvorkin J.1998.The Rock Physics Handbook:Tools for Seismic Analysis of Porous Media.Cambridge:Cambridge University Press. Murphy W,Reischer A,Hsu K.1993.Modulus decomposition of compressional and shear velocities in sand bodies.Geophysics,58(2):227-239,doi:10.1190/1.1443408. Ning Z H,He Z H,Huang D J.2006.High sensitive fluid identification based on seismic data.Geophysical Prospecting for Petroleum (in Chinese),45(3):239-241. Ojo C,Licalsi P,Gemelli S,et al.2005.Lambda-Rho processing—A tool to reveal full hydrocarbon potentials:Onshore Nigeria processing,interpretation and drilling case history.∥75thSEG Expanded Abstracts.SEG:1315-1318. Qian S X.1992.Application of pattern recognition technique to lateral prediction of hydrocarbon reservoir.Chinese J.Geophys.(Acta Geophysica Sinica) (in Chinese),35(5):630-636. Robertson J D,Prichett W C.1985.Direct hydrocarbon detection using comparative P-wave and S-wave seismic section.Geophysics,50(3):383-393,doi:10.1190/1.1441918. Russell B H,Hedlinz K,Hilterman F J,et al.2003.Fluid-property discrimination with AVO:A Biot-Gassmann perspective.Geophysics,68(1):29-39,doi:10.1190/1.1543192. Shi Y M,Yao F C,Sun H S,et al.2010.Density inversion and porosity estimation.Chinese J.Geophys.(in Chinese),53(1):197-204,doi:10.3969/j.issn.0001-5733.2010.01.022. Shi Y M,Zhang Y,Yao F C,et al.2014.Methodology of seismic imaging for hydrocarbon reservoirs based on acoustic full waveform inversion.Chinese J.Geophys.(in Chinese),57(2):607-617,doi:10.6038/cjg20140224. Smith G C,Gidlow P M.1987.Weighted stacking for rock property estimation and detection of gas.Geophysical Prospecting,35(9):993-1014. Smith G C,Sutherland R A.1996.The fluid factor as an AVO indicator.Geophysics,61(5):1425-1428,doi:10.1190/1.1444067. Toksöz M N,Cheng C H,Timur A.1976.Velocities of seismic waves in porous rocks.Geophysics,41(4):621-645,doi:10.1190/1.1440639. Wang J L,Huang K Y.1993.Neural networks for robust recognition of seismic reflection patterns.∥63thSEG Expanded Abstracts.SEG:246-249. Yin X Y,Zhang S X.2014.Bayesian inversion for effective pore-fluid bulk modulus based on fluid-matrix decoupled amplitude variation with offset approximation.Geophysics,79(5):R221-R232,doi:10.1190/GEO2013-0372.1. Yin X Y,Zhang S X,Zhang F C,et al.2010.Utilizing Russell Approximation—based elastic wave impedance inversion to conduct reservoir description and fluid identification.Oil Geophysical Prospecting (in Chinese),45(3):373-380. 附中文参考文献 刘立峰,孙赞东,韩剑发等.2014.量子粒子群模糊神经网络碳酸盐岩流体识别方法研究.地球物理学报,57(3):991-1000,doi:10.6038/cjg20140328. 宁忠华,贺振华,黄德济.2006.基于地震资料的高灵敏度流体识别因子.石油物探,5(3):239-241. 钱绍新.1992.应用模式识别方法预测油气储集层.地球物理学报,35(5):630-636. 石玉梅,姚逢昌,孙虎生等.2010.地震密度反演及地层孔隙度估计.地球物理学报,53(1):197-204,doi:10.3969/j.issn.0001-5733.2010.01.022.石玉梅,张研,姚逢昌等.2014.基于声学全波形反演的油气藏地震成像方法.地球物理学报,57(2):607-617,doi:10.6038/cjg20140224. 印兴耀,张世鑫,张繁昌等.2010.利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别.石油地球物理勘探,45(3):373-380. (本文编辑 何燕) Formation modulus decomposition and its application to discrimination of pore fluid SHI Yu-Mei,CAO Hong,SUN Xi-Ping,LI Ling-Gao,SONG Jian-Yong,SUN Hu-Sheng Research Institute of Exploration and Development,PetroChina,Beijing 100083,China Fluid discrimination is important for predicting the distribution of oil/gas/water and the arrangement of wells.It is also one of the keys to improve the success ratio of drilling.In this paper,we briefly analyze the Gassmann equation and Kuster-Toksöz equation which are used to describe the elastic characteristics of the fluid saturated porous medium and discuss the formation elastic characteristics for various pore morphology and saturation.A method based on the both equations is presented to decompose the formation bulk modulus which is derived from seismic inversion,and then to identify the pore fluid according to the differential bulk modulus between oil,gas and water.This method has been tested successfully by a theoretical model and field data from western China.The drilling results demonstrate that this method is effective in fluid discrimination and prediction of gas reservoirs. Hydrocarbon formation;Rock physics;Modulus decomposition;Fluid identification 石玉梅,曹宏,孙夕平等.2016.地层模量分解及在流体识别中的应用.地球物理学报,59(11):4278-4286, 10.6038/cjg20161128. Shi Y M,Cao H,Sun X P,et al.2016.Formation modulus decomposition and its application to discrimination of pore fluid.Chinese J.Geophys.(in Chinese),59(11):4278-4286,doi:10.6038/cjg20161128. 国家重大科技专项(2016ZX05001)和国家自然科学基金(41504110)资助. 石玉梅,女,1964年生,1989年毕业于成都地质学院应用地球物理专业,1992年获成都地质学院应用地球物理专业硕士学位,2001年获中国矿业大学地球探测与信息技术博士学位.主要从事波动方程正反演、时移地震、多分量地震理论和方法研究.E-mail:symei@petrochina.com.cn 10.6038/cjg20161128 P631 2015-04-24,2016-09-28收修定稿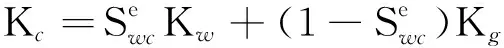

4 模型和应用研究
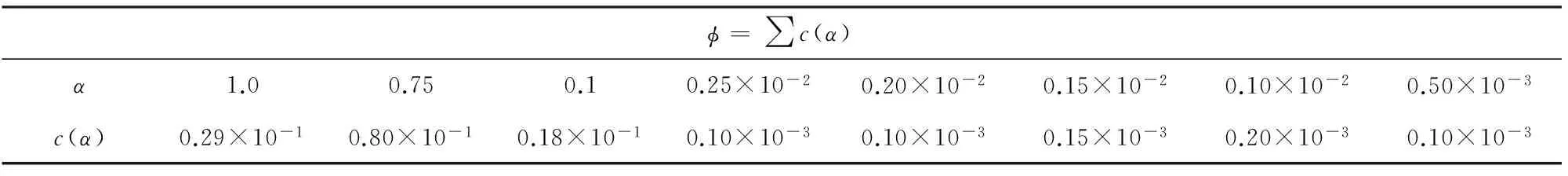


5 结论
