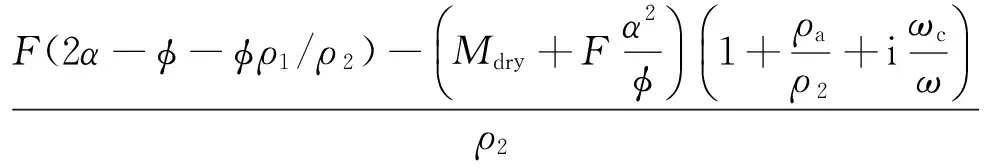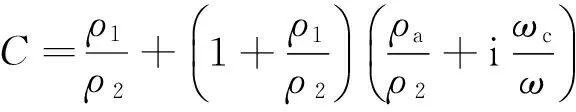基于自适应杂交遗传算法的CO2地质封存的储层参数反演研究
2016-11-23郝艳军杨顶辉程远锋
郝艳军,杨顶辉*,程远锋
1 清华大学数学科学系,北京 1000842 中国石化集团胜利油田分公司物探研究院,山东东营 257001
基于自适应杂交遗传算法的CO2地质封存的储层参数反演研究
郝艳军1,杨顶辉1*,程远锋2
1 清华大学数学科学系,北京 1000842 中国石化集团胜利油田分公司物探研究院,山东东营 257001
二氧化碳地质封存是减少温室气体排放和减缓温室效应的重要手段.二氧化碳封存的一个重要组成部分是地震监测,即用地震的方法监测封存后的二氧化碳的分布变化.为了实现这个目标,需要建立储层参数与地震性质之间的关系(岩石物理模型)和从地震监测数据中反演获得储层流体的饱和度等参数.首先,本文以Biot理论为基础,结合多相流模型研究了多个物理参数(孔隙度、二氧化碳饱和度、温度和压力等)对同时含有二氧化碳和水的孔隙介质的波速和衰减等属性的影响.结果表明:孔隙度和二氧化碳饱和度对岩石的频散和衰减属性影响强烈,而温度和压力通过孔隙流体性质对岩石的波速产生影响.然后,本文基于含多相流的Biot理论,应用抗干扰能力强、且具有更好的局部搜索能力和抗早熟能力的自适应杂交遗传算法对实际数据进行了反演研究.对岩心实验数据的反演研究表明了算法的有效性,而且表明含多相流的Biot理论能够很好地解释水和二氧化碳饱和岩石的波速特征.最后,我们将自适应杂交遗传算法应用于实际封存项目的地震监测数据,获得了封存后不同时期的二氧化碳饱和度,达到了用地震方法监测二氧化碳分布的目的.
二氧化碳地质封存;Biot理论;多相流;遗传算法;储层参数反演
1 引言
从工业革命开始,人类对化石能源的大规模利用使大量的二氧化碳被排入大气层,由此导致的碳循环不平衡引起了严重的温室效应.二氧化碳捕获和封存(CCS)是减少二氧化碳排放和减缓温室效应的有效途径(Metz et al.,2005;Bachu,2008;郝艳军和杨顶辉,2012).经过二十多年的发展,众多的试验性二氧化碳封存项目证明CCS可以大幅减少从煤电厂和水泥厂等工业设施排放的二氧化碳,从而减缓温室效应.可行的封存方式主要有三种:地质封存,海洋封存和矿化封存,其中地质封存具有最大的封存潜力,并且实施起来也最容易.矿化封存的封存量较少,而海洋封存会使海水酸化,对环境以及生态造成未知的影响,因此二者在实用性上都远不如地质封存(Metz et al.,2005).完整的地质封存包括三方面:从碳源(煤电厂、水泥厂等)将二氧化碳从废气中分离并运输到封存地点,将二氧化碳持续注入地层中,以及注入之后对二氧化碳的分布进行监测以保证安全性.适合于封存二氧化碳的地质构造包括深部咸水层、枯竭油气田和不可开采的煤层,其中深部咸水层具有最大的潜力,据估计可以封存多达104Gt二氧化碳(Metz et al.,2005).为了监测注入地下的二氧化碳的分布变化,首先需要对封存之后地层中的所有物理和化学过程有一个全面的认识.注入二氧化碳后,储层流体(水、CO2、油、气等等)形成复杂的多相流,在重力以及各种流相的压力差驱动下流动,较轻的CO2会上浮并受到盖层的阻挡而留在储层中.二氧化碳溶解于水形成碳酸,进而与储层岩石发生反应形成新的矿物,在一个相当长的时期内改变储层的岩性、孔隙度和渗透率等属性.由于二氧化碳的物理性质对于温度和压力十分敏感,注入二氧化碳导致的温度和压力变化会使整个物理和化学过程变得更加复杂.针对影响这些复杂物理和化学过程的重要因素(诸如相对渗透率、毛管压力、化学反应种类和速率、储层温度和压力等)的模拟研究已有很多(Rutqvist et al.,2001;Pruess,2005;Doughty,2007;Gaus et al.,2008;Birkholzer et al.,2009),这些工作揭示了二氧化碳地质封存的物理和化学过程的特殊性,为储层地震监测打下了基础.
在二氧化碳封存过程中和封存后,需要长时期的监测以确保封存的安全性,避免泄露对周围人类和环境的危害,因此监测方法至关重要.经过长时期的实践,地震方法已被证明是最有效且便宜的对二氧化碳分布进行监测的手段,且已经在很多封存项目中被成功运用(Michael et al.,2010).在美国德克萨斯州Frio构造进行的实验性CO2封存项目中,时移VSP方法和井间地震层析成像方法对CO2的监测结果与数值模拟所预测的结果相符,显示出大量CO2因相对渗透率降低而被封存在储层中(Hovorka et al.,2006).挪威Sleipner的CO2封存项目是4D地震成功实施的典范,由于CO2被咸水层中的薄泥岩层所阻挡,不同时期的地震剖面上显示出非常明显的反射振幅增强以及时间下推效应(Chadwick et al.,2009).In Salah气田的CO2封存项目综合使用了地震方法、InSAR以及地球化学方法等来监测封存后储层的变化,而4D地震方法为项目提供了高质量的储层剖面图像(Mathieson et al.,2011).Zhang等(2013)应用全波形反演的方法对德国Ketzin封存项目的时移地震数据进行了反演研究,反演的CO2分布结果与数值模拟结果相吻合.Bergmann等(2016)总结了在德国Ketzin地区的CO2实验性封存项目的地球物理监测结果.在这个欧洲首个陆上CO2封存项目中,研究者综合使用了各种地球物理方法来监测地下CO2的运移,例如4D地震调查、VSP方法、井间调查、MSP方法以及电阻率层析成像等方法.其中,4D地震技术被证明是最为有效的方法,为观测井位置选取以及封存量估计提供了重要依据(Bergmann et al.,2016).
二氧化碳注入之后,储层的各种属性,如流体组分、饱和度、压力、温度、孔隙度、渗透率、岩石骨架和岩性等,都会经历一定程度的变化.这些变化都会反映在储层的地震属性上,所以我们需要发展能够描述这些地质属性变化对地震属性影响的理论,即岩石物理模型.岩石物理模型是连接储层中流体组分和饱和度等属性与地震属性的桥梁,也是地震监测成功的关键.适合于封存二氧化碳的储层属于典型的含流体孔隙介质,针对这种双相(流-固耦合)介质中的波传播理论研究已有半个多世纪的历史.在大量的研究工作中,Gassmann(1951)和Biot(1956a,b)的工作,即被后人称为Biot-Gassmann理论的工作,奠定了含流体多孔隙双相介质理论的基础.Biot通过引入地震波导致的流体宏观流动(Biot流),建立了双相介质中地震波传播的Biot(1956a,b)理论,并预测了慢P波的存在.模型的有效性需要实验的验证,近几年涌现出了很多测量含二氧化碳的岩石储层中的波速和衰减实验研究(Lei and Xue,2009;Siggins et al.,2010;Shi et al.,2011;Lebedev et al.,2013;Nakagawa et al.,2013;Mikhaltsevitch et al.,2014;Zhang et al.,2015).目前多数研究更偏向于测量超声波段(0.2~1 MHz)的数据,而低频的波速和衰减测量则存在技术上的困难(Zhao et al.,2013).直接使用超声波段测量的数据对地震数据进行校正是有问题的,因为波速存在频散的现象.就我们所知,Mikhaltsevitch等(2014)针对含有二氧化碳和水的砂岩储层进行的低频(0.1~100 Hz)频散和品质因子的测量是我们目前已知唯一的地震频段实验.
地震监测的目的是获得封存之后的随时间变化的二氧化碳分布(MacBeth et al.,2006;Azuma et al.,2011;Queißer and Singh,2013),而储层参数反演可以达到这个目的.岩石物理模型提供了储层参数与地震数据之间的关系,因此应用储层参数反演方法可以从地震数据中反演得到储层参数,尤其是CO2饱和度分布.根据选取的岩石物理模型的不同,储层参数反演可能是有很强非线性的计算过程,一般的局部搜索算法例如共轭梯度法、最速下降法和单纯形法等可能很难得到全局最优解.在这种情况下,随机算法可以发挥更大的作用.遗传算法作为一种随机算法已经被用到很多反演问题中,在地球物理领域也有广泛的应用(杨磊等,2014;Fang and Yang,2015).但是诸如遗传算法等随机算法也面临着容易早熟和易陷入局部最优解等问题.为了解决这些问题,Fang 和 Yang(2015)提出了一种自适应杂交遗传算法,通过引入罚函数来自适应地调整个体的适应值和交叉概率,然后利用模拟退火的方法对接受概率进行评价.通过这些综合的改进,有效提高了遗传算法的局部搜索能力和预防早熟的能力,从而在进行反演的时候可以有效提高反演成功率和计算效率.
本文以Biot理论为基础,结合多相流模型来分析CO2和水饱和岩石中的多个物理参数对波速和衰减等属性的影响,并应用杂交遗传算法对Mikhaltsevitch等(2014)的岩石物理数据进行参数反演研究,验证了模型的有效性.最后,应用杂交遗传算法对实际的二氧化碳封存项目的储层地震监测数据(Queißer and Singh,2013)进行储层参数反演,获得了不同时期的二氧化碳饱和度分布,实现了地震监测的目的.
2 含多相流的Biot理论及其分析
在本节中,我们将详细阐述含多相流的Biot理论,并分析多个物理参数:CO2饱和度、孔隙度、温度、孔隙压力和有效压力对于快P波和S波的速度和衰减的影响.
2.1 含多相流的Biot理论
部分应力形式的三维Biot方程为(Biot,1956a,b;杨磊,2014)

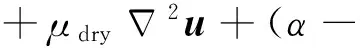
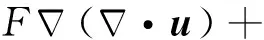
(1)
其中u和U分别是固体和流体的位移向量,λdry=Kdry-2μdry/3和μdry是岩石骨架的拉梅系数,Kdry是岩石骨架的体积模量,φ和k分别是岩石的孔隙度和渗透率,η是流体的黏度.α=1-Kdry/K0称为Biot系数,其中K0是岩石矿物的体积模量.F=[1/Kf+1/(φ Q)]-1,其中Kf是流体的体积模量,参数Q的表达式为[(1-α)/Kdry-(1-α+φ)/K0]-1.密度项可以表达为ρ11=(1-φ)ρs+ρa,ρ22=φ ρf+ρa,ρ12=-ρa,其中ρs和ρf分别是岩石矿物和流体的密度,ρa是固流耦合密度.将谐波解代入Biot方程中,通过分析可以得到两种P波和S波的频散和衰减表达式,详细表达式见附录.
由于岩石中同时含有两种流体(水和二氧化碳),为了使用Biot理论计算波传播性质需要将两种流体等效为一种流体,将两组流体参数整合为一组流体参数.混和流体的等效流体密度等于两种流体相对于饱和度的加权平均,即ρf=Slρl+Sgρg.其中S代表饱和度,下脚标l和g分别代表液相和气相,在我们所考虑的问题中水是液相,二氧化碳是气相(虽然在深部咸水层中二氧化碳一般处于超临界流体状态,但是为了简便仍用气相来称呼).对于混合流体的黏度,我们采用Carcione等(2006)中的关系式来计算:η=ηg(ηl/ηg)Sl,其中ηl和ηg分别是液相和气相的黏度.混合流体的体积模量在计算波度和衰减时是一个很关键的参数.通常来讲,两种流体混合之后的等效模量处于Ruess平均和Voigt平均之间(Mavko et al.,2003),公式为
(2)
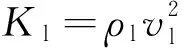
(3)
由Brie公式计算的模量介于Ruess平均和Voigt平均之间.研究表明在计算波速时使用Brie公式计算的混合流体模量能够得到和实际数据更匹配的结果(Lumley,2010),但是也要注意其中的参数e的选择.在实际中,岩石的弹性性质是受到多方面因素控制的,例如岩石的压实、沉积历史、黏土含量、岩性和孔隙形状,孔隙流体的黏度、密度、浸润性、流体种类和比例,以及环境的温度和压力等等.因此Biot理论的适用性要取决于储层岩石本身的物性,在应用时需要根据储层条件谨慎选择合适的岩石物理理论.
2.2 CO2饱和度对波频散和衰减的影响
为了分析CO2饱和度对波频散和衰减的影响,我们根据Carcione等(2006)中二氧化碳封存的地震模拟的一个算例选取如下一组参数:岩石干骨架体积模量为Kdry=1.37 GPa,剪切模量为μdry=0.85 GPa;岩石矿物的模量为K0=40 GPa,密度为ρs=2600 kg·m-3.孔隙度为φ=0.3,渗透率为k=10-12m2.水的密度为ρl=995.72 kg·m-3,声速为vl=1549.4 m·s-1,黏度为ηl=6.3019×10-4Pa·s;CO2的密度为ρg=665.37 kg·m-3,声速为vg=278.0 m·s-1,黏度为ηg=5.1743×10-5Pa·s.固流耦合密度是ρa=200 kg·m-3.在公式(3)中,选取指数e=2.0.岩石骨架的这组参数对应于高孔隙度高渗透率的未固结砂岩.
图1和图2给出了当CO2的饱和度分别为0.1,0.3,0.65和0.8时,快P波和S波的频散和衰减曲线.其中,图1a和1b分别是当饱和度取4个不同值时快P波波速和逆品质因子随频率变化的曲线.从图1a中可见,在某一固定频率下,快P波速度随着CO2饱和度的增加而减小,这说明快P波速度对岩石整体的可压缩性较为敏感,而当CO2饱和度增加时,岩石整体的可压缩性减小;当CO2饱和度为定值时,随着频率的增加,快P波的速度略有增加.4条曲线对应的最大频散分别为(按CO2饱和度从小到大排列):28.9 m·s-1,12.4 m·s-1,2.0 m·s-1,12.0 m·s-1.从图1b中可见,逆品质因子在较高频率时(>104Hz)随着CO2的饱和度增加而减小,但是频率较低时没有表现出类似的关系.逆品质因子的峰值所对应的频率随着CO2饱和度的增加而降低,这可以通过对附录A中的临界频率的表达式进行分析而得知;逆品质因子的峰值随着CO2饱和度的增加先减小,后增加.对比图1a中4条曲线的最大频散值可以发现,频散越大,逆品质因子的峰值越高.

图1 当CO2饱和度取不同值时快P波的(a)频散和(b)衰减曲线Fig.1 (a)Dispersion and(b)attenuation curves of fast P-waves at different CO2 saturation values
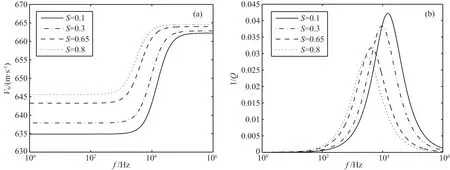
图2 当CO2饱和度取不同值时S波的(a)频散和(b)衰减曲线Fig.2 (a)Dispersion and(b)attenuation curves of S-waves at different CO2 saturation values
图2a和2b分别是当CO2饱和度取不同值时的S波波速和逆品质因子随频率变化的曲线.从图2a可见,在某一固定频率下,S波速度随着CO2饱和度的增加而增加,说明S波速度对岩石整体的密度更加敏感,对于CO2饱和度的增加而引起的岩石可压缩性变化不敏感;当CO2饱和度为定值时,S波的速度随着频率的增加.4条曲线对应的最大频散分别为(按CO2饱和度从小到大排列):27.4 m·s-1,24.9 m·s-1,20.7 m·s-1,19.0 m·s-1.从图2b可见,较高频率下(>104Hz),逆品质因子随着CO2的饱和度增加而减小,在较低频率时则呈现相反的趋势.逆品质因子的峰值所对应的频率随着CO2饱和度的增加而降低,这和快P波的表现相同;逆品质因子的最大值随着CO2饱和度的增加而减小.与图2a中4条曲线的最大频散值对比可以发现,频散越大,逆品质因子的峰值越高.
2.3 饱和度和孔隙度对波速的影响
现在我们来分析饱和度和孔隙度两个参数对快P波和S波速度的影响.频率固定为50Hz,其余参数和2.2节中相同.图3a和3b分别展示了当CO2饱和度为0.1、0.3、0.5、0.7和0.9时快P波和S波的波速随孔隙度的变化.从图中可见,当孔隙度固定时,随着CO2饱和度的增加,快P波的速度减小,而S波的速度增加,这与图1a和图2a一致.当CO2饱和度小于等于0.7时,快P波速度随着孔隙度的增加而减小;但是当CO2饱和度为0.9时,快P波速度随着孔隙度的增加先减小,后增加.对于S波并没有这样的表现,即若CO2饱和度固定,S波速度随着孔隙度的增加而增加.综合图1、2和3可知,P波和S波波速受到岩石可压缩性和密度的共同作用,而孔隙度和流体饱和度的变化对于岩石可压缩性和密度的影响是互相耦合的,所以二者对波速的影响是比较复杂的.
2.4 温度和孔隙压力对波速的影响
由于二氧化碳的各种物理参数:密度、声速和黏度,对温度和压力比较敏感,所以含有CO2的岩石的波速受温度和压力的影响比较大.为了模拟温度和孔隙压力对快P波和S波速度的影响,需要获得水和CO2在不同温度和压力下的各种物理参数值.一般来讲,需要通过状态方程来计算某一种流体的物理参数,不过这是一个很耗时和复杂的过程,所以我们使用NIST Chemistry WebBook的数据库(Linstrom and Mallard,2001)来获得不同温度和压力下水和CO2的物理参数.设定二氧化碳的饱和度为0.5,频率为50 Hz,除了水和CO2的物理参数通过数据库获得外,其他参数和2.2节中相同.我们分别计算了温度T为303.15 K,308.15 K,313.15 K,318.15 K,323.15 K,孔隙压力从7 MPa增加到15 MPa时的快P波速度和S波速度.图4a和4b分别给出了快P波速度和S波速度.图4a显示,在较低压力下快P波速度随温度的增加而增加;在较高压力下,快P波速度随温度的增加而减小.对于同一温度,快P波速度随着孔隙压力的增加先减小,后增加.对于S波,速度随温度和压力变化的规律比较清晰.对于同一压力,S波速度随着温度的增加而增加;对于同一温度,速度随着压力的增加而减小.从图4a和4b中可见当T=303.15 K,压力在7至8 MPa之间时,波速变化最为剧烈,而且显示出随压力的非单调性变化.这是因为CO2的物性在其临界点(304.13 K,7.38 MPa)附近变化很大,密度等物理量随压力和温度是呈现非单调性变化的,而在其他区域变化则较为平缓(Linstrom and Mallard,2001).从P波和S波不同的表现来看,P波速度对于CO2的声速和密度变化都比较敏感,所以在CO2的临界点处会发生非单调的变化;S波则只对CO2的密度变化比较敏感,所以其变化趋势则比较单一.

图3 不同CO2饱和度下(a)快P波波速和(b)S波波速随孔隙度的变化Fig.3 (a)Fast P-wave and(b)S-wave velocity as functions of porosity at CO2 saturations
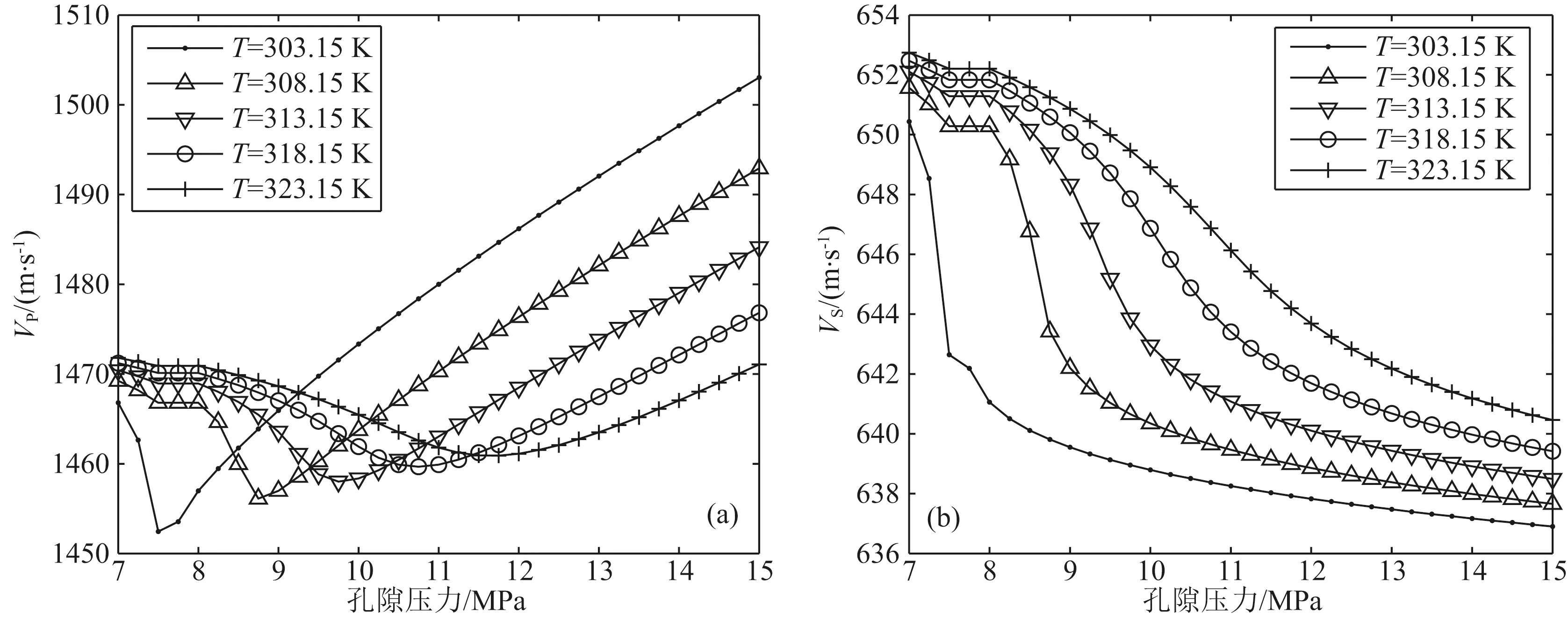
图4 不同温度下(a)快P波波速和(b)S波波速随孔隙压力的变化Fig.4 (a)Fast P-wave velocity and(b)S-wave velocity as functions of pore pressure at different temperatures
3 应用自适应杂交遗传算法对实测数据进行反演
遗传算法的基本原理是将优化问题的解编码转化为遗传空间的基因,初始化生成一定数量的种群,计算它们的适应值,然后通过选择算子、交叉算子和变异算子生成新一代的个体,如此迭代直到最优解(适应值最大).传统的二进制编码的遗传算法的解精度不高、存储量大、计算效率低,容易产生“海明悬崖”问题,而实数编码的遗传算法能够解决这些问题.此外,传统遗传算法还具有易早熟、容易陷入局部最优解等问题.为此,Fang 和 Yang(2015)提出了一种自适应的杂交遗传算法,引入罚函数调整个体的适应值和交叉概率,以保护种群多样性和避免早熟现象,同时利用模拟退火的方法对接受概率进行评价.对合成数据和实测数据的反演研究表明,这种自适应杂交遗传算法具有更好的局部搜索能力,更高的精度,更快的收敛率和计算速度.我们将应用此算法对实测数据进行反演研究.
3.1 对岩心数据的反演
我们选取Mikhaltsevitch等(2014)的数据进行反演研究.针对澳大利亚Donnybrook砂岩样本,Mikhaltsevitch等(2014)测量了超声频段的干岩石、水饱和岩石以及水和CO2混合饱和岩石的波速随有效压力变化的数据,以及三种岩石的低频(0.1~100 Hz)下的波频散和衰减的数据.
首先考察岩石干骨架的波速随有效压力的变化关系.有效压力是围压和孔隙压力的差值,Eberhart-Phillips等(1989)指出,砂岩的波速是有效压力的指数函数.相应地,岩石的体积模量和剪切模量也是有效压力的指数函数.因此我们采用如下的指数函数关系,公式为
(5)
用P波和S波速度随有效压力变化的数据来分别反演其中的参数:a1,b1,c1,a2,b2,c2.定义目标函数为
(6)

一般情况下标准的遗传算法求解的是一个极大值问题,因此通过下面的公式将(6)式转化为极大值函数(杨磊等,2014),求解相应的优化问题,公式为
(7)
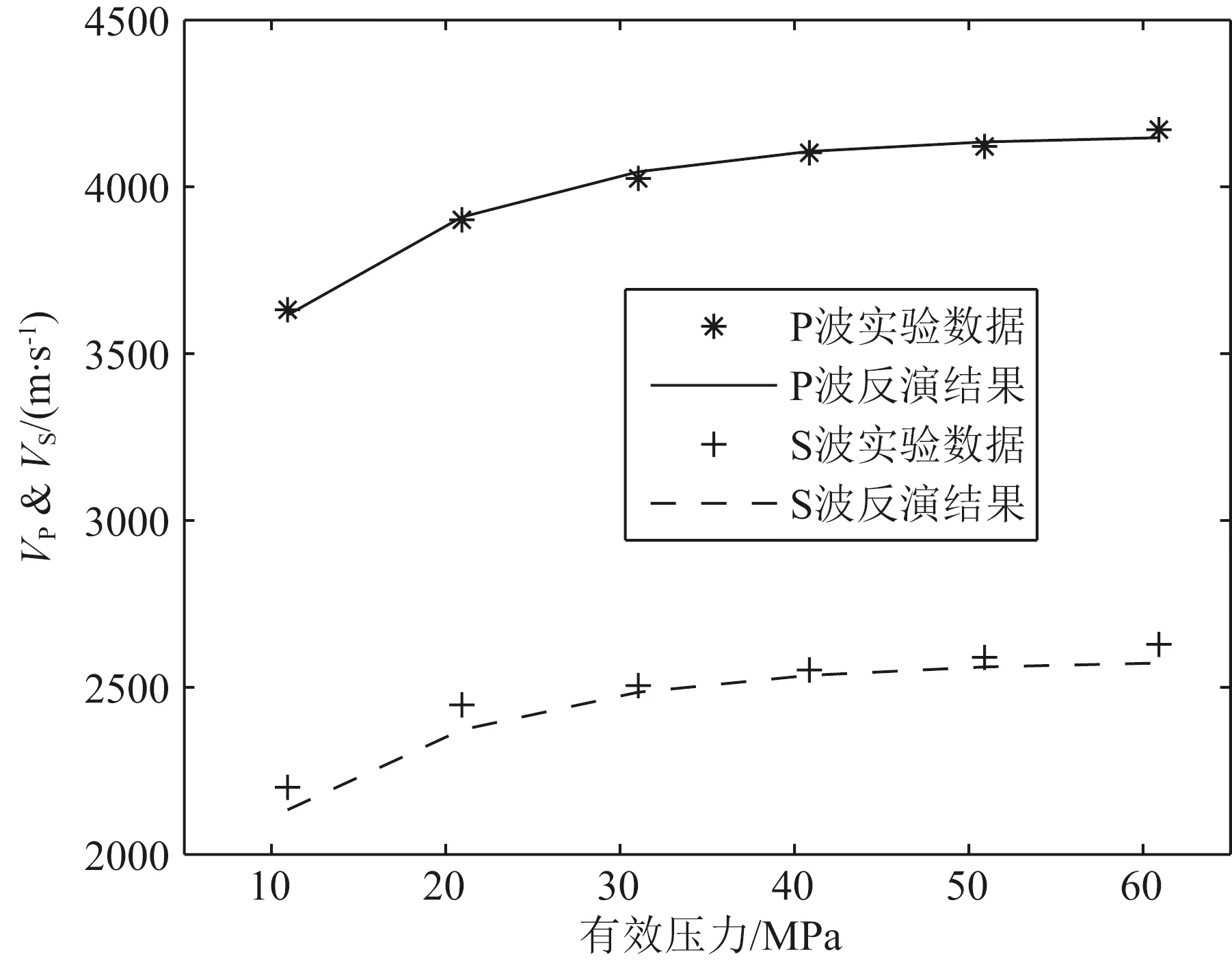
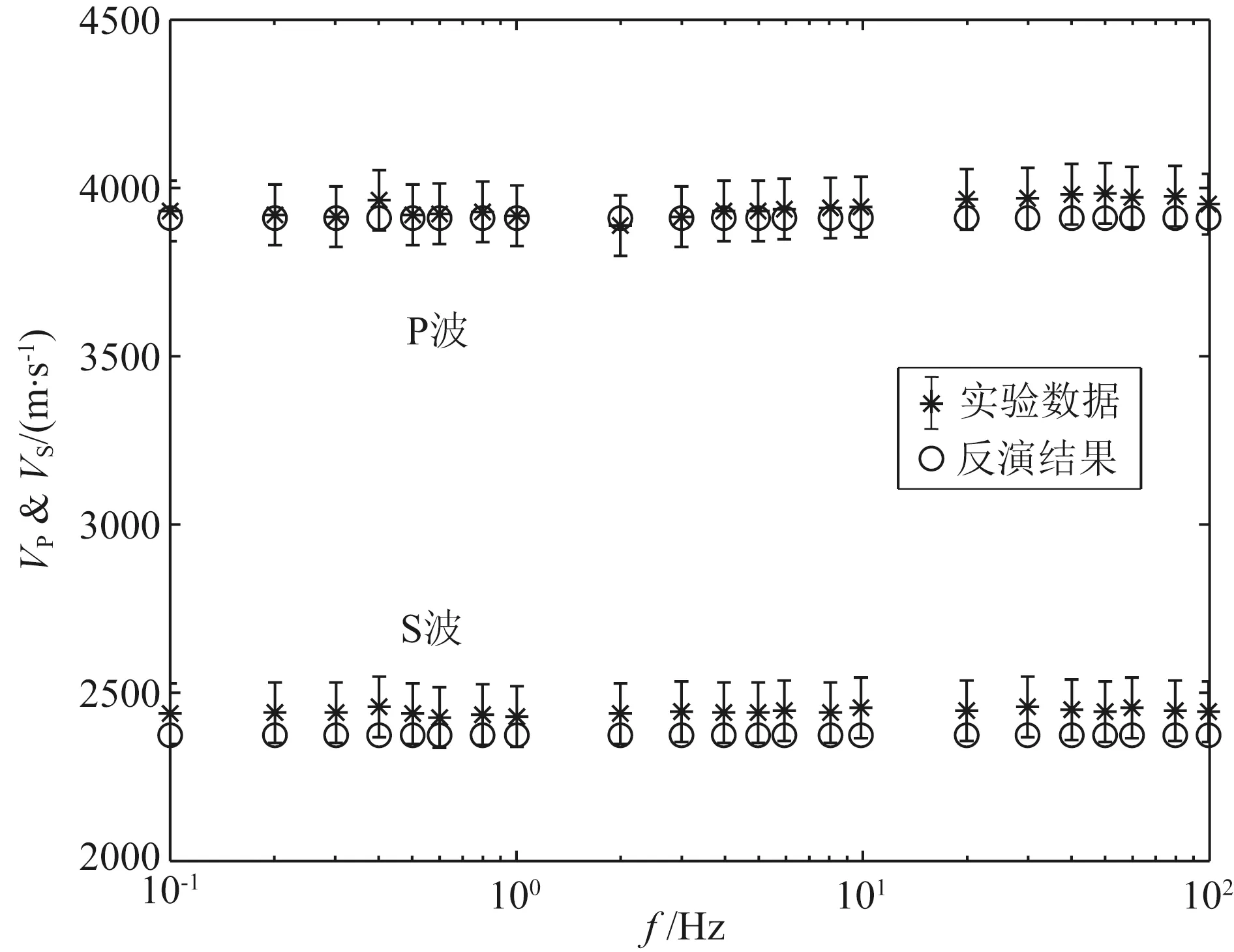
种群个体数量设置为40,初始交叉概率为0.85,初始变异概率为0.1,新一代个体保留上一代的10%的精英个体,限制每个个体被选中的次数为4次.待反演参数的取值范围分别是:0 图5 岩石干骨架的P波和S波速度随有效压力变化的实验数据与从反演结果计算的曲线的比较Fig.5 Comparison of experimental data of dry rock P-wave and S-wave velocity changing with effective pressure and calculated data using inversion results Vpdry=4188.755-1419.161exp(-0.0791Peff), Vsdry=2630.520-1050.705exp(-0.0760Peff). (8) P波数据和S波数据反演结果的适应值分别为0.9990,0.9985.反演结果和实测数据的比较如图5所示,最大的相对误差为1.69%,说明反演结果和实验数据吻合得非常好. 为了比较自适应遗传算法与传统遗传算法的反演效果,我们同时采用传统遗传算法对Mikhaltsevitch等(2014)的干岩石随有效压力变化的数据进行了反演,并在图6中展示了两种算法的目标函数(公式(6))收敛过程.在图6中,横坐标表示迭代次数,纵坐标表示目标函数值;图6a和6b分别给出了反演P波和S波速度数据时的目标函数收敛过程.从图6中可见,随着迭代步数的增加,目标函数值趋于稳定.在P波和S波数据的反演过程中,自适应杂交遗传算法的目标函数值一直小于传统遗传算法的目标函数值,在趋于稳定之后,自适应杂交遗传算法得到了比传统遗传算法更精确的反演结果.这表明,自适应杂交遗传算法比传统遗传算法精度更高,收敛速度更快. 下面应用多相流Biot理论对水和二氧化碳饱和岩石的P波和S波随有效压力变化数据进行反演.根据Mikhaltsevitch等(2014),实验时岩心的温度为315.15 K,孔隙压力为10 MPa,实验进行时有效压力从10 MPa增加到60 MPa.岩石孔隙度为φ=0.1154,渗透率k=0.28 mD,岩石矿物的密度为ρs=2593.3 kg·m-3,矿物模量为Ks=31.7 GPa,固流耦合密度使用ρa=(α-1)φρf计算,曲折度为1.7,波的频率为0.5 MHz.岩石干骨架的体积模量可以由(8)式和岩石干骨架的密度计算得到.在实验的温度和孔隙压力条件下,水的密度为995.72 kg·m-3,声速为1549.4 m·s-1,黏度为6.3019×10-4Pa·s;CO2的密度为582.0 kg·m-3,声速为248.7 m·s-1,黏度为4.3×10-5Pa·s(Linstrom and Mallard,2001).二氧化碳的饱和度为0.6,水饱和度为0.4,由此计算混合流体的密度为747.5 kg·m-3,黏度为1.2585×10-4Pa·s.给定上述参数,我们来反演混合流体的体积模量.类似于(6),定义目标函数为 图6 目标函数的收敛过程(a) P波的反演过程;(b) S波的反演过程.Fig.6 Convergence process of the objective function(a) Inversion process of P-waves;(b) Inversion process of S-wave. minE(Kf)= (9) 适应值函数与(7)式的构造方式相同.种群个体数设置为60,其余参数和前例相同.待反演的混和流体体积模量的取值范围很自然地规定为CO2和水的体积模量形成的区间,即36 MPa≤Kf≤2.39 GPa.使用自适应杂交遗传算法得到的反演结果为Kf=695.12 MPa,适应值为0.9974.由公式(2)计算的Ruess平均和Voigt平均分别为59.4 MPa和977.8 MPa,而反演结果处于二者之间,这表明了反演结果的合理性.图7比较了用反演结果计算的波速和实验数据,其中横坐标表示有效压力,纵坐标表示波速.从图7可见,由反演结果计算的波速能够很好地拟合实验数据,通过计算可得P波速度的最大相对误差为0.56%,S波速度的最大相对误差为3.06%.这样的结果说明含多相流的Biot理论能够很好地解释水和CO2饱和的Donnybrook砂岩的速度数据. Mikhaltsevitch等(2014)还测量了同一岩石样本(40%水和60%CO2)的低频频散数据.我们将上面反演得到的混和流体体积模量结果应用于解释这组低频频散数据.图8对比了快P波和S波的低频频散实验数据和用反演结果计算的低频频散数据,其中星形表示实验数据,圆圈表示由反演结果计算的结果.图8表明,使用反演结果计算的快P波波速和实验数据拟合得非常好(最大相对误差约为1.85%),而S波的计算结果与实验数据的偏差比快P波要大一些(最大相对误差约为3.45%),但仍然处在实验数据的误差范围以内.这说明反演的混和流体体积模量结果和多相流Biot理论能够很好地描述同时含有水和二氧化碳的Donnybrook砂岩的低频频散数据. 图7 水和二氧化碳饱和岩石的快P波和S波波速随有效压力变化的实验数据和反演结果的比较Fig.7 Comparison of experimental data of fast P-wave and S-wave velocity changing with effective pressure of the rock saturated with water and CO2 and calculated data using inversion results 图8 水和二氧化碳饱和岩石的快P波和S波低频频散数据和反演结果的比较Fig.8 Comparison of low-frequency dispersion data of fast P-wave and S-wave of the rock saturated with water and CO2 calculated data using inversion results 3.2 对二氧化碳地震监测数据的反演 挪威Sleipner气田的二氧化碳封存项目是世界上第一个大规模商业性的封存项目.从1996年开始,二氧化碳被注入到深800~1100 m的Utsira深部咸水层中.为了封存的安全性,四维地震技术被用来监测储层中二氧化碳的分布变化.封存之前的地震调查于1994年进行,之后的1999、2001、2002、2004、2006和2008年分别进行了三维地震调查.对四维地震数据进行研究获得的结果清晰表明,注入的二氧化碳对深部咸水层的地震剖面有十分明显的影响.Sleipner封存项目是成功运用四维地震技术的典型例子(Queißer and Singh,2013). Queißer 和 Singh(2013)应用非线性全波形反演方法对Sleipner气田的二氧化碳封存区域的一个2D垂直剖面的地震数据进行了反演研究,获得了1994、1999和2006年的P波速度剖面图.反演结果显示深部咸水层P波波速剖面有显著的变化,标志着封存的二氧化碳分布的变化.我们应用含多相流的Biot方程和自适应杂交遗传算法对Queißer 和 Singh(2013)中的深部咸水层P波速度剖面进行储层参数反演,以得到1999和2006年二氧化碳饱和度的分布.深部咸水层的砂岩储层中夹杂了数层泥岩,对CO2上浮形成障碍,有利于封存.根据Queißer和Singh(2013),Utsira砂岩的平均孔隙度φ=0.35,渗透率k=2000 mD,矿物模量Ks=40 GPa,干骨架体积模量Kdry=1.37 GPa,剪切模量μdry=0.85 GPa.泥岩的平均孔隙度φ=0.18,渗透率k=6 mD,矿物模量Ks=20 GPa,干骨架体积模量Kdry=4.7 GPa,剪切模量μdry=0.99 GPa.岩石矿物的密度ρs=2600 kg·m-3.储层的温度从顶部的29 ℃增加到底部的39.3 ℃,孔隙压力从顶部的7.9 MPa增加到底部的10.8 MPa,从地震监测数据中得到地震波的主频为38 Hz. 根据Queißer 和 Singh(2013)可知储层由砂岩和泥岩共同组成,所以岩石的等效模量可以通过砂岩和泥岩的模量相对于各自体积分数的Backus平均来计算(Mavko et al.,2003).另外由于泥岩的渗透率非常低(只有6 mD),所以流体替换主要在砂岩中发生,故反演CO2饱和度只在砂岩中进行.我们的反演按如下过程进行:利用Backus平均,根据1994年的速度剖面逐点反演砂岩的体积分数;然后对1999年和2006年的速度剖面逐点反演CO2饱和度,在计算P波速度时利用了之前反演得到的砂岩体积分数以及Backus平均.反演得到的1999年和2006年的饱和度结果如图9所示.从图9可以看出,CO2的分布明显形成层状结构,体现出Utsira深部咸水层中砂岩的层状结构;通过与Queißer和Singh(2013)中的速度剖面图进行比较,可以发现含CO2饱和度高的区域与1999、2006年的速度剖面相对于1994年变化较大的区域相吻合,说明了反演结果的正确性;对比1999年和2006年的CO2分布,可以发现有明显变化的区域也对应于速度剖面发生变化的区域,这说明反演算法能够正确反演CO2饱和度分布的变化.通过对Sleipner实际封存项目的地震监测数据进行反演研究,表明了含多相流的Biot理论和自适应杂交遗传算法在二氧化碳封存问题上的有效性.需要注意的是,Biot理论有其适用范围,只有当储层岩石的频散和衰减属性符合Biot理论的预测时,才可以应用Biot理论进行储层参数反演.在实际问题中,需要根据储层岩石本身的属性选择合适的岩石物理模型. 图9 (a)1999年和(b)2006年的CO2饱和度反演结果Fig.9 Inversion results of CO2 saturation of(a)year 1999 and (b)year 2006 本文以Biot理论为基础,结合多相流模型,研究了孔隙度、CO2饱和度、温度和压力等参数对同时含有水和二氧化碳的孔隙介质中快P波和S波波速和衰减等属性的影响.数值模拟结果表明,孔隙度和二氧化碳饱和度对岩石的频散和衰减属性影响强烈,而温度和压力的变化通过孔隙流体性质对岩石的波速产生影响.对于孔隙储层,二氧化碳的饱和度是决定波速最直接和最重要的因素之一.数值实验表明,当CO2饱和度发生变化,波的各种属性也会发生显著的变化,正因为如此才使地震监测成为可能.同时,由于二氧化碳的物理性质(密度、声速、黏度等)对温度和压力很敏感,所以这两个物理参数也是决定波速的重要因素.另一方面,我们应用含多相流的Biot理论和自适应杂交遗传算法对岩心实验数据和低频频散数据进行了反演.结果显示,岩石干骨架的波速以及水和二氧化碳饱和岩石的波速随有效压力变化数据的反演结果和实验数据拟合得很好、频散数据的反演结果和实验数据非常接近,可很好地用于解释水和二氧化碳饱和的Donnybrook砂岩的波速随有效压力的变化.此外,我们将含多相流的Biot理论和自适应杂交遗传算法用于反演Sleipner二氧化碳封存项目的四维地震数据,获得了1999年和2006年的CO2饱和度分布.CO2的饱和度反演结果和地震监测数据十分吻合,CO2饱和度高的区域很好地对应于波速发生较大变化的区域,同时反演结果也反映出CO2饱和度随时间变化的现象.总之,这些反演研究表明了含多相流的Biot理论和自适应杂交遗传算法的正确性和有效性,能够用于地震监测数据的储层参数反演.这对于二氧化碳封存的四维地震监测具有重要意义,可以实现封存后二氧化碳分布的动态监测. 附录 Biot理论的频散和衰减关系 Biot理论的两种P波(快P波和慢P波)的波速和逆品质因子为(杨磊,2014) 其中: 其中A,B,C分别为 B= 其中Mdry=Kdry+4μdry/3为纵波模量,ρ1=(1-φ)ρs,ρ2=φ ρf,ω为角频率,ωc=η φ/kρf为特征频率.其他参数与第2节中定义相同. S波的波速和逆品质因子为 其中: Azuma H,Konishi C,Nobuoka D,et al.2011.Quantitative CO2saturation estimation from time lapse sonic logs by consideration of uniform and patchy saturation.Energy Procedia,4:3472-3477. Bachu S.2008.CO2storage in geological media:role,means,status and barriers to deployment.Progress in Energy and Combustion Science,34(2):254-273. Bergmann P,Diersch M,Götz J,et al.2016.Review on geophysical monitoring of CO2injection at Ketzin,Germany.Journal of Petroleum Science and Engineering,139:112-136. Biot M A.1956a.Theory of propagation of elastic waves in a fluid-saturated porous solid:I.Low-frequency range.J.Acoust.Soc.Am.,28(2):168-178. Biot M A.1956b.Theory of propagation of elastic waves in a fluid-saturated porous solid:II.Higher-frequency range.J.Acoust.Soc.Am.,28(2):179-191. Birkholzer J T,Zhou Q L,Tsang C F.2009.Large-scale impact of CO2storage in deep saline aquifers:a sensitivity study on pressure response in stratified systems.International Journal of Greenhouse Gas Control,3(2):181-194. Brie A,Pampuri F,Marsala A F,et al.1995.Shear sonic interpretation in gas-bearing sands.∥SPE Annual Technical Conference and Exhibition.Dallas,Texas:SPE,701-710. Carcione J M,Picotti S,Gei D,et al.2006.Physics and seismic modeling for monitoring CO2storage.Pure and Applied Geophysics,163(1):175-207. Chadwick R A,Noy D,Arts R,et al.2009.Latest time-lapse seismic data from Sleipner yield new insights into CO2plume development.Energy Procedia,1(1):2103-2110. Doughty C.2007.Modeling geologic storage of carbon dioxide:comparison of non-hysteretic and hysteretic characteristic curves.Energy Conversion and Management,48(6):1768-1781. Eberhart-Phillips D,Han D H,Zoback M D.1989.Empirical relationships among seismic velocity,effective pressure,porosity,and clay content in sandstone.Geophysics,54(1):82-89. Fang Z L,Yang D H.2015.Inversion of reservoir porosity,saturation,and permeability based on a robust hybrid genetic algorithm.Geophysics,80(5):R265-R280. Gassmann F.1951.Elastic waves through a packing of spheres.Geophysics,16(4):673-685. Gaus I,Audigane P,André L,et al.2008.Geochemical and solute transport modelling for CO2storage,what to expect from it? International Journal of Greenhouse Gas Control,2(4):605-625. Hao Y J,Yang D H.2012.Research progress of carbon dioxide capture and geological sequestration problem and seismic monitoring research.Progress in Geophys.(in Chinese),27(6):2369-2383,doi:10.6038/j.issn.1004-2903.2012.06.012. Hovorka S D,Benson S M,Doughty C,et al.2006.Measuring permanence of CO2storage in saline formations:the Frio experiment.Environmental Geosciences,13(2):105-121. Lebedev M,Pervukhina M,Mikhaltsevitch,V,et al.2013.An experimental study of acoustic responses on the injection of supercritical CO2into sandstones from the Otway Basin.Geophysics,78(4):D293-D306. Lei X L,Xue Z Q.2009.Ultrasonic velocity and attenuation during CO2injection into water-saturated porous sandstone:Measurements using difference seismic tomography.Physics of the Earth and Planetary Interiors,176(3-4):224-234. Linstrom P J,Mallard W G.2001.NIST Chemistry webbook;NIST standard reference database No.69.http:∥webbook.nist.gov/chemistry/. Lumley D.2010.4D seismic monitoring of CO2sequestration.The Leading Edge,29(2):150-155. MacBeth C,Floricich M,Soldo J.2006.Going quantitative with 4D seismic analysis.Geophysical Prospecting,54(3):303-317. Mathieson A,Midgely J,Wright I,et al.2011.In Salah CO2storage JIP:CO2sequestration monitoring and verification technologies applied at Krechba,Algeria.Energy Procedia,4:3596-3603. Mavko G,Mukerji T,Dvorkin J.2003.The Rock Physics Handbook:Tools for Seismic Analysis of Porous Media.Cambridge:Cambridge University Press.Metz B,Davidson O,De Coninck H C,et al.2005.IPCC special report on carbon dioxide capture and storage. Prepared by Working Group III of the Intergovernmental Panel on Climate Change.Cambridge,United Kingdom and New York,NY,USA:Cambridge University Press. Michael K,Golab A,Shulakova V,et al.2010.Geological storage of CO2in saline aquifers—a review of the experience from existing storage operations.International Journal of Greenhouse Gas Control,4(4):659-667. Mikhaltsevitch V,Lebedev M,Gurevich B.2014.Measurements of the elastic and anelastic properties of sandstone flooded with supercritical CO2.Geophysical Prospecting,62(6):1266-1277. Nakagawa S,Kneafsey T J,Daley T M.2013.Laboratory seismic monitoring of supercritical CO2flooding in sandstone cores using the Split Hopkinson Resonant Bar technique with concurrent x-ray Computed Tomography imaging.Geophysical Prospecting,61(2):254-269. Pruess K.2005.Numerical studies of fluid leakage from a geologic disposal reservoir for CO2show self-limiting feedback between fluid flow and heat transfer.Geophysical Research Letters,32(4):L14404. Queißer M,Singh S C.2013.Full waveform inversion in the time lapse mode applied to CO2storage at Sleipner.Geophysical prospecting,61(3):537-555. Rutqvist J,Börgesson L,Chijimatsu M,et al.2001.Thermohydromechanics of partially saturated geological media:governing equations and formulation of four finite element models.International Journal of Rock Mechanics and Mining Sciences,38(1):105-127. Shi J Q,Xue Z Q,Durucan S.2011.Supercritical CO2core flooding and imbibition in Tako sandstone—Influence of sub-core scale heterogeneity.International Journal of Greenhouse Gas Control,5(1):75-87. Siggins A F,Lwin M,Wisman P.2010.Laboratory calibration of the seismo-acoustic response of CO2saturated sandstones.International Journal of Greenhouse Gas Control,4(6):920-927. Yang L.2014.Wave dispersion and attenuation in elastic and viscoelastic media with multiphase flow and its applications [Ph.D.Thesis].Beijing:Tsinghua University. Yang L,Yang D H,Hao Y J,et al.2014.A study on inversion of reservoir parameters under coupling interaction of multiple physical mechanisms.Chinese J.Geophys.(in Chinese),57(8):2678-2686,doi:10.6038/cjg20140826. Zhang F J,Juhlin C,Ivandic M,et al.2013.Application of seismic full waveform inversion to monitor CO2injection:Modelling and a real data example from the Ketzin site,Germany.Geophysical Prospecting,61(S1):284-299. Zhang Y,Nishizawa O,Kiyama T,et al.2015.Saturation-path dependency of P-wave velocity and attenuation in sandstone saturated with CO2and brine revealed by simultaneous measurements of waveforms and X-ray computed tomography images.Geophysics,80(4):D403-D415. Zhao J G,Tang G Y,Deng J X,et al.2013.Determination of rock acoustic properties at low frequency:A differential acoustical resonance spectroscopy device and its estimation technique.Geophysical Research Letters,40(12):2975-2982. 附中文参考文献 郝艳军,杨顶辉.2012.二氧化碳地质封存问题和地震监测研究进展.地球物理学进展,27(6):2369-2383,doi:10.6038/j.issn.1004-2903.2012.06.012. 杨磊.2014.含多相流弹性及粘弹性介质中波频散与衰减分析及其应用[博士论文].北京:清华大学. 杨磊,杨顶辉,郝艳军等.2014.多种物理机制耦合作用下的储层介质参数反演研究.地球物理学报,57(8):2678-2686,doi:10.6038/cjg20140826. (本文编辑 张正峰) Reservoir parameter inversion of CO2geological sequestration based on the self-adaptive hybrid genetic algorithm HAO Yan-Jun1,YANG Ding-Hui1*,Cheng Yuan-Feng2 1 Department of Mathematical Sciences,Tsinghua University,Beijing 100084,China2 Shengli Geophysical Research Institute of SINOPEC,Shandong Dongying 257001,China Carbon dioxide geological sequestration is an important approach to reduce carbon emission and to mitigate global warming.An important part of CO2sequestration is seismic monitoring,which is to monitor carbon dioxide distribution variation using the seismic method after sequestration.To achieve this goal,we need to establish the relationship between reservoir parameters and seismic properties (rock physics model),and to obtain parameters like reservoir fluid saturation through inversion of seismic monitoring data.First,based on the Biot model and multiphase model,we investigate the effects of several physical parameters (porosity,CO2saturation,temperature and pressure,et al.) on seismic properties such as wave velocity and attenuation of carbon dioxide and water saturated porous media to obtain the regular understanding.The results show that porosity and CO2saturation have a huge impact on the properties of wave dispersion and attenuation,and temperature and pressure can affect the rock velocity through the properties of porous fluids.Next,based on Biot theory with multiphase flow,we apply the self-adaptive hybrid genetic algorithm,which has stronger anti-interference capacity and better ability of local search and anti-interference,to perform inversion of actual data.The inversion of core experimental data indicates the validity of the algorithm,and shows that Biot theory with multiphase flow can explain the wave velocity characters of CO2and water saturated rock.At last,we apply the self-adaptive hybrid genetic algorithm to the seismic monitoring data of actual sequestration project,and obtain the CO2saturation distribution at different periods after sequestration and achieved the purpose of using the seismic method to monitor carbon dioxide distribution. Carbon dioxide geological sequestration;Biot theory;Multiphase flow;Genetic algorithm;Reservoir parameter inversion 郝艳军,杨顶辉,程远锋.2016.基于自适应杂交遗传算法的CO2地质封存的储层参数反演研究.地球物理学报,59(11):4234-4245, 10.6038/cjg20161125. Hao Y J,Yang D H,Cheng Y F.2016.Reservoir parameter inversion of CO2geological sequestration based on the self-adaptive hybrid genetic algorithm.Chinese J.Geophys.(in Chinese),59(11):4234-4245,doi:10.6038/cjg20161125. 国家基金重大项目(41390452)的资助. 郝艳军,男,1986年生,清华大学数学科学系博士研究生,主要研究方向为二氧化碳地质封存的数学物理模型及其求解.E-mail:haoyanjun@tsinghua.org.cn *通讯作者 杨顶辉,教授,主要从事计算地球物理、孔隙介质波传播理论等研究.E-mail:dhyang@math.tsinghua.edu.cn 10.6038/cjg20161125 P631 2016-02-11,2016-09-12收修定稿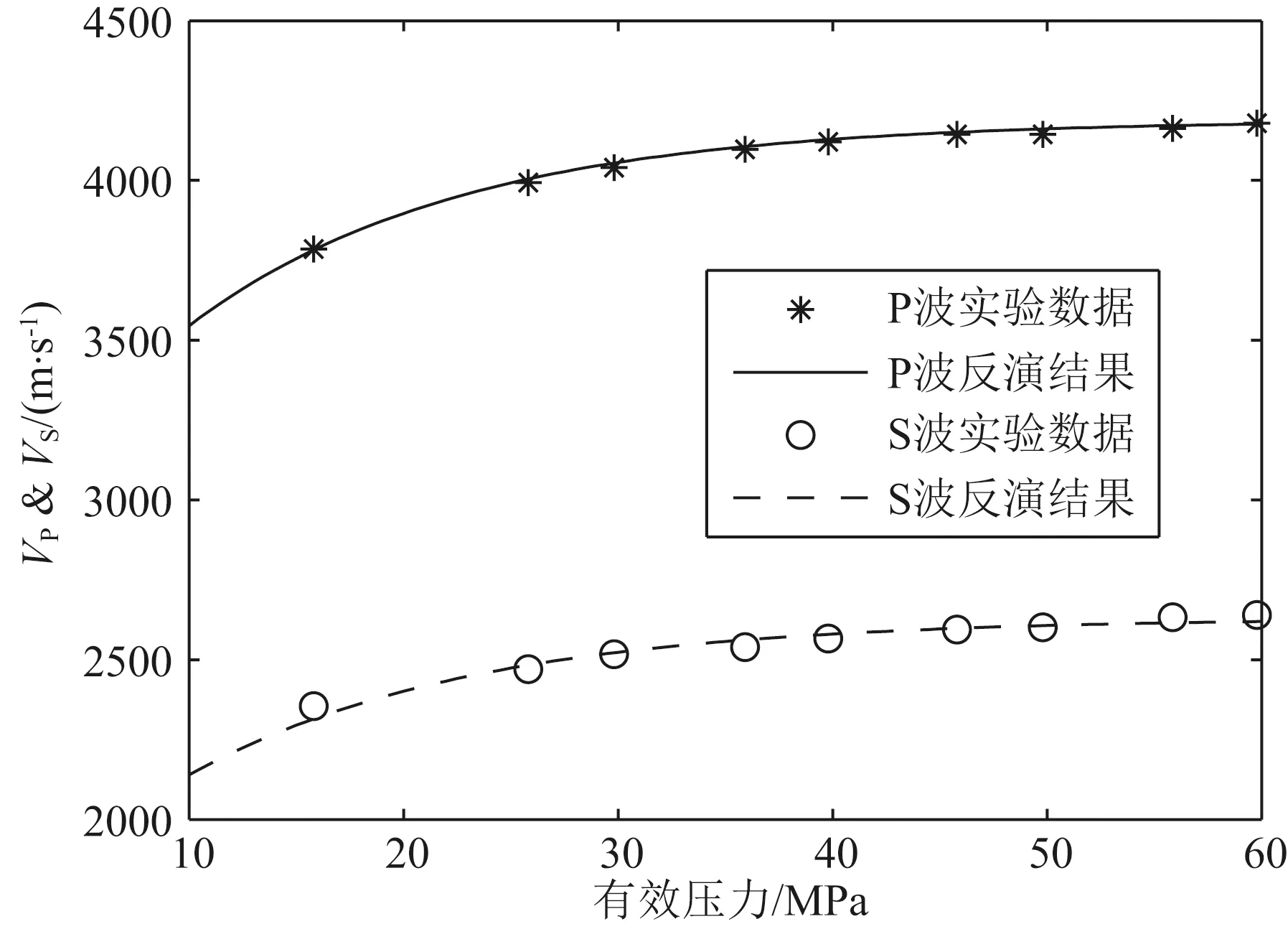

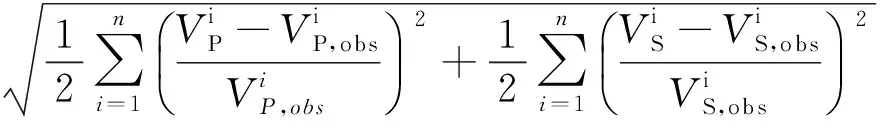

4 讨论和结论