基于ABAQUS的马鞍形曲面板材渐进折弯成形研究*

付泽民 徐 佳 赵志繁 于晓龙 王佳炜

(上海应用技术大学，上海 201418)



基于ABAQUS的马鞍形曲面板材渐进折弯成形研究*

付泽民 徐 佳 赵志繁 于晓龙 王佳炜

(上海应用技术大学，上海 201418)

为改善大幅面曲面板材成形精度，提出一种渐进折弯成形新方法。以马鞍形曲面成形为例，采用平面应变和Mises各向同性屈服准则，建立基于ABAQUS/Explicit & Standard 求解分析平台的板材三维弹塑性渐进折弯成形有限元模型，对板材渐进折弯与回弹全过程进行了数值模拟，结合试验研究，获得最优工艺参数。模拟及实验结果表明：采用曲面凸凹模及优化工艺参数可实现高精度大幅面曲面板材的成形，模拟成形工件的平均误差为+2.1/-1.8 mm，实验测量成形板材曲率与目标模型理论曲率误差较小，模拟结果与实验结果基本吻合，这对曲面冷弯成形技术的应用，具有重要的参考价值和指导意义。

曲面板材；渐进折弯；有限元模型；工艺参数

板材折弯是一种曲面成形的重要方法，大多数折弯是成形等截面的曲面，对于大幅面复杂曲面的成形难以通过直线凸凹模渐进折弯成形[1]。本文提出采用曲面凸凹模的渐进折弯成形新方法，是一种柔性的板材成形方法，它将板材逐道次地送入曲面凸凹模之间，如此多道次地进行压弯，每道次板材的进给量和凹模的下压量参数严格控制，这样渐进地成形三维曲面。这种成形方法尤其适合船舶、飞机、建筑等产业的复杂曲面板材中小批量新产品的开发。在板材成形过程中，板材的回弹是十分复杂的问题，表现出高度的非线性，对成形质量影响较大。目前，国内外许多学者在回弹分析和工程控制方面做了大量研究，取得了大量成果[2-4]。付泽民等[5]曾用量纲分析法建立了板材单一道次折弯回弹数学模型，对多道次的曲面渐进折弯有其局限性。随着计算机技术的迅速发展，有限元数值模拟技术应用到折弯成形领域，研究者在本构关系模型、求解算法等方面进行了大量的研究。Minutolo[6]等运用有限元法对板材渐进成形极限进行了分析，Yamashita[7]等用数值模拟方法对工艺路径在渐进成形过程中的影响进行了分析，并以此指导实验，获得了良好的效果。国内外有许多关于板材单道次折弯成形数值模拟研究[8-9]，讨论了不同参数对折弯成形的影响，而对于多道次曲面渐进折弯成形数值模拟研究甚少。因此，为了提高实验效率，减少实验次数，本文通过在ABAQUS有限元分析平台上，建立马鞍形曲面板材的渐进折弯成形有限元模型，采用适合动态和非线性分析的ABAQUS/Explicit显示模块模拟板材成形过程，适合静态和稳态分析的ABAQUS/Standard隐式模块模拟板材的回弹翘曲过程，并结合实验获取最优模具参数及成形工艺参数，达到成形较高质量的马鞍形曲面板材的目的。

1 马鞍形曲面板材渐进折弯成形数值模拟

1.1 渐进折弯成形过程的几何规划

马鞍形是双曲率曲面，横向抛物线形状由曲面凸凹模轮廓控制，纵向由成形工艺控制。图1所示为纵向抛物线形状渐进折弯成形的几何规划，图中序号为凹模每道次下压位置，也是板材每道次的回弹中心位置，半径为750 mm圆心位置为相对应道次理论的回弹圆心位置，第1道为初始位置120 mm，30 mm为板材7和8道次的进给量，70 mm为其他道次板材进给量。

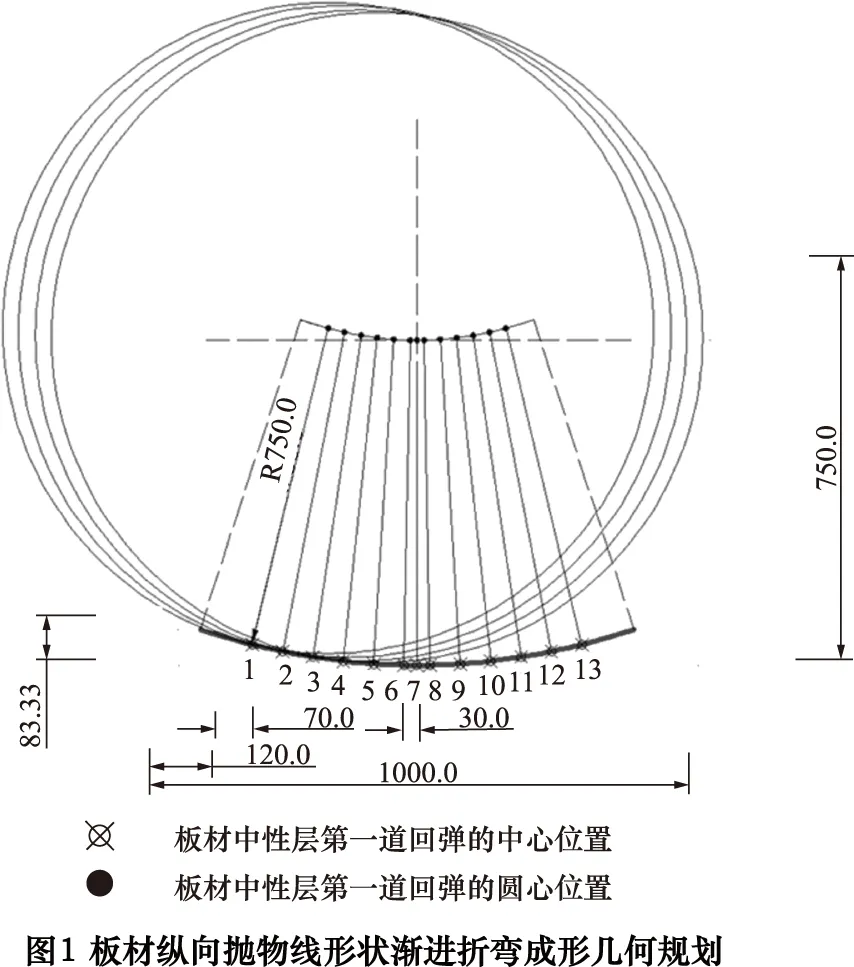
1.2 模拟设置

1.2.1 模具和材料参数

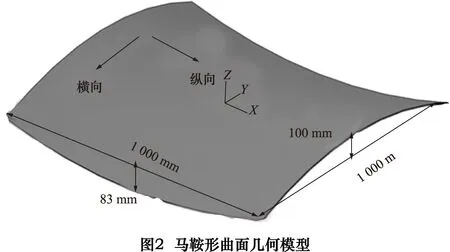
为了获得马鞍形曲面(如图2)，将凸模几何轮廓设计成马鞍形曲面横截面弧线(抛物线)形状。对于凸模开口大小的设计，过小时直线边容易产生翘曲且加工工时长，过大时成形精度差。对于本实验板材成形规格，将凸模开口大小确定为200 mm，圆角半径为5 mm，且两边凸模宽都为50 mm。凹模几何轮廓在横截面上也设计成抛物线形状。因为凹模的纵截面形状也会影响板材纵向弯曲，为了更好的成形，将凹模在纵截面方向上设计成有一定圆弧度的形状，圆弧度半径为750 mm，宽为100 mm。凸凹模长都为1 100 mm，如图3所示。坯料板材规格为4 mm×1000 mm×1000 mm方形，材料型号为Q235B钢板，材料参数：密度7 850 kg/m3，弹性模量207 GPa，屈服极限167 MPa，泊松比为0.28，硬化指数0.23。

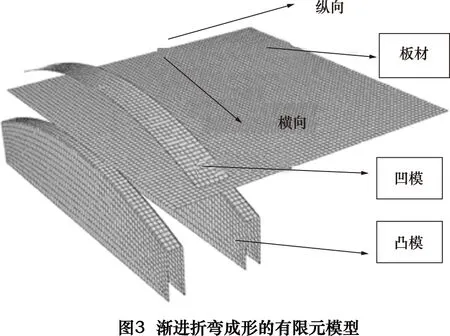
1.2.2 有限元模型

渐进折弯成形过程是复杂的弹塑性变形过程，成形和回弹交替进行，每道次之间相互影响，它是高度非线性问题。为了简化求解过程并快速找到成形规律，采用非线性弹塑性硬化材料模型中Mises各向同性屈服准则材料模型。为缩短计算时间，模具和板材都用壳形状建模，使用解析刚体模型代表模具，变形体模型代表板材。对于大幅面板材折弯过程，采用平面应变假设，并忽略厚度方向的应力，用结构化网格划分技术将板材划分为4 624个节点和4 489个单元(ABAQUS type S4R，称为四节点四边形减缩积分壳单元)，板材与凹凸模接触条件采用通用接触算法、罚函数接触力算法以及库伦摩擦定律，各接触部件间摩擦系数设置为0.12，有限元模型如图3所示。

1.3 模拟获得的优化工艺参数

由于每道次凹模下压后两边翘起程度和变形程度都不同，每道次之间相互影响，并且每道次卸载后回弹量也不同，所以要提高成形精度，下压量是一个非常重要的工艺参数。根据马鞍形曲面性质，此例纵向截面抛物线方程为X2=3 000×Z，由模拟得到较好的工艺参数如表1所列，其中凹模的中性层到凸模中性层的垂直距离为150 mm，将此位置作为初始位置。

采用顺序折弯将13道次成形及回弹模拟完成(如图4)，可以看出前面几道次的位置翘曲的厉害，因此还需要进行重复的成形和修正，此后的成形可以适当地增加进给量，并根据每道次回弹后的成形效果进行下一道次下压量的微调，以得到最好的成形效果。

2 数值模拟结果及分析

2.1 采用有限元方法基于ABAQUS的最终数值模拟结果

最终的数值模拟结果如图5所示，分别为最终的成形模拟和回弹模拟结果，可以看出具有较好的成形效果，但有一定的压痕缺陷。在渐进折弯成形中压痕缺陷无法避免，可以通过减小板材进给量来减小压痕以获得较光顺的表面。

表1 模拟工艺参数

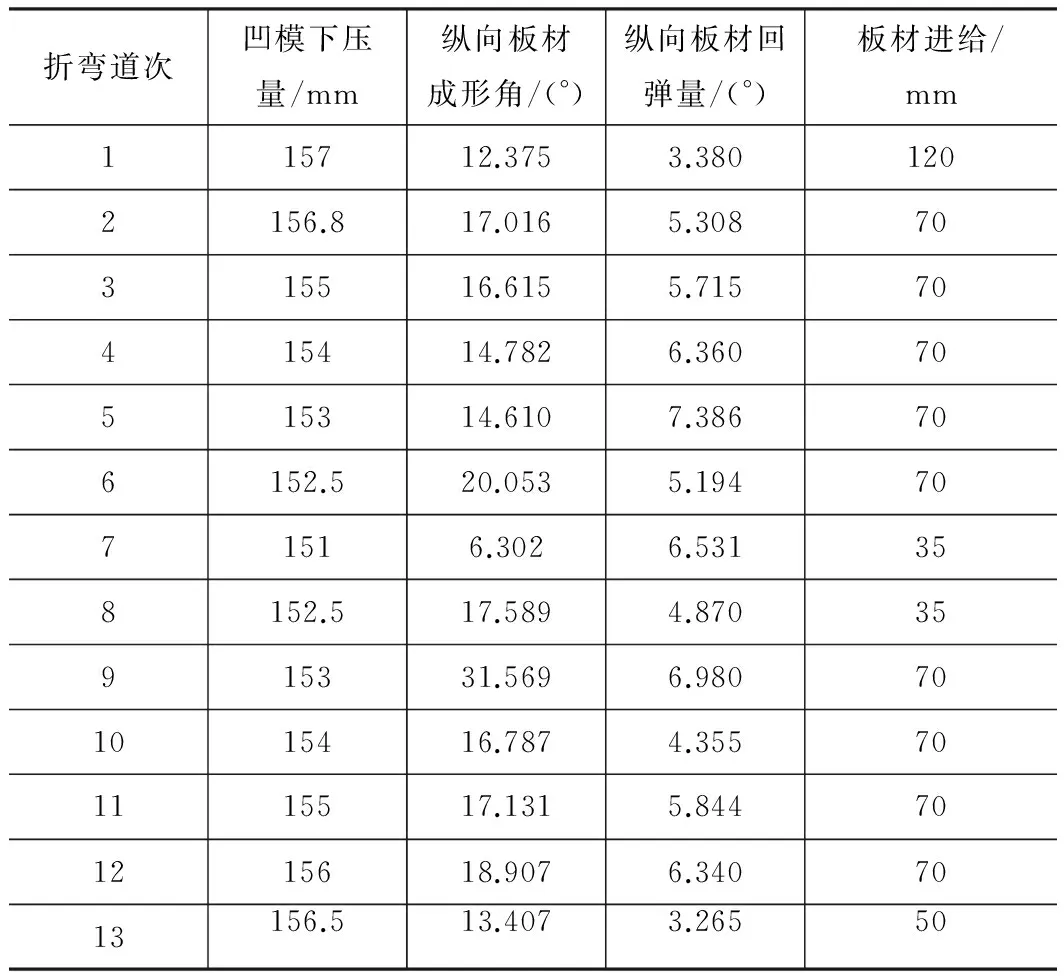
折弯道次凹模下压量/mm纵向板材成形角/(°)纵向板材回弹量/(°)板材进给/mm115712.3753.3801202156.817.0165.30870315516.6155.71570415414.7826.36070515314.6107.386706152.520.0535.1947071516.3026.531358152.517.5894.87035915331.5696.980701015416.7874.355701115517.1315.844701215618.9076.3407013156.513.4073.26550

2.2 应力和应变的变化与分布

表2为各道次的等效应力极值的变化过程，随着道次的增加，基本表现出先增大后减小再增大的过程，在第3道达到最大值194.2 MPa，并且从此道开始翘曲表现较为明显。

表2 各道次等效应力极值的变化过程

道次1234567最大等效应力/MPa192.8193.8194.2194.1194.0194.1191.5道次8910111213最大等效应力/MPa193.2193.6193.3192.1194.1194.1

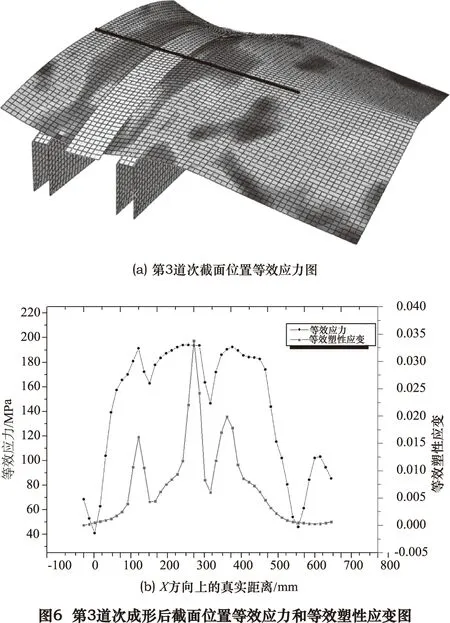
渐进折弯成形过程中，每道次的等效应力分布规律，对提高板材成形质量有重要作用。如图6为第3道次截面位置等效应力图，可以看出，应力峰值位置在凸模边缘和凹模接触区域，此时等效塑性应变也在峰值位置，最大值为0.034，此处容易出现应力集中和断裂失效。

2.3 板材进给量对成形的影响

分别模拟了板材进给量为60 mm、70 mm、80 mm时的结果，通过对比看出，进给量越小，成形质量越好，但是成形效率也就越低，进给量越大成形后误差也就越大。因此，板材渐进折弯成形时应根据成形质量要求，综合考虑成形质量和成形效率，选择适当的进给量。经过模拟成形，此例选择进给量70 mm时，成形质量较好，成形效率较高。如图7为模拟结果与标准马鞍形曲面模型匹配结果。

3 成形实验结果

将凹凸模正确地安装在数控折弯机上，根据数值模拟工艺参数指导渐进折弯成形实验，图8为渐进折弯成形马鞍形曲面实验成形装备及结果。

用半径仪对成形板材边缘进行测量，测得边缘处各部分曲率与目标模型各部分理论曲率的平均误差相差不大，而数值模拟结果经过匹配平均误差更小，为+2.1/-1.8 mm，实验结果与数值模拟结果基本一致，因此渐进折弯成形数值模拟能为实验提供可靠的工艺参数。

4 结语

(1)通过对马鞍形曲面的成形及回弹过程的数值模拟，本文所建立的基于平面应变假设的弹塑性模型具有可靠性，该模型适合三维曲面板材渐进折弯成形及数值模拟，为曲面工件采用曲面凸凹模进行多道次渐进折弯成形的数值模拟分析提供数学模型和参数，提高仿真的真实性和可靠性。

(2)ABAQUS有限元方法用于三维曲面板材多道次渐进折弯成形和回弹过程的模拟具有较高的精度和较好的收敛性。

(3)渐进折弯成形过程中会出现翘曲现象，因此需要重复修正折弯，以提高成形件的成形质量。实验表明，数值模拟结果与实验结果基本吻合。

[1]Zemin Fu, Dachao Hu, Guangming Liu, et al. Multi-step incremental air-bending forming simulation for U-shaped workpiece with super length and large opening of sheet metal[J]. International Journal of Materials and Product Technology, 2011, 42(3/4): 247-262.

[2]Chen Lei, Yang JiChang, Zhang LiWen. Research on the factors influencing bending springback of sheet metal by FEM[J]. Cailiao Kexue yu Gongyi/Material Science and Technology, 2007, 15(2): 269-272.

[3]Tekaslan O, Gerger N, Seker U. Determination of spring-back of stainless steel sheet metal in “V” bending dies[J]. Materials and Design, 2008, 29(5):1043-1050.

[4]Zemin Fu , Jianhua Mo, Pan Gong, et al. Mould correction for sheet metal multi-step incremental air-bending forming based on close-loop control and FEM simulation[J]. International Journal of Mechanical Sciences, 2009, 51: 732-740.

[5]付泽民, 莫健华, 陈伟, 等. 基于量纲分析法的金属板材折弯回弹数学模型[J]. 机械工程学报,2010, 46(12): 53- 58.

[6]Minutolo, F. Capece, Durante, M, et al. A, Langella A. Evaluation of the maximum slope angle of simple geometries carried out by incremental forming process[J]. Journal of Materials Processing Technology, 2007, 194(1-3):(145-150).

[7]Yamashita Minoru, Gotoh Manabu, Atsumi Shin-Ya. Numerical simulation of incremental forming of sheet metal[J]. Journal of Materials Processing Technology, 2008, 199(1):163-172.

[8]S K Panthi,. Ramakrishnan Pathak,N. et al. Chouhan, J.S. An analysis of springback in sheet metal bending using finite element method (FEM)[J]. Journal of Materials Processing Technology, 2007, 186( 1-3) :(120-124) .

[9]Narayanasamy R, Padmamabhan P. Influence of lubrication on springback in air bending process of interstitial free steel sheet[J]. Journal of Materials Engineering and Performance, 2010, 19(2):246-251.

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Research on incremental air-bending forming of saddle shaped curved plate based on ABAQUS

FU Zemin，XU Jia，ZHAO Zhifan，YU Xiaolong，WANG Jiawei

(Shanghai Institute of Technology, Shanghai 201418,CHN)

In order to improve the forming accuracy of large curved panel, this paper presents a new method of incremental air-bending forming. The saddle surface forming as an example, using the plane strain and Mises isotropic yield criterion, the establishment of ABAQUS/Explicit & Standard analysis platform plate 3D elastic-plastic finite element model based on incremental air-bending forming, the whole process of gradual bending and springback by numerical simulation was carried out based on experimental study, obtain the optimal die parameters and process parameters, simulation and experimental results show that by curved punch forming and optimization of process parameters can be realized large curved plates, the average error of workpiece for +2.1/-1.8mm numerical simulation, experimental measurements of forming plate curvature and curvature theory of target model error is small, the simulation results are in agreement with the experimental results, application the surface cold forming technology, which has important reference value and guiding significance.

curved plate; incremental air-bending; finite-element model; process parameters

* 上海市高等教育内涵建设085 项目( 405ZK136124) ; 上海教委科技创新项目( 14YZ146)

TG386

A

10.19287/j.cnki.1005-2402.2016.11.030

付泽民，男，1966年生，博士，副教授，硕士研究生导师，主要从事塑性加工工艺、模具技术研究。已发表论文20多篇。

(编辑 谭弘颖)

2016-05-24)

161137