基于解相关CEEMD的滚动轴承特征信号提取算法研究*

张永宏 陶润喆 王丽华 谢阳阳

(南京信息工程大学信息与控制学院，江苏 南京 210044)



基于解相关CEEMD的滚动轴承特征信号提取算法研究*

张永宏 陶润喆 王丽华 谢阳阳

(南京信息工程大学信息与控制学院，江苏 南京 210044)

近年来随着时频分析方法希尔伯特黄变换的提出，经验模态分解(Empirical Mode Decomposition, EMD)已经在滚动轴承信号处理中得到了应用。但不管EMD还是其改进的互补总体平均经验模态分解( Complementary Ensemble Empirical Mode Decomposition, CEEMD)，到目前为止依然都存在着模态混叠现象。为了实现特征信号的精确提取，需要对分解后产生模态混叠的部分予以修正，从而保证各固有模态函数(Intrinsic Mode Function, IMF)分量之间互不耦合(即正交)。针对这一问题提出了解相关与CEEMD相结合的算法。该方法首先运用CEEMD自适应分解的能力对信号进行细节的提取，然后对分解后依然存在的少量频率混叠部分利用解相关运算予以修正，实现对特征频率信号的提取，从而解决了频率混叠问题。通过仿真试验验证了该方法的有效性，并将该方法应用于旋转机械振动信号的特征频率成分的提取中，取得很好的效果。

模态混叠；互补总体平均经验模态分解；解相关；特征提取

滚动轴承是旋转机械中应用最广且也是最易损坏的机械零件之一，许多机械故障都与滚动轴承有关，它工作好坏对机械的工作状态有很大的影响，故对工作中的滚动轴承特征频率信号的精确提取尤为重要，为后期的故障诊断奠定基础。由于机械设备振动信号多为非线性非平稳信号，传统的傅里叶分析不免有一定的局限性。时频分析方法如小波变换(wavelet transform, WT)、小波包变换(wavelet package transform, WPT)、Gabor变换、希尔伯特黄变换(hilbert-huang transform,HHT)等，由于能够同时提供信号时域和频域的局部信息，得到广泛的应用。希尔伯特黄变换是由N.E Huang在1998年提出的一种处理和分析非平稳信号的新方法[1]。希尔伯特黄变换中的EMD能将信号自适应分解为有限个IMF，各IMF分量包含原信号不同时间尺度的局部特征信号，因此可以通过对各IMF分量的变化来进行监测。于德介等人就是应用这个原理来进行滚动轴承的状态监测[2]。但EMD最大的缺点是存在严重的模态混叠，不同频率的信号会被自适应地分解到同一IMF内，无法实现对特征频率成分的提取。针对模态混叠的缺点，陈建国等提出了采用独立分量分析(independent component analysis，ICA)方法来进行模态混叠抑制[3]。独立分量分析可有效提高EMD分解得到的IMF分量之间的正交性，但是 ICA具有幅度不确定性，从而会限制对信号的分析及判断。肖瑛等人提出基于解相关的EMD分解[4]，可以有效地对小频率比信号进行分解，但分解过程中需对每个特征频率信号的提取进行多次迭代，且相邻频率成分信号幅值差异较大时分解得到的结果不理想。近年来随着Wu等人[5]通过研究白噪声信号的统计特征，提出了总体平均经验模态分解(ensemble empirical mode decomposition, EEMD)，在抑制模态混叠的问题上更进了一步，但分解后得到的IMF在低频率段依然存在少量的模态混叠，且分解过程中每次添加的白噪声可能会引起重构误差。雷亚国等人根据Wu的算法提出了一种自适应的EEMD并其应用在行星齿轮箱故障检测中[6]，取得了比EEMD更好的分解结果。该方法基于EMD的滤波特性，在提取IMF的过程中自适应改变加入噪声的幅值，并对每个IMF选择不同的筛选次数，有效地削弱了模态混淆，但也大大增加了分解过程的计算量。Yeh等人又在EEMD的基础上提出了新的改进算法CEEMD[7]，有效地解决了EEMD分解可能造成的幅值改变问题。但在实际应用中，想要完全避免模态混叠，实现对各频率信号精确的提取，仍然存在没有完全得到解决的问题[8]。

模态混叠产生的现象是分解得到的IMF分量之间的信息相互耦合，本质上可归结为IMF分量之间不完全正交。根据零均值随机信号之间不相关和正交性等价原理，本文提出了一种对CEEMD分解后依然存在的模态混叠部分，运用解相关运算予以修正的改进算法，保证分解结果各IMF严格的正交，从而实现对旋转机械特征频率信号的精确提取。

1 算法描述

1.1 CEEMD分解

CEEMD 是基于EMD和EEMD提出的一种改进算法。EMD[1]是一种自适应的局部化分析方法，它利用信号的局部特征时间尺度，从原信号中提取出若干阶固有模态函数IMF和一个残余量，分解出的IMF分量突出了数据的局部特征，残余分量体现了信号中的缓慢变化量，从根本上摆脱了傅里叶变换的局限性，非常适用于非平稳、非线性信号的处理。但当信号中含有异常事件时(如间断信号，脉冲等)，EMD会出现模态混叠现象[9]。模态混叠现象是指同一IMF分量包含了不同的尺度分量，这直接导致混叠的IMF缺乏足够的物理意义，致使后续的时频分布混淆。产生模态混叠的原因主要有: ① 信号中存在噪声干扰，改变了信号原本的极值点分布; ② 信号中含有间断高频弱信号的干扰; ③ 混合信号中组合分量的频率过于接近。针对EMD的缺陷，EEMD[5]被提出，其利用白噪声频谱的均匀分布特性，使混入白噪声的信号在不同时间尺度上具有连续性，从而有效地抑制了模态混叠问题，但由于分解时添加的白噪声会引起重构误差，提取的信号幅值会被改变。

故采用CEEMD对信号进行自适应分解效果最好，其与EEMD的主要区别是通过向信号中添加两个相反的白噪声信号，并分别进行EMD分解，从而消除了EEMD分解中添加白噪声的影响。CEEMD具体步骤如下：

(1)分别向被分析信号x(t)中加入等长度的、给定标准差的、一组符号正负相反的正态分布白噪声，形成两个新信号。

(2)应用EMD对加入白噪声后的两个信号分别进行分解，得到其各自的IMF分量。

(3)重复上述(1)、(2)步骤n次，要求每次加入新的随机正态分布白噪声序列。

(4)将每次分解得到的分量共计2n组IMFs对应相加后(如第一次分解的IMF1加上第二次分解IMF1，直到2n组IMF1相加)再分别除以2n求其平均。得到一组IMF分量即为分解结果。

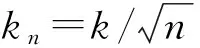
(1)

(2)

仿真信号采样频率为1kHz， 采样时间为1s。

分别采用EMD和CEEMD对仿真信号s(t)进行分解，分解次数为50次，添加白噪声幅值标准差为仿真信号的0.1倍，结果如图1和图2所示。

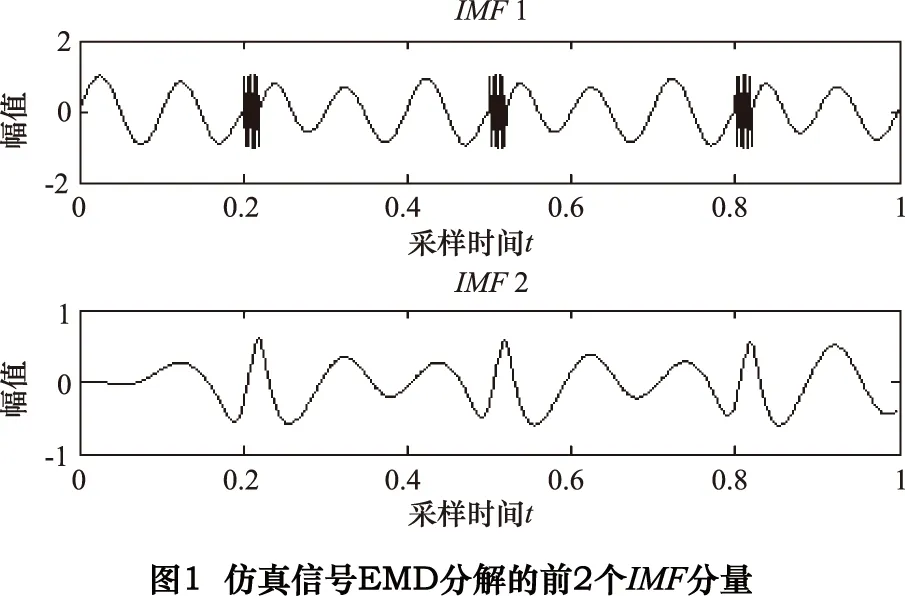
由图1可见，两个频率相差很大的信号被EMD分解到同一个分量即IMF1内，出现了模态混叠现象。

由图2可以看出CEEMD分解得到的IMF1很好地提取出高频间断信号且幅值只有很小的改变；IMF2、IMF3含有少量的两个源信号，出现了少量的模态混叠现象；IMF4提取出低频正弦信号。对IMF1和y2(t)做相关性分析可以达到93.12%。

综上所述，使用CEEMD分解提取特征信号的效果最好。与EMD相比有效地抑制了模态混叠，又降低了EEMD添加随机白噪声对提取分量幅值的影响。但CEEMD在实际分解过程中，低频部分还是有少量的模态混叠部分存在，出现了IMF2和IMF3两个虚假分量，且同一IMF内出现了两个或两个以上的频率分量。

1.2 解相关

CEEMD在实际分解结果中依然存在少量模态混叠，其根本原因可以归结为分解过程中EMD不是严格正交分解，因此导致部分IMF之间信息相互耦合。为了实现特征频率信号的精确提取，对CEEMD分解后存在模态混叠的IMF分量进行修正，保证相邻IMF之间的正交性，是消除CEEMD分解后依然存在模态混叠的一个有效方法。定义两个随机变量x和y，其相关函数：

(3)

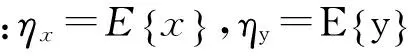
(4)

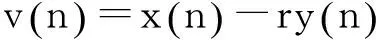
(5)

利用上述解相关算法，可以对CEEMD分解后依然存在模态混叠(尤其是在低频段)的IMF进行修正，使分解得到的相邻的IMF之间不相关，即满足正交性，从而更好地对每个频率成分进行精确的提取。

2 基于解相关的CEEMD算法

对机械设备运行现场采集的振动信号进行CEEMD自适应分解，得到各频率段的IMF分量，若出现模态混叠的部分再利用解相关算法予以修正，使相邻的IMF分量满足正交性，从而达到对特征频率信号的精确提取，即本文提出的改进CEEMD算法。具体算法流程如图3所示。

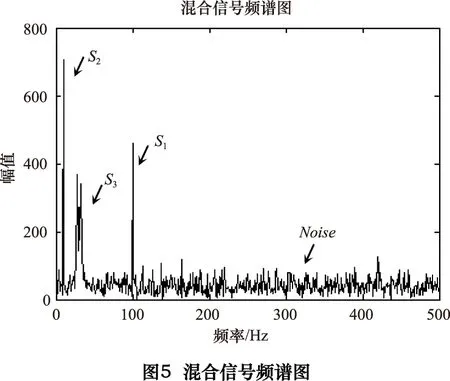
第一步：对采集得到的振动信号做频谱分析，根据频谱图确定信号噪声的大小以及各频率成分的幅值大小。

第二步：根据信号中所含噪声的大小，进行CEEMD重复步骤次数和白噪声幅值的确定，信号内所含噪声越大CEEMD分解时所添加的白噪声幅值越大即倍数越大。本文中选择标准差倍数k为0.1～0.2倍，重复步骤次数n一般选择百以内即可。

第三步：进行CEEMD自适应分解。

第四步：CEEMD分解后各IMF分量自适应提取出各频率信号，对每个IMF做出其频谱图，根据频率与幅值的对应关系检查是否出现频率混叠的部分，并根据式(4)对每个相邻的IMF分量做相关性分析。(可多次实验调整重复步骤次数和幅值标准差，选择特征频率信号所在的相邻的IMF之间相关系数最小的一组作为解相关修正的分量)。

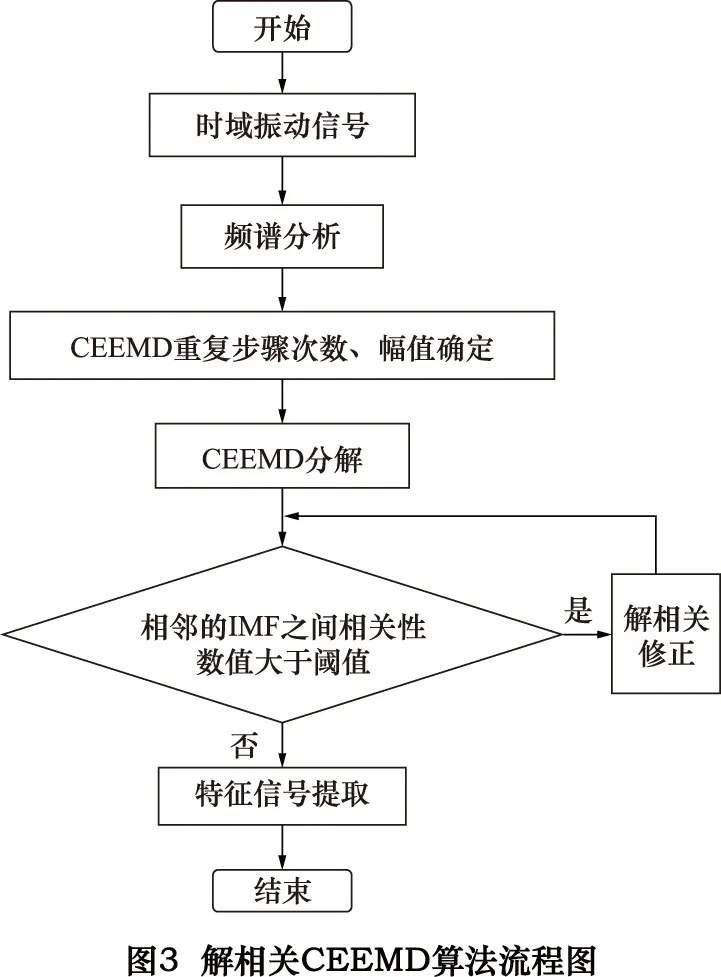
第五步：对特征频率信号所在的相邻IMF分量进行解相关修正，设定阈值λ(阈值可根据自己要求设定)，CEEMD分解后的低频部分的特征频率信号易被分解到相邻的2～3个IMF内，出现少量的模态混叠，故将2～3个IMF从高频到低频逐一修正：

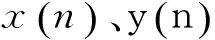
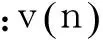
3 仿真实验及工程应用

3.1 仿真实验

3.1.1 混合信号仿真

旋转机械的振动信号中，存在各部件正常工作运行信号、故障信号及环境噪声等多种信号，仿真试验耦合信号组成选取以下4 种基本信号[6]。S1、S2模拟设备正常运行信号；S3模拟碰摩故障发生时的特征信号； Noise模拟噪声信号。设采样频率为1kHz，采样时间为1s，信号模型如式(6)。

(6)

混合信号为Signal=S1+S2+S3+Noise。

正弦信号S1频率为100 Hz，振幅为1(图4a)；余弦信号S2频率为10 Hz,振幅为1.5，初相位为1.5cos(-10)(图4b)；频率为2.5 Hz，振幅为2的正弦信号与频率为30 Hz振幅为1的余弦信号相乘得到的S3(图4c)以及振幅为2.5的随机信号模拟噪声Noise。信号时域波形如图4所示。

3.1.2 解相关CEEMD自适应分解

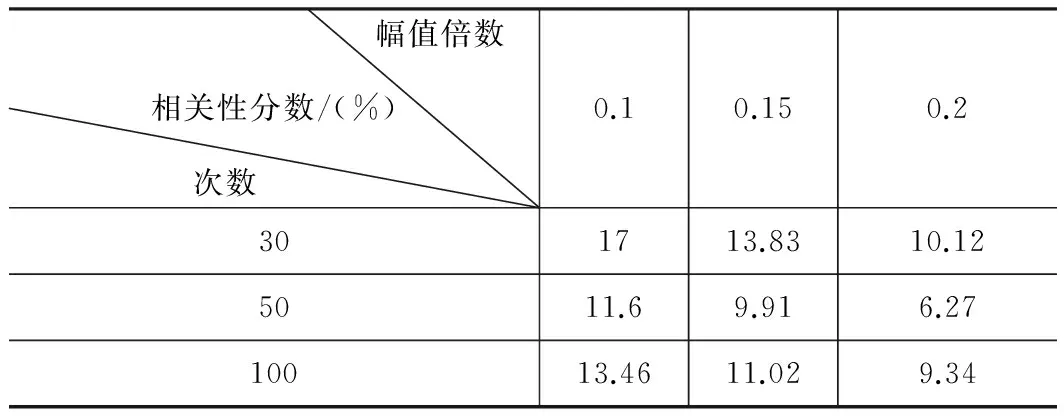
利用解相关CEEMD对仿真信号进行分解，提取特征信号S3。首先为了确定CEEMD的重复步骤次数与加入随机噪声的信号标准差，故作以下实验。选择不同的次数30、50、100次以及不同的信号标准差倍数0.1、0.15、0.2倍。表1记录了不同参数的选择所提取出的特征信号所在的相邻IMF之间的相关性数值(特征信号被S3分解到IMF3和IMF4内)。

表1 迭代次数和噪声幅值选择的相关性分析

幅值倍数相关性分数/(%)次数 0.10.150.2301713.8310.125011.69.916.2710013.4611.029.34

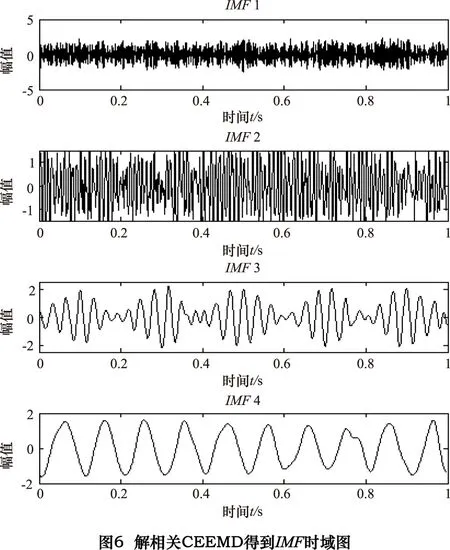
可以由表1看出选择迭代次数为50，信号标准差为仿真信号的0.2倍为最佳，故作为解相关修正的输入。设定阈值λ=0.01，因篇幅关系，在仿真部分直接给出对信号进行解相关CEEMD分解后得到的IMF结果，解相关修正IMF的部分在实际工程应用中再具体说明。解相关CEEMD分解得到的前4个IMF分量如图6所示。

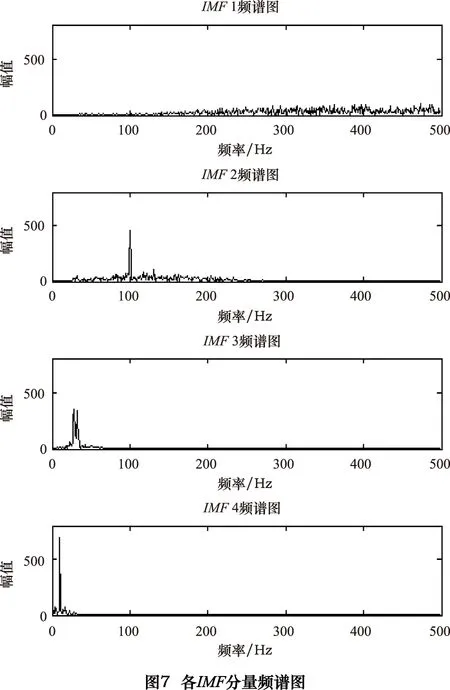
为验证解相关CEEMD分解的效果，检查是否还存在模态混叠部分，对前4个IMF分量做频谱分析，如图7所示。

从图7可以看出各频率信号已经很好地分离，相邻的IMF分量相关性数值都在阈值λ=0.01以下，解相关 CEEMD很好地对特征频率信号S3进行了提取。

3.2 工程应用

采用OROS R3X系的动态信号分析仪对卧式螺旋离心机(简称卧螺离心机)在工作转速运行阶段的振动信号进行测试实验[10]。卧螺离心机相关参数如表2所示。

表2 卧螺离心机主要技术参数

转鼓工作转速转速差功率整机质量外形尺寸n/(r/min)Δn/(r/min)p/kWm/kgl1×l2×l3/(mm×mm×mm)3300304542004500×1240×1340

振动传感器布置在左右轴承座，从水平和垂直两个方向测量大端和小端瓦振；在大端和小端都安装了支架固定电涡流传感器用来测量轴的振动；光电传感器安装于转鼓大端。传感器的布置如图8所示。

试验中，测量瓦振的传感器为本特利9200速度传感器，灵敏度为20 mV/(mm/s)；测量轴振的传感器为东南仪器厂生产的电涡流传感器，灵敏度为8 V/mm；测量脉冲信号的传感器为东南仪器厂生产的光电传感器，转速测量取值以脉冲前沿为触发参考。

取大端垂直方向轴振工作阶段的振动信号为例，采样频率为12.8 kHz，采样时间为20 s，图9为其时域信号。

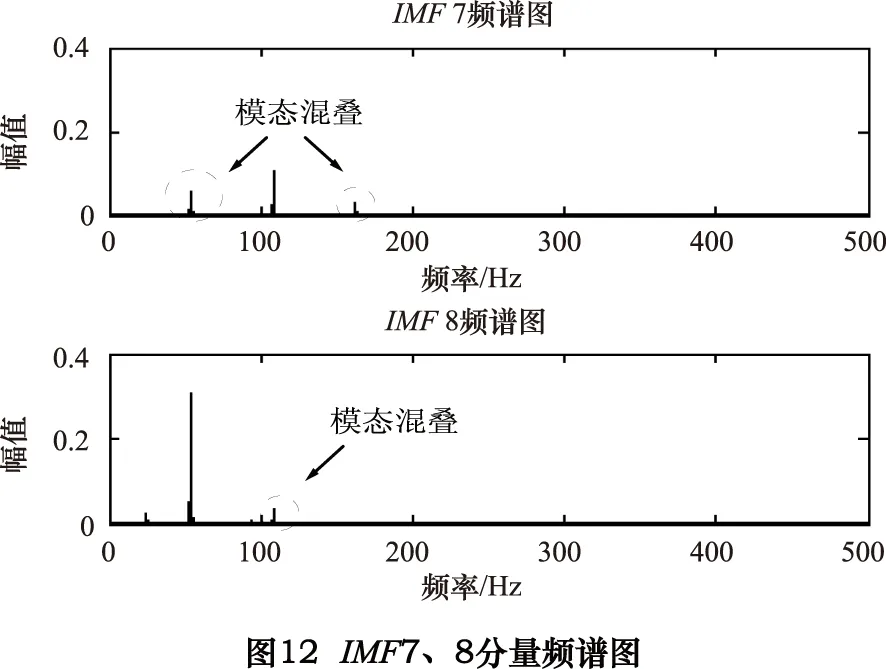
图10看出振动信号由多个频率成分组成，使用解相关CEEMD算法对卧螺离心机的工作频率即55 Hz进行提取。经过文章第2部分算法的1～4步骤，选择分解重复步骤次数n为100，添加的白噪声的幅值标准差为振动信号的0.1倍。由于CEEMD自适应分解后的IMF分量是根据频率段从高到低依次排列下来，因篇幅限制只列出CEEMD分解后特征频率信号所在的、出现模态混叠的IMF7、IMF8两个分量，其时域图和频谱图分别为图11、12。

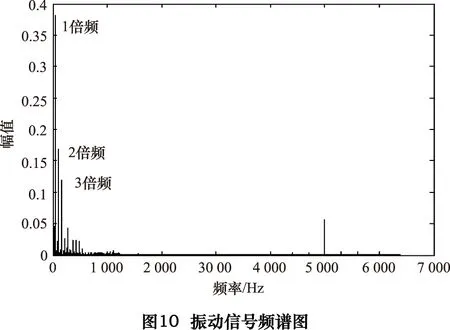
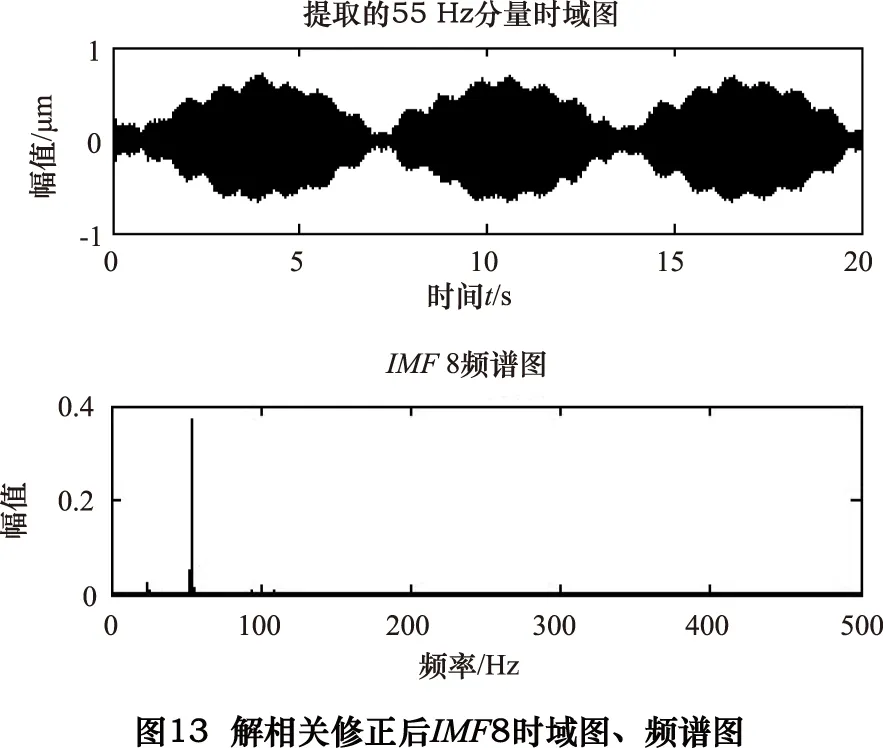
由图12频谱图可知CEEMD自适应分解后，在低频部分依然出现了少量的模态混叠(图中虚线圆圈标注)，特征频率信号55 Hz被分解到IMF7与IMF8内，两者的相关系数λ为26.91%。为了对工作频率信号进行精确提取，故对IMF7和IMF8做解相关修正，设定阈值λ=0.05，解相关修正后提取的工作频率信号如图13所示。

由图13解相关修正后的频谱图可以看出IMF8中1倍频被很好地提取出来，与采集得到的振动信号频谱图进行对比，解相关CEEMD有效地解决了CEEMD分解后依然存在的模态混叠问题，两个模态混叠的IMF分量相关性系数达到阈值以下，实现了对特征频率成分的有效提取。

4 结语

(1)本文介绍了近年来HHT的发展以及在故障诊断中的运用，详细阐述了HHT中EMD信号处理方法的优点以及缺陷，针对EMD的模态混叠问题引入CEEMD。

(2)CEEMD自适应分解虽有效地改善了EMD在含有间断点信号中的模态混叠问题，但在实际应用中低频部分依然存在少量的频率混叠，针对此问题再次结合解相关运算请予以修正，有效地解决了分解后存在的模态混叠问题，实现对特征频率的提取。

(3)运用解相关CEEMD算法对实际工程信号中的特征频率分量进行了精确的提取。

[1]Huang N E, Shen Z, Long S.The empirical Mode decomposition method and the Hilbert spectrum for non-stationary time series analysis [J].Proceedings of the Royal Society, 1998(454): 903-995.

[2]杨宇, 于德介, 程军圣.基于EMD与神经网络的滚动轴承故障诊断方法[J].振动与冲击, 2005, 24(1): 85-88.

[3]陈建国, 张志新, 郭正刚.独立分量分析方法在经验模态分解中的应用[J].振动与冲击, 2009, 28 (1) :109-111.

[4]肖瑛, 殷福亮.解相关EMD:消除模态混叠的新方法[J].振动与冲击, 2015, 34(4):25-29.

[5]Wu Z H, Huang N E.Ensemble empirical mode Decomposition: A noise assisted data analysis method[J].Advances in Adaptive Data Analysis, 2009, 1: 1-41.

[6]雷亚国, 孔德同, 李乃鹏.自适应总体平均经验模式分解及其在行星齿轮箱故障检测中的应用[J].机械工程学报, 2014, 50(3): 64-70.

[7]Yeh J R, Shieh J S.Complementary ensemble empirical mode decomposition: A noise enhanced data analysis method[J].Advances in Adaptive Data Analysis, 2010, 2(2) : 135-156.

[8]Huang N E, Shen S S.Hilbert-Huang transform and its applications[M].Singapore: World Scientific Publishing Copteltd, 2014, 3(1): 22-24.

[9]郑近德, 程军圣, 杨宇.改进的EEMD算法及其应用研究[J].振动与冲击, 2013, 21(32): 45-48.

[10]赵晓平, 侯荣涛.基于Viterbi算法的Gabor阶比跟踪技术[J].机械工程学报, 2009, 45(11): 247-252.

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Research on feature extraction of rolling bearing based on decorrelation CEEMD

ZHANG Yonghong, TAO Runzhe, WANG Lihua, XIE Yangyang

(School of Information and Control, Nanjing University of Information Science & Technology, Nanjing 210044, CHN)

In recent years, along with the time-frequency analysis method of Hilbert Huang transform (HHT) is proposed, the Empirical Mode Decomposition (EMD) has been applied in the rolling bearing fault diagnosis.But whether EMD or its improved Complementary Ensemble Empirical Mode Decomposition (CEEMD), so far mode mixing phenomenon still exists.In order to realize the accurate diagnosis of rolling bearing defection, The need for decomposition of the mode mixing part is corrected, to ensure the Intrinsic Mode Function(IMF) components are not mutually coupled (orthogonal), in order to solve this problem this paper proposes to Decorrelation CEEMD.First, the method applies CEEMD adaptive ability to decompose signals for the extraction of detail, and then the small amount of frequency aliasing exists after decomposition using Decorrelation to modify the part again and the characteristic frequency of signal was extracted.Both simulations and a case of the working frequency of extraction demonstrate that the proposed method is effective.

mode mixing; complementary ensemble empirical mode decomposition; decorrelation; feature extraction

* 国家自然科学基金资助项目( 51405241，51505234，51575283)

TN911.72

B

10.19287/j.cnki.1005-2402.2016.11.015

张永宏，男，1974年生，教授，博士研究生导师，主要研究领域为机械故障无损检测，模式识别与智能系统、气象装备自动化与机电一体化系统集成。

(编辑 孙德茂)

2016-07-12)

161122