偏转板射流式伺服阀前置级液动力计算方法研究

延皓，康硕，王凤聚，李长春，黄静

（北京交通大学机械与电子控制工程学院，北京100044）

偏转板射流式伺服阀前置级液动力计算方法研究

延皓，康硕，王凤聚，李长春，黄静

（北京交通大学机械与电子控制工程学院，北京100044）

针对偏转板射流式伺服阀前置级液动力的计算与检测问题，提出了基于矩形喷口和接收器的前置级节流模型，推导得出了液动力简化计算公式。从射流角度出发，建立了伺服阀前置级的二维流场模型，提出了两种基于仿真离散数据的稳态液动力的计算方法，即动量定理法和压力差法，进行了某型伺服阀的液动力计算。设计了前置级液动力的自动化测试系统，实现了对液动力的测量。仿真与试验表明，理论公式、基于离散数据的数值计算以及试验结果基本一致，从而为此类伺服阀的开发与优化提供了可行的方法和技术。

流体传动与控制；偏转板射流式伺服阀；前置级液动力；节流模型；流场仿真；测试系统

0 引言

偏转板射流式伺服阀，由力矩马达、偏转板射流前置级、功率滑阀三部分组成，是由射流管伺服阀发展演变而来的［1-2］。偏转板射流伺服阀多应用于高可靠性、高温及高压场合下，在军工和工业上均有广泛的用途。

相对于国内外对滑阀与喷嘴挡板阀液动力特性长期大量的研究，目前对于偏转射流伺服阀的液动力特性，尚没有可供借鉴的成熟理论，无法进行精确的理论分析计算。杨月花对不同几何形状接收口的前置级流场分布进行了分析［3］，并根据可视化实验结果对流场分布情况进行了比对；王传礼等［4］提出了偏转板线性化流量方程，并对阀的动态特性进行了仿真验证；訚耀保等推导得出了接收口、供油压力等因素对压力特性的影响规律［5-6］，并基于数值模拟结果，分析了入口压力、接收器恢复压力以及两接收器通道夹角等参数变化对伺服阀前置级流场特性的影响［7］；SHANG等［8］优化了射流盘接收器入口宽度、射流盘厚度等关键参数，以改善偏导阀稳态性能。综上所述，目前关于偏转板射流式伺服阀的研究相对较少，主要是流场与整阀动态特性的分析，对射流喷口和接收口均假设为圆形而与实际元件不符，同时缺乏对前置级液动力的建模分析，也没有给出针对此类阀前置级液动力特性的可行测试方案［9］。

本文以某型偏转板射流式力反馈两级伺服阀为研究对象，提出了基于矩形喷口和接收口的前置级的节流模型，得出了液动力的近似计算公式；并对前置级液动力作用下的射流流场进行了二维建模，提出了动量定理法和压力差法，计算了不同工况下的液动力值和压力特性；同时，设计了专用的自动化测试系统，实现了前置级液动力的测试。

1 偏转板射流式伺服阀前置级建模

偏转板射流式伺服阀由力矩马达、偏转板、射流盘、滑阀、反馈杆组成，结构如图1所示。

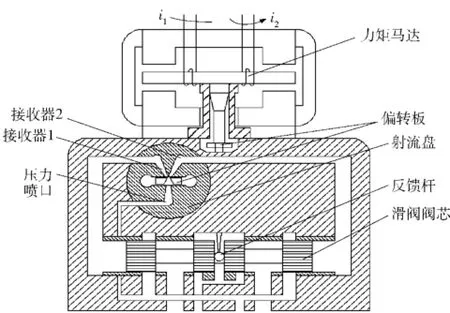
图1 偏转板射流式伺服阀结构原理图Fig.1 Structure diagram of jet deflector servo valve

伺服阀前置级的核心部分为射流盘和偏转板，二者位置关系如图2所示。偏流板在射流盘中沿x轴方向的运动为主要偏移方向。

图2 前置级偏转板偏移示意图Fig.2 Schematic diagram of pilot stage deflection offsets

假定阀匹配对称，阀口处流动为紊流，供油压力恒定，温度和密度均为常数且不考虑管道动态损失，其流量方程为

式中:Cd为流量系数；A3（xf）、A4（xf）、A5（xf）、A6（xf）分别为射流盘两接收口处的各节流面积；Q3、Q4、Q5、Q6分别为通过各节流口的流量；p3、p4分别是射流盘两接收口内压力，如图3所示。

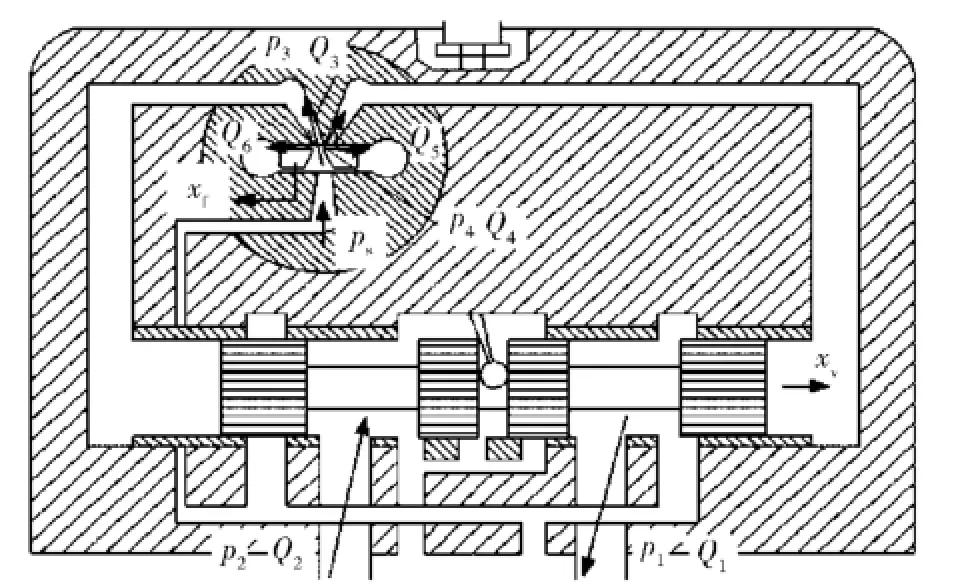
图3 偏转板射流式前置级液流示意图Fig.3 Schematic diagram of pilot stage flow in jet deflector

根据偏转板射流阀前置级的实际结构，有偏转板射流出口与射流盘两接收口的相对位置截面，如图4所示。

图4中，b、c分别为射流盘两接收口长度与宽度，e为两接收口之间距离，B为偏转板射流口宽度，xf为偏转板偏转位移；QL为负载流量。根据几何关系，各节流口面积表达式为

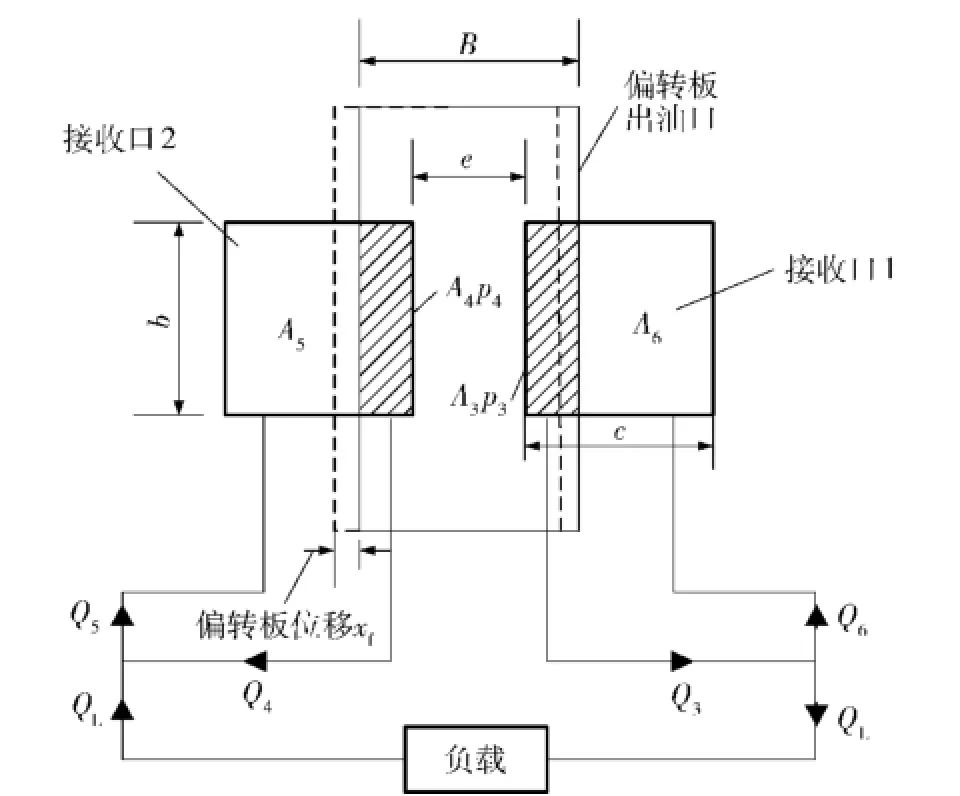
图4 偏转板射流式伺服阀前置级过流面积示意图Fig.4 Schematic diagram of flow area in jet deflector pilot stage

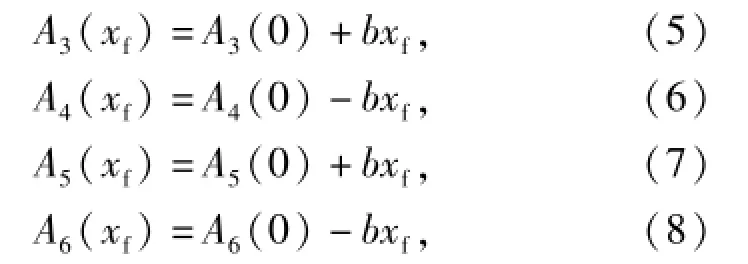
式中:A3（0）、A4（0）、A5（0）、A6（0）为偏转板中位时各节流口的面积。偏转板中位时各节流口的初始面积计算为

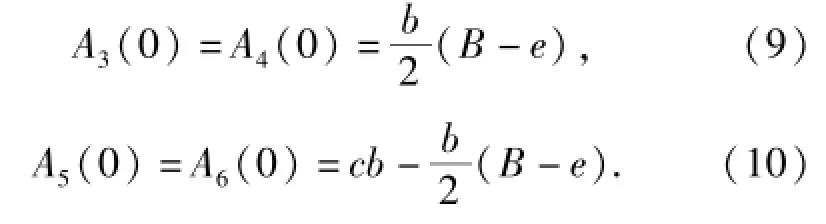
将（9）式与（10）式代入（5）式～（8）式中，得到各节流口面积关于偏转板位移xf的表达式为

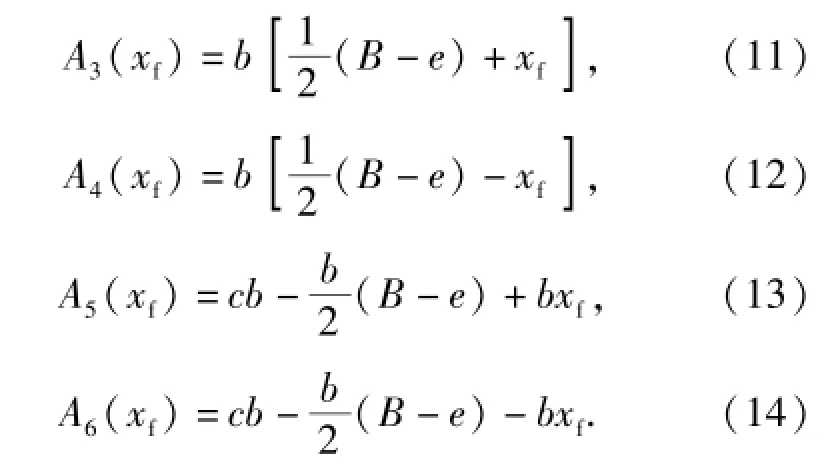
由（11）式和（12）式可知，当接收口和压力喷口机械参数确定时，A3（xf）、A4（xf）可由偏转板位移xf线性表示，且A3与A4面积变化范围为0～Bb.将（11）式和（12）式代入到（1）式、（2）式中，可得到

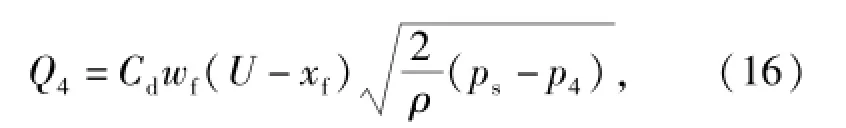
分析系统处于平衡状态时的前置级稳态液动力作用情况，如图5所示。在控制面内对液流应用动量定理，则偏转板对液流的作用力可表示为

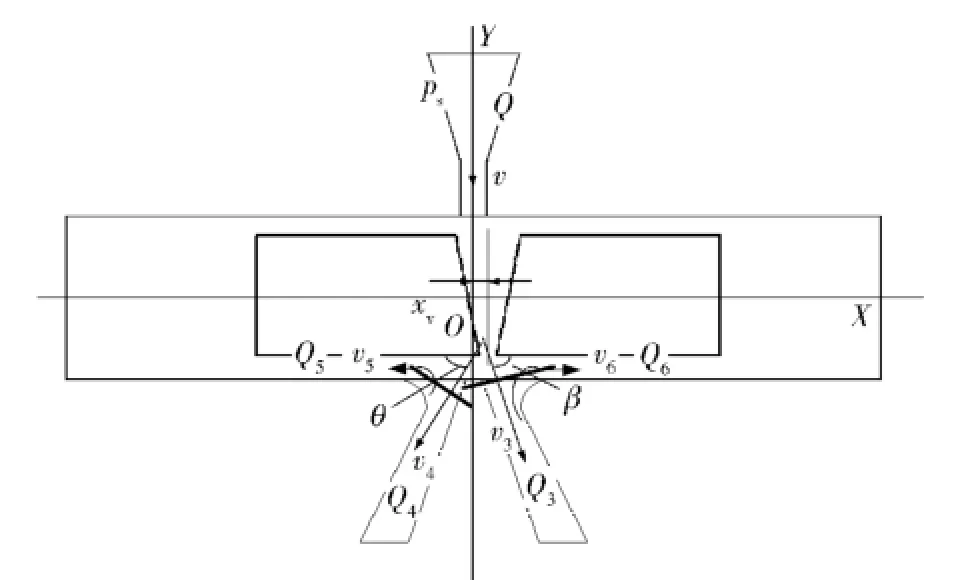
图5 前置级液动力分析图Fig.5 Chart of fluid force in jet deflector pilot stage

由于液动力为反作用力，故有X轴方向与Y轴方向的分力为

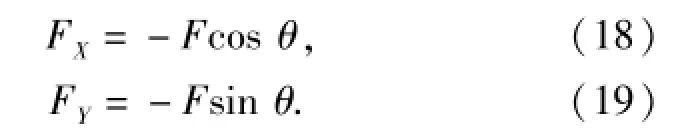
由图2所示，Y轴方向为偏转板的次要运动方向，故忽略该向分力的影响。分析X轴方向的液动力，如图5所示，假设流经偏转板的液流呈现简单的流动形式，则有射流盘处液流对偏转板的X方向液动力为

式中:v为通过喷射口的平均流速；Q、Q3、Q4、Q5、Q6为通过各节流断面的流量；v3、v4为通过两个接收口断面的液流各自的平均流速；θ为液流通过左侧接收口断面处的射角；β为液流通过右侧接收口处射角。由Qi=Aivi，有

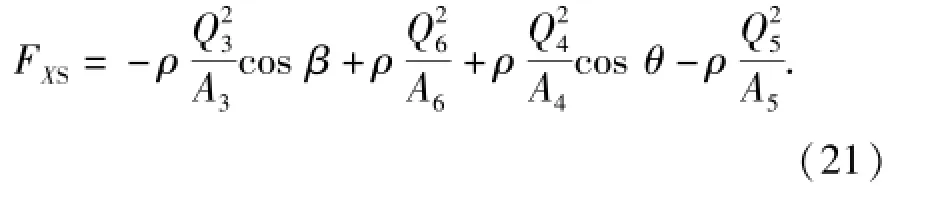
进一步简化，假设偏导板在中位附近小范围工作，则A5≈A6，cos θ≈cos β，由（3）式、（4）式、（15）式和（16）式即可推导得出

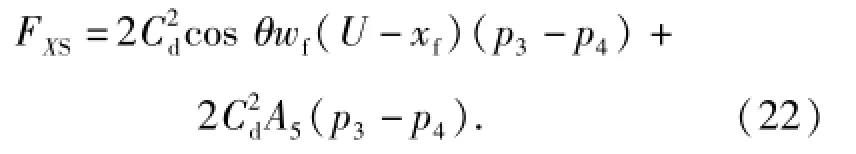
（22）式即为基于动量定理的液动力理论近似计算公式。由（22）式可知，前置级液动力为关于液流出射角、射流盘压力喷口尺寸、接收口尺寸、两接收口距离、接收口压力差以及偏转板位移的函数。上述结论为后续基于数值模拟仿真数据的液动力计算方法的提出提供了理论支撑。

2 基于流场网格离散数据的液动力计算

2.1 偏转射流前置级流场数值模拟

以某型偏转射流力反馈伺服阀的偏转板及射流盘为原型，机械尺寸图如图6所示。

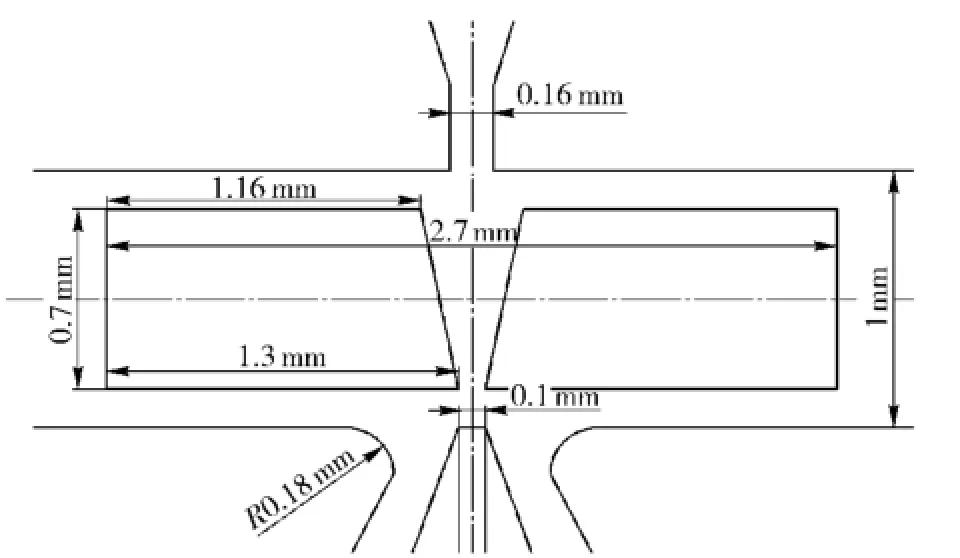
图6 某型射流盘机械尺寸图Fig.6 Dimensions of jet deflector valve pilot stage

由于射流盘为一薄片，平均厚度仅为0.6 mm，整个射流过程只发生在射流盘的薄层片状结构内，故可近似看作平面射流运动。基于此，考虑对前置级流场进行二维建模。在Gambit中建立偏转板偏移量分别为0～0.12 mm等间隔共8种工况，建立二维网格模型。

为保证粘性流体的模拟精度，尽量采用结构化网格对前置级流体部分进行划分。由于偏转板导流槽内部及射流盘接收口处存在能量转化，故须对此处的网格进行加密处理，且须保证沿控制体各边界处的网格均被划分为与该边界平行的正方形。其他部分的网格则可粗略划分。得到0.02 mm偏移时的网格划分结果如图7所示。

在Fluent中进行流场仿真。采用湍流连续性方程、雷诺方程［10］及湍流标准k-ε模型［11］构成封闭方程，建立偏转射流前置级的流场模型，采用SIMPLE算法，求解解耦后的Navier-Stokes方程，动量方程采用1阶迎风格式求解。

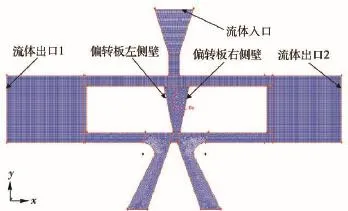
图7 某型偏导阀前置级的网格划分Fig.7 Mesh of jet deflector valve pilot stage

2.2 偏转射流前置级液动力计算方法

2.2.1 前置级液动力动量定理计算法

如图8所示，选取由边界9、边界10、偏转板左侧壁以及右侧壁组成的封闭控制体CV作为研究对象。上边界9和下边界10处有液流进出，左、右侧壁边界处无液流进出。

图8 前置级控制体及液流进出示意图Fig.8 Schematic diagram of flows and control volume in pilot stage

由Fluent数值模拟得到偏转板中位时边界9和边界10处的绝对速度散点图如图9所示。

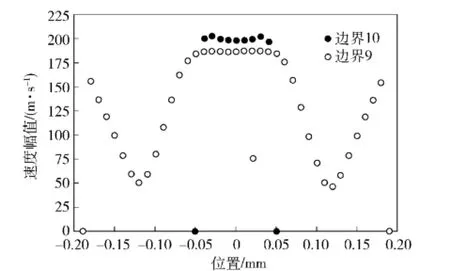
图9 边界9和边界10的绝对速度散点图Fig.9 Velocity magnitude scatter diagram of lines 9 and 10

由于网格划分的离散计算性质，可从仿真数据中获得边界9和边界10处各离散点的液流速度矢量，再根据动量定理，可推得x方向液动力的表达式［12］为式中:vx和vy分别为通过边界9和边界10进出的液流速度在x轴和y轴上的分量绝对值；Ai和Aj分别为沿边界9、边界10的网格平均面积；N1为上边界9、下边界10处沿射流盘厚度方向上的网格个数。

由于采用结构化网格对控制体进行了均匀划分，故沿控制体各边界处的网格均可看作面积相等的小正方形，即Ai=Aj=A，故（23）式可改写为

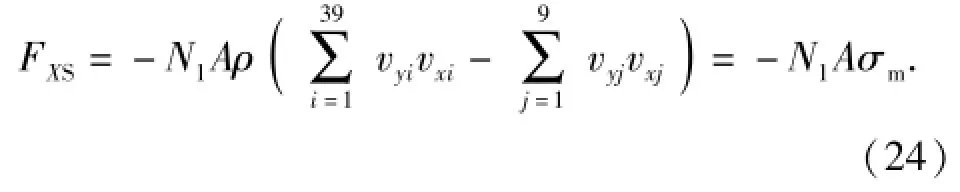
这样，可以定义σm为动量守恒意义下的广义液动应力，N1A为受到液动力作用的广义面积，负号表示液动力阻碍偏转板的位移。

2.2.2 前置级液动力压力差计算法

对射流盘导流槽两斜边的静态压力场进行仿真，得到偏转板偏移时的压力场散点图，如图10所示。

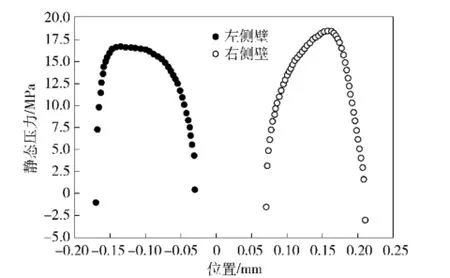
图10 偏转板偏移时两斜边静态压力场散点图Fig.10 Static pressure scatter diagram of two bevel edges with offset

液流在射流盘内部产生的横向稳态液动力为偏转板导流槽左、右侧壁分别所受的液流压力的矢量和。通过仿真获取斜边边界处各离散点的压力数据，分别与其法向网格面积相乘并累加，即可计算出横向稳态液动力，计算公式可表示为

式中:Am和An分别为沿左、右侧壁边界的网格平均面积；Prm和Pln分别为沿偏转板左侧壁和右侧壁边界每个网格对应的离散压力值；N2为两侧边界沿射流盘厚度方向上的网格个数。

同理，考虑沿边界处的网格均匀划分，则有Am=An=A，（25）式可改写为

式中:定义σp为压强意义下的广义液动应力；N2A为广义受力面积。

上述所提出的两种方法结合了Fluent和Gambit的离散计算特性和导出数据功能，均可用于稳态液动力的求解。下面基于此对不同偏移、不同供油压力等条件下的偏转板液动力进行仿真计算。

2.3 前置级液动力仿真计算结果分析

在Fluent中设置如下参数:油液密度849 kg/m3，运动粘度为0.008 49 kg/（m·s），其余参数默认，网格平均面积为A=6.6×10-9m2.

仿真入口处压强分别为21 MPa、19 MPa、17 MPa、15 MPa时不同偏移的液流速度及压力。21 MPa时的速度矢量图如图11所示。

图11 21 MPa下不同偏移时的液流速度矢量图Fig.11 Velocity vector fields at different offsets of 21 MPa

将不同供油压力下的边界9和边界10离散速度矢量，以及偏转板导流槽左、右侧壁边界处离散静态压力值写入data文件。根据2.2节中提出的两种液动力计算方法，分别进行如下具体仿真计算。

2.3.1 动量定理法计算结果

利用由Fluent导出的data数据文件，可获得边界9和边界10处各点得离散速度矢量值，由（24）式计算出偏转板在不同偏移量和不同入口压力下的前置级横向稳态液动力值，统计结果如表1所示。

表1 前置级横向稳态液动力统计（动量定理法）Tab.1 The statistics of lateral steady-state fluid force using momentum theoremN

由动量定理法计算的稳态液动力曲线如图12所示。

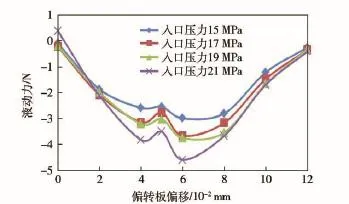
图12 动量定理横向稳态液动力图Fig.12 Lateral steady-state fluid force graph with the momentum theorem

由图12可知，液流在控制体射流和出流的方向始终变化。偏移量一定时，入口压力越大，稳态液动力越大。入口压力一定时，随偏转板向右偏移距离的增大，稳态液动力大小整体呈现先逐渐增加、后逐渐减小的趋势，且始终阻碍偏转板偏移作用。

2.3.2 压力差法计算结果

根据仿真导出的data数据文件中的偏转板导流槽左、右侧壁边界处各点静态压力的离散值，由（26）式可计算出不同偏移和不同压力下的前置级横向稳态液动力值，统计结果如表2所示。

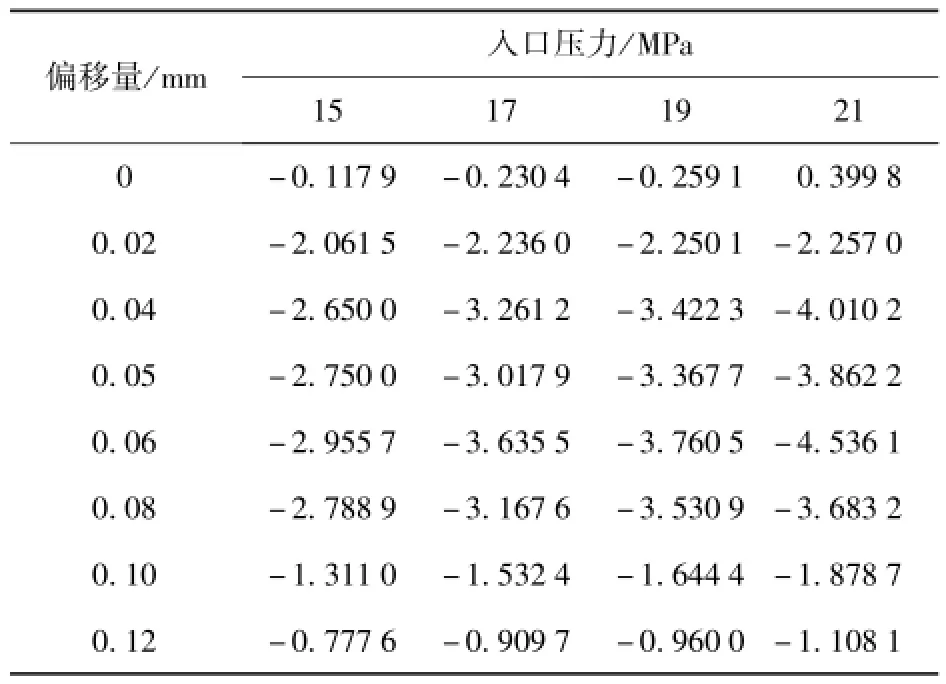
表2 前置级横向稳态液动力统计（压力差法）Tab.2 The statistics of lateral steady-state fluid force using differential pressure methodN

由压力差法计算的稳态液动力曲线如图13所示。

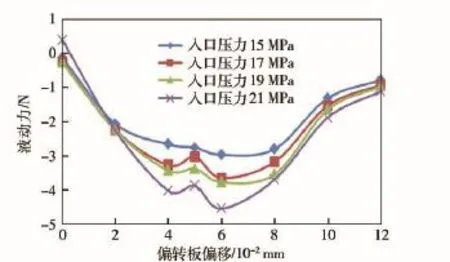
图13 压力差法下稳态液动力图Fig.13 Lateral steady-state fluid force graph using differential pressure method

2.3.3 液动力计算结果对比分析

表3为上述两种方法对液动力计算结果的对比。

由表3可知:当偏移量达到极端位置0.12 mm时，采用上述两种方法分别计算得出的稳态液动力值存在较大误差；而当偏移量处于0～0.1 mm范围内时，两种算法得出的计算结果则基本一致。而实际中，前置级通常在零位附近工作，偏移范围处于0～0.05 mm内，故上述两种方法计算得到的液动力值得到相互印证，并具有实际意义。

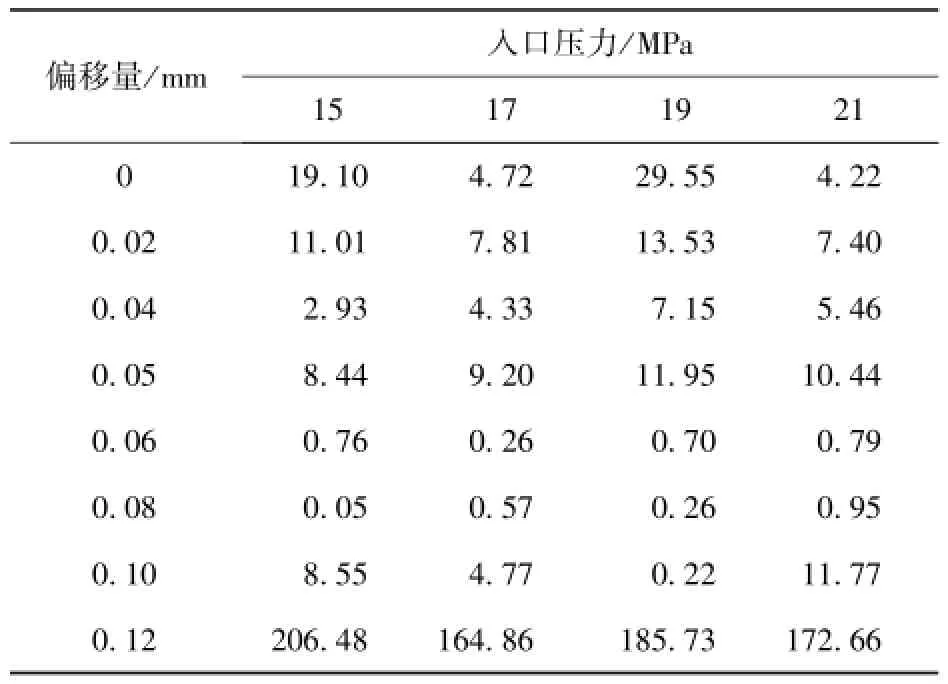
表3 两种方法计算结果的相对偏差Tab.3 Relative errors of steady-state fluid force%

当前置级在零位附近工作时，试验表明两接收口压力差通常与偏转板偏移量呈线性关系，可记为p3-p4=K1xf，K1为压力增益系数。结合第1节中（22）式则可得出如下结论:液动力是关于偏转板偏移量的二次函数。

由此可见，该结论与采用基于仿真离散数据的压力差法与动量定理法获得的液动力曲线一致，证明了基于矩形喷口和接收口节流特性推导的液动力近似计算公式与仿真结果的一致性。

3 液动力测试试验设计与结果分析

3.1 前置级液动力测试方案设计

伺服阀前置级液动力测试系统主要由测试试验台、测试集成模块、伺服阀试验件、计算机测控及数据分析系统四部分组成，如图14所示。

图14 前置级液动力测试系统组成Fig.14 Composition of test system for fluid force in pilot stage

在测试试验台的装置中，施力推杆相互垂直的对位安装于伺服阀衔铁上方的测试工装中，可在两个方向上实现恒力推动，如图15所示。

在试验过程中，主控制器通过推杆对衔铁组件施加角度偏转信号，同时利用激光传感器以及微力传感器检测测试工装的加工块偏移量与偏移回复力，构成精确的位置闭环系统；亦可以通过数字模拟转换卡，直接对伺服阀线圈输入控制电流，实现对伺服阀的控制。测试系统原理如图16所示。

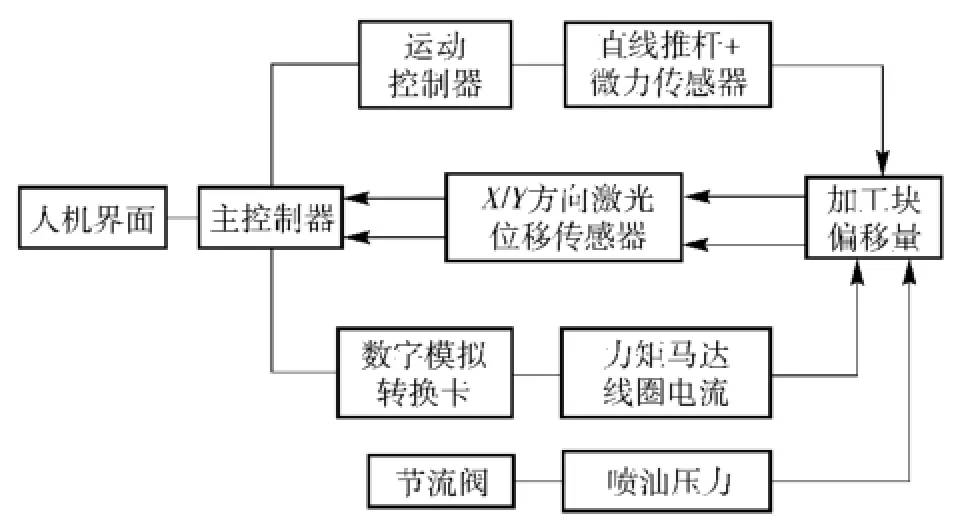
图16 前置级液动力测试系统原理图Fig.16 Schematic diagram of test system for fluid force in pilot stage

当力传感器检测力值时，通过两个激光传感器测量同一水平面内横向与纵向上的力矩马达偏转位移，获取偏转位移-力矩马达负载力值曲线，通过是否通油的对比试验，能够得到液动力-位移曲线。

3.2 试验结果与分析

入口压力分别设置为15 MPa、17 MPa、19 MPa以及21 MPa，偏转板偏移范围为0～0.05 mm，偏移量逐渐增大，得到不同工况下的随偏转板位置偏移的液动力变化曲线如图17所示。

由图17可知，当入口压力一定，偏转板在0～0.05 mm范围内偏移时，液动力随偏移量增加而增大；当偏移量一定时，随着入口压力的逐渐增大，液动力也呈增大趋势。试验曲线所描述的液动力上升段，与理论计算及数值仿真曲线基本一致，证明了理论计算与基于数值模拟计算方法的可行性。而在零位附近，试验曲线更接近于线性，与理论推导和数值模拟有所不同，应与阀口加工精度有关，有待进一步分析研究。

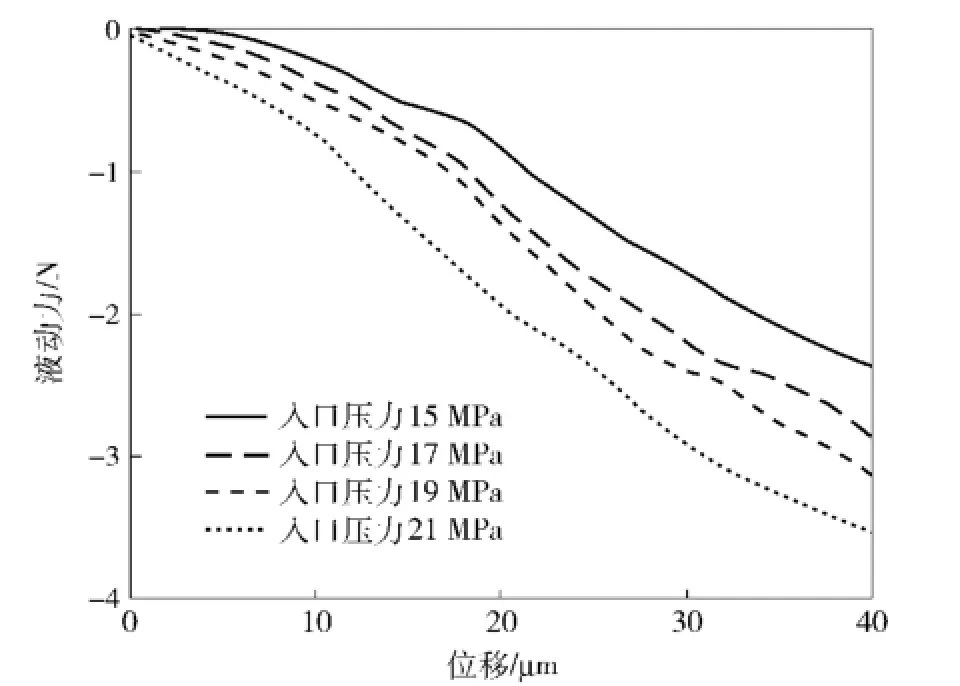
图17 偏转板位移与前置级液动力曲线Fig.17 Pilot stage offset vs.steady-state fluid force

4 结论

1）伺服阀前置级结构复杂，通过与实际更一致的矩形喷口和接受口建模和液动力公式推导，确定液动力的大小与液流出射角、喷口尺寸、接收口尺寸、两接收口距离、接收口压力差等参数的函数关系，为设计新型号力矩马达和前置级的设计提供了理论支持。

2）利用有限体积法的基本思想，构建了两种基于结构化映射网格的液动力计算方法。数值计算、液动力理论公式和试验曲线得到了相互印证，证实了此类方法的可行性。

3）所提出的液动力测试方案能够间接测得前置级液动力值，且与仿真计算结果基本一致，证明了该方案的可行性。同时通过试验发现，零位附近的液动力存在近似线性的现象。

4）本文的研究结果对偏导类伺服阀前置级液动力模型建立以及测试系统的设计具有指导意义或参考价值。

（References）

［1］ 卢长耿，李金良.液压控制系统的分析与设计［M］.北京:煤炭工业出版社，1992. LU Chang-geng，LI Jin-liang.Analysis and design of hydraulic control system［M］.Beijing:China Coal Industry Publishing House，1992.（in Chinese）

［2］ 方群，黄增.电液伺服阀的发展历史、研究现状及发展趋势［J］.机床与液压，2007，35（11）:162-164. FANG Qun，HUANG Zeng.Developing process，research actuality and trend of electrohydraulic servovalve［J］.Machine Tool& Hydraulics，2007，35（11）:162-164.（in Chinese）

［3］ 杨月花.伺服阀前置级射流流场分析及实验研究［D］.哈尔滨:哈尔滨工业大学，2006. YANG Yue-hua.Analysis and experimental research of prestage jet flow field in hydraulic servo valve［D］.Harbin:Harbin Institute of Technology，2006.（in Chinese）

［4］ 王传礼，丁凡，李其朋，等.射流盘伺服阀控电液位置系统的动态特性［J］.重庆大学学报，2003，26（11）:11-15. WANG Chuan-li，DING Fan，LI Qi-peng，et al.Dynamic characteristics of electro-hydraulic position system controlled by jet-pan servo valve［J］.Journal of Chongqing University，2003，26（11）: 11-15.（in Chinese）

［5］ 訚耀保，张鹏，张阳.偏转板伺服阀压力特性研究［J］.流体传动与控制，2014，65（4）:10-15. YIN Yao-bao，ZHANG Peng，ZHANG Yang.Analysis of the pressure characteristics of deflector jet servo valve［J］.Fluid Power Transmission and Control，2014，65（4）:10-15.（in Chinese）

［6］ 訚耀保，黄伟达，张曦.电液伺服阀喷嘴挡板阀流场分析［J］.流体传动与控制，2011，46（3）:1-5. YIN Yao-bao，HUANG Wei-da，ZHANG Xi.On the flow field of nozzle flapper valve of electro-hydraulic servo valve［J］.Fluid Power Transmission and Control，2011，46（3）:1-5.（in Chinese）

［7］ 訚耀保，张鹏，岑斌.偏转板射流伺服阀前置级流场分析［J］.中国工程机械学报，2015，13（2）:1-7. YIN Yao-bao，ZHANG Peng，CEN Bin.Prestage flow field analysis on deflector jet servo valves［J］.Chinese Journal of Construction Machinery，2015，13（2）:1-7.（in Chinese）

［8］ Shang Y X，Zhang X S，Hu C W，et al.Optimal design for amplifier of jet deflector servo valve［J］.Hydromechatronics Engingeering，2015，43（3）:11-15.

［9］ 吴鸣嵩.电液流量伺服阀计算机辅助测试系统的研制［D］.南京:南京理工大学，2007. WU Ming-song.Research and design of electro-hydraulic servo valve computer-aided test-bed［D］.Nanjing:Nanjing University of Science and Technology，2007.（in Chinese）

［10］ Smith L M，Woodruffs L.Renormalization-group analysis of turbulence［J］.Annual Review of Fluid Mechanics，1998，30（5）: 275-310.

［11］ Choudhury D，Kim S E，Flannery W S.Calculation of turbulent separated flows using a renormalization group based k-ε turbulence model［J］ASME-PUBLICATIONS-FED，1993，149（6）: 177-177.

［12］ 冀宏，傅新，杨华勇.非全周开口滑阀稳态液动力研究［J］.机械工程学报，2003，39（6）:13-17. JI Hong，FU Xin，YANG Hua-yong.Study on steady flow force of non-circular opening spool valve［J］.Journal of Mechanical Engineering，2003，39（6）:13-17.（in Chinese）

Research on the Calculation Methods of Fluid Force in Pilot Stage of Jet Deflector Servo Valve

YAN Hao，KANG Shuo，WANG Feng-ju，LI Chang-chun，HUANG Jing
（School of Mechanical，Electronic and Control Engineering，Beijing Jiaotong University，Beijing 100044，China）

In order to analyze the fluid force in the pilot stage of jet deflector servo valve，an orifice model based on the rectangular nozzle and receiver of jet plate in pilot stage is established，and a simplified formula of fluid force is obtained.From the perspective of jet flow field，a two-dimensional internal flow field model of jet deflector pilot stage is established.And the momentum theorem method and the differential pressure method are presented to calculate the steady-state fluid force based on the simulated discrete data.An automatic test system for measuring the fluid force in pilot stage is designed.The results show that the calculated results based on simulated discrete data are basically consistent with the theoretically calculated and experimental results.

fluid drive and control；jet deflector servo valve；pilot stage fluid force；orifice model；flow field simulation；test system

TH137.52

A

1000-1093（2016）07-1258-08

10.3969/j.issn.1000-1093.2016.07.014

2015-11-27

国家国际科技合作专项项目（2012DFG71490）

延皓（1979—），男，教授，博士生导师。E-mail:hyan@bjtu.edu.com