基于多层自助最大熵法的可靠性评估

夏新涛，叶亮，李云飞，常振

（河南科技大学机电工程学院，河南洛阳471003）

基于多层自助最大熵法的可靠性评估

夏新涛，叶亮，李云飞，常振

（河南科技大学机电工程学院，河南洛阳471003）

在小样本无任何先验信息的条件下，提出多层自助最大熵评估模型分析机械产品寿命可靠性。用自助法对当前无失效数据样本进行再抽样，获得足够的样本数据。基于最大熵法，改变抽样个数得到不同的拉格朗日乘子。再次运用自助法对拉格朗日乘子的小样本数据进行再抽样，基于最大熵法获得拉格朗日乘子的区间估计。对每个拉格朗日乘子的上下限进行排列组合，得到多个概率密度函数和可靠性函数，运用最小不确定性原理得到可靠性函数的区间估计。试验研究表明，多层自助最大熵评估模型可以有效地解决概率分布已知或未知的小样本无失效数据的可靠性评估问题。

系统评估与可行性分析；可靠性评估；多层自助最大熵法；乏信息；无失效数据；拉格朗日乘子

0 引言

目前，无失效数据的可靠性评估方法主要有经典统计方法和贝叶斯统计方法。经典统计理论认为，通过实验获得的失效数据越多，对产品进行可靠性评估的结果越准确。但是，对于许多高可靠性或危险的试验来说，很难获得失效数据，例如高端武器和航天航空飞行器的试验等。因此，无失效数据的可靠性评估问题日益引起学术界的关注。在机械产品可靠性试验中，获得的数据通常有3类，即失效数据、不完全失效数据、无失效数据。目前，对失效数据的研究已经达到比较高的水平。然而对无失效数据的研究还不够深入，因此这也是长期以来国内外研究的热点与难点。

关于无失效数据的可靠性分析，很多研究工作已经取得了相应的成果。如傅惠民等［1］提出一种Weibull分布定时无失效数据可靠性分析方法，在形状参数下限已知的情况下，给出了可靠度和使用寿命的单侧置信下限，从而能够根据定时无失效数据对产品进行高置信水平的可靠性评定；王凭慧等［2］在高置信水平下提出了一种卫星推力器无失效数据的可靠性分析方法；李宝盛等［3］求出了工作寿命可靠度置信区间的解析公式，计算和分析了不同试验样本工作寿命可靠度的置信限，得出了对可靠性评估有指导意义的结论；蒲星［4］运用Bayes方法对无失效数据问题进行了有效的可靠性研究，分析了无失效数据产生的原因，并提出了运用黄金分割系数求失效概率的方法。但召江等［5］在形状参数先验分布分别为均匀分布与拟合出的概率分布时，利用无失效试验数据得出失效率和形状参数的Bayes估计，进而计算出Weibull分布的特征寿命；Jiang等［6］提出了运用修整极大似然方法估计威布尔分布的参数。在国外，Nam等［7］以深沟球轴承为例，研究了轴承在高温条件下的寿命可靠性；Bailey［8］基于无失效数据，建立了二项概率分布的预测模型；Kwon［9-10］基于Bayes方法，分别针对寿命服从Weibull分布和对数正态分布的产品，提出了无失效数据样本的可靠性验证方法。

对于未知概率分布的小样本数据的可靠性评估问题，现有的可靠性评估方法难以解决，到目前为止还是一个重要的科学技术难题。鉴于此，夏新涛等［11］以灰色系统的基本原理为依据，构建出特殊的灰相似空间，允许概率分布未知和数据个数很少（n≥4）。贾波等［12］在仿真实现过程中，发现最大熵方法存在溢出的问题，通过变量变换法成功解决了此问题。夏新涛等［13］将灰自助原理融入泊松过程，提出灰自助泊松方法，以预测滚动轴承振动性能可靠性的变异过程。基于最大熵法，胡松伟［14］提出了火工品类关键单元可靠性验证的LQB型方案。在国外，Yeom等［15］提出改进的最大熵抽样方法，从而使大多数抽样点落在一个用复杂的非线性函数表示的可行域内；Young等［16］基于最大熵原理，求解第一结尾时间序列的可靠性边界。

根据测量理论和统计理论，任何参数估计都伴随不确定性，可靠性评估中的不确定性可以用可靠性估计区间来表示。现有可靠性理论把拉格朗日乘子当作常数，而Bayes理论认为统计学上的参数可当作变量，可以对参数进行区间估计，因而也能对可靠性函数做出区间估计。因此本文对于只有无失效数据而没有概率分布任何先验信息条件下机械产品的可靠性评估问题，提出了多层自助最大熵评估模型来分析机械产品寿命可靠性。具体过程如下:首先，运用自助法对小数据样本进行等概率可放回再抽样，获得大量样本数据。改变每次抽样个数，基于最大熵法，可得到多个不同的拉格朗日乘子。然后，再次利用自助法对所有的拉格朗日乘子进行再抽样，多次使用最大熵法获得每个拉格朗日乘子的区间估计。最后，对各个拉格朗日乘子的上下限进行排列组合，得到多个概率密度函数和可靠性函数，根据最小不确定性原理获得可靠性函数的区间估计。通过试验证明运用该方法能够对可靠性函数做出合理的区间估计，分析结果真实可信。

1 多层自助最大熵法原理

1.1 自助法原理

假设通过试验获得一组无失效数据序列X，用向量表示为

式中:xl为第l个无失效数据；n为无失效数据的个数。

从无失效数据样本X中等概率可放回地抽样，每次抽取t个数据，连续重复抽取B次，可以得到自助样本Xt为

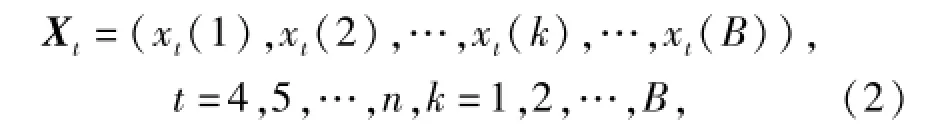
式中:t为每次抽取原始样本数据的个数；k为生成自助样本的数据序号；xt（k）为每次抽取t个数据生成自助样本的第k个数据。

1.2 基于最大熵方法求解概率密度函数

最大熵方法能够对未知的概率分布做出主观偏见为最小的最佳估计。在求解过程中，引入拉格朗日乘子，从而把概率分布问题转化为拉格朗日乘子的求解问题。

为了叙述方便，将离散的无失效数据序列X连续化，定义最大熵的表达式为

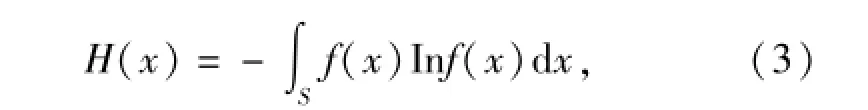
式中:f（x）为连续化后的数据序列的概率密度函数；Inf（x）为概率密度函数的对数；S为积分区间。

通过调整f（x）可以使熵达到最大值，同时采取拉格朗日乘子法求解。设为拉格朗日函数，可得

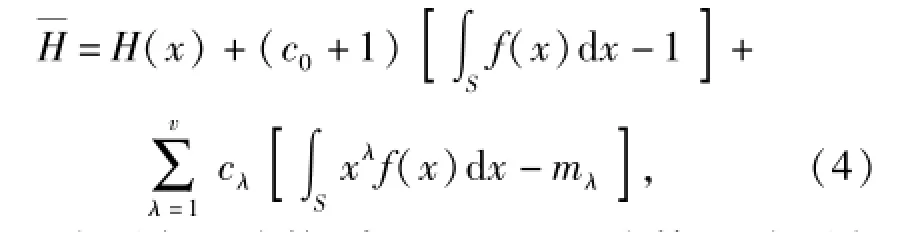
式中:v为原点矩阶数，常用v=5；mλ为第λ阶原点矩；xλ为求解第λ阶原点矩时f（x）的系数；cλ为第λ+1个拉格朗日乘子，λ=0，1，…，v.

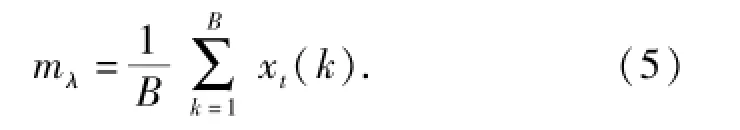
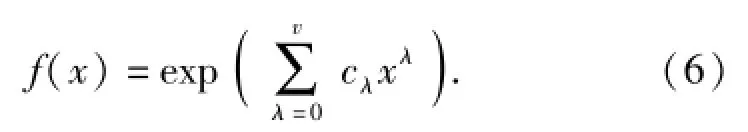
其他m个拉格朗日乘子应满足

1.3 积分区间的映射

为了使求解收敛，将无失效数据按递增的顺序排列并分成j组，画出直方图，同时可得到组中值zq和频数pq，q=2，3，…，j+1.然后将直方图扩展成j+ 2组，并令p1=pj+2.将原始数据区间S映射到区间［-e，e］中，具体如下:

令

式中:a、b为映射参数；w为所要变换的自变量；x∈［-e，e］，

由dx=dw/a可得

因此，最大熵概率分布密度函数由（6）式变换为

1.4 求解概率密度函数的上下限

现有可靠性理论把拉格朗日乘子当做常数，不能获得概率密度函数的上下限。因此，本文根据Bayes原理，把拉格朗日乘子当做变量，运用多层自助最大熵方法求出概率密度函数的上下限。

改变抽样个数k，基于自助最大熵法可得到不同的拉格朗日乘子Cλ和映射参数a、b.

式中:cλ（t）为每次抽取t个数据时的第λ+1个拉格朗日乘子系数；a（t）、b（t）为每次抽取t个数据时的区间映射参数。

1.4.1 各个拉格朗日乘子的区间估计

将各个拉格朗日乘子作为源信息样本，再进行等概率可放回地抽样。基于最大熵方法，可求解得各个拉格朗日乘子的区间估计。

假设显著性水平为α，α∈［0，1］，则置信水平P为

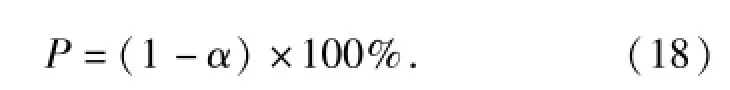
各个拉格朗日乘子cλ在置信水平P下的下边界值设为cλL，则有

式中:cλ0为积分变量初始值。

因此，参数的估计区间为

1.4.2 映射参数的点估计

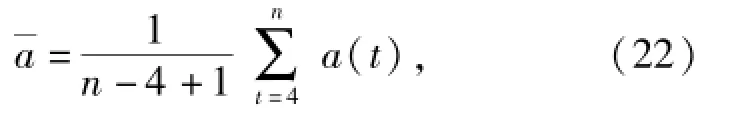
1.4.3 概率密度的上下界函数求解

分别将拉格朗日乘子的上限或下限值，映射参数的点估计值代入（13）式中，由排列组合原理，可得2v+1条概率密度函数曲线的表达式为

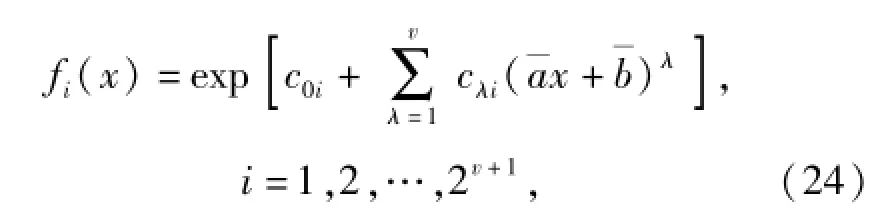
式中:i为概率密度函数的序号；c0i为第i个概率密度函数的第1个拉格朗日系数，c0i=c0L或c0i=c0U；cλi为第i个概率密度函数的第λ+1个拉格朗日系数，cλi=cλL或cλi=cλU，cλU、cλL分别为拉格朗日乘子cλ的上下限。

定义概率密度估计真值函数f0（x）为

式中:f0（x）为每次抽取原始样本数据个数n时的概率密度函数；c00、cλ0分别为每次抽取n个数据时的第1个和第λ+1个拉格朗日系数；a0、b0为每次抽取n个数据时的区间映射参数。

根据最小不确定性原理，可以从概率密度函数曲线中得到距离概率密度估计真值函数f0（x）最近的上下两条曲线，即最大熵概率密度分布的上下界函数fU（x），fL（x）.

1.5 可靠性的上下界函数求解

1.5.1 可靠性估计真值函数

将每次抽取原始无失效数据样本个数n时计算所得的可靠性函数作为其估计真值函数R0（x），具体计算如下:对最大熵概率密度估计真值函数f0（x）积分，得到最大熵概率分布估计真值函数F0（x）为

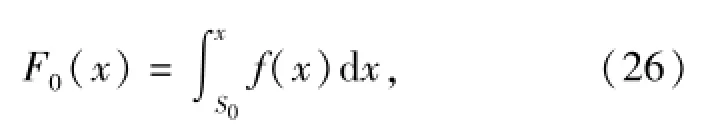
式中:S0为积分区间下限值。

设可靠性系数为rc，由个体无失效数据个数n可得总体的失效概率估计真值函数P0（x）为

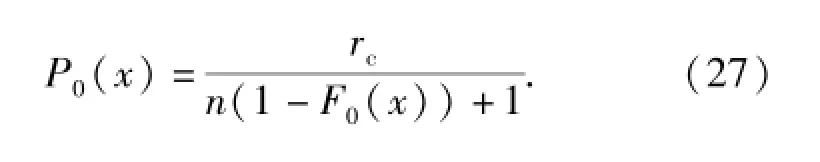
总体可靠性估计真值函数也即最大熵可靠性估计真值函数R0（x）为

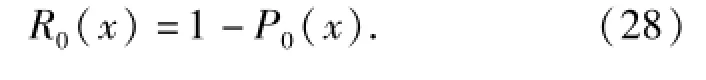
1.5.2 可靠性函数的区间估计

将最大熵概率密度分布的上下界函数fU（x）、fL（x）分别代入式（26）、（27）、（28）中，可求解出可靠性函数的上下界曲线RU（x）、RL（x）为

给定置信水平P，根据可靠性函数的真值估计曲线R0（x），得到估计真值x0.将其代入到可靠性函数的上下限中，计算出可靠性函数的区间估计为

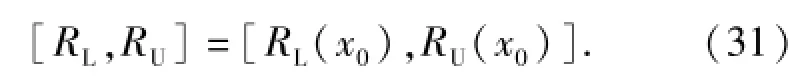
2 试验研究

案例1 根据文献［17］，认为轴承的寿命概率分布为威布尔分布。对20套轴承进行寿命试验，获得的无失效数据如下:

X=（422，422，539，539，539，539，602，602，

770，770，770，770，847，847，847，

847，924，924，924，924）.

用自助法每次抽取20个数据，共抽取30 000次，所得数据如图1所示。

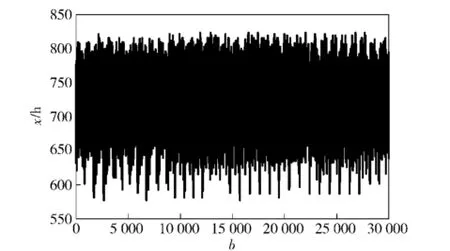
图1 自助法获取轴承样本数据Fig.1 Sample data of bearings obtained by bootstrap method

基于最大熵法计算可得:映射参数a0=0.016 8，b0=-11.974 0；拉格朗日乘子（c00，c10，c20，c30，c40，c50）=（-4.601 9，0.351 5，-1.135 0，-0.022 6，-0.025 2，-0.003 8）.

由（25）式可计算出概率密度估计真值函数f0（x），将f0（x）代入（26）式、（27）式、（28）式中，可得可靠性估计真值函数R0（x），如图2所示。由图2可得:R0（677）=0.994 5，与文献［17］中运用Bayes方法计算出的R（677）=0.9762相差0.0183.这表明自助最大熵方法的可靠性估计真值结果与用Bayes方法的可靠性估计真值结果相差很小。可见自助最大熵方法获得的可靠性估计真值函数的拟合效果跟Bayes方法的估计结果基本一致。但是自助最大熵方法对概率分布没有要求，而且能解决小样本数据的可靠性评估问题。因此，用自助最大熵方法获得的可靠性估计真值函数评估机械产品的可靠性是有效且可行的。

改变每次抽样个数t，共抽取30 000次，可得拉格朗日乘子如表1所示。

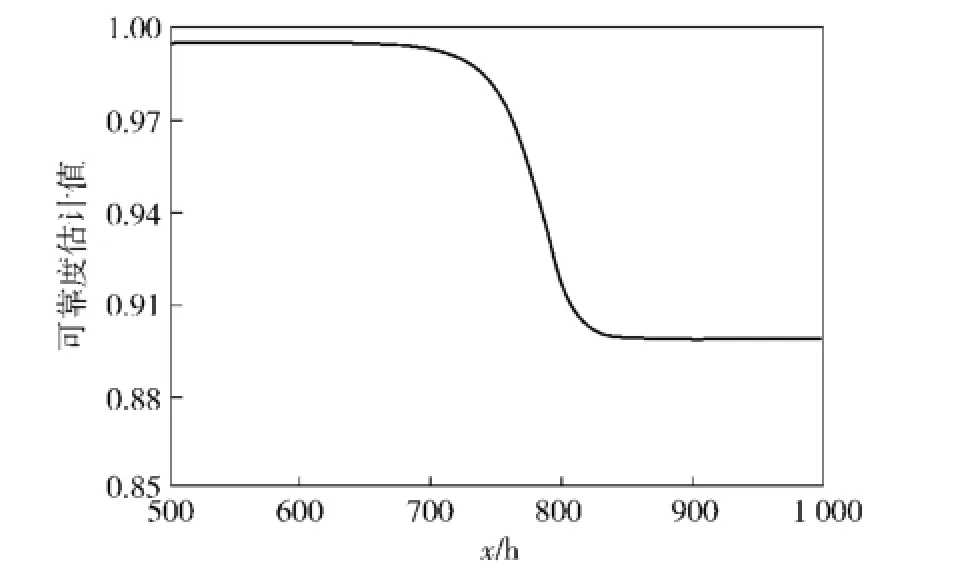
图2 可靠性估计真值函数曲线Fig.2 Estimated true value function curve of reliability

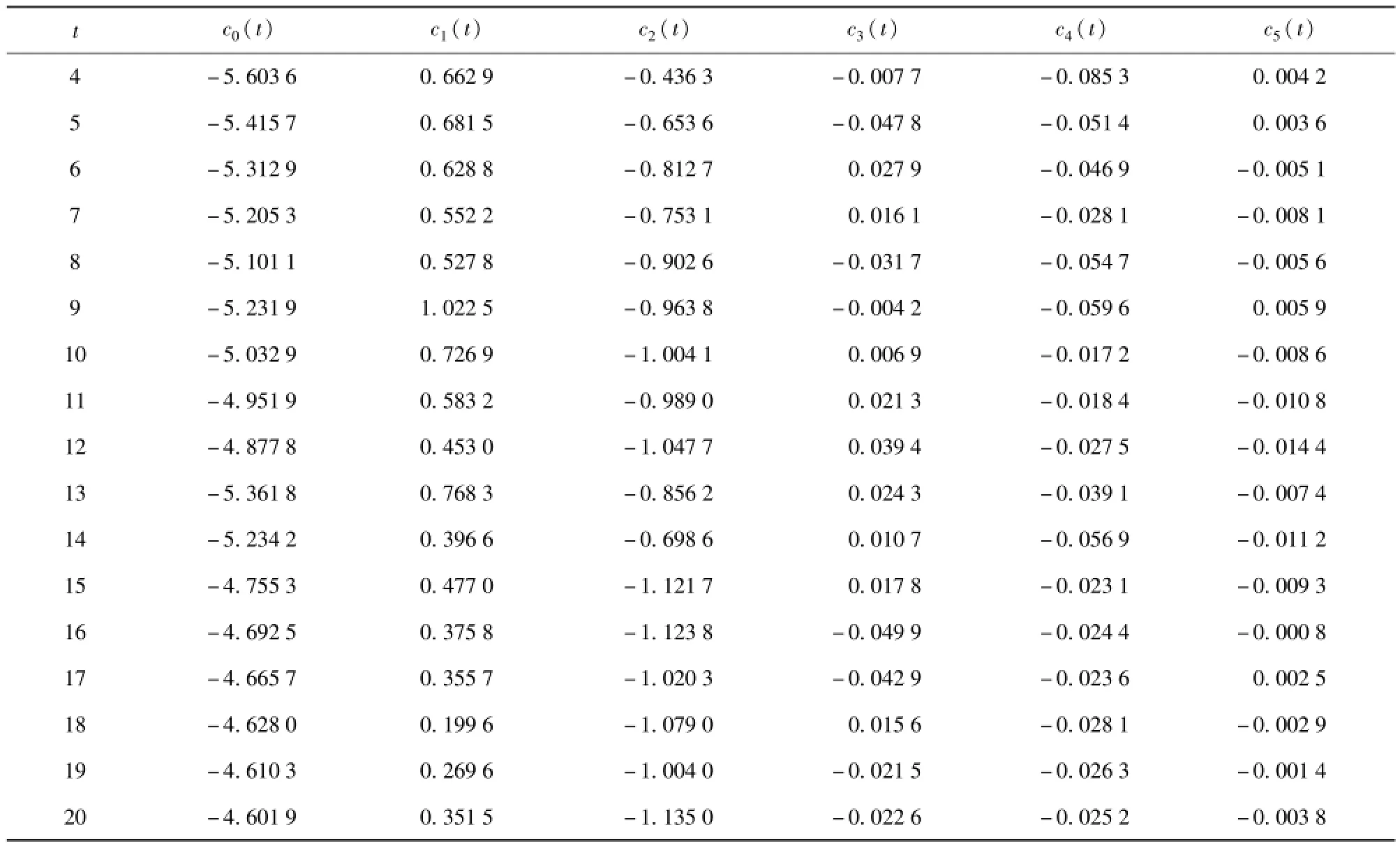
表1 改变抽样个数所得各个拉格朗日乘子Tab.1 Lagrange multipliers obtained by changing the number of samples

设置信水平P=90%，即α=0.10，将所得的17个c0值作为样本进行自助再抽样可得:置信区间的下边界值c0L=-5.156 4；置信区间的上边界值c0U=-4.869 1.

因此，参数c0的估计区间:［c0L，c0U］=［-5.156 4，-4.8691］.

同样算得参数c1的估计区间:［c1L，c1U］=［0.4367，0.634 0］；参数c2的估计区间:［c2L，c2U］=［-1.004 8，-0.842 8］；参数c3的估计区间:［c3L，c3U］=［-0.015 7，0.009 9］；参数c4的估计区间:［c4L，c4U］=［-0.044 1，-0.028 4］；参数c5的估计区间:［c5L，c5U］=［-0.007 6，-0.002 3］.

改变每次抽样个数，共抽取30 000次，可得映射参数如表2所示。

经过计算，参数a、b的估计值分别为

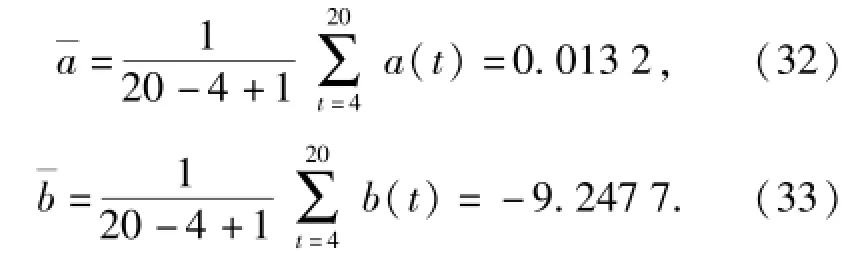
分别将拉格朗日乘子的上限或下限值，映射参数的点估计值代入（24）式中，由排列组合原理和最大熵方法，可得64个概率密度函数。

表2 改变抽样个数所得映射参数Tab.2 Mapping parameters obtained by changing the number of samples

经过计算，由最小不确定性原理可得:当c0= c0L=-5.156 4，c1=c1U=0.634 0，c2=c2U=-0.842 8，c3=c3U=0.009 9，c4=c4U=-0.028 4，c5=c5U= -0.002 3时，可得到可靠性函数的上限曲线RU（x）；当c0=c0U=-4.869 1，c1=c1L=0.436 7，c2=c2L= -1.004 8，c3=c3L=-0.015 7，c4=c4L=-0.044 1，c5=c5L=-0.007 6时，可得到可靠性函数的下限曲线RL（x）.如图3所示。

图3 可靠性函数曲线Fig.3 Curves of reliability functions

由图3可知可靠性函数取值随着自变量时间的增大而逐渐减小，这是符合工程实际的。而且在x= 700 h之前，可靠性函数上下限曲线图均与可靠性估计真值函数曲线图基本完全重合。在x=700 h之后，随着时间的增加，可靠性函数上下限曲线均越来越偏离可靠性估计真值函数曲线。这是因为在当前时间段内，对可靠性函数估计的不确定度较小。随着时间变量的增大，可靠性函数的估计难度逐渐增大，对可靠性函数估计的不确定度也逐渐增大，即上下限值越来越偏离估计真值。

设可靠性系数rc=0.1，置信水平P=90%，即显著性水平α=0.1，计算出估计真值x0:x0=826 h.可靠性函数的区间估计为

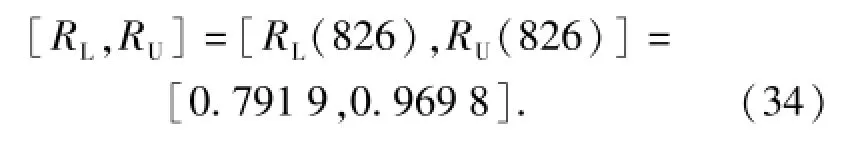
案例2 根据文献［18］，认为导弹寿命的概率分布为指数分布。对19个导弹进行寿命试验，获得的无失效数据如下:

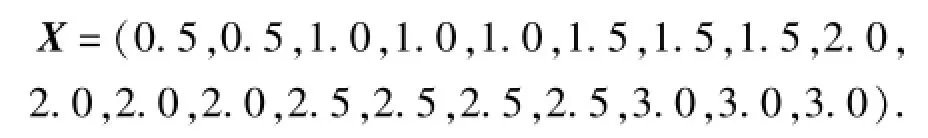
用自助法每次抽取19个数据，共抽取30 000次，所得数据如图4所示。

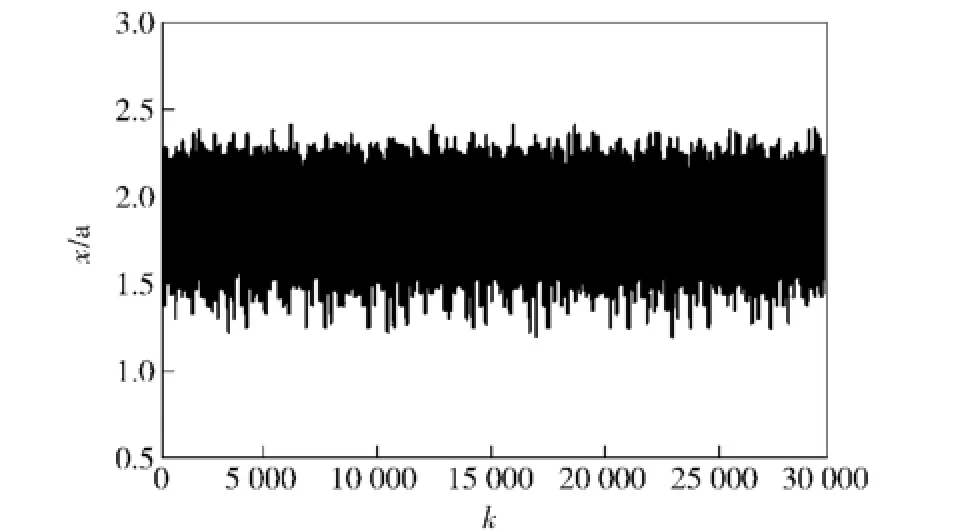
图4 自助法获取导弹样本数据Fig.4 Sample data of missiles obtained by bootstrap method

基于最大熵法计算可得:映射参数a0=3.575 6，b0=-6.774 8.拉格朗日乘子（c00，c10，c20，c30，c40，c50）=（0.730 4，-0.150 8，-0.939 5，0.009 6，-0.103 9，-0.013 1）.

由（25）式可计算出概率密度估计真值函数f0（x），将f0（x）代入（26）式、（27）式、（28）式中，可得可靠性估计真值函数R0（x），如图5所示。

文献［18］中运用Bayes方法计算出R（3）= 0.916 4，运用多层自助最大熵方法计算出的R0（3）=0.898 0，二者相差0.018 4.这表明多层自助最大熵方法的可靠性估计真值结果与用Bayes方法的可靠性估计真值结果误差很小。可见自助最大熵方法获得的可靠性估计真值函数的拟合效果跟Bayes方法的估计结果基本一致。但是自助最大熵方法对概率分布没有要求，而且能解决小样本数据（n=19）的可靠性评估问题。因此，用多层自助最大熵方法评估机械产品的可靠性是有效且可行的。

改变每次抽样个数t，共抽取30 000次，所得拉格朗日乘子如表3所示。

设置信水平P=90%，即α=0.10，将所得的16个c0值作为样本进行自助再抽样可得:置信区间的下边界值c0L=0.359 4，置信区间的上边界值c0U=0.592 4.

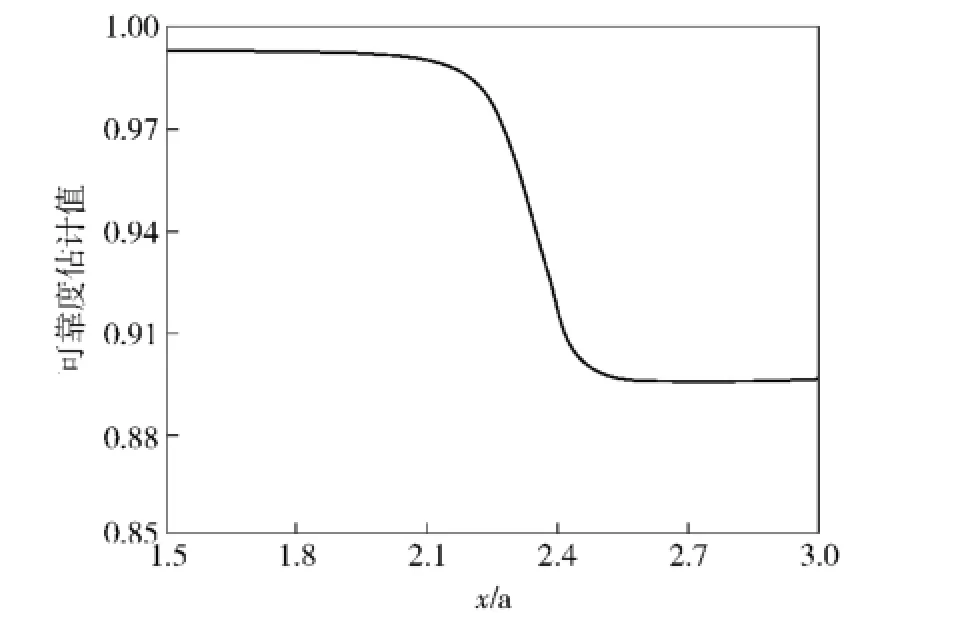
图5 可靠性估计真值函数曲线Fig.5 Estimated true value function curve of reliability

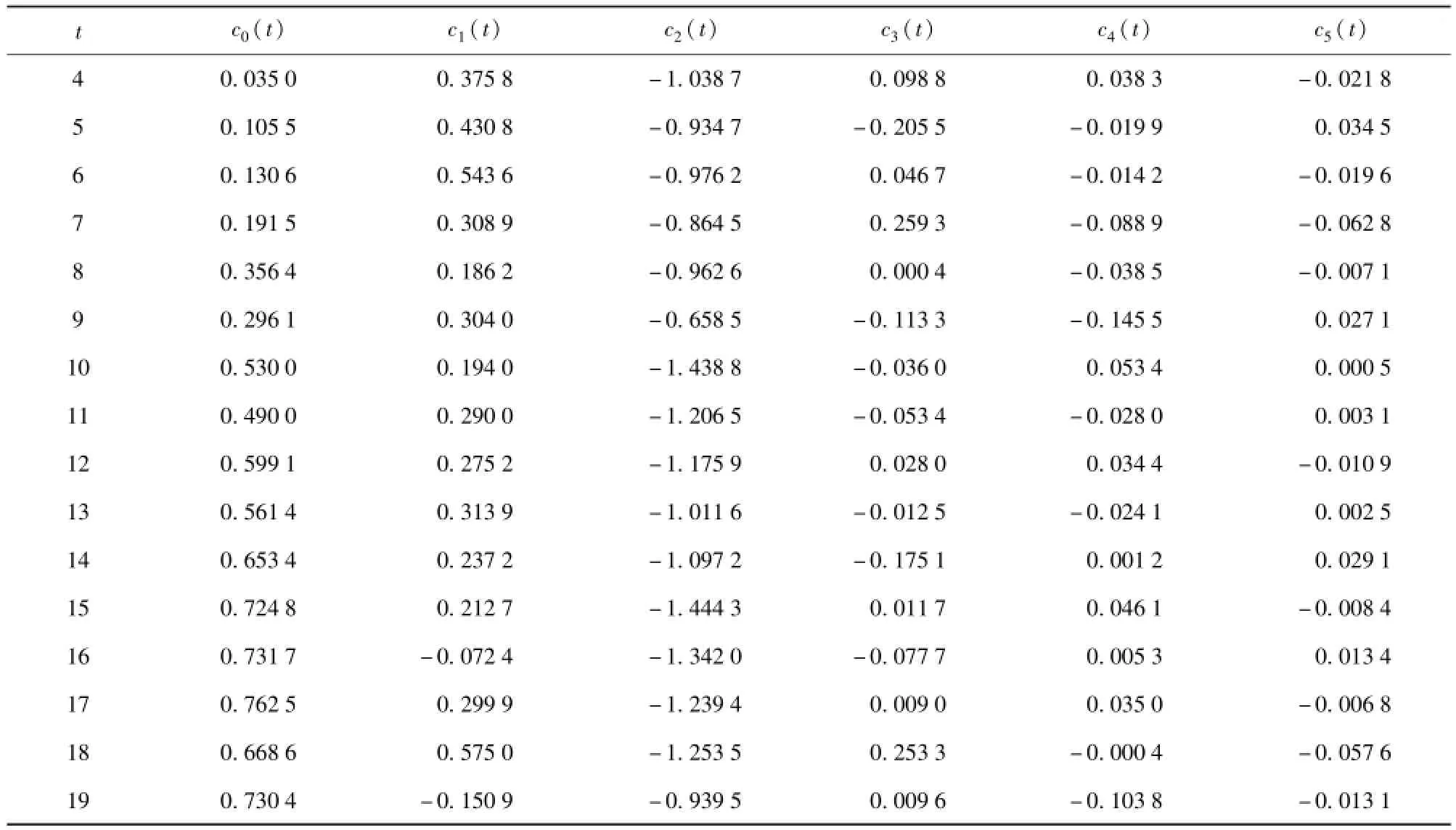
表3 改变抽样个数所得各个拉格朗日乘子Tab.3 Lagrange multipliers obtained by changing the number of samples

因此，参数c0的估计区间:［c0L，c0U］=［0.359 4，0.592 4］.

同样算得参数c1的估计区间:［c1L，c1U］=［0.1934，0.363 0］；参数c2的估计区间:［c2L，c2U］=［-1.213 1，-0.998 8］；参数c3的估计区间:［c3L，c3U］=［-0.016 3，0.010 3］；参数c4的估计区间:［c4L，c4U］=［-0.043 2，0.011 1］；参数c5的估计区间:［c5L，c5U］=［-0.019 3，0.007 6］.

改变每次抽样个数，共抽取30 000次，可得映射参数如表4所示。

经过计算，参数a、b的估计值分别为

分别将拉格朗日乘子的上限或下限值，映射参数的点估计值代入（24）式中，由排列组合原理和最大熵方法，可得64个概率密度函数。

经过计算，由最小不确定性原理可得:当c0= c0L=0.359 4，c1=c1U=0.363 1，c2=c2U=-0.998 8，c3=c3U=0.010 3，c4=c4U=0.011 1，c5=c5L= -0.019 3时，可得到可靠性函数的上限曲线RU（x）；

当c0=c0U=0.592 4，c1=c1L=0.193 4，c2=c2L= -1.2131，c3=c3L=-0.016 3，c4=c4L=-0.0432，c5=c5L=-0.019 3时，可得到可靠性函数的下限曲线RL（x）.如图6所示。

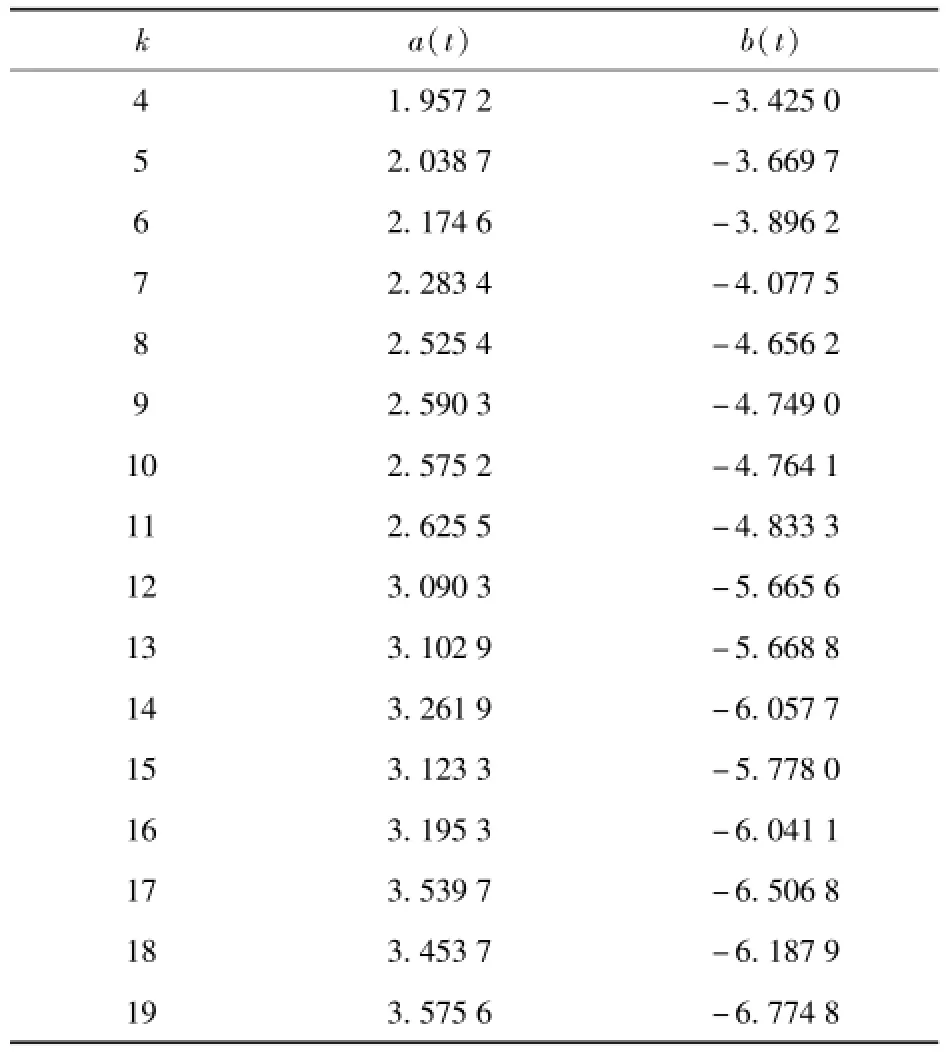
表4 改变抽样个数所得映射参数Tab.4 Mapping parameters obtained by changing the number of samples

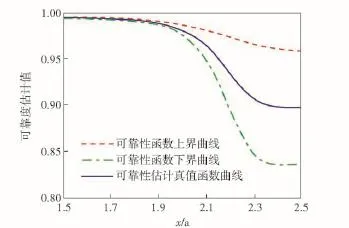
图6 可靠性函数曲线Fig.6 Curves of reliability functions

由图6可知:可靠性函数取值随着自变量时间的增大而逐渐减小，这是符合工程实际的。而且在x=1.9 a之前，可靠性函数上下限曲线图均与可靠性估计真值函数曲线图基本完全重合。在x=1.9 a之后，随着时间的增加，可靠性函数上下限曲线均越来越偏离可靠性估计真值函数曲线。这是因为在当前时间段内，对可靠性函数估计的不确定度较小。随着时间变量的增大，可靠性函数的估计难度逐渐增大，对可靠性函数估计的不确定度也逐渐增大，即上下限越来越偏离估计真值。

设可靠性系数rc=0.1，置信水平P=90%，即显著性水平为α=0.1，计算出估计真值x0:x0= 2.375 a.可靠性函数的区间估计为

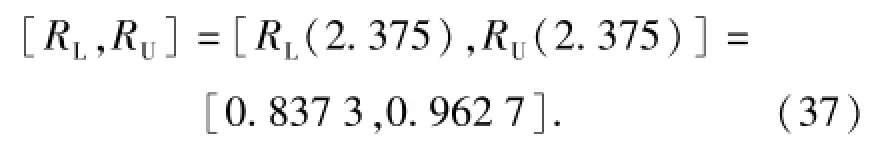
案例3 某电子产品寿命的概率分布未知，对其进行模拟实验，得到的无失效数据如下:

用自助法每次抽取10个数据，共抽取30 000次，所得数据如图7所示。

图7 自助法获取样本数据Fig.7 Sample data obtained by bootstrap method

基于最大熵法可得:映射参数a0=0.150 4，b0=-5.412 8.拉格朗日乘子（c00，c10，c20，c30，c40，c50）=（-2.473 8，-0.321 1，-0.994 8，-0.023 4，-0.031 2，0.004 7）.

由（25）式可计算出概率密度估计真值函数f0（x），将f0（x）代入（26）式、（27）式、（28）式中，可得可靠性估计真值函数R0（x），如图8所示。

改变每次抽样个数t，共抽取30 000次，可得拉格朗日乘子如表5所示。

设置信水平P=90%，即α=0.1，将所得的7个c0值作为样本进行自助再抽样可得:置信区间的下边界值c0L=-2.772 4，置信区间的上边界值c0U= -2.561 2.

因此，参数c0的估计区间:［c0L，c0U］=［-2.772 4，-2.561 2］.

同样算得参数c1的估计区间:［c1L，c1U］=［-0.224 7，-0.095 6］；参数c2的估计区间:［c2L，c2U］=［-0.985 3，-0.785 4］；参数c3的估计区间:［c3L，c3U］=［0.002 0，0.032 5］；参数c4的估计区间:［c4L，c4U］=［-0.058 1，0.022 5］；参数c5的估计区间:［c5L，c5U］=［-0.002 6，0.003 1］.

表5 改变抽样个数所得各个拉格朗日乘子Tab.5 Lagrange multipliers obtained by changing the number of samples

图8 可靠性估计真值函数曲线Fig.8 Estimated true value function curve of reliability

改变每次抽样个数，共抽取30 000次，可得映射参数如表6所示。

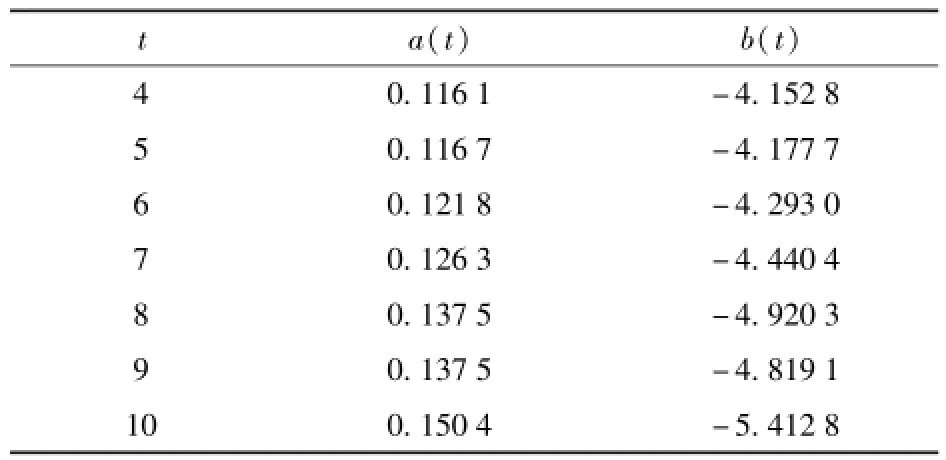
表6 改变抽样个数所得映射参数Tab.6 Mapping parameters obtained by changing the number of samples

经过计算，参数a、b的估计值分别为

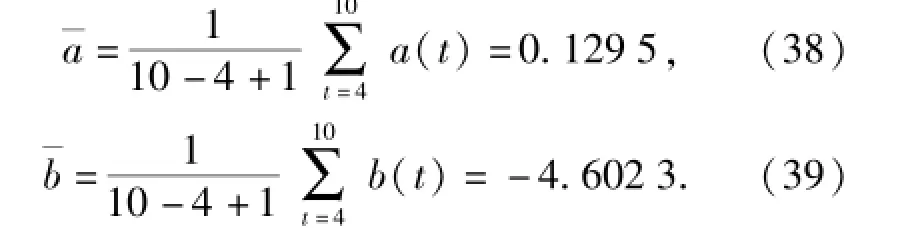
分别将拉格朗日乘子的上限或下限值，映射参数的点估计值代入（24）式中，由排列组合原理和最大熵方法，可得64个概率密度函数。

经过计算，由最小不确定性原理可得:当c0=c0L= -2.772 4，c1=c1U=-0.095 6，c2=c2U=-0.785 4，c3=c3U=0.032 5，c4=c4U=0.022 5，c5=c5L= -0.002 6时，可得到可靠性函数的上限曲线RU（x）；当c0=c0U=-2.561 2，c1=c1L=-0.224 7，c2=c2L=-0.985 3，c3=c3U=0.002 0，c4=c4L= -0.058 1，c5=c5U=0.003 1时，可得到可靠性函数的下限曲线RL（x）.如图9所示。

图9 可靠性函数曲线Fig.9 Curves of reliability functions

由图9可知:可靠性函数取值随着自变量时间的增大而逐渐减小，这是符合工程实际的。而且在x=33 h之前，可靠性函数上下限曲线均与可靠性估计真值函数曲线基本完全重合。在x=33 h之后，随着时间的增加，可靠性函数上下限曲线均越来越偏离可靠性估计真值函数曲线。这是因为在当前时间段内，对可靠性函数估计的不确定度较小。随着时间变量的增大，可靠性函数的估计难度逐渐增大，对可靠性函数估计的不确定度也逐渐增大，即上下限值越来越偏离估计真值。

取可靠性系数rc=0.1，置信水平P=90%，即显著性水平为α=0.1，计算出估计真值x0:x0= 47.5 h.

可靠性函数的区间估计:

案例4 根据文献［19］，机电设备寿命T服从对数正态分布LN（μ，σ2）时。4台电机分别工作到3 782.2 h、4 212.6 h、4 219.2 h和4 476.2 h均未失效。由于试验数据收集的困难性，希望利用上述数据对该型号电机的可靠性进行评估。

用自助法每次抽取4个数据，共抽取10 000次，所得数据如图10所示。

图10 自助法获取样本数据Fig.10 Sample data of bearings obtained by bootstrap method

基于最大熵法计算可得:映射参数a0=0.003 0，b0=-12.476 7.拉格朗日乘子（c00，c10，c20，c30，c40，c50）=（-7.272 5，1.176 6，0.038 2，-0.637 4，-0.053 8，0.071 0）.

由（25）式可计算出概率密度估计真值函数f0（x），将f0（x）代入（26）式、（27）式、（28）式中，可得可靠性估计真值函数R0（x），如图11所示。

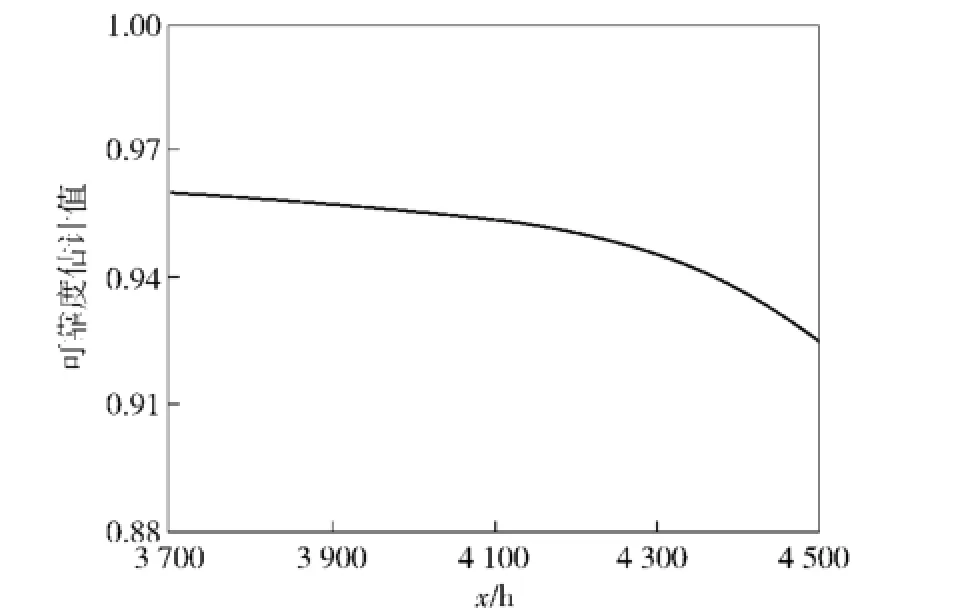
图11 可靠性估计真值函数曲线Fig.11 Estimated true value function curve of reliability

运用多层自助最大熵方法计算出的R0（4 000）= 0.955 8，R0（4 500）=0.925 0.文献［19］中运用Bayes方法计算出当λ=0.2时，μ的估计值为10.721 8，σ的估计值为1.767 3，从而可得R（4 000）=0.915 2；R（4 500）=0.904 4.可见两种方法计算结果分别相差0.040 6和0.020 6，多层自助最大熵方法的可靠性估计真值结果与用Bayes方法的可靠性估计真值结果误差很小。因此自助最大熵方法获得的可靠性估计真值函数的拟合效果跟Bayes方法的估计结果基本一致。自助最大熵方法可以自动识别样本数据内部规律，从而计算出小样本数据（n=4）的概率分布函数。在数据处理过程中，并未利用已知的概率分布先验信息。因此，用多层自助最大熵方法评估机械产品的可靠性是有效且可行的。

值得注意的是，由于样本数据较少，无法通过改变抽样个数获得拉格朗日乘子的样本数据，因此无法进行可靠性区间估计。进行可靠性区间估计需要原样本数据个数n≥7.

案例5 针对案例4，进行模拟试验，得到的无失效数据如下:

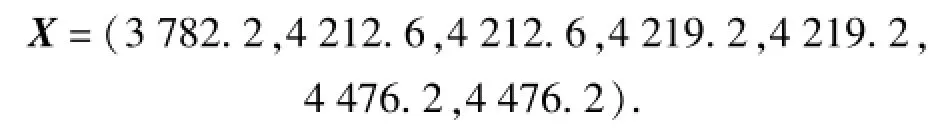
用自助法每次抽取7个数据，共抽取10 000次，所得数据如图12所示。

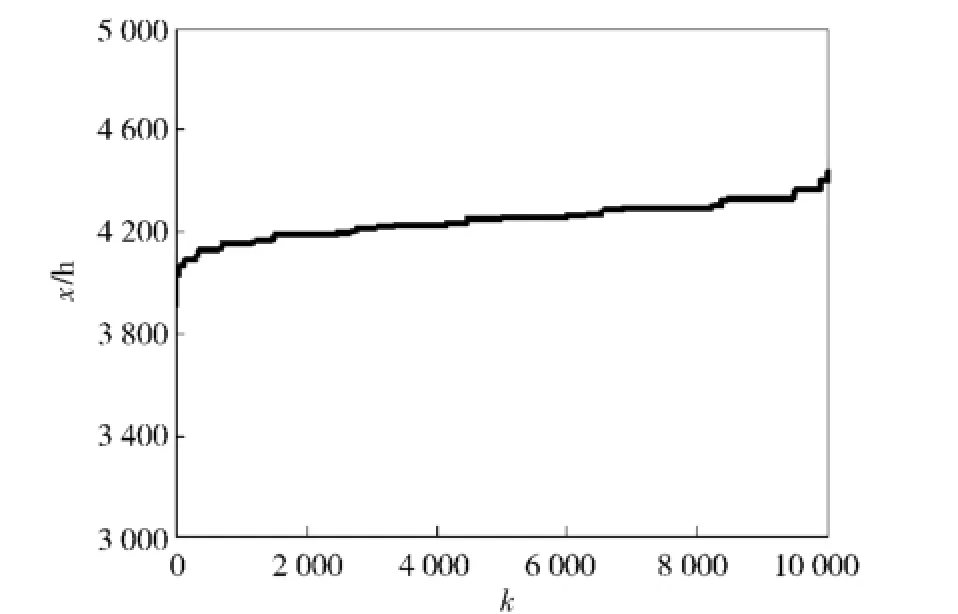
图12 自助法获取样本数据Fig.12 Sample data obtained by bootstrap method

基于最大熵法可得:映射参数a0=0.009 2，b0=-38.354 0.拉格朗日乘子（c00，c10，c20，c30，c40，c50）=（-5.653 8，1.294 6，-1.345 5，0.412 5，0.045 0，0.092 4）.

由（25）式可计算出概率密度估计真值函数f0（x），将f0（x）代入（26）式、（27）式、（28）式中，可得可靠性估计真值函数R0（x），如图13所示。

改变每次抽样个数t，共抽取30 000次，可得拉格朗日乘子如表7所示。

设置信水平P=90%，即α=0.1，将所得的7个c0值作为样本进行自助再抽样可得:置信区间的下边界值c0L=-5.804 9，置信区间的上边界值c0U= -5.703 2.

因此，参数c0的估计区间:［c0L，c0U］=［-5.804 9，-5.703 2］.

同样算得参数c1的估计区间:［c1L，c1U］=［1.248 6，1.624 0］；参数c2的估计区间:［c2L，c2U］=［-1.582 4，-0.704 4］；参数c3的估计区间:［c3L，c3U］=［0.002 0，0.032 5］；参数c4的估计区间:［c4L，c4U］=［-0.098 7，0.082 6］；参数c5的估计区间:［c5L，c5U］=［-0.065 2，0.091 5］.

改变每次抽样个数，共抽取30 000次，可得映射参数如表8所示。

图13 可靠性估计真值函数曲线Fig.13 Estimated true value function curve of reliability

表7 改变抽样个数所得各个拉格朗日乘子Tab.7 Lagrange multipliers obtained by changing the number of samples

表8 改变抽样个数所得映射参数Tab.8 Mapping parameters obtained by changing thenumber of samples

经过计算，参数a、b的估计值分别为

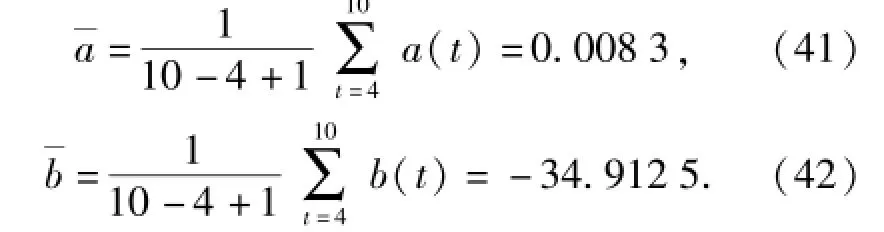
分别将拉格朗日乘子的上限或下限值，映射参数的点估计值代入（24）式中，由排列组合原理和最大熵方法，可得64个概率密度函数。

经过计算，由最小不确定性原理可得:当c0= c0L=-5.804 9，c1=c1U=1.624 0，c2=c2U=-0.704 4，c3=c3U=0.032 5，c4=c4U=0.082 6，c5=c5U=0.091 5时，可得到可靠性函数的上限曲线RU（x）；当c0= c0U=-5.703 2，c1=c1L=1.248 6，c2=c2U=-0.704 4，c3=c3L=0.002 0，c4=c4L=-0.098 7，c5=c5L= -0.065 2时，可得到可靠性函数的下限曲线RL（x）.如图14所示。

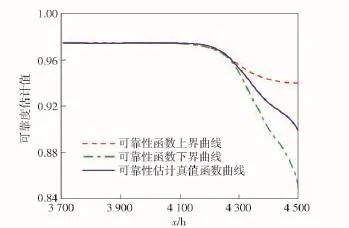
图14 可靠性函数曲线Fig.14 Curves of reliability functions

由图14可知:可靠性函数取值随着自变量时间的增大而逐渐减小，这是符合工程实际的。而且在x=4 230 h之前，可靠性函数上下限曲线均与可靠性估计真值函数曲线基本完全重合。在x=4 230 h之后，随着时间的增加，可靠性函数上下限曲线均越来越偏离可靠性估计真值函数曲线。这是因为在当前时间段内，对可靠性函数估计的不确定度较小。随着时间变量的增大，可靠性函数的估计难度逐渐增大，对可靠性函数估计的不确定度也逐渐增大，即上下限值越来越偏离估计真值。

取可靠性系数rc=0.1，置信水平P=90%，即显著性水平为α=0.1，计算出估计真值x0:x0= 4 425.4 h.可靠性函数的区间估计:

3 讨论

1）对于概率分布已知的产品寿命可靠性评估问题，自助最大熵方法的评估误差很小。案例1用多层自助最大熵法计算出的R0（577）=0.995 2与文献［17］中运用Bayes方法计算出的R（577）= 0.984 5相差0.010 7；R0（677）=0.994 5与文献［17］中运用Bayes方法计算出的R（677）=0.976 2相差0.018 3.文献［18］中运用Bayes方法计算出R（3）=0.916 4，案例2运用多层自助最大熵法计算出的R0（3）=0.898 03，二者相差0.018 37.案例4运用多层自助最大熵方法计算出的R0（4 000）= 0.955 8，R0（4 500）=0.925 0.文献［19］中运用Bayes方法计算出R（4 000）=0.915 2，R（4 500）= 0.904 4，两种方法计算结果分别相差0.040 6和0.020 6.试验案例1、案例2、案例4表明运用自助最大熵方法得到的可靠性评估结果与运用Bayes方法得到的评估结果基本相同。这是因为最大熵方法能够对未知的概率分布做出主观偏见为最小的最佳估计，可以自动识别样本数据内部规律，从而计算出样本数据个数极少（n≥4）条件下的概率分布函数。多层自助最大熵法在数据处理过程中，并未利用已知概率分布（Weibull分布、指数分布、对数正态分布）这一信息。

2）对于概率分布未知的产品寿命可靠性评估问题，古典统计理论无法解决。而案例3运用多层自助最大熵方法，计算得到R0（56.97）=0.898 9；案例5运用多层自助最大熵方法计算得到R0（4 500）= 0.897 5.试验案例表明多层自助最大熵方法不但适用于概率分布已知的产品寿命可靠性评估问题，也适用于概率分布未知的产品寿命可靠性评估问题。

3）对于可靠性函数的区间估计问题，现有方法无法解决。本文中的多层自助最大熵方法把拉格朗日乘子当作变量，对可靠性函数进行区间估计，得出结论:可靠性函数取值随着自变量时间的增大而逐渐减小，在一定范围内，可靠性函数上下限曲线图与可靠性估计真值函数曲线图基本完全重合。超出该范围，可靠性函数上下限曲线均越来越偏离可靠性估计真值函数曲线。

4）实际应用中，一般在达到产品无失效数据样本最大值的一半之前，可靠性函数上下限曲线图与可靠性估计真值函数曲线图基本完全重合。如案例1中x=700 h＞1/2×924=462 h，案例2中x= 1.9 a＞1/2×3=1.5 a，案例3中x=33 h＞1/2× 56.97=28.485 h.

4 结论

将拉格朗日乘子当做变量，提出多层自助最大熵方法，以解决机械产品的乏信息可靠性评估问题。该方法对概率分布没有要求，可以有效地解决乏信息条件下无失效数据的可靠性评估问题与可靠性函数的区间估计问题，试验证明该方法是对现有可靠性评估方法的有益补充。

（References）

［1］ 傅惠民，张勇波.Weibull分布定时无失效数据可靠性分析方法［J］.航空动力学报，2010，25（12）:2807-2810. FU Hui-min，ZHANG Yong-bo.Method of reliability analysis for time truncated zero-failure data based on Weibull distribution［J］. Journal of Aerospace Power，2010，25（12）:2807-2810.（in Chinese）

［2］ 王凭慧，范本尧，傅惠民.卫星推力器可靠性评估和寿命预测［J］.航空动力学报，2004，19（6）:745-748. WANG Ping-hui，FAN Ben-yao，FU Hui-min.Reliability assessment and life prediction for satellite engine［J］.Journal of Aerospace Power，2004，19（6）:745-748.（in Chinese）

［3］ 李宝盛，何洪庆.“小子样、零失效”情况下寿命可靠度的置信分析方法［J］.兵工学报，2001，22（2）:234-237. LI Bao-sheng，HE Hong-qing.Method of confidence analysis for life reliability on small and zero failure samples［J］.Acta Armamentarii，2001，22（2）:234-237.（in Chinese）

［4］ 蒲星.一种无失效数据可靠性分析的方法［J］.电子质量，2014（7）:29-31. PU Xing.A method for reliability analysis of zero-failure data［J］. Journal of Electronic Quality，2014（7）:29-31.（in Chinese）

［5］ 但召江，楼洪梁，李兴林，等.无失效数据下滚动轴承的可靠性估计［J］.轴承，2013（9）:22-24. DAN Shao-jiang，LOU Hong-liang，LI Xing-lin，et al.Reliability estimation for rolling bearings based on zero-failure data［J］.Journal of Bearing，2013（9）:22-24.（in Chinese）

［6］ Jiang P，Lim J H，Zuo M J，et al.Reliability estimation in a Weibull lifetime distribution with zero-failure field data［J］. Quality and Reliability Engineering International，2010，26（7）: 691-701.

［7］ Nam J S，Kim H E，Kim K U.A new accelerated zero-failure test model for rolling bearings under elevated temperature conditions［J］.Journal of Mechanical Science and Technology，2013，27（6）:1801-1807.

［8］ Bailey R T.Estimation from zero-failure data［J］.Risk Analysis，1997，17（3）:375-380.

［9］ Kwon Y.Design of Bayesian zero-failure reliability demonstration test for products with Weibull lifetime distribution［J］.Journal of Applied Reliability，2014，14（4）:220-224.

［10］ Kwon Y.The effect of scale parameter in designing reliability demonstration test for lognormal lifetime distribution［J］.Journal of Applied Reliability，2014，14（1）:53-57.

［11］ 夏新涛，陈晓阳，张永振，等.两个数据序列的灰关系及其工程应用的两个例子［J］.兵工学报，2008，29（1）:73-77. XIA Xin-tao，CHEN Xiao-yang，ZHANG Yong-zhen，et al.E-valuation for stability of manufacturing process based on grey relation［J］.Acta Armamentarii，2008，29（1）:73-77.（in Chinese）

［12］ 贾波，刘福，雷正伟.基于最大熵方法对测量数据估计的改进方法研究［J］.价值工程，2010（28）:228-230. JIA Bo，LIU Fu，LEI Zheng-wei.Study on evaluation of measurement result based on improved maximum entropy method［J］. Journal of Value Engineering，2010（28）:228-230.（in Chinese）

［13］ 夏新涛，孟艳艳，邱明.用灰自助泊松方法预测滚动轴承振动性能可靠性的变异过程［J］.机械工程学报，2015，51（9）: 97-103. XIA Xin-tao，MENG Yan-yan，QIU Ming.Forecasting for variation process of reliability of rolling bearing vibration performance using grey bootstrap Poisson method［J］.Journal of Mechanical Engineering，2015，51（9）:97-103.（in Chinese）

［14］ 胡松伟.最大熵法在发射装置可靠性评估中的应用［J］.四川兵工学报，2014，35（5）:31-33. HU Song-wei.Maximum entropy method application on missile launching system reliability evaluation［J］.Journal of Sichuan Ordnance，2014，35（5）:31-33.（in Chinese）

［15］ Yeom D H，Bae S G.A constraint-based maximum entropy sampling method for Kriging models in fuel cell applications［J］. Quality and Reliability Engineering International，2013，29（6）: 819-828.

［16］ Young H S，Byung M K.Reliability bound based on the maximum entropy principle with respect to the first truncated moment［J］.Journal of Mechanical Science and Technology，2010，24（9）:1891-1900.

［17］ 茆诗松，夏剑锋，管文琪.轴承寿命试验中无失效数据的处理［J］.应用概率统计，1993，9（3）:326-331. MOU Shi-song，XIA Jian-feng，GUAN Wen-qi.Processing of zero-failure data in bearing life test［J］.Chinese Journal of Applied Probability and Statistics，1993，9（3）:326-331.（in Chinese）

［18］ 孙亮，徐廷学，王冬梅.某型导弹无失效数据的处理方法［J］.战术导弹技术，2004（3）:29-32. SUN Liang，XU Ting-xue，WANG Dong-mei.Process method for zero-failure data of certain type missile［J］.Tactical Missile Technology，2004（3）:29-32.（in Chinese）

［19］ 孙建中.机电设备无失效数据的可靠性评估［J］.舰船科学技术，2006，28（1）:50-53. SUN Jian-zhong.Reliability estimation of zero-failure data for mechanical and electrical products［J］.Ship Science and Technology，2006，28（1）:50-53.（in Chinese）

Reliability Evaluation Based on Hierarchical Bootstrap Maximum Entropy Method

XIA Xin-tao，YE Liang，LI Yun-fei，CHANG Zhen
（School of Mechatronical Engineering，Henan University of Science and Technology，Luoyang 471003，Henan，China）

A hierarchical bootstrap maximum entropy evaluation model is proposed to analyze the life reliability of mechanical products under the condition of small samples without any prior information.Adequate sample data is obtained by using bootstrap method to re-sample the current zero-failure data samples.Based on maximum entropy method，the different Lagrange multipliers can be obtained by changing the number of samples.In order to get the interval estimation values of Lagrange multipliers，the bootstrap method is used again to re-sample the small sample data of Lagrange multipliers.The probability density functions and reliability functions are achieved by carrying on permutation and combination for the upper and lower limit values of each Lagrange multiplier，so the interval estimation values of reliability functions can be gained using minimum uncertainty principle.Experimental investigation shows that the hierarchical bootstrap maximum entropy evaluation model can effectively solve the reliability evaluation problem for zero-failure data of small samples with known or unknown probability distributions.

system assessment and feasibility analysis；reliability evaluation；hierarchical bootstrap maximum entropy method；poor information；zero-failure data；Lagrange multipliers

TB114.3

A

1000-1093（2016）07-1317-13

10.3969/j.issn.1000-1093.2016.07.022

2016-01-05

国家自然科学基金项目（51475144、51075123）

夏新涛（1957—），男，教授，博士生导师，博士。E-mail:xiaxt1957@163.com；

叶亮（1990—），男，硕士研究生。E-mail:172682823@qq.com