A novel range-Doppler imaging algorithm with OFDM radar

Xia Yang,Song Zhiyong,Lu Zaiqi,Fu Qiang

ATR Key Laboratory,National University of Defense Technology,Changsha 410073,China

A novel range-Doppler imaging algorithm with OFDM radar

Xia Yang*,Song Zhiyong,Lu Zaiqi,Fu Qiang

ATR Key Laboratory,National University of Defense Technology,Changsha 410073,China

Code symbols;Doppler effect;Estimation accuracy;Orthogonal frequency division multiplexing radar;Range-Doppler image;Single pulse

Traditional pulse Doppler radar estimates the Doppler frequency by taking advantage of Doppler modulation over different pulses and usually it requires a few pulses to estimate the Doppler frequency.In this paper,a novel range-Doppler imaging algorithm based on single pulse with orthogonal frequency division multiplexing(OFDM)radar is proposed,where the OFDM pulse is composed of phase coded symbols.The Doppler frequency is estimated using one single pulse by utilizing Doppler modulation over different symbols,which remarkably increases the data update rate.Besides,it is shown that the range and Doppler estimations are completely independent and the well-known range-Doppler coupling effect does not exist.The effects of target movement on the performances of the proposed algorithm are also discussed and the results show that the algorithm is not sensitive to velocity.Performances of the proposed algorithm as well as comparisons with other range-Doppler algorithms are demonstrated via simulation experiments.

1.Introduction

Orthogonal frequency division multiplexing(OFDM)was originally proposed as a digital modulation technique in communication fields and later on introduced into radar community by Jankiraman et al.1The first investigations on the suitability of multicarrier waveforms for radar applications were published in 2000 by Levanon.2,3As a new broadband radar signal,OFDM signal has attracted much interest due to the flexibly available spectral resources and frequency diversity characteristics.A large amount of salient work has been done on OFDM radar such as target detection and tracking,4,5direction of arrival(DOA)estimation6and synthetic aperture radar(SAR)imaging7,8fields,etc.Besides,some research work indicated that OFDM waveform was suitable for simultaneously performing both data transmission and radar sensing.9An OFDM joint radar and communication(RadCom)system had been developed in automotive radar application.10,11

Different OFDM radar signal processing methods have been developed in literature.The problem of target velocity estimation with OFDM radar was addressed in Ref.12,where MUSIC and rank reduction(RARE)algorithm were developed.A new approach based on discrete Fourier transform(DFT)for compressing the OFDM signal was proposed in Ref.13In Ref.14,the random starting phase of subcarriers was exploited to solve Doppler ambiguity.However,themethod was computationally expensive.A non-linear least squares approach was developed in Ref.15to estimate the range and velocity of a moving target using weighted OFDM(WOFDM)modulation scheme.A novel OFDM radar signal processing scheme which retrieved range and velocity information was derived in Ref.16,17However,the Doppler information was estimated over a few pulses and it had a low data update rate.

In conventional pulsed Doppler radar,Doppler is estimated by utilizing the Doppler modulation over multiple pulses.Thus,there always exist two problems:one is the conflict between unambiguous range(which is proportional to pulse repetition interval(PRI))and unambiguous Doppler(which is inverse proportional to PRI).18The other is the sensitivity of range-Doppler image to velocity.The range-Doppler image would be distorted if target velocity is high and usually velocity compensation is demanded.19Besides,in order to improve Doppler resolution,the accumulation time is always long.Accordingly,the data update rate is reduced.

In this paper,a novel range-Doppler imaging algorithm with OFDM pulse radar is proposed.The Doppler frequency is estimated within one single pulse by utilizing Doppler modulation over different symbols.First the received signal model of OFDM radar based on point target assumption is derived.Then a range-Doppler imaging algorithm which requires only one single pulse is derived.The proposed algorithm is compared with that in Ref.16and performance losses due to target movement are also discussed in detail.Finally,numerical examples are provided to demonstrate performances of the proposed algorithm.

2.Received signal model with OFDM radar

We consider a monostatic pulse radar transmitting only one single pulse which is composed ofKOFDM symbols.The advantage of this waveform scheme is the ability to avoid high value of peak to mean envelope power ratio(PMEPR).2Fig.1 shows the time and frequency structure of the OFDM pulsed waveform.

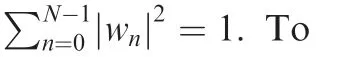
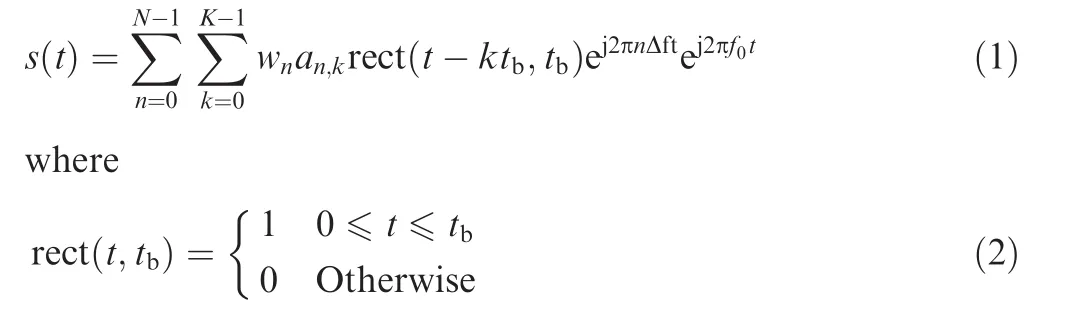
Fig.1 Time and frequency structure of OFDM waveform.

andf0accounts for the carrier frequency.an,krepresents the phase code applied on thekth symbol of thenth subcarrier.In this paper,the complex phase codes are assumed to have unit magnitude,i.e.|an,k|=1.

ConsideringLpoint targets,Ri,0andvi(i=1,2,...,L)are the initial range and radial velocity.The received signal in a noise-free scenario can be written as

where ρidenotes the complex scattering coefficient corresponding to theith target and τi=2(Ri,0+vit)/cis the roundtrip delay.cis the propagation speed.Substituting Eq.(1)into Eq.(3),after demodulation we get

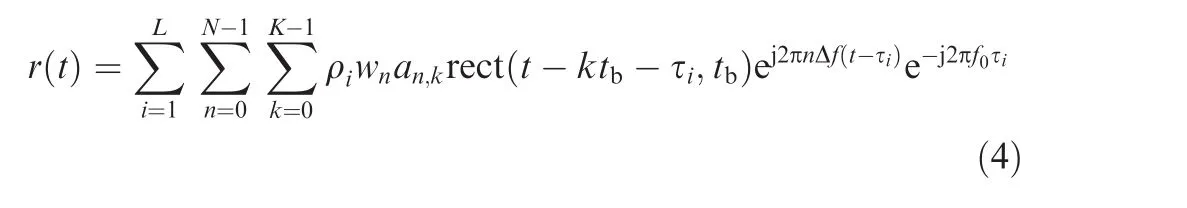
Without loss of generality,letL=1 and Eq.(4)is simplified to

The sampling rate is assumed to befs=Band sampling time ist=p/Ntb+ktb(p=0,1,...N-1).Thus,the discrete form of the complex baseband OFDM signal echo is given by

wherefd=2v/cf0denotes the Doppler frequency.

3.Range-Doppler imaging algorithm

3.1.Range-Doppler imaging algorithm based on single pulse

In an OFDM radar system one single pulse is composed of several symbols and the Doppler modulation over different symbols can be utilized to estimate the Doppler frequency.This is similar to the conventional Doppler estimation method which utilizes Doppler modulation over different pulses.A detailed description of the proposed algorithm will be given in this section.

In Eq.(6),the Doppler information is mainly concentrated on the term e-j2π（fd+nΔf2v/c）（ptb/N+ktb），which can be divided into two parts:Δ1=e-j2πf02v/c（ptb/N+ktb）represents Doppler modulation over the pulse and Δ2=e-j2πnΔf2v/c（p/Ntb+ktb）is the Doppler modulation of subcarriers over the pulse.The relationship between Δ1and Δ2is dependent on the bandwidth tolerated by the system and the carrier frequency.Taking X-band(10 GHz)radar for example,the Doppler frequency and maximum Doppler frequency of subcarrier(which can be calculated asB(2v/c))with different bandwidths and velocities are shown in Table 1.

As shown in Table 1,nΔf(2v/c)≪f0(2v/c)(n=0,1,...,N-1)ifB≪f0is satisfied.In other words,the effect of Δ2can be ignored(Δ1·Δ2≈ Δ1).Thus,Eq.(6)is rewritten as

In Eq.(7),e-j2πfd（ptb/N+ktb）can be divided into two parts:β1=e-j2πfdptb/Nrepresents Doppler effect within single symbol and β2=e-j2πfdktbrepresents Doppler effect over different symbols.Substitutingtb=1/Δfinto β1, β1is simplified to e-j2π（fd/Δf）p/N(p=0,1,...,N-1)which is dependent on Doppler frequency and subcarrier spacing.Here,we still take X-band(10 GHz)radar for example and the subcarrier frequency spacing is assumed to be 1 MHz.From Table 2 we know thatfd/Δf≈ 0 for low velocities,which results in β1≈ 1.Eq.(7)is simplified to

From Eq.(8)we know that the range and Doppler information are completely independent and the well-known range-Doppler coupling effect does not exist.In order to extract range and Doppler information,we have to get rid of{wn}and{an,k}.For clarity Eq.(8)is organized into matrix form

The various terms are given hereafter

Table 1 Doppler frequency with different bandwidths.

Table2fd and fd/Δfvarying with differentvelocities(Δf=1 MHz).

In Eq.(11),F-1denotes the inverse discrete Fourier transform(IDFT)matrix.The range-Doppler imaging algorithm based on single pulse with OFDM radar is shown as follows.

Step 1.Multiplying Eq.(9)with DFT matrix F yields

Step 2.With the prior knowledge on the transmitted weights,premultiplying B-1on both sides of Eq.(19)yields

Step 3.Let D= θXAΨ and according to Eqs.(13)–(18),the element in D can be calculated by

Step 4.Taking element-wise division in Eq.(21)with[A]n,kwhere[A]n,k=an,k,we obtain

Step 5.Applying a 2D-DFT withNr×Ndpoints on T,we can get the range–Doppler image of an OFDM radar scheme.

3.2.Comparison with the algorithm in Ref.16

In Ref.16,the authors exploited the phase of subcarriers and derived a signal processing scheme that retrieves an estimate of the range and the radial velocity with OFDM radar.However,the Doppler frequency was estimated by utilizing Doppler modulation over different pulses and it still belonged to the conventional way.Compared with the algorithm in Ref.16,our algorithm is able to estimate the Doppler frequency within one single pulse.In addition,the range and Doppler estimations are completely independent.We show range and Doppler resolutions of the two algorithms in Table 3,whereMandTrdenote the transmitted pulse number and pulse repetition interval,respectively.

In Table 3 we know that the range resolution is the same in two methods for the bandwidth is the same.Though the Doppler resolution in Ref.16is better,the proposed algorithm has a larger unambiguous Doppler scope.Besides,it is noticeable that classical unambiguous range does not exist in the proposed algorithm,for only one single pulse is transmitted.

Table 3 Rangeand Dopplerresolutionsofthe two algorithms.

4.Performance analysis of the proposed algorithm

In this section,we discuss performances of the proposed algorithm.We mainly focus on the performance loss including pulse compression loss and range estimation accuracy due to the target movement,which is equivalent to say that the OFDM pulse suffers from inter-carrier interference(ICI).20

4.1.Pulse compression loss

According to the proposed algorithm in Section 3.2,we know that the processing gain isG=N×K,which results from range and Doppler processing in Step 5.Besides,it is shown that the range and Doppler processing are completely independent and there is no gain loss in this step.The gain loss mainly results from Step 1 in the proposed algorithm.Specifically,takingNpoints DFT on the each column of Eq.(6)yields

Fig.2 e1(ε)versus n and s when ε=0.1 dB.

Fig.3 DFT gain loss versus the value of ε.

where Θ =(1-2v/c)n-s-fd/Δf.If target velocity is not too high, Θ ⋍n-s-fd/Δfand the gain loss mainly results fromfd/Δf.Let ε=fd/Δfande1(n,s,ε)=|sin(π (n-s- ε))/sin(π /N(n-s- ε))|which represents the DFT gain.Fig.2 shows thate1(n,s,ε)varies withnandswhere ε is fixed to 0.1(The value is normalized in decibels).It is shown thate1(n,s,ε)reaches the maximum value whenn=s.However,the value ofe1(n,s,ε)dropsoffatabout0.14 dBduetotheDopplereffect.

Furthermore,the relationship between DFT gain loss and ε is shown in Fig.3.DFT gain loss increases with the increase of the Doppler frequency.The DFT gain loss is less than 1 dB when ε＜ 0.26 while it reaches 3.92 dB when ε=0.5.Therefore,in practical applications the subcarrier spacing and the maximum Doppler frequency should satisfy Δf＞ 1/4|fd|maxsuch that the gain loss is less than 1 dB.

4.2.Doppler effect on range estimation accuracy

Letn=sand Eq.(23)is simplified to

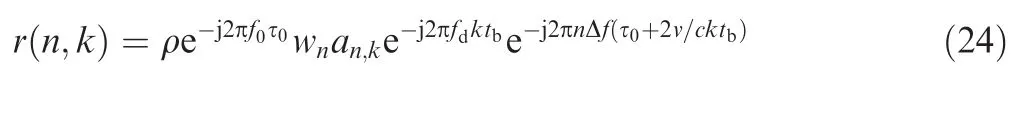
According to the algorithm described in Section 3.2,the terms{wn}and{an,k}are removed and the constant term is ignored.Thus Eq.(24)is simplified to

TakingNrpoints IDFT on each column yields

where Ω = Δfτ0+(2v/c)k-p/Nr.The error of range estimate is introduced by the term(2v/c)kwhich is proportional to the symbol number and target velocity.Moreover,|r(p,k)|=|sin(πNΩ)/sin(πΩ)|represents the range profile.Without loss of generality,letk=K-1.We show the range profile atv=100 m/s andv=3000 m/s in Fig.4(Target is located at 3030 m,K=100 andB=100 MHz).The curves show that the velocity has little impact on the range profile.

Then we show the errors of range estimate versus velocities at different symbol numbers in Fig.5.The parameters are the same as that in Fig.4.The curves show that the symbol number has little effect on the errors of range estimate whenv≤1000 m/s.Although the error of range estimate increases with increasing the number of symbol whenv＞1000 m/s,the error does notexceed one range resolution cell(Δr=1.5 m).Based on the results of Figs.4 and 5,it concludes that the error of range estimation is not sensitive to velocity and symbol number under certain conditions(Velocity is not too large.In this simulation experiment,velocity is thought to be less than 1000 m/s).

Fig.4 Range profile with v=100 m/s and v=3000 m/s.

Fig.5 Errors of range estimate versus velocities at different symbol numbers.

5.Numerical results

In this section,several numerical examples are presented to illustrate the performances of the proposed algorithm.The OFDM radar parameters are shown in Table 4.According to Table 3,the maximum Doppler frequency isfdmax=0.25-Δf=250 kHz and the corresponding maximum velocity is 3900 m/s,which is satisfied in most applications.

5.1.Performance analysis of the proposed algorithm

In this section,performances of the proposed algorithm are analyzed via several numerical examples.We mainly discuss the effects of DFT length,carrier frequency and symbol number on the performances of range-Doppler image.If not explicitly stated,simulation parameters are the same as in Table 4.

We show effects of DFT length along the Doppler dimension on the range-Doppler image in Fig.6.The value of the image is normalized in dB and we restrict it to the range[-50 0]dB to display the image clearly(the following range-Doppler images are the same).The initialrange isR0=3030 m and target flees the radar with a velocity of 150 m/s.The DFT length is 256 in Fig.6(a)and 1024 in Fig.6(b).The results show that the range-Doppler image in Fig.6(b)is more precise than that in Fig.6(a).Besides,the estimate of Doppler frequency is-11.72 kHz in Fig.6(a)and-9.766 kHz in Fig.6(b).The corresponding velocities are-175.8 m/s and-146.49 m/s,respectively.Then,we show the errors of velocity estimate versus the DFT length at different velocities in Fig.7.It concludes that the accuracy of Doppler estimate can be improved through zero padding of DFT operation along the Doppler dimension.Besides,it is noticeable that the error of velocity estimate is less than 5 m/s whenNd≥1024.

Moreover,we show the range and Doppler profile of Fig.6(b)in Fig 8.The peak values of range and Doppler sidelobe are-13.29 dB and-13.31 dB respectively.The peak values of sidelobe are high when targets exist with different backscattering strengths in a large dynamic area.Some techniques such as adding window may be used to suppress the sidelobe.However,adding window would decrease the resolution and widen the mainlobe.

In Fig.9 we have analyzed the effect of carrier frequencyf0on the range-Doppler image.Target parameters are the same as in Fig.6.We setB/f0=0.2 in Fig.9(a)andB/f0=0.01 in Fig.9(b).The two figures seem to be little different.However,the estimate of Doppler frequency is-0.9766 kHz in Fig.9(a)and-9.766 kHz in Fig.9(b).The corresponding velocities are-292.8 m/s and-146.49 m/s,respectively.Moreover,Fig.10 shows that the errors of velocity estimate vary with different carrier frequencies.As shown in Figs.9 and 10,the error of velocity estimate decreases with increasing the carrier frequency.Thus,in real applicationsB/f0shouldbe selected as small as possible to estimate the Doppler accurately.

Table 4 OFDM radar parameters.

Fig.11 shows the effect of symbol numbers on the range-Doppler image.We setK=10 in Fig.11(a)andK=100 in Fig.11(b).Target parameters are the same as in Fig.6.The estimate of Doppler frequency is the same(-9.766 kHz)in both figures.However,the Doppler resolution in Fig.11(b)is much better than that in Fig.11(a)for the Doppler resolution is dependent on Δf/K(shown in Table 4).In order to acquire good Doppler resolution,the symbol number should be large.

Fig.7 Errors of velocity estimate versus Ndat different velocities.

Fig.8 Range and Doppler profile without windowing.

5.2.Performance comparisons of the two algorithms

In this section,performances of the proposed algorithm and that in Ref.16are compared.For the range resolution(bandwidth)is the same in two algorithms,we mainly focus on accuracy of Doppler estimation.The algorithm in Ref.16is based on multiple pulses and we set the symbol number and pulse repetition interval asK=5 andTr=200 μs respectively.The pulse number isM=30.For the proposed algorithm,the parameters are the same as that in Table 5.The Doppler and velocity resolutions of the two algorithms are shown in Table 5.

In Figs.12 and 13,we show range-Doppler images of the two algorithms with target velocityv=20 m/s andv=750 m/s,respectively.The estimate of Doppler frequency is-1338 Hz in Fig.12(a)and-0.9766 kHz in Fig.12(b).The corresponding velocity is 20.07 m/s and 14.65 m/s respectively.Moreover,we show that the errors of velocity estimate vary with different velocities in Fig.14.It is shown that the accuracy of velocity estimate of the algorithm in Ref.16is better than that of the proposed algorithm,but we can increase the DFT length along Doppler dimension to improve the accuracy of Doppler estimation.

Fig.9 Range-Doppler image with different carrier frequencies when bandwidth is fixed at 100 MHz.

Fig.10 Errors of velocity estimate versus carrier frequency at different velocities.

Fig.11 Range-Doppler image with different symbol numbers.

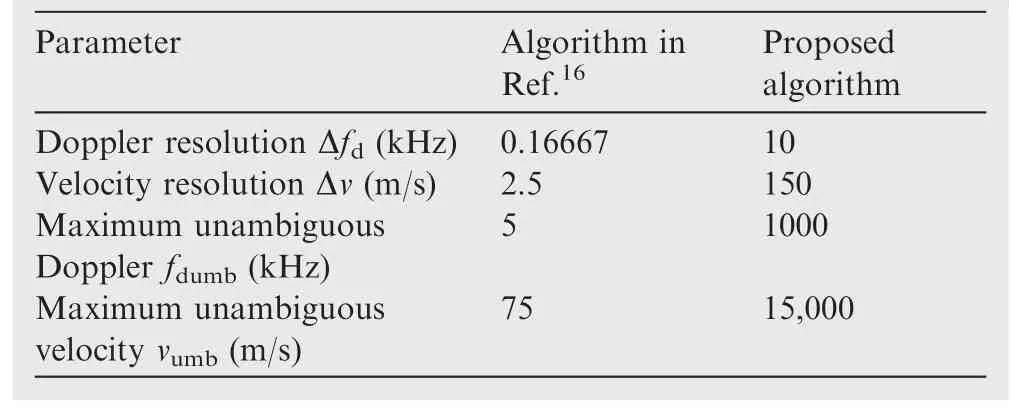
Table5 Dopplerand velocity resolution ofthe two algorithms.

In addition,the range-Doppler image(Fig.13(a))is distorted for the algorithm in Ref.16due to the high velocity.On the contrary,it has little impact on the range-Doppler image of the proposed algorithm and the estimation of velocity is 747 m/s which is close to the true value.The results show that compared with the algorithm in Ref.16,though the Doppler resolution and estimation accuracy of the proposed algorithm are not as good as that in Ref.16,it has a larger Doppler tolerance and can be applied in high speed scenarios without velocity compensation.

Finally,Fig.15 shows range-Doppler images in multitarget scenario of the two algorithms.We consider that five targets and the scattering coefficients are all equal to 1.Initial range isR0=[3020,3020,3020,3030,3010]Tm and velocities arev=[30,200,-720,25,50]Tm/s.In Fig.15(a),only four targets are visible and the Doppler frequencies of target 2 and 3 are ambiguous for the maximum unambiguous velocity is 75 m/s.However,the five targets can all be identified in Fig.15(b)and the estimate of velocity is[14.65,219.75,-732.45,29.30,43.95]Tm/s.The proposed algorithm can be used in multi-target scenario due to the large unambiguous Doppler frequency and Doppler tolerance.

Fig.12 Range-Doppler image of the two algorithms when v=20 m/s.

Fig.13 Range-Doppler image of the two algorithms when v=750 m/s.

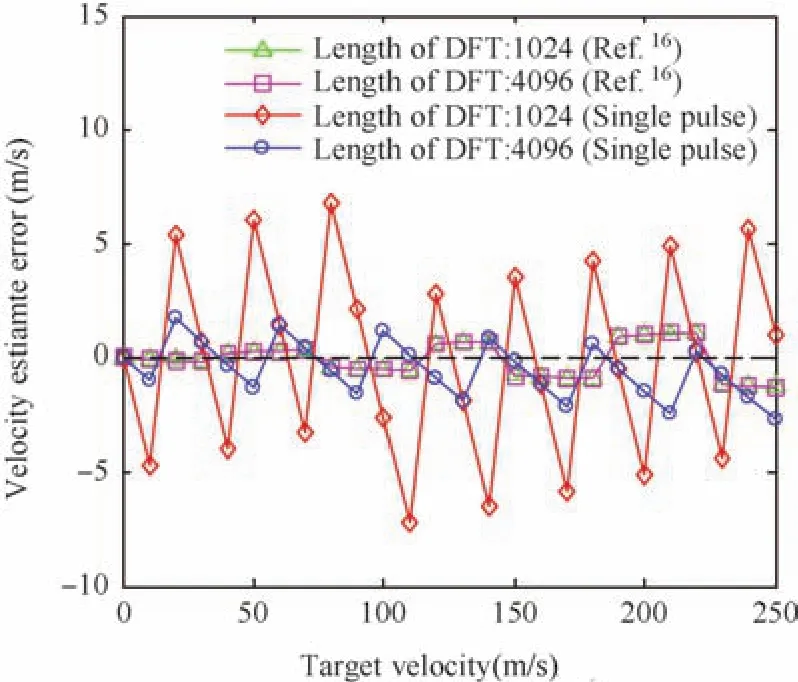
Fig.14 Errors of velocity estimate versus velocities with two algorithms.

Fig.15 Range-Doppler images of two proposed algorithm in multi-target scenarios.

6.Conclusions

In this paper,we have derived a novel range-Doppler imaging algorithm with OFDM pulsed radar.The proposed algorithm is able to estimate the Doppler frequency within a single pulse.The range and Doppler estimations are completely independent and the well-known range-Doppler coupling effect is avoided.We compared the proposed algorithm with other range-Doppler imaging algorithm(Ref.16)and showed that although the Doppler resolution of the proposed algorithm is not as well as that in Ref.16,our algorithm had a larger unambiguous Doppler frequency.Besides,we did not need conventional velocity compensation due to the high Doppler tolerance.We also analyzed the influences of target movement on the performances of the proposed algorithm and demonstrated that the target velocity had limited impact on the pulse compression gain and range profile if it was not too high.We showed that the accuracy of Doppler estimation could be improved through zero padding of DFT operations via simulation experiments.

Acknowledgement

This study was supported by the National Natural Science Foundation of China(No.61401475).

1.Jankiraman M,Wessels BJ,Genderen PV.Design of a multifrequency FMCW radar.Proceedings of the 28th European microwave conference(EuMC);1998 Oct 5–9;Amsterdam,Netherlands.Piscataway,NJ:IEEE Press;1998.p.584–9.

2.Levanon N.Multifrequency radar signals.Proceedings of IEEE 2000 international radar conference;2000 May 7–12;Alexandria,VA,USA.Piscataway,NJ:IEEE Press;2000.p.683–8.

3.Levanon N.Multifrequency complementary phase-coded radar signal.IEEE Proc Radar Sonar Navigation2000;147(6):276–84.

4.Sen S,Nehorai A.Adaptive OFDM radar for target detection in multipath scenarios.IEEE Trans Signal Process2011;59(1):78–90.

5.Sen S,Nehorai A.OFDM MIMO radar with mutual-Information waveform design for low-grazing angle tracking.IEEE Trans Signal Process2010;58(6):3152–62.

6.Wu XH,Kishk AA,Glisson AW.MIMO-OFDM radar for direction estimation.IET Radar Sonar Navig2010;4(1):28–36.

7.Garmatyuk D,Brenneman M.Adaptive multicarrier OFDM SAR signal processing.IEEE Trans Geosci Remote Sens2011;49(10):3780–90.

8.Zhang TT,Xia XG.OFDM synthetic aperture radar imaging with sufficient cyclic prefix.IEEE Trans Geosci Remote Sens2015;53(1):394–404.

9.Sturm C,Wiesbeck W.Waveform design and signal processing aspects for fusion of wireless communications and radar sensing.Proc IEEE2011;99(7):1236–59.

10.Sturm C,Braun M,Zwick T,Wiesbeck W.A multiple target Doppler estimation algorithm for OFDM based intelligent radar systems.Proceedings of the 2010 European radar conference(EuRAD);2010 Sep 30–Oct 1,Paris,France.Piscataway,NJ:IEEE Press;2010.p.73–6.

11.Braun M,Sturm C,Niethammer A,Jondral F.Parametrization of joint OFDM-based radar and communication systems for vehicular applications.Proceedings of the 20th international symposium on personal,indoor and mobile radio communications(PIMRC);2009 Sep 13–16;Tokyo,Japan.Piscataway,NJ:IEEE Press;2009.p.3020–4.

12.Vyacheslav AK,Evgeny AM.Target velocity estimation in OFDM radar based on subspace approaches.Proceedings of 14th international radar symposium(IRS);2013 June 19–21;Dresden,Germany.Piscataway,NJ:IEEE Press;2013.p.1061–6.

13.Mohseni R,Sheikhi A,Masnadi-Shirazi MA.Compression of multicarrier phase-coded radar signals based on discrete Fourier transform(DFT).Progr Electromagn Res C2008;5:93–117.

14.Tigrek R,De HJ,Genderen PV.OFDM signals as the radar waveform to solve Doppler ambiguity.IEEE Trans Aerospace Electron Syst2012;48(1):130–43.

15.Turlapaty A,Jin YW,Xu Y.Range and velocity estimation of radar targets by weighted OFDM modulation.OFDM radar.Proceedings of 2014 IEEE radar conference;2014 May 19–23;Cincinnati,OH,USA.Piscataway,NJ:IEEE Press;2014.p.1358–62.

16.Lellouch G,Mishra A,Inggs M.Impact of the Doppler modulation on the range and Doppler processing in OFDM radar.Proceedings of 2014 IEEE radar conference;2014 May 19–23;Cincinnati,OH,USA.Piscataway,NJ:IEEE Press;2014.p.803–8.

17.Lellouch,G,Mishra A,Inggs M.Processing alternatives in OFDM radar.Proceedings of 2014 international radar conference;2014 Oct 13–17;Lille,France.Piscataway,NJ:IEEE Press;2014.p.1–6.

18.Bassem RM,Atef ZE.Radar systems analysis and design using MATLAB.New York:Chapman&Hall/CRC;2004.p.72–80.

19.Levanon N,Eli M.Radar principles.Hoboken,NJ:Wiley;1998.p.168–75.

20.Armstrong J.Analysis of new and existing methods of reducing inter-carrier interference due to carrier frequency offset in OFDM.IEEE Trans Commun1999;47(3):365–9.

16 June 2015;revised 18 December 2015;accepted 20 January 2016

Available online 23 February 2016

ⓒ2016 Chinese Society of Aeronautics and Astronautics.Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.Tel.:+86 731 84576401-0.

E-mail address:xiayang2020@126.com(Y.Xia).

Peer review under responsibility of Editorial Committee of CJA.

Xia Yangreceived the M.S.degree from the National University of Defense Technology(NUDT)in 2009.He is currently a Ph.D.candidate at the ATR Key Laboratory,NUDT.His research interests include radar signal and data processing,target detection and tracking,radar imaging.

Song Zhiyongreceived the Ph.D.degree in information and communication engineering from the National University of Defense Technology(NUDT)in 2012.He is currently a lecturer at the ATR Key Laboratory,NUDT.His research interests include radar signal processing,target detection and anti-jamming.

Lu Zaiqireceived the Ph.D.degree in information and communication engineering from the National University of Defense Technology(NUDT)in 2002.He is currently an associate professor at the ATR Key Laboratory,NUDT.His research interests include radar signal processing,target tracking and information fusion.

Fu Qiangreceived the Ph.D.degree in information and communication engineering from the National University of Defense Technology(NUDT)in 2004.He is currently a professor and doctoral supervisor at the ATR Key Laboratory,NUDT.His research interests include radar system design,precise guidance and automatic target recognition.