基于改进Harris角点算法的摄像机标定技术研究

曹　兵，李文博，张云波

（南京理工大学机械工程学院，南京　210094）

基于改进Harris角点算法的摄像机标定技术研究

曹兵，李文博，张云波

（南京理工大学机械工程学院，南京210094）

针对传统的Harris角点提取算法对噪声敏感，执行效率低等不足，提出了一种改进的Harris角点提取方法；以Harris角点提取算法为基础，通过优化角点响应函数，消除系数K，提高角点提取算法的执行效率；采用改进的Harris算法对黑白棋盘表格进行内角点提取，利用张正友摄像机标定法计算USB摄像机的内外参数；实验结果证明了该方法可以有效的对黑白棋盘格内角点进行提取，准确高效，提高了摄像机的标定精度和准确性，是一种可行的摄像机标定方法。

角点提取算法；棋盘格；摄像机标定

0　引言

作为计算机视觉的“眼睛”，摄像机是获取三维视觉信息的基础，在计算机视觉中占有非常重要的地位。摄像机的参数分为外部参数和内部参数，标定的目的就是为了得到摄像机的内外参数，摄像机标定的精度直接影响整个计算机视觉系统的精度。近年来，摄像机两步标定法应用较多，其特点是将摄像机畸变与摄像机内外参数分离，逐步取得最优解［1］。典型的两步法有张正友摄像机平面标定法和Tsai摄像机平面标定法。张正友摄像机平面标定法介于传统标定法和自标定法之间，其操作简单方便，鲁棒性好且准确度较高，已经广泛应用于视觉系统。

角点提取算法主要用于获取图像特征，广泛应用于运动检测、图像匹配和目标识别等领域中，同时也是摄像机标定技术中至关重要的一部分。目前，角点提取算法主要分为两类：一类是基于轮廓曲线，如Kitchen Rosenfeld［2］、Freeman链码法［3］、Wang-Brady［4］等；另一类是基于灰度图像，如Moravec算法、Harris算法［5］、SUSAN算法［6］等，这类方法通过计算图像的梯度及边缘曲率来提取角点。

相对于其他几类角点提取算法，Harris角点提取算法的提取效果是最好的［7］。但是它对噪声较为敏感，需要人为给定系数K才能获得比较理想的效果，影响了算法的执行效率，文中将通过优化角点响应函数，提高角点提取的执行效率。本文将结合改进的Harris角点提取算法和张正友摄像机标定法对摄像机的内外参数进行标定，进一步提高了黑白棋盘格内角点提取的准确性和摄像机内外参数的标定精度.

1　Harris角点提取

Harris角点提取算子是对Moravec角点提取算子的一种改进，是一种基于信号点特征的提取算子。

1.1Moravec角点提取原理

Moravec角点提取算子的思想比较简单，如图 （1）所示，在待提取的图像上以被检测像素点为中心设置一个W*W的滑动窗口，逐个像素的移动这个窗口并检查窗口中的像素变化情况。窗口中的像素变化可以简单的分为3类：若所测像素点的邻域是平坦的，则窗口移动的过程中像素的变化不大，如图（1）中（A）所示；若所测像素点的邻域包含“边缘”，则沿边缘方向移动窗口时，像素变化很小，沿边缘的垂直方向移动窗口时，像素变化很大，如图（1）中（B）所示；若所测像素点的邻域包含“角点”，则沿任意方向移动窗口时，像素均有明显变化，如图（1）中 （C）所示。所以检测像素的变化情况，设定阀值，当像素的变化超过了设定的阈值，则被检测点即为是角点。

图1　像素变化情况图

Moravec角点提取算子用数学语言表示就是：

其中，Ex，y表示像素的变化值，wu，v为移动窗口函数，Iu，v为像素点（u，v）的灰度值，Ix+u，y+u为窗口移动后的灰度值，（x，y）表示八个移动方向。

可以看出Moravec算法只能检测窗口函数在8个基本方向上移动的变化，不能准确提取出在其它方向上产生变化的角点。由于该算法计算的是灰度强度的变化，显然，对于图像亮度变化较敏感，并且该算法对孤立点、噪声和边缘也比较敏感。

1.2Harris角点提取原理

Harris角点提取算子实质上就是对 Moravec算子的改进和优化。Moravec算子对方向的依赖性太强，只能覆盖8个基本方向的检测，Harris通过引进微分的思想使得算子可以覆盖所有方向上的检测，则式（1）就转化为：

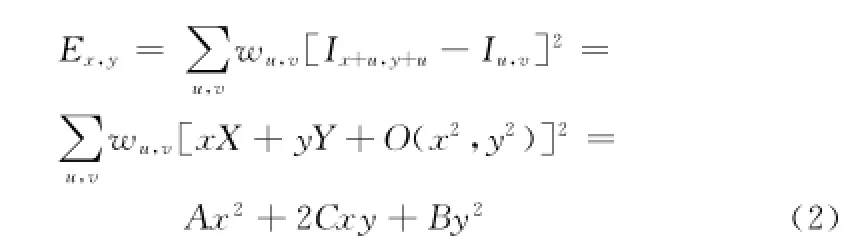
其中，X和Y是一阶灰度导数，定义如下：

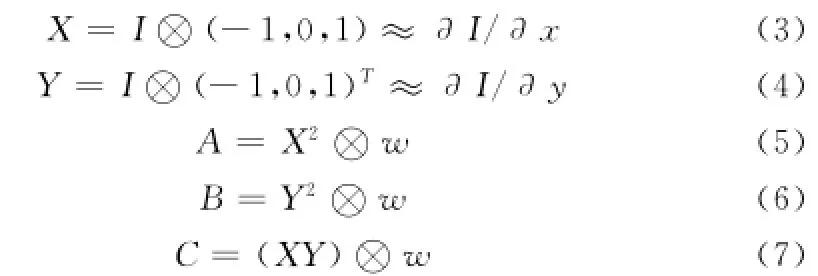
由于Moravec算子采用的是二值化的矩形窗口函数，像素的变化易受噪声干扰，Harris就采用较为平滑的高斯函数作为窗口函数：

wu，v=exp-（u2+v2）/2σ2（8）

Moravec算子对边缘的响应过于敏感，容易将边缘误判成角点，对变化量Ex，y变形为：

Ex，y=（x，y）M（x，y）T（9）

上式中，Ex，y是图像的局部自相关函数，M 是2×2的对称矩阵，M矩阵的特征值与自相关函数Ex，y的曲率成比例关系，所以通过判断M矩阵的两个特征值的大小就可以确定角点，设M矩阵的两个特征值为λ1和λ2，则存在如下3种情况：当两个曲率都很小时，λ1和λ2的值也很小，即局部自相关函数在各方向的变化量都很小，此时，目标区域为平坦区；当一个曲率较大而另一个曲率较小时，即λ1≥λ2，局部自相关函数一个方向的变化量较大，另一个方向的变化量较小，此时目标区域为“边缘”；当两个曲率都很大时，对应于特征值λ1和λ2很大，那么局部自相关函数沿各个方向的变化均较大，此时的目标区域就是“角点”。

为了避免分解自相关矩阵的特征值，Harris定义了角点响应函数（CRF）：

CRF=det（M）-k［trace（M）］2（10）

其中：det（M）=λ1λ2，trace（M）=λ1+λ2，k为经验值，建议取0.04～0.06。提取角点时，首先要设定阈值，当角点响应函数的值大于阈值时，就可以确定目标点为角点。

2　改进的Harris角点提取算法

Harris角点提取算法简单易操作，具有旋转不变性、对于图像灰度的仿射变化具有部分的不变性等优点［8］。但是Harris角点提取的质量很大程度上取决于阈值的设定，阈值设定过大会丢失一部分角点，阈值设定过小就会降低角点的提取效果。另外，角点响应函数中的系数k具有不确定性，不同的k角点的提取效果不同，如果选择了合适的k值，这种算法可以获得不错的提取效果，但合适的k需要多次调试才能获得，降低了算法的执行效率。

2.1改进算法

针对Harris角点提取算法的不足，文中通过优化角点响应函数来改进。角点响应函数是关于自相关矩阵M的2个特征值的函数，Harris提出的角点响应函数既包含det（M），又包含trace（M），而且引进了参数K，虽然可以很好的提取角点，但增加了算法的不稳定性。不妨将角点响应函数CRF简化为：

CRF=trace（M）=λ1λ2（11）

trace（M）中同时包含可λ1和λ2，通过上面的分析得知目标点是否为角点可以由λ1和λ2的取值大小来判断，所以可以通过检测trace（M）值的大小来判断目标点是否为角点，当λ1和λ2都很小时，trace（M）的值也很小；当λ1和λ2的值一大一小时，trace（M）的值较小；当λ1和λ2的值较大时，trace（M）的值就较大。可以通过设定一个较大的阈值，当trace（M）大于设定的阈值时，就可以确定目标点为“角点”。

通过上述的方法可以很好的将图像中的角点提取出来，但所提取的角点并非都是摄像机标定所需的黑白棋盘格的内角点，此时，需要对角点进行分类，将非内角点排除，排除的方法是比较目标点24邻域中的4个对角点的像素值，若4个点的像素2个较大，2个较小，则目标点就是需要的内角点，若是其他的情况，则可以排除目标点。

2.2算法实现过程

由Harris角点提取的基本原理可以得出该算法提取角点的过程可以归纳为以下5步［9］：

1）分别计算待检测图像在水平和垂直方向上的梯度Ix和Iy，则M表示为：

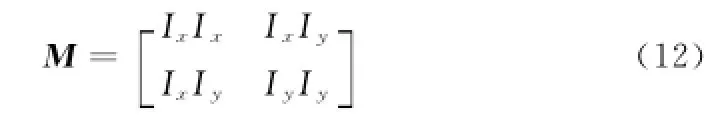
2）对计算后的图像进行高斯滤波，得到滤波后的M；

3）计算原图像上每个像素点对应的角点响应函数CRF的值；

4）对求出的CRF进行排序滤波，减小伪角点的影响，便于后面阈值的设定；

5）设定合适的阈值，提取角点，对提取的角点进行分类，选取出摄像机标定所需的黑白棋盘格的内角点。

本文通过优化Harris角点提取算子的角点响应函数，不仅保留了原算法的优点，还通过消去参数K，加强了算法的稳定性，提高了角点提取的效率。在对摄像机标定试验中用到的黑白方格靶标进行角点提取时，具有较好的应用效果。

3　张正友摄像机标定

张正友标定法［10］处于传统的摄像机标定法和摄像机自标定法之间，融合了两种方法各自的优点，所以具有较高的精确度，鲁棒性好的优点，同时又操作简便。本文利用此方法来标定单目摄像机，标定物选择了黑白棋盘格。该方法的标定步骤如下所示：

1）打印一张黑白棋盘方格图作为标靶，将其平整的贴在平面上；

2）改变摄像机和标靶的相对位置，从不同的角度拍摄多张标靶的图像；

3）提取出每张图像中的特征点，选取棋盘格的内角点作为标定点；

4）求出每张图像的平面投影矩阵H；

5）利用矩阵H求解出摄像机的内参数；

6）通过反投影变换对标定结果进行优化，得到更加准确的标定结果，同时计算出摄像机的畸变系数。

标定过程的流程图如图2所示。

图2　摄像机标定程序流程图

4　实验仿真结果分析

整个实验使用MATLAB进行编程完成，实验中采用的是USB工业摄像头。采用的平面靶标是10X12的黑白棋盘格，每个格子的长宽为20X20 mm。标定之前首先使用相机从不同的角度采集20幅图像，如图3所示。

4.1提取棋盘格角点

文中分别使用Harris角点提取算法和改进的Harris算法对五副图像进行角点提取，如表1所示，其中第一幅图像的提取结果如图4和图5所示。

从图4中可以看出，原Harris角点提取算法在第一幅图像中提取了147个角点，其中包括图像的4个角点、棋盘格的外角点和内角点等，而只有内角点才是摄像机标定所需要的。

图3　摄像机采集的图像

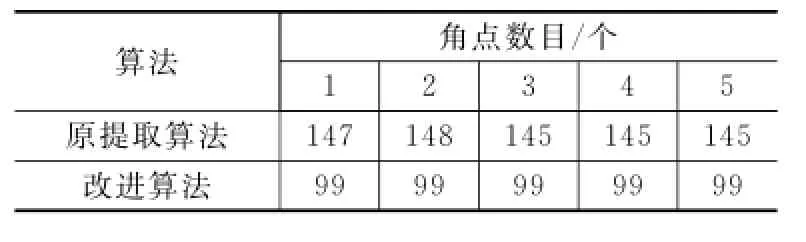
表1　角点提取情况对比表

图4 Harris角点算法提取的角点　

图5　改进的Harris算法提取的角点

从图5中看出，改进后的Harris角点提取算法同样具有较好的提取效果，而且不用再考虑参数K的取值情况，提高了算法的执行效率，同时改进算法完全只提取所需的内角点，而忽略其他类型的角点，满足摄像机标定的需要。由表1的数据可以看出改进的Harris角点算法能够准确的提取标定所需的每幅图的内角点。

4.2摄像机标定结果

使用MATLAB编写张正友摄像机标定程序实现上述的标定过程，使用图（1）所示的20副图像对USB摄像机进行标定，得到的摄像机内部参数如表（2）所示。

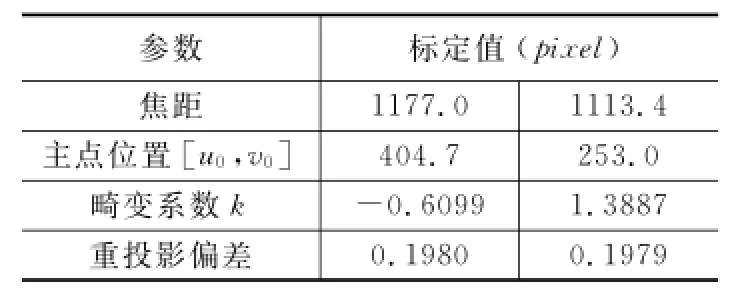
表2　摄像机内部参数

在采集图像的过程中，摄像机与棋盘格的位置一直在变化中，每幅图像的外参数矩阵不同，在此列出第一幅图像的外参数矩阵：

完成摄像机内外参数的标定后，为了检验标定结果的精度，利用标定结果对棋盘格中的内角点的世界坐标进行计算，得到对应的图像中的角点坐标，将其与提取得到的内角点坐标进行求差，可以得到棋盘格中内角点的重投影偏差，如图所示，从图中可以看出，无论是水平方向，还是垂直方向，重投影偏差总体位于［-0.5-0.5］内，平均偏差是x=0.198 0，y=0.197 9，均较小。

图6　重投影偏差分布图

5　结论

本文提出了基于改进Harris角点提取算法和张正友标定技术的摄像机标定方法。该方法有效地利用了Harris角点提取算法的优势.并对其不足之处进行改进，提高了Harris角点提取算法的执行效率，最后使用张正友标定法完成摄像机的标定，实验结果表明：本文提出的标定算法能够取得较高的标定精度，一定程度上满足了工业的需求。

［1］邱茂林，马颂德，李毅.计算机视觉中摄像机标定综述［J］.自动化学报，2000，26（1）：43-55.

［2］Kitchen I.Rosenfei.D A.Gray—level corner detection［J］.Pattern Recognition Letters，1982.1（2）：95-102.

［3］Li J，Guo S，Ye F，Shape Recognition BasedOn Freeman Chain Code［J］.Trans Tech Publications Ltd.2011.317319：2490-6.

［4］Wang H，Brady M.Real—time corner detection algorithm formotion estimation［J］.Image and Vision Computing，1995，13（9）：695-703.

［5］Harris C，Stephens M.A combined corner and edge detector［A］. Proceedings of the Fourth Alvey Vision Conference［C］.Manchester，UK，1998：147-151.

［6］Stephen M，Smith，J.Michael Brady.Susan—A New Approach to Low Level Image Processing［J］.International Journal of Computer Vision，1997，23（1）：45-78.

［7］Kitchen L，Rosenfeld A.Gray Level Corner Detection［J］.Pattern Recognition Letters，1982，3（1）：95-102.

［8］蔡胜利，张会清.基于Harris角点检测的图像旋转测量.［J］.计算机测量与控制，2011，19（1）：30-32.

［9］卢英，王慧琴，佟威.基于Harris-张正友平面标定法的摄像机标定算法［J］.西安建筑科技大学学报，2014，46（6）：860-864.

［10］Zhang Z Y.Flexible camera calibration by viewing a plane from unknown orientations［A］.Proceedings of the IEEE International Conference on Computer Vision［C］.Greece，1999：666-673.

Research of Camera Calibration Technique Based on Improved Harris Corner

Cao Bing，Li Wenbo，Zhang Yunbo
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing210094，China）

For traditional Harris corner detection algorithm is sensitive to noise，and low execution efficiency，put forward an improved Harris corner detection method.On the basis of Harris corner detection algorithm，by optimizing the corner response function，remove the coefficient K，improve the execution efficiency of corner detection algorithm.Extract the corner of black and white chessboard by using the improved Harris algorithm and calculate the internal and external parameters of USB camera by using the Zhang zheng-you camera calibration method.The results show that this method can effective to extract the corner of black and white checkerboard，accurate and efficient，improves the precision of the camera calibration and is a feasible camera calibration method.

corner extraction method；checkerboard pattern；camera calibration

1671-4598（2016）05-0213-03

10.16526/j.cnki.11-4762/tp.2016.05.060

TP391

A

2015-11-11；

2015-12-07。

曹兵（1967-），男，河南南阳人，副教授，硕士研究生导师，主要从事弹药工程与爆炸技术方向的研究。