高超音速飞行器鲁棒控制器设计

张　雪，岳丽敏，梁晓庚

（1.中国空空导弹研究院，河南　洛阳　471009；2.郑州铁路职业技术学院机电工程系，郑州　450052）

高超音速飞行器鲁棒控制器设计

张雪1，岳丽敏2，梁晓庚1

（1.中国空空导弹研究院，河南洛阳471009；2.郑州铁路职业技术学院机电工程系，郑州450052）

军事变革和信息化战场环境的变化，促使空天攻防作战成为未来作战的战场之一；临近空间高超音速飞机和导弹会对传统攻防体系带来颠覆性冲击；复杂环境对高超音速飞行器控制技术的发展提出了严峻的挑战，文章针对吸气式高超音速飞行器在飞行包线内动态特性易变、稳定性较差、不确定因素较多以及对外界扰动敏感以及整个执行机构控制能力弱和动态特性低等的控制问题，首次提出了一种能同时抑制扰动和模型不确定性的基于优化控制的鲁棒控制方法，保证飞行器能得到很好地控制，快速响应环境变化并很快回到稳定飞行的状态；采用线性矩阵不等式方法来设计飞行控制系统，给出了不确定系统稳定的条件，将反馈稳定问题转化为了一个最优控制问题；同时将闭环极点在一定区域内参与优化，进一步提高优化效率；与文献方法仿真对比结果证实了文章方法的优越性。

高超音速飞行器；鲁棒控制；线性矩阵不等式；极点配置

0　引言

随着高性能隐身飞机、无人机、临近空间高速飞行器以及空天飞机等新型威胁目标不断涌现，“空天一体、攻防兼备”成为信息化作战新的战略要求。临近空间高超音速飞机和导弹会对传统攻防体系带来颠覆性冲击，导弹及其发射平台的生存能力和突防能力受到严重挑战。

由于吸气式高超音速飞行器在飞行时气动弹性和气热弹性效应会导致机体产生一定形变，因此给系统注入了动态不确定性。此外，飞行器速度和空域变化范围很大。不同速度飞行的飞行器自身气动特性变化也很大，如升阻比、稳定性和操纵性。另外，由于飞行器的上半身较长且产生的推力较大，要求控制器更加灵敏。作为控制对象的高超声速飞行器表现有非线性、多变量、不稳定和模型不确定性等特点。此外，由于飞行器本身采用尾部升降舵面控制飞行弹道倾角，必然在控制舵面到飞行弹道角通道中引起非最小相位行为，严格限制了飞行器的轨迹控制性能。因此确保飞行器姿态相应的稳定性，适应在飞行过程中的外界飞行环境，是亟待解决的关键问题之一，也对飞行控制系统设计提出了新的研究挑战。

本文针对吸气式高超音速飞行器在飞行包线内动态特性易变、稳定性较差、不确定因素较多以及对外界扰动敏感以及整个执行机构控制能力弱和动态特性低的控制问题等，提出了一种能同时抑制扰动和模型不确定性的基于优化控制的鲁棒控制方法，以确保飞行器在复杂飞行条件下，能快速地响应环境的变化，回到稳定飞行状态，实现其航迹的有效控制。

1　飞行器建模

巡航状态下，吸气式高超音速飞行器的速度以及发动机推力应该为常值，一旦攻角受到外界影响而产生变化，会影响发动机的性能，进而导致速度和高度偏离期望值。

考虑吸气式高超音速飞行器俯仰通道的动力学μ（ft3/s2），和Iyy（slug·ft2）分别表示飞行速度，航迹角，飞行高度，飞行攻角，俯仰角速度，飞行器质量，地心引力常数以及惯性矩矩。

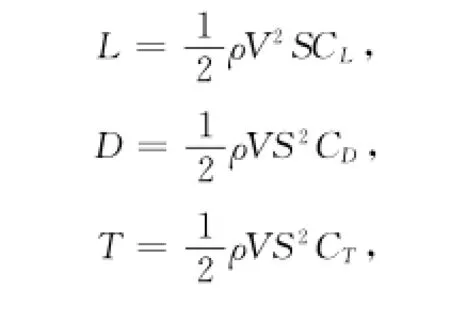
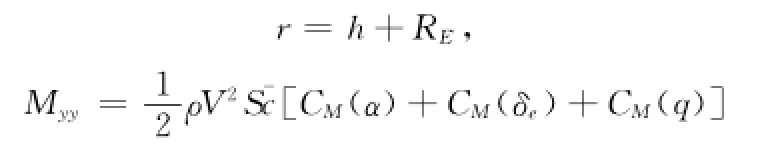
其中：S为飞行器特征面积，CL、CT分别为升力系数和推力系数。

巡航状态下，¯c表示平均气动弦长；而CM（α），CM（δe），CM（q）分别是和攻角、升降舵偏和俯仰速率相关的力矩系数。

各系数公式为：

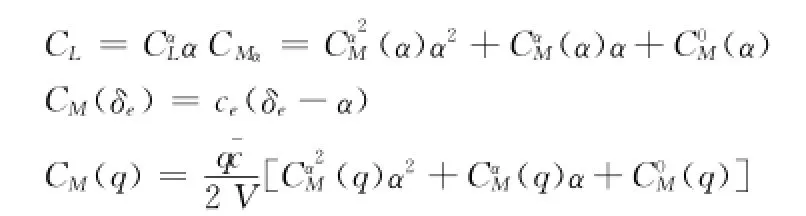
高超音速飞行器纵向运动方程可以用一个通用的多输入多输出非线性系统模型描述

其中：X表示状态向量，Uk（k=1，2）表示控制的输入向量（包括升降舵偏角δe和发动机节流阀的开度η）。

2　控制器设计

飞行器的性能指标有很多，包括稳定性、响应速度、干扰抑制、指令跟踪、鲁棒性能等等。一般的控制方法只能对单个指标进行设计，然后看设计得到的控制器能否满足其他指标，整个设计过程需要多次重复设计。

本文将最优控制器与鲁棒H∞控制方法结合，将多个性能指标转化为一个综合性能指标后设计控制器，同时在一定区域内考虑将闭环极点优化配置，可以有效提高优化效率。

基于高超音速飞行器的复杂性，为方便控制器的设计，选取巡航段的某个平衡点，研究高超音速飞行器纵向运动方程。线性化模型可以表示为：

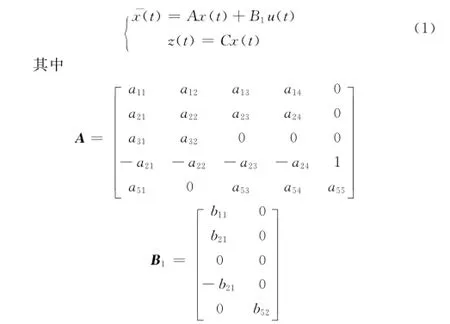
在整个巡航过程中，飞行器可能会受到外界的各种扰动和不确定的影响，为了保证系统的鲁棒性和稳定性。在被控对象的模型中引入扰动和不确定影响，则闭环系统可以表示为

其中：A∈ Rn×n为系统矩阵，B1∈ Rn×m为控制矩阵，C∈Rp×n为输出矩阵，B2为常数矩阵，ΔA表示范数有界不确定量，满足ΔA=LN（t）E

其中，矩阵L和E为具备适当维数的已知矩阵，反映了不确定参数的结构信息。N（t）为未知变量，反映了系统模型中的不确定性，且

N（t）TN（t）≤1

采用如下状态反馈控制器

u（t）=K x（t）

其中，K∈Rm×n为状态反馈增益矩阵。结构图如图1所示。

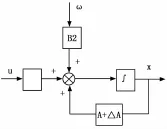
图1　结构图表示

则设计的控制器需要满足以下目标：

1）使含扰动和不确定性的闭环系统渐进稳定；

2）在零初值条件下，对于给定的正常数λ，被控输出满足H∞范数界

T（s）∞＜γ 3）极点配置：要求闭环极点位于指定区域内4）最小化基于H∞控制的性能代价函数

为了解决满足多个设计目标的控制问题，通过求解矩阵不等式来解决。由于飞控系统的稳定性和性能是最需要关心的问题。首先给出范数有界不确定性系统的渐进稳定性存在条件：

公式（1）考虑给定的系统（2）其渐进稳定且满足指定范数界的条件是存在正定对称矩阵，使得下述线性矩阵不等式成立：

（*表示共轭转置）

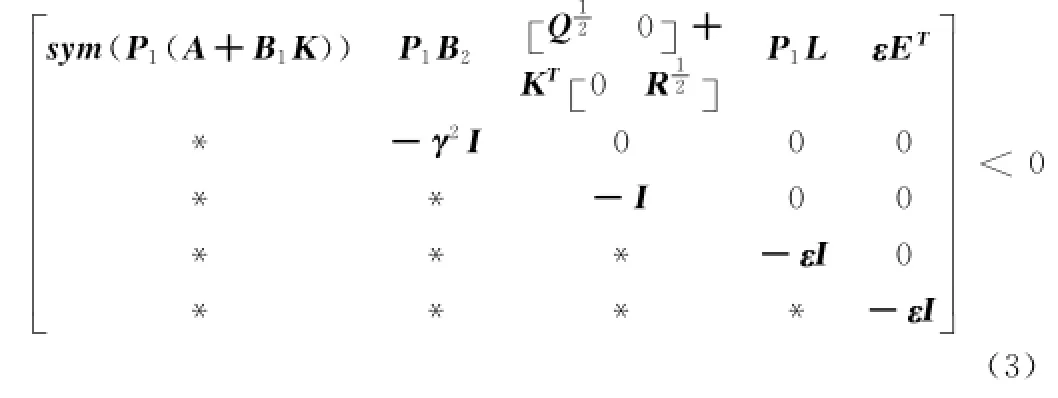
这里Q及R为相应的权函数，是用来衡量控制分量相对重要成都的加权阵，为常值矩阵。Q为对称的半正定矩阵，R为对称正定矩阵。

由于飞行器纵向模型是可控可观的，为了获得理想的闭环动态性能，考虑将极点配置到指定的圆盘区域内。

公式2令Ω（η，r）表示在复平面上任意以η为圆心，r为半径的圆盘，η，r为实数并且r＞0。则系统（2）A+ΔA中所有特征值分布于圆盘Ω（η，r）内的条件是当且仅当存在正定矩阵P2＞0满足

可以看出不等式（3）（4）关于变量P1和P2不是凸的。为了便于处理该非线性凸矩阵不等式系统的可行性问题，可通过寻找一个公共的李雅普诺夫矩阵来解决问题。即

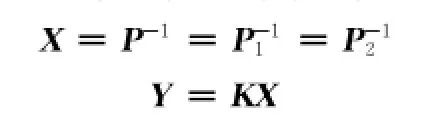
进而给出在范数不确定和扰动存在条件下，对于给定的系统（2），满足极点配置要求的鲁棒控制器存在条件

对于给定的系统（2），若已知量η，r为实数并且r＞0，且存在正定矩阵X＞0和矩阵Y具备适当维数，当满足下列线性矩阵不等式组时：

则存在适当的控制器使得系统渐进稳定的同时将极点配置到指定的区域Ω（η，r）内。

状态反馈控制律的表达式为

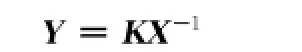
同时保证

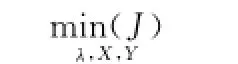
设（γ*，X*，Y*）是该优化问题的最优解，则状态控制律

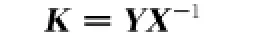
能够保证闭环系统的极点均分布在指定的区域中，并且满足Tωz（s）∞＜γ。

3　数字仿真

以巡航状态下吸气式高超音速飞行器为例，分析其在扰动和范数有界不确定性存在的条件下纵向运动系统的控制鲁棒性能。

设飞行器在V0=15 060ft/s，h0=110 000ft，

γ0=0rad ，q0=0rad/s，α0=0.031 5rad 的平衡条件下巡航。

极点配置的圆盘范围为Ω=（-8，10）且不确定量ΔA= LN（t）E，其中

L=［0.10.10.10.10.1］T

E=［0.10.10.10.10.1］

其中，矩阵L和E为具备适当维数的已知矩阵，反映了不确定参数的结构信息。此外，控制器的关键还有选择加权矩阵Q和R。一般Q选择的越大，系统达到稳态所需要的时间越短；而同样减少R，系统达到稳态所需要的时间也越短。在兼顾超调量、稳态值以及过渡时间和上升时间的基础上，经过仿真选取最优的Q=0.01I，R=0.0001I，求得线性二次型最优反馈矩阵为

K=

且最小的H∞指标γ=5.4144。

图2　闭环系统极点分布图

由上图可知，闭环系统的极点均分布在指定的圆盘Ω=（-8，10）内。

速度和攻角的响应曲线图如图3～4所示。

图3　速度响应曲线图

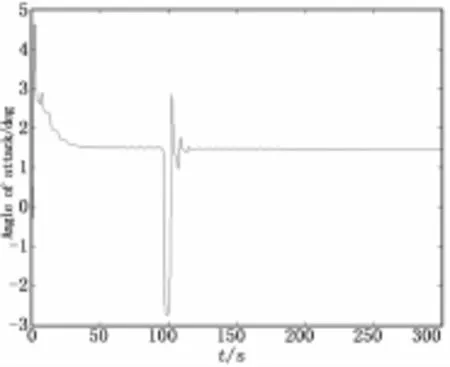
图4　攻角响应曲线图

由上图可知，设计的控制系统可以在不确定性存在的条件下，使闭环系统的状态响应在约110秒内达到稳定状态。

为了对比控制效果，这里同时引用文献［3］中方法，并同时给出仿真结果，如图5所示。分别给出了利用文献［3］方法得到的速度和攻角响应曲线图。

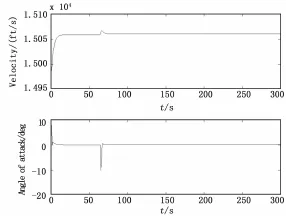
图5　文献［3］中控制器输出响应曲线图

对比可知，文献［3］中设计的控制器在不确定性影响下，系统输出响应曲线虽然能最终收敛到平衡状态，但由于攻角变化剧烈，其取值范围超出了冲压发动机的工作要求范围，最终将导致冲压发动机熄火而停止工作。

可见本文设计的考虑极点配置的基于鲁棒控制的最优控制器，不仅使得闭环系统具有很强的抗模型误差的能力，也增强了对外界的扰动抑制能力，是一种可行的现代控制手段。

4　小结

通过对高超音速飞行器不确定性分析，研究了具有范数有界不确定性的系统，设计了考虑极点配置的基于鲁棒控制的最优控制器。进一步分解为多目标问题，从而将控制器的设计问题转化为具有凸优化约束的线性矩阵不等式的可行性问题，进而利用线性矩阵不等式方法求解。在扰动和不确定性条件下对控制器进行了仿真分析，并与文献［3］中的控制方法进行了比较，结果表明本文设计的鲁棒控制方法能够很好地保证在扰动和不确定性情况下高超音速飞行器控制系统的稳定性能。

［1］罗熊，孙增圻，周贤伟，临近空间高超声速飞行器控制理论和方法的研究现状与发展［A］国防空天信息技术前沿论坛［C］. 2010，1-7.

［2］郭访社，于云峰，龚宇迪.基于LMI的高超鲁棒控制及仿真［J］.计算机仿真，2009，26（2）：65-88.

［3］Gao H，Si Y，Li H，et al.Modeling and control of an air-breathing hypersonic vehicle［A］.in Proceedings of the 7th Asian Control Conference［C］.2009，pp.1114-1119.

［4］Borges R A，Oliveira R C L F，Abdallah C T，et al，H∞filtering for discrete-time linear systems with bounded time-varying parameters［J］.Signal Processing 90（1）（2010），pp .282291.

［5］Basin M V，Shi P，Calderon-Alvarez D，et al.Central suboptimal H∞filter design for linear time-varying systems with state or measurement delay［J］.Circuits Systems and Signal Processing 28（2）（2009），pp .305-330.

［6］Gao Z，Jiang B，Shi P，et al.Passive fault-tolerant control design for near-space hypersonic vehicle dynamical system［J］.Circuits，Systems and Signal Processing，2012，31（4）：565-581.

［7］Wan J，Wang Q，Ai J，Dynamic inversion based control system of a hypersonic vehicle withmodel uncertainty［C］.France，AIAA 2012-5969，2012.

［8］魏毅寅，刘鹏，张冬青，等.国高超声速技术发展及飞行试验情况分析［J］.飞航导弹，2010 （5）：2-9.

［9］Dong C，Hou Y，Zhang Y，et al.Model reference adaptive switching control of a linearized hypersonic flight vehicle model with actuator saturation［J］.Proceedings of the Institution of Mechanical Engineers，Part I：Journal of Systems and Control Engineering，2010，224：289-303.

Design of Robust Controller for Hypersonic Flight Vehicles

Zhang Xue1，Yue Limin2，Liang Xiaogeng1
（1.China Airborne Missile Academy，Luoyang 471009，China；2.Zhengzhou Railway Vocatgional&Technical College，Zhengzhou 450052，China）

The new changes in military innovation and information battlefield make the air-space incorporation battle into one of main future battles.The arriving of Air-breathing Hypersonic Flight Vehicles（AHFV）will give a shock to the traditional offensive and defensive systems.Considering the complex environments，a design of robust and performance oriented control system is the key issue of AHFV.This paper proposes a new methodology，which taking into account the problems of uncertainty and disturbances，to design a robust controller for A HFV.With bounds on the uncertainties，a feedback stabilization problem is converted to an optimal control problem with the demand of pole placement.The contrasts of simulation results indicate that the proposed control law has a good performance and the stability and performance of system can be guaranteed.

hypersonic flight vehicle；robust control；linear matrix inequality；pole placement

1671-4598（2016）05-0077-04

10.16526/j.cnki.11-4762/tp.2016.05.023

TN21

A

2015-10-18；

2015-12-24。

张雪（1984-），女，河北承德人，博士，主要从事红外探测、鲁棒控制等方向的研究。