高中数学数列中数学思想分析
2016-11-22陈芸
陈芸
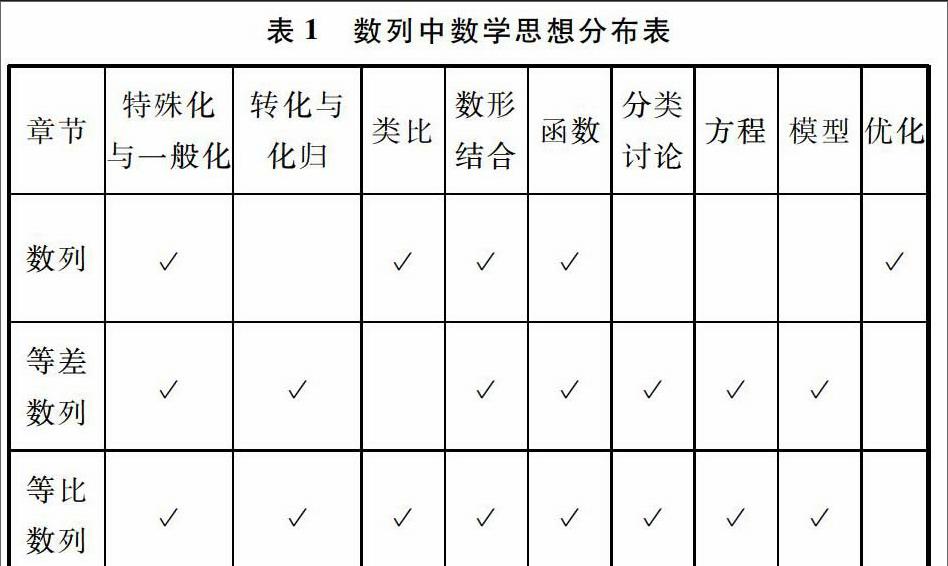
高中数学教学目标之一就是培养学生数学思想,促进学生全面发展.笔者以苏教版教材为载体,选取高中数学“数列”章节,分析数列实例中蕴含的数学思想(表1),说明数学教学与数学思想的内在关联.
笔者在本文就数列中的函数思想、特殊化与一般化思想、类比思想、分类讨论思想、化归思想和模型思想,进行简单介绍与说明,帮助学生更好的理解数列中的数学思想.
一、函数思想
高中数学数列教学以函数思想为指导思想,让学生认识函数和数列之间的关系,强调数列项的排序为函数自变量.从苏教版教材中对数列概念、等差数列与等比数列运算等介绍均体现了函数思想,如数列是正整数集,以一系列离散点为图像,数列通项公式为对应函数解析式.等差数列为一次函数,等差数列前n项和为关于n的二次函数(常数项=0);等比数列为指数函数.数列具有函数一般性质.
二、特殊化与一般化思想
数列章节中关于数列、等差数列、等比数列概念的引出,先给出教学特例,引导学生从特殊中归纳总结一般,得出概念,然后在概念的基础上,应用概念解决问题.另外,等差数列通项公式和求和公式、等比数列通项公式和求和公式的推导,也是从特殊到一般,再从一般到特殊的数学思想.
三、类比思想
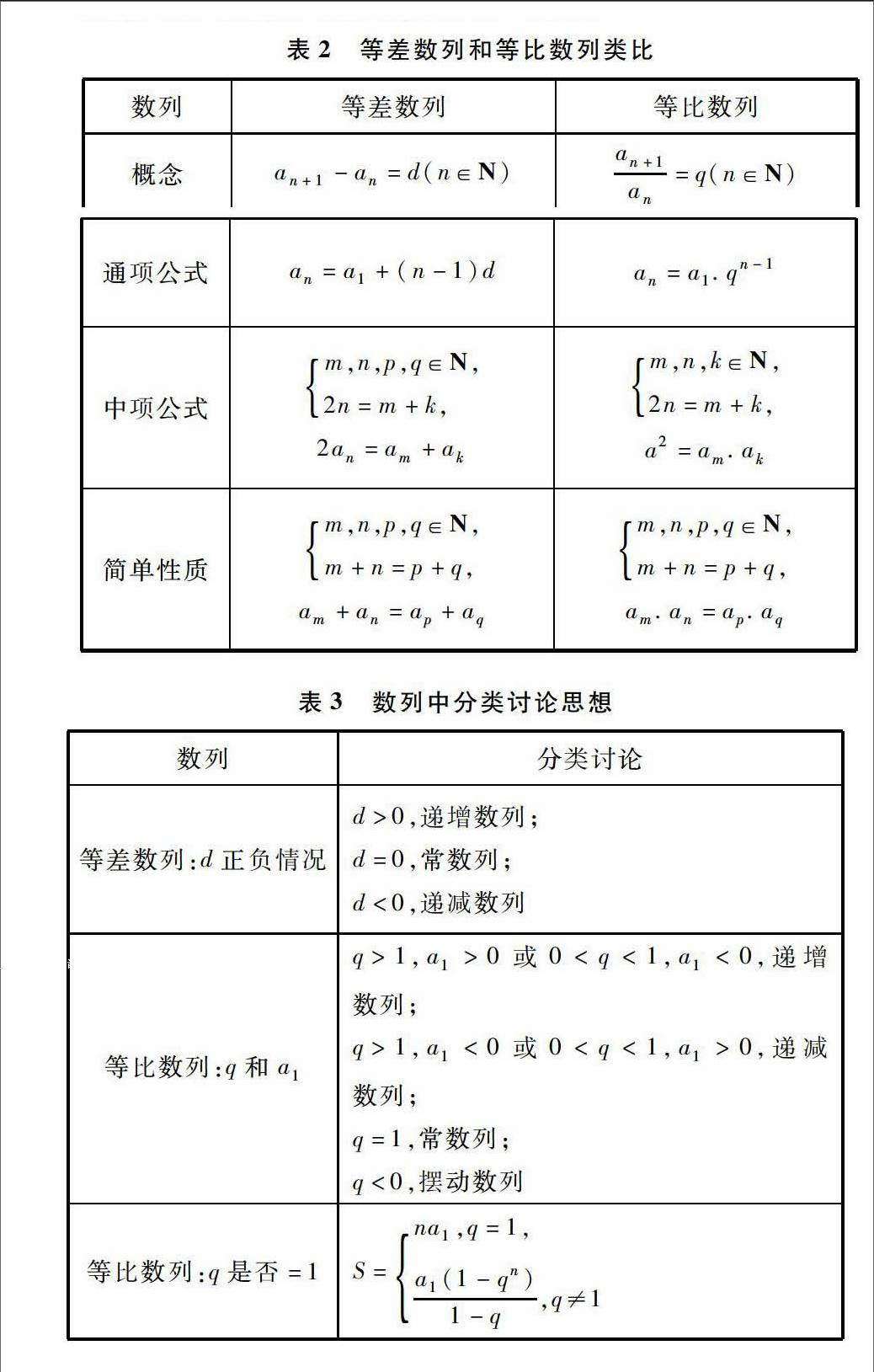
数列章节中等差数列和等比数列的相关内容都是函数类比得出的,如等差数列、等比数列是数列项类比于实数的加法、乘法.等差数列概念、通项公式、前n项和、性质等,类比后得出等比数列特征.数列、等差数列、等比数列等相关问题,可以类比函数概念、表示方法、性质得出.笔者梳理等差数列和等比数列的类比,如表2所示:
四、分类讨论思想
在等差数列和等比数列中均有分类讨论思想的体现,如等差数列中,结合公差d的正负情况分为不同数列;在等比数列中,结合公比q和首项a1范围进行数列分类;等比数列前n项求和Sn,可以结合公比q进行分类讨论,具体如表3所示:
五、化归思想
因为学过等差数列和等比数列前n项和,因此对于一般数列求和,应尽可能将其化归为等差数列或等比数列,然后再求和,体现了数列中的化归思想.
六、模型思想
数列作为离散函数的数学模型,在日常生活中,具体表现为资产折旧、购买贷款、存款利息等问题,利用数列模型思想就可以解决实际问题.
在高中数学教学中,我们应深挖教材中的数学思想,以具体的案例说明数学思想,以数学思想指导数学教学,让数学问题变得简单直观.笔者结合苏教版数列章节知识点,剖析数学思想,为学生呈现教材中案例,及其中蕴含的数学思想,在讲述数列知识点的同时,灵活应用数学思想,转化数列问题,构建与实施高效数学教学课堂.
