自适应混合布谷鸟算法在水电站调度中的应用
2016-11-22李笑竹陈志军樊小朝闫学勤
李笑竹,陈志军,樊小朝,闫学勤
(新疆大学电气工程学院,新疆乌鲁木齐830047)
自适应混合布谷鸟算法在水电站调度中的应用
李笑竹,陈志军,樊小朝,闫学勤
(新疆大学电气工程学院,新疆乌鲁木齐830047)
针对布谷鸟算法局部搜索能力较弱,搜索质量不高的缺点,在标准布谷鸟算法中加入自适应步长策略、边界变异策略,并与模拟退火算法结合成自适应混合布谷鸟算法。经测试函数验证,自适应混合布谷鸟算法与标准布谷鸟算法相比有结果更优,收敛速度更快的优点。将自适应混合布谷鸟算法引入水电站的调度中,通过新疆玛纳斯一级电站验证了该算法的可行性,为求解水电厂优化调度模型提供了一种新思路。
自适应混合布谷鸟算法;模拟退火算法;水电站;优化调度
0 前 言
伴随着我国“十三大水电基地”的规划与陆续建立,中国已形成了世界上规模最为庞大的互联水电系统。中国的水电总装机容量从2004年的1亿kW到2010年的2亿kW,再到2013年突破2.8亿kW,已经稳居世界水电装机量首位,预计2020年将达到4.2亿kW。水电厂系统规模的不断扩大,加剧了水电站优化调度的求解困难。传统的调度模型求解算法存在着各自的缺点,如线性规划、动态规划的求解时间过长[1];粒子群算法[2],遗传算法[3]计算复杂、接近全局最优解时不易收敛,容易陷入局部最优解。
布谷鸟搜索算法[4](cuckoo search,CS),与传统智能搜索算法相比具有参数少、易实现、操作简单、寻优能力强等优点,被广泛应用于各类工程。但是,水电厂的优化调度模型具有高维度,多约束,非线性的特点,标准的布谷鸟算法在求解此类问题时极易陷入局部最优解。本文针对水电站优化调度模型的特点,对标准布谷鸟算法进行改进,引入边界变异策略与自适应步长策略,并将其与模拟退火算法[5]结合形成自适应混合布谷鸟算法(ACS-SA),并用于求解水电站优化调度问题中,为水电站优化调度问题求解提供了一种新思路。
1 水电站优化调度数学模型
水电站的优化调度模型以国家能源发展规划确定的水电发展目标为要求,以灌溉、生态环境保护为约束条件,合理安排水电站各个月份的出力,使水电站内总发电量或总发电效益最大[6]。水电站的优化调度模型包括目标函数和约束条件,本文选取发电量最大作为目标,该数学模型见图1所示。
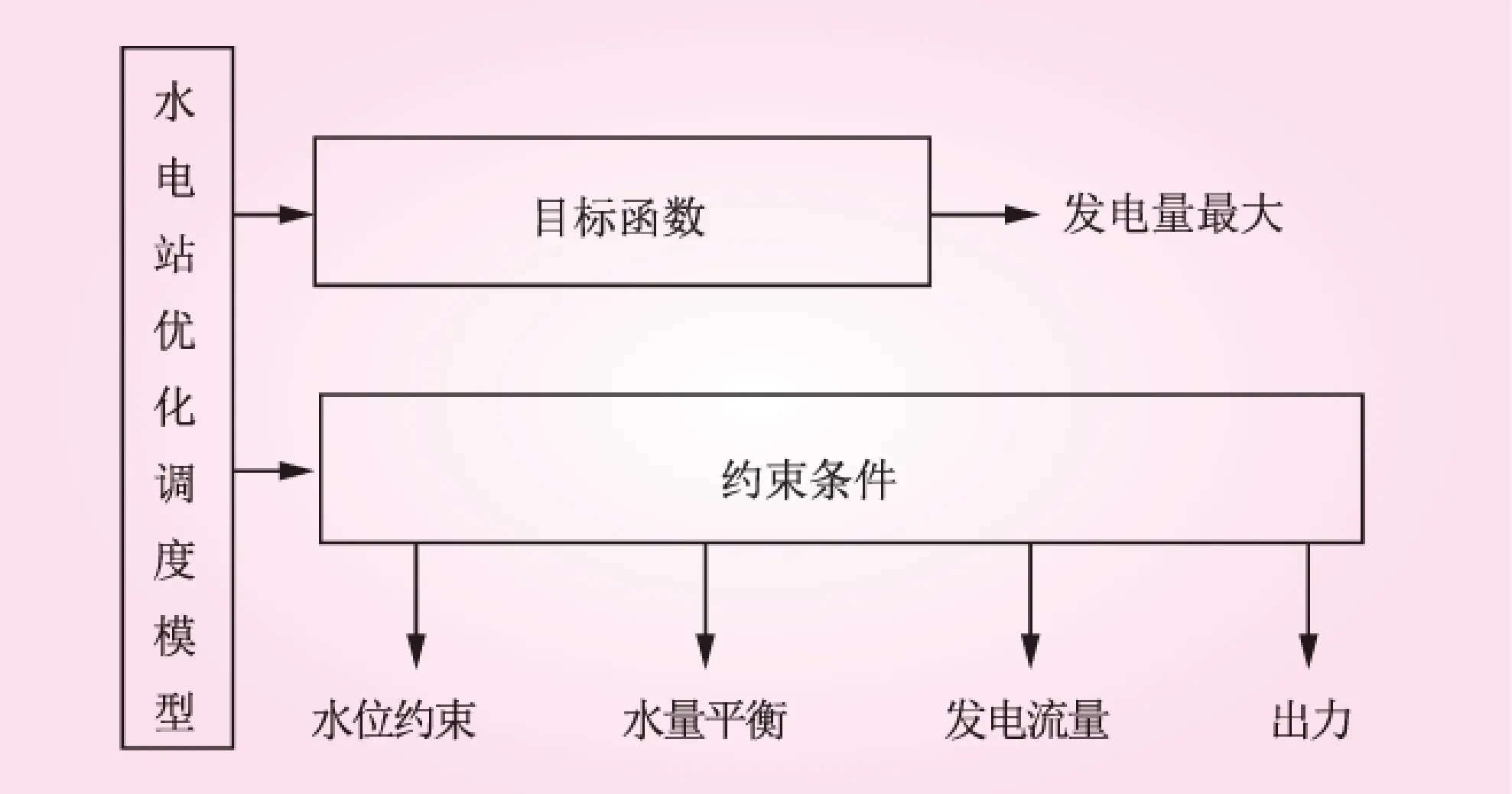
图1 水电厂优化调度数学模型
1.1 目标函数
(1)
式中,E为调度期的总发电量,kW·h;A为该水电站出力系数;Mi为该时段时长,h;Qi为第i时段内的平均发电流量;Hi为第i时段内的平均水头,m。
1.2 约束条件
(1)水位约束
(2)

(2)水量平衡约束。下一时段初蓄水量等于上一时段末蓄水量加来水量减发电用水量和弃水量
Vi+1=Vi+(Qini-Qgeni-Qdisi)Mi
(3)
式中,Qini为第i时段平均入库流量,m3/s;Qgeni为第i时段的平均发电流量,m3/s;Qdisi为第i时段的平均弃水流量,m3/s;Vi第i时段初水库的蓄水量,m3。
(3)发电流量约束
(4)
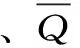
(4)出力约束。出力约束受电站机组的特性以及电力系统的要求限制。即
Nmin≤AQiHi≤Nmax
(5)
式中,Nmin电力系统要求的最小出力,kW;Nmax电力系统要求的最大出力,kW。
2 自适应混合布谷鸟算法
2.1 标准布谷鸟算法
布谷鸟搜索算法是由剑桥大学YANG等提出的一种群智能优化算法,它也是一种(新型元)启发式搜索算法,其主要思想基于两个策略:布谷鸟的巢寄生性和莱维飞行机制[4]。布谷鸟本身没有孵化行为,在繁殖期将卵产在宿主鸟窝里让其孵化。当卵被发现,布谷鸟则要重新寻找宿主鸟窝。该新巢替换旧巢的概率可以用Pa表示。布谷鸟通过随机游走的方式即莱维飞行搜索到一个最优的鸟窝孵化鸟蛋,该方式是一种高效的寻优模式。
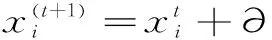
(6)
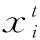
式中,λ是常量。
综上所述,布谷鸟算法的算法步骤描述如下:
(1)定义目标函数f(x),初始化函数,随机生成n个鸟巢的初始位置。设置种群规模、最大迭代次数、最小误差要求、维数、发现概率Pa。
(2)计算每个鸟巢的目标函数值,找出当前最优函数值。
(3)记录上一代最优函数值,利用更新公式更新下一代鸟巢位置。
(4)找出现有函数最优值与上一代最优值比较,若较好,则改变当前最优值。
为高效构建云南特色电力大数据中心,云南电网公司以开源技术为基础,构建了云南电网第一个集云计算、大数据为一体的智能型“云电智云”平台,为云南电网用户提供云计算和大数据服务。这是南方电网首个通过入网安评测试的集大数据、云计算为一体的智能云平台,在全国央企行业的云计算、大数据应用方面处于前列。
(5)用随机数γ∈[0,1]与Pa比较,若γ>Pa,则对鸟巢进行随机改变,反之不变。最后保留最好一组鸟巢位置。
(6)未达到最大迭代次数或最小误差要求则继续迭代。
(7)输出全局最优解。
2.2 自适应混合布谷鸟算法(ACS-SA)
2.2.1 边界变异策略
在优化过程中,当某个鸟巢超出了可行范围 [Xmin,Xmax],标准的布谷鸟算法会将其鸟巢强行拉回边界上,让xi=Xmax或xi=Xmin。但聚集到边界上的解过多,不利于算法的收敛,出现标准算法到后期收敛速度慢的缺陷。
因此,本文对每一代中超出边界的鸟巢进行越界处理,避免聚集到边界上的解过多,以进一步提高鸟巢质量,变异策略如下
当xi>Xmax时,
(7)
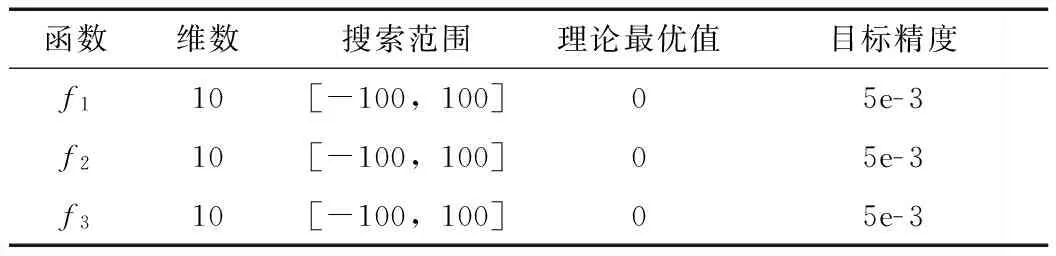
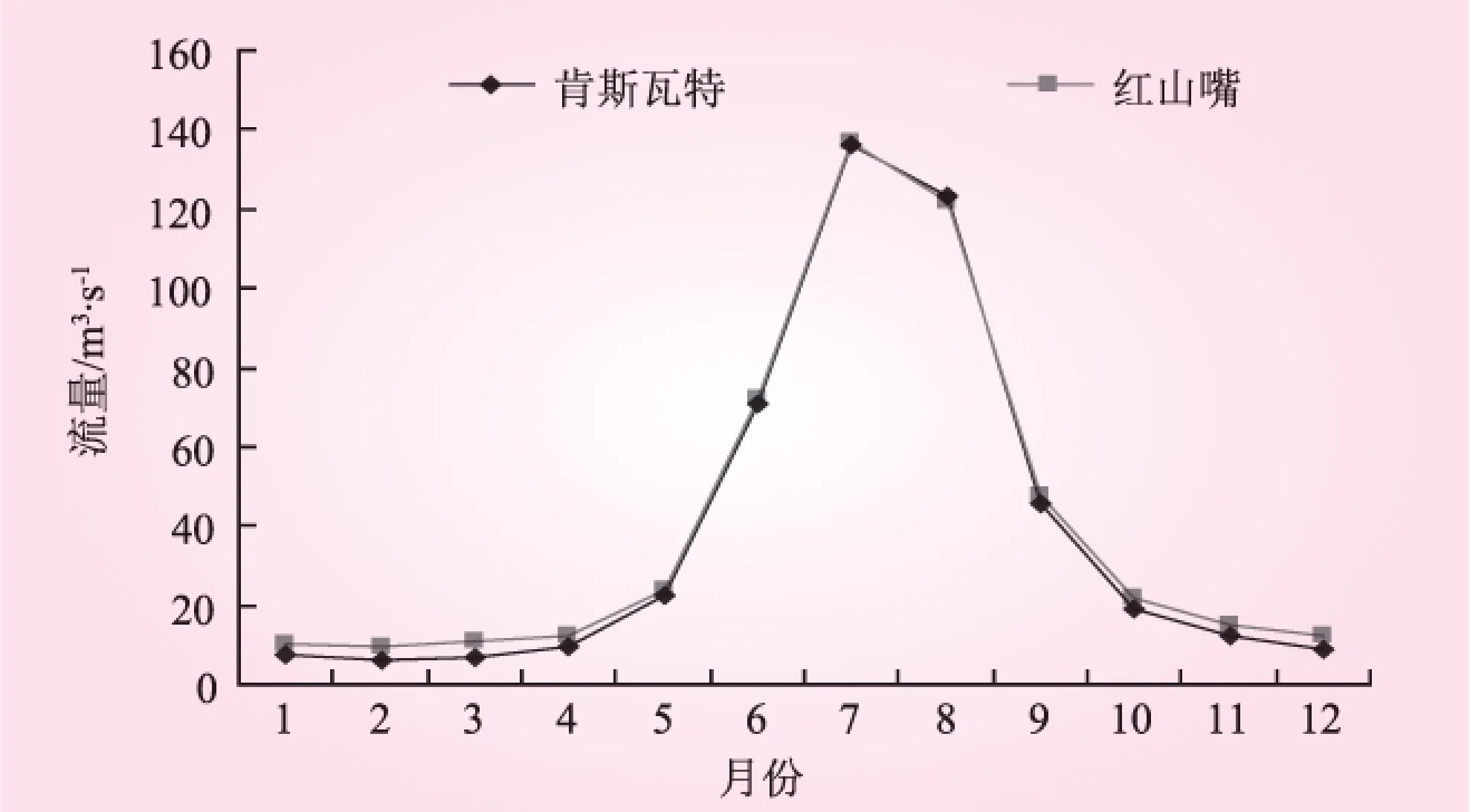
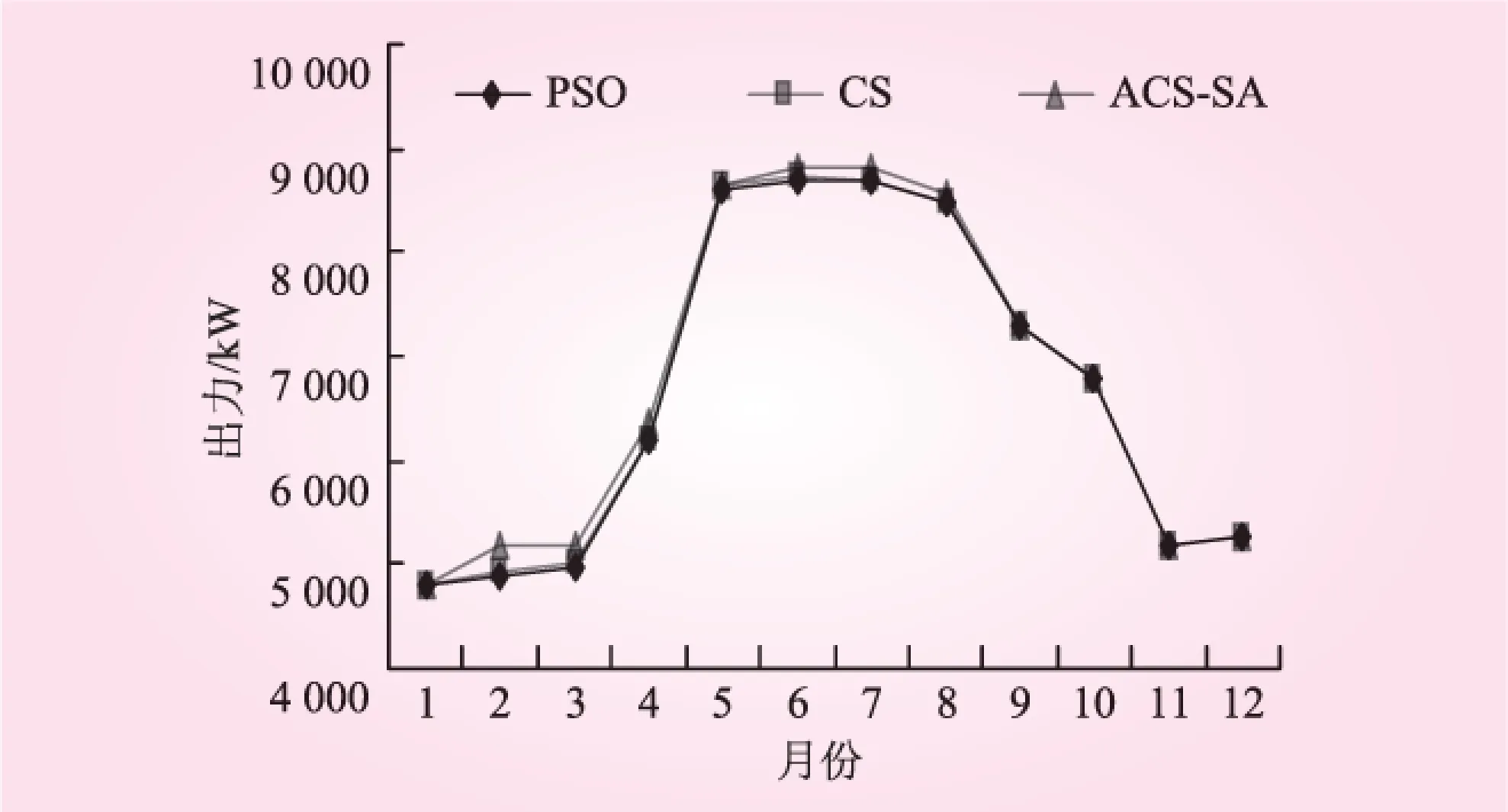
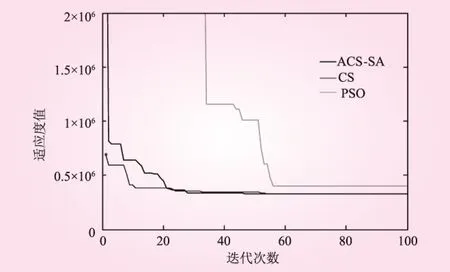
当xi (8) 式中,rand为0到1之间的随机数;c为设定的参数。 2.2.2 自适应步长改进 莱维飞行模式在更新下一代鸟巢中,乘以随机步长∂以控制随机搜索,该模式缺乏自适应性。∂如果过大,更新的新鸟巢位置将会落在边界以外;∂如果过小,无效搜索,新一代的解与原先的解差别不大。 因此,在本文中随机步长∂被修改如下: (9) 式中,αL与αu分别是定义的最小和最大步长;Fj为j鸟巢的适应度值;Fmin与Favg是一代中所有鸟巢适应度值的最小值和平均值。布谷鸟从当前优解附近寻找鸟巢,因为这些区域被视为高存活区,即可能包含最优解地区。反之,布谷鸟在死亡区进行更为严格的搜索。通过多次试验αL和αu分别为1和5。 2.2.2 混合布谷鸟算法 布谷鸟搜索算法存在局部搜索能力较弱的缺点,为了提高局部搜索能力,将模拟退火算法与布谷鸟算法合并,从而改进计算结果的准确度。模拟退火算法是模拟固体退火降温的过程,在加热固体过程中,固体的热运动不断增强,内能增大,内部粒子随温度的升高呈无序状。冷却时,粒子内能逐渐降低,在每个温度下达到平衡状态,最后在常温下达到最终平衡,此时内能也减为最小。 在实际应用中,我们可将内能E模拟为目标函数值f,将温度T模拟为控制参数,从一给定解开始,从该解某一领域随机产生一个新解,利用接受准则判断接受或舍弃新解,算法持续进行“产生新解—计算目标函数差—判断是否接受新解—接受或舍弃”的迭代过程。经大量解变化后,得到给定控制参数T值时的相对最优解,然后减小控制参数T,重复上述迭代过程。ACS-SA算法流程图见图2。 图2 算法流程 2.3 数值验证ACS-SA高效性 为了测试本文提出的自适应混合布谷鸟算法的性能,采取3个标准测试函数对算法经行检验。测试函数参数如表1所示。 (10) 表1 测试函数参数 函数维数搜索范围理论最优值目标精度f110[-100,100]05e-3f210[-100,100]05e-3f310[-100,100]05e-3 将标准布谷鸟算法与自适应混合布谷鸟算法进行对比测试,其中试验参数设置如下:种群规模均为N=50;发现概率Pa=0.25。实验对每个测试函数经行50次独立运算,对迭代次数、4.23×10-151最优值、最差值、平均值进行对比,计算结果统计如表2。可以看出,自适应混合布谷鸟算法更加接近全局最优解,迭代次数明显减少,寻优质量亦有一定提高。 表2 结果统计 函数理论值最优值最差值平均值合格次数CSACS-SACSACS-SACSACS-SACSACS-SAf103.18×10-74.23×10-1514.21×10-35.43×10-882.47×10-55.43×10-1234350f204.57×10-54.53×10-1375.21×10-73.64×10-653.18×10-74.17×10-1073850f302.58×10-88.1×10-1544.25×10-75.31×10-914.57×10-71.53×10-1344150 3.1 应用背景 玛纳斯河是新疆天山北坡经济带中最大的一条河流,水力蕴藏量为59万kW。红山嘴电厂位于新疆北部准葛尔盆地边缘,玛纳斯河流域中游,始建于1961年,是新疆开发建设最早的水电厂之一。红山嘴电厂共规划了是11个梯级水电站,其中水库式电站4个,引水式电站7个。其中玛纳斯一级电站(装机4万kW,引用流量49.7 m3/s,水头97 m,)[7],位于红山嘴电厂最上游,该电站的运行调度与下游电站的是否能顺畅衔接,安全运行有很大关系。因此,本文以玛纳斯一级电站为例经行优化调度仿真计算。玛纳斯河季节性非常强,平均径流量12.5 m3/s,单年内径流变化很大,丰水期与枯水期月平均径流量相差10倍以上,流量统计见图3。 图3 玛纳斯河流量统计 3.2 结果比较 为了验证算法有效性,本文分别采用粒子群算法(PSO)、标准布谷鸟算法(CS)、自适应混合布谷鸟算法(ACS-SA)进行求解。算法参数设置如下:种群规模均为N=50;最大迭代次IterTotel=100,发现概率Pa=0.25。经过计算,得到水电站调度期的出力过程,如图4所示。3种计算方法的收敛过程如图5所示。 图4 出力对比 图4为水电站出力每月变化过程,三种算法比较接近,但自适应混合布谷鸟算法在2~4月、6~8月比其他两种算法多。 图5 收敛过程对比 从图6可以看出自适应混合布谷鸟算法较其他两种算法有收敛速度快、寻优时间短的优点,同时寻优结果也更加稳定。 (1)将自适应布谷鸟算法与模拟退火算法结合,有效避免了在求解过程中容易陷入局部最优解的缺点,并且进一步提高了算法的收敛速度使寻优结果更加准确、稳定。 (2)将自适应混合布谷鸟算法引入水电站优化调度中,为水电站优化调度模型求解提出了一种新思路,并用实例结果验证了本文方法在水电站优化调度的可行性与实用性。 (3)尝试了自适应混合布谷鸟算法在水电站调度中的初步探索,今后可进一步研究求解梯级水电站群或混联水电站群的联合优化调度问题。 [1]郭生练, 陈炯宏, 刘攀, 等. 水库群联合优化调度研究进展与展望[J]. 水科学进展, 2010(4): 496- 503.[2]黎晓峰, 薛保菊, 李维乾. 基于改进粒子群算法的水库优化调度研究[J]. 水力发电, 2008, 34(11): 107- 109. [3]钟平安, 徐斌, 张金花. 水电站发电优化调度遗传算法的改进[J]. 水力发电学报, 2011(5): 55- 60. [4]兰少峰, 刘升. 布谷鸟搜索算法研究综述[J]. 计算机工程与设计, 2015(4): 1063- 1067. [5]张永永, 黄强, 畅建霞. 基于模拟退火遗传算法的水电站优化调度研究[J]. 水电能源科学. 2007(6): 102- 104. [6]张睿. 流域大规模梯级电站群协同发电优化调度研究[D]. 武汉: 华中科技大学, 2014. [7]刘新鹏, 钟久晞. 新疆玛纳斯河一级水电站建设中的若干重要问题[J]. 中国水能及电气化, 2008(Z1): 69- 75, 93. (责任编辑 高 瑜) Application of Adaptive Hybrid Cuckoo Algorithm in the Operation Dispatching of Hydropower Station LI Xiaozhu, CHEN Zhijun, FAN Xiaochao, YAN Xueqin (College of Electrical Engineering, Xinjiang University, Urumqi 830047, Xinjiang, China) An adaptive hybrid cuckoo algorithm is developed to alleviate the defects of standard cuckoo algorithm, such as premature convergence and poor search ability, in which, the boundary mutation strategy in process of evolution algorithm and adaptive step adjustment strategy to improve the standard algorithm are used, and the simulated annealing algorithm is also combined into adaptive hybrid cuckoo algorithm. The new algorithm has been verified by test function, and the results show that the adaptive hybrid cuckoo algorithm can achieve better result and fast convergence speed when comparing with standard cuckoo algorithm. This new algorithm is introduced to the optimal operation of hydropower station. The application of new algorithm in Manas I Hydropower Station verifies the feasibility of method, which provides a new way for solving hydropower optimal operation model. adaptive hybrid cuckoo algorithm; simulated annealing algorithm; hydropower station; optimal operation 2016- 02- 20 国家自然科学基金项目(51106132);新疆维吾尔自治区自然科学基金(2015211C272) 李笑竹(1990—),女,新疆昌吉人,硕士研究生,研究方向为智能算法数据驱动;陈志军(通讯作者). TK89 B 0559- 9342(2016)06- 0070- 04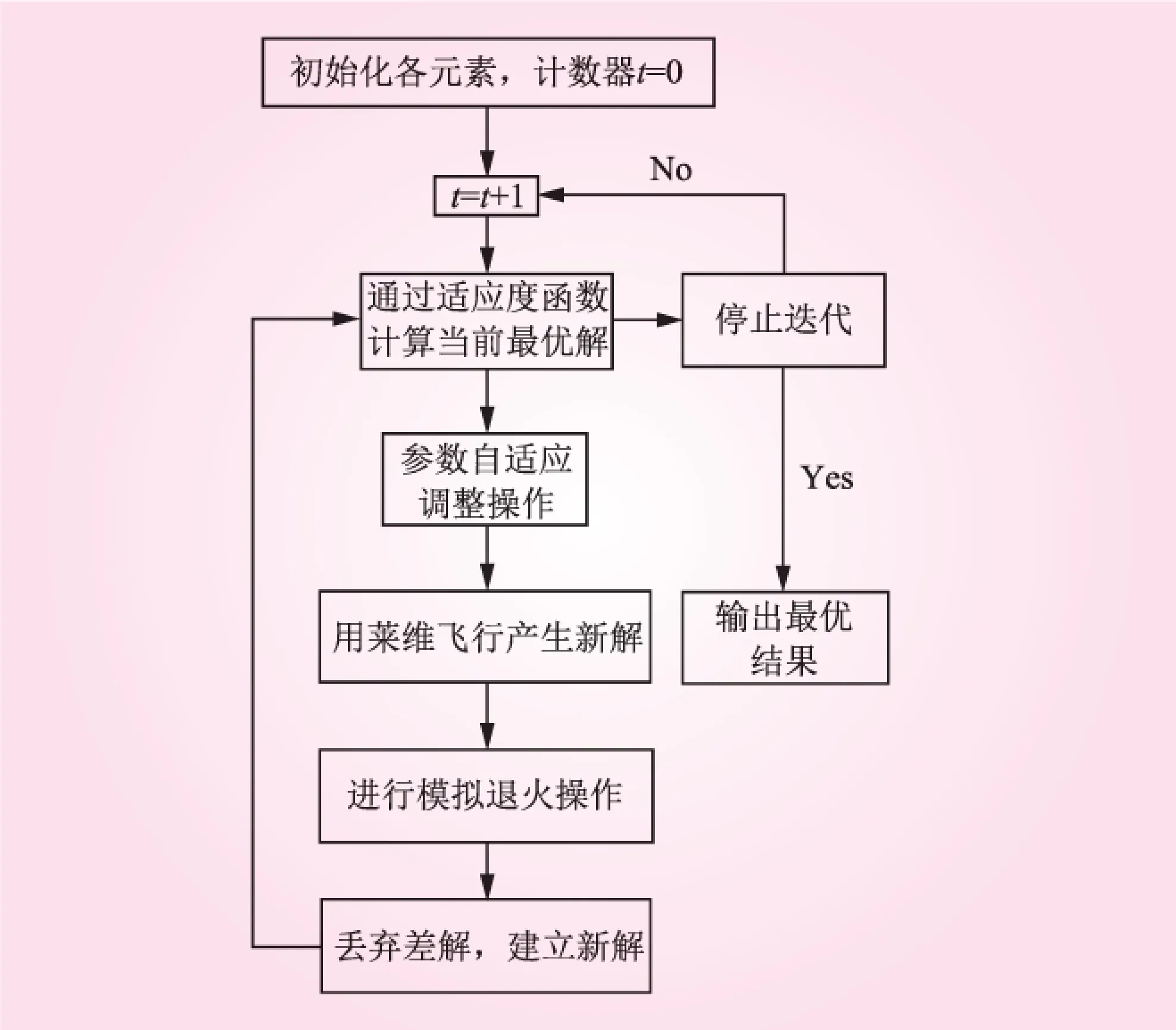

3 工程应用
4 结论与展望
