基于降雨分布不均匀性的空间插值方法适用性研究

郭卫国，陈 喜，张润润

( 1.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京210098；2.河海大学水文水资源学院，江苏南京210098)



基于降雨分布不均匀性的空间插值方法适用性研究

郭卫国1，2，陈 喜1，2，张润润1，2

( 1.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京210098；2.河海大学水文水资源学院，江苏南京210098)

为定量评估降雨空间分布不均匀程度，以史灌河流域为研究区选取48个雨量站1998年到1999年92场日降雨观测资料，首次提出降雨空间集中度概念，分析降雨空间集中度与面平均雨量、插值误差的关系。采用反距离权重法、局部多项式法、径向基函数法、普通克里金法以及协同克里金法对拟定的站点进行空间插值，并用相对平均误差评判插值结果的好坏，分析不同降雨空间分布下各种插值方法的优劣。

降雨插值；降雨空间集中度；方法比较；相对平均误差

0 引 言

降雨空间分布信息及面雨量估算一直以来都是区域气象学、水文学、水资源学、生态学等学科的重要研究内容。影响降雨空间分布的因素很多，如气象站点位置、高程、坡向、坡度以及离水体的距离等[3]。根据雨量站观测雨量进行空间插值是描述雨量空间分布及计算面雨量的重要手段。现有的雨量空间插值方法有很多[4]，通常可分为三类：整体插值法、局部插值法、混合插值法[2]。整体插值法即通过拟合区域上所有已知点实测资料来预测未知点雨量信息，该方法有趋势面法、多元回归法等。局部插值法通过拟合区域上部分已知点实测资料来预测未知点雨量信息，有泰森多边形法、反距离权重法、克里金插值法、径向基函数法等。混合插值法则是通过改正整体插值法中存在的残差来进一步提高插值精度。除以上三类方法外，还有采用人工神经网络技术用于空间插值[7]的方法。

插值精度不仅和插值方法本身结构有关，还与已知点是否能够代表插值变量的空间变化特征及其影响要素(如站点高程、经纬度等)有关[5]。因此，考虑插值变量的空间变化特性与插值方法间的关联尤为重要。本文利用史灌河流域雨量站点密集的观测资料，通过引入降雨空间集中度这一概念，描述降雨在空间上分布的不均匀性，分析降雨空间集中度与面平均雨量、插值误差的关系，定性评价不同降雨空间分布下各种插值方法的优劣。

表1 各插值模型特点[1- 7]

分析插值方法反距离权重法(IDW)局部多项式法(LPI)径向基函数法(RBF)普通克里金法(Kriging)协同克里金法(Cokriging)公式原理插值点与已知点距离作为权重采用(二次)多项式拟合区域上的点数据采用(规则样条)函数拟合区域上的点数据,同时使其表面总曲率最小采用协方差函数或者半变异函数,使得区域化变量的值具有无偏性和最优性采用交叉协方差和交叉半变异函数建模,用此得到区域化变量的无偏和最优估计优点方法只需插值点与已知点的距离,运算速度快,具有普适性,不需要根据数据的特点对方法加以调整方法易于理解,较好反映局部变异,比全局多项式法和克里金法灵活很多为精确插值,并且使插值曲面总曲率最小不仅考虑数据的地理特征,考虑数据的空间相关性和变异性结合其他相关信息,尽可能从海量数据中提取相关信息缺点某些数据与相邻点有显著差异时,插值误差大,不能很好的反映真实曲面插值曲面很少通过原观测点,不是精确插值方法当已知点不能反映插值变量空间变化特性时,插值精度比较差插值曲面通常比真是曲面平滑方法运行时间长,并且当协同变量与插值变量相关性较差时,插值精度并无提高

1 分析方法

1.1 空间插值方法

本文采用了五种插值方法(见表1)，其基本原理和计算方法[1]分述如下。

(1)反距离权重法。反距离权重插值是一种局部方法，它假设未知值的点受较近点的影响比较远控制点的影响更大，如采用距离二次方的倒数作为权重因子，其算式

(1)

式中，di为控制点与预测点的距离；Zi控制点已知值；d*为预测值；n为控制点个数。

(2)局部多项式法。采用多项式模拟空间上已知点降水量分布，以此插值空间上的未知点降水量称为多项式插值法。全局多项式法采用一个多项式拟合区域已知点降水量，局部多项式法采用多个多项式拟合区域已知点降水量，每个多项式都处在特定重叠的临近区域。经过多次交叉验证计算对比分析，本次计算采用局部二次多项式法。

(3)径向基函数法。从概念上来说，径向基函数法如同将一个软膜插入并经过各个已知样点，同时又使表面总曲率最小。径向基函数包括5种不同的基本函数：平面样条函数、张力样条函数、规则样条函数、高次曲面函数和反高次曲面样条函数，选择何种基本函数意味着将以何种方式使径向基表面穿过一系列已知样点。本次计算采用规则样条函数。

(4)普通克里金法。以空间自相关性为基础，设区域化变量二阶平稳或内蕴假设，采用协方差函数或者半变异函数，使得区域化变量的值具有无偏性和最优性，即

(2)

式中，λi为权重系数；Zi为i点的实测值；n为已知点个数。

黄河下游移动式不抢险潜坝的可移动性在于坝体可以拆卸重复使用。预应力管桩作为潜坝的主体，在施工阶段拔桩过程中，桩体主要承受拉力，只有满足抗拉承载力及抗裂条件下，确保构件的安全可靠度，才能够真正实现潜坝的可移动性。

(5)协同克里金法。协同克里金法采用交叉协方差和交叉半变异函数建模，以得到区域化变量的无偏和最优估计。即

(3)

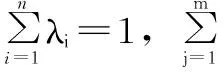
1.2 降雨空间集中度(PC)

降雨空间不均匀性是影响各插值法误差的主要因素。为此，本文引入降雨空间集中度来评定降雨集中的程度。计算方法类似于时间上的降雨集中度[8]，步骤如下：

(1)利用泰森多边形计算各雨量站控制面积，选出插值站点的时段降雨量以及控制面积，并把时段降雨量从小到大排列。

(2)以各站面积累加百分比为横坐标，以面积为权重为纵坐标，计算对应面积权重的降雨累加百分比

(4)

(5)

式中，Ak为第k站的面积；Pk为第k站降雨量；n为总站数，i=1，2，…，n；sum(Ai)为各站面积累加百分比；sum(Pi·Ai)为对应某一面积权重的降雨累加百分比。

(3)点绘sum(Ai)-sum(Pi·Ai)曲线，计算其与sum(Ai)=sum(Pi·Ai)这条直线所围成的面积(见图1)，该面积除以0.5即为这PC。

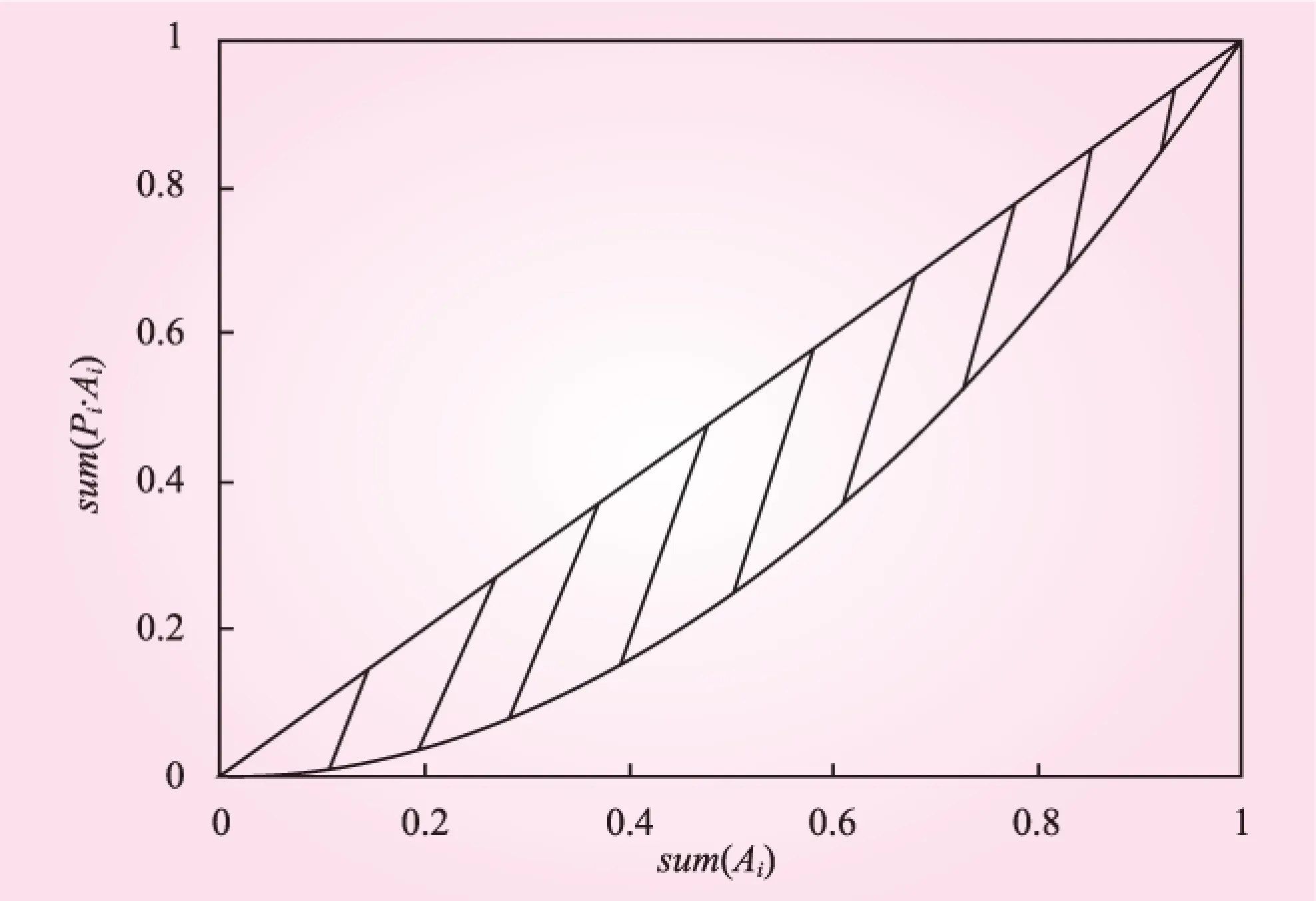
图1 降雨空间集中度计算示意

1.3 插值方法计算精度评估

采用站点实测雨量与插值雨量之间的相对平均误差评判各插值方法的优劣

(6)

式中，Z(ui,k)、Z*(ui,j,k) 分别为对第j场降雨采用第i种插值方法时k站点实测与预测值；MREi,j为对第j场降雨采用第i种插值方法时n个插值站点相对平均误差，i=1，2，…5；j=1，2，…，np。

各插值方法所得面平均雨量相差很小，他们两两之间的相关性系数都在0.98以上，所以可将各插值方法所得面平均雨量的算术平均值设为该流域面平均雨量，即

(7)

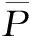
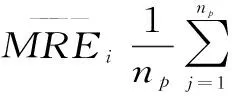
2 插值结果与精度分析

2.1 雨量站点分布及观测数据

史灌河是淮河一级支流，分史河和灌河两个分支，以史河为主干。史灌河发源于安徽省金寨县，流经霍邱县、河南省商城县和固始县，全长211km，集水面积6 889km2，在淮河三河尖水文站处汇入淮河，流域平均海拔254m。流域地处我国南北气候过渡带，气候温和，年平均气温为11～16 ℃，年平均水面蒸发量为900～1 500mm，多年平均降水量约为920mm，冬春干旱少雨，夏秋闷热多雨。

本文选取“淮河流域能量与水分循环试验”加强观测资料，实测降雨站点48个，在加强观测期1998年～1999年中选取92场日降雨观测数据。其中日降雨量最大为195mm，发生在1998年8月16日的全军站；年降雨量最大(1 848mm)发生在西河站，最小值(709mm)发生在杨集站。本文在48个雨量站中选择40个训练集建立插值模型，剩余8个测试集验证插值模型的优劣。

2.2 降雨空间集中度及插值误差的统计分析

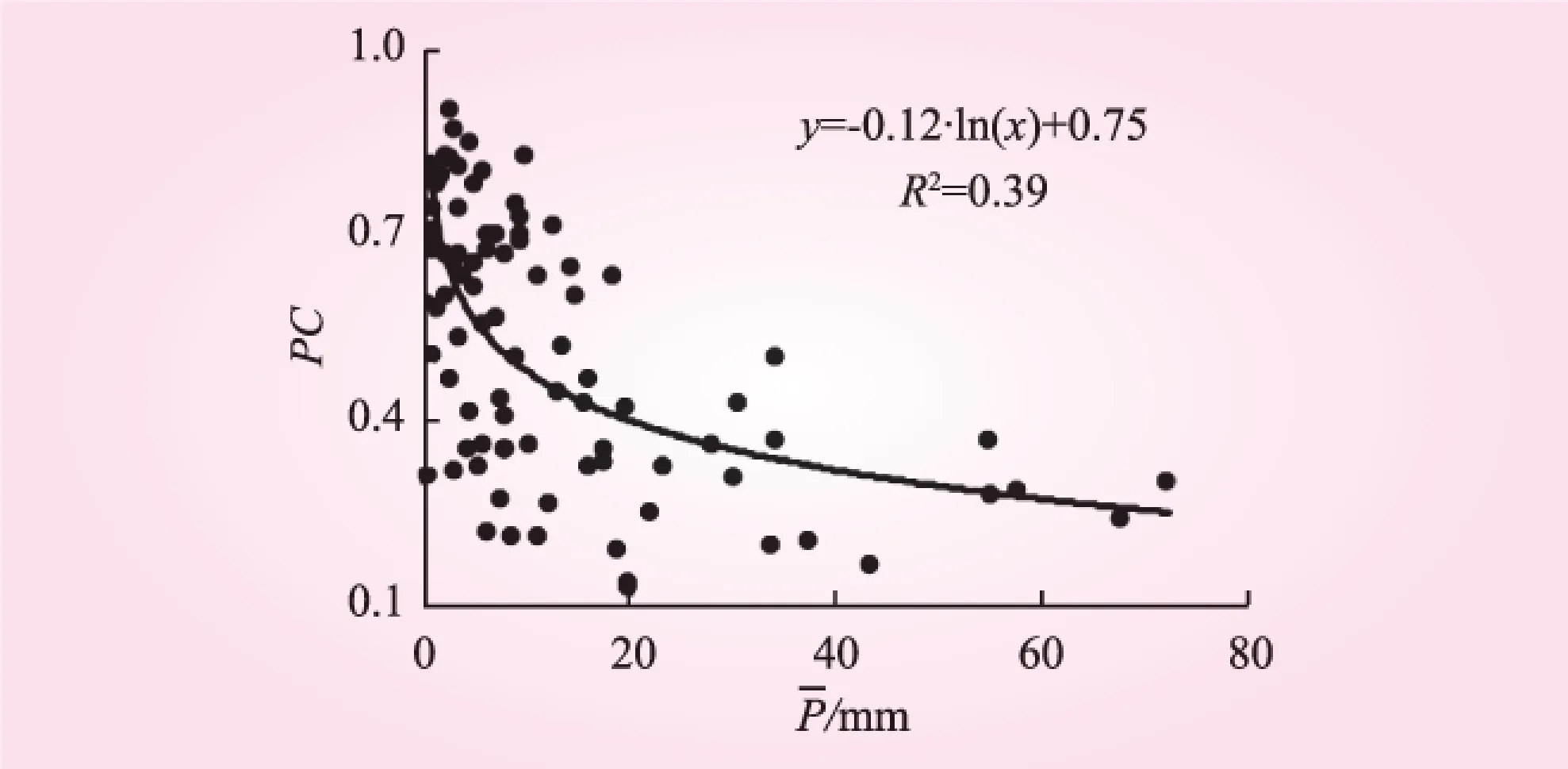
图2 PC与关系

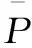
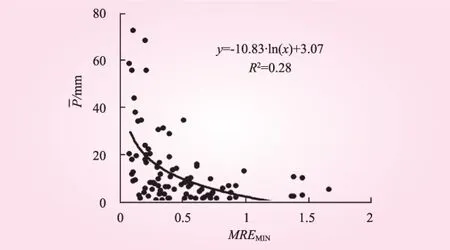
图3 MREMIN与PC关系

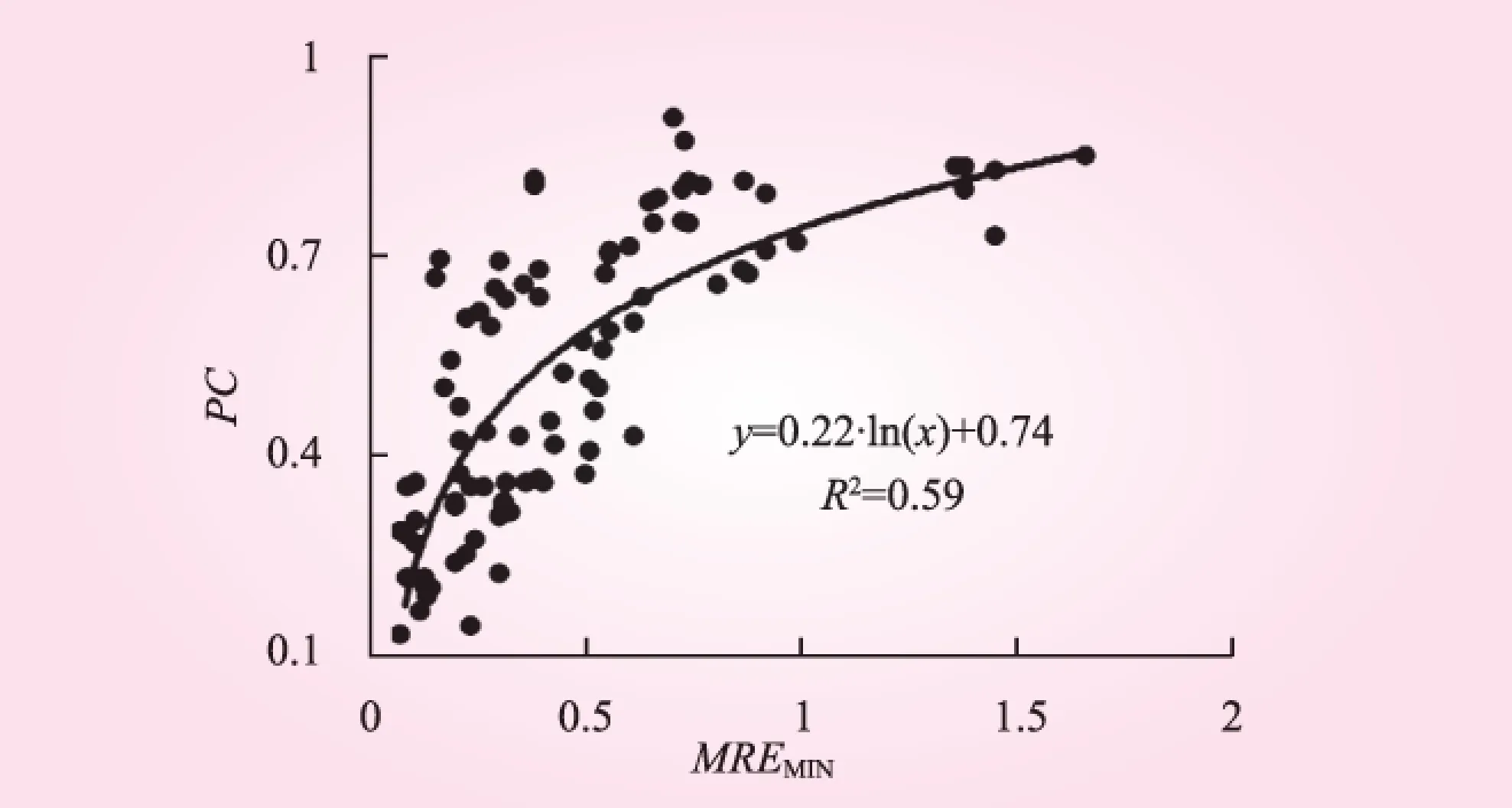
图4 MREMIN与关系

由图2～4得：当面平均雨量小时，局地降雨的集中度大，即降雨分布越不均匀，插值方法推求的雨量误差越大；相反，当面平均雨量大时，全流域降雨集中度小，即降雨分布均匀，由此插值的雨量误差小。

表2 不同插值方法下各参数统计值

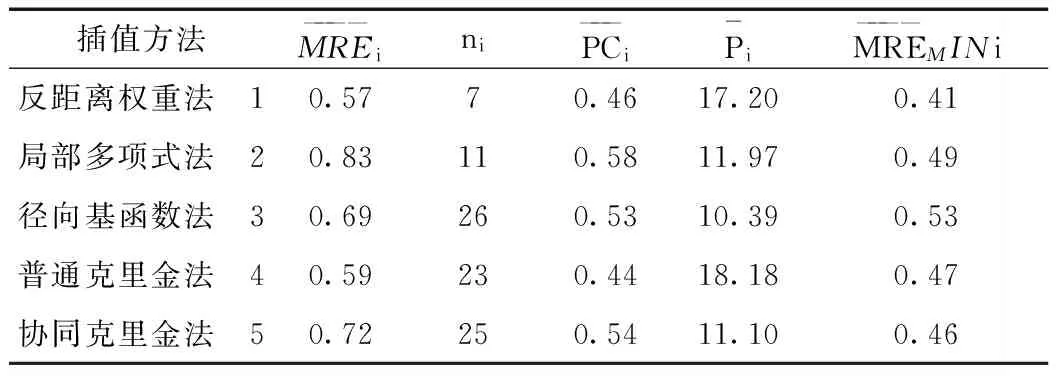
插值方法MRE————iniPC———iP-iMRE————MINi反距离权重法 10.5770.4617.200.41局部多项式法 20.83110.5811.970.49径向基函数法 30.69260.5310.390.53普通克里金法 40.59230.4418.180.47协同克里金法 50.72250.5411.100.46

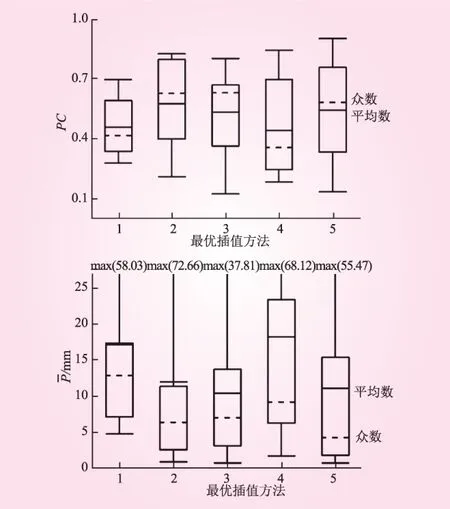
图5 不同最优插值方法下PC和变化的箱形

为进一步分析PC与插值方法的关系，将PC大于0.5的场次降雨与PC小于0.5的场次降雨分别统计分析。由下表3可明显看出空间降雨集中度与插值误差成正比关系、与面平均雨量成反比关系，与前面所得结论一致。结合表2，在考虑被选为最优插值方法次数时，对应于史灌河流域可得以下结论：当PC小于0.5时，方法4更好；当PC大于0.5时，方法3、5更好。

表3 不同插值方法下各参数统计值(PC≤0.5|PC>0.5)

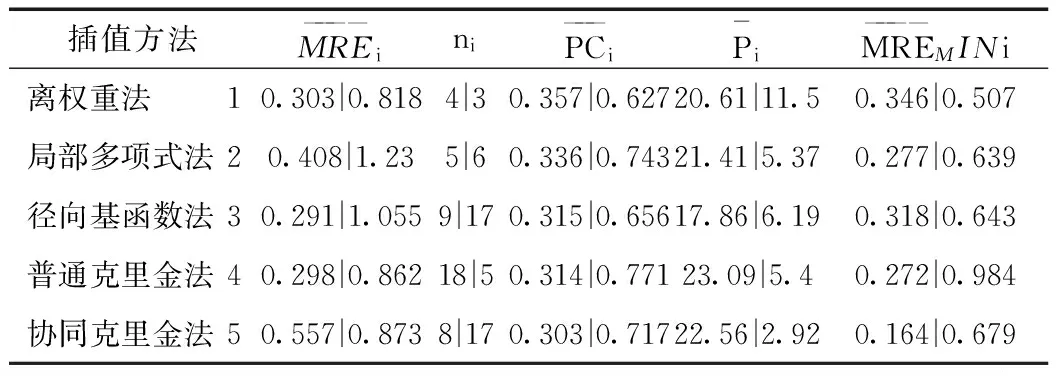
插值方法MRE————iniPC———iP-iMRE————MINi离权重法 10.303|0.8184|30.357|0.62720.61|11.50.346|0.507局部多项式法20.408|1.235|60.336|0.74321.41|5.370.277|0.639径向基函数法30.291|1.0559|170.315|0.65617.86|6.190.318|0.643普通克里金法40.298|0.86218|50.314|0.77123.09|5.40.272|0.984协同克里金法50.557|0.8738|170.303|0.71722.56|2.920.164|0.679

3 结 语

本文构建降雨空间集中度指标，分析史灌河流域48个雨量站92场降雨的空间分布不均匀程度，以及不同降雨空间集中度下插值结果误差的统计特征，对应于史灌河流域有以下结论：

(1)由于流域雨量站点分布密集，各种插值方法所得面平均雨量相差较小。

(2)降雨空间集中度与面平均雨量成反比、与插值误差成正比，即降雨越小，空间分布越不均匀，各种方法插值未知点雨量时误差增大。

(3)相对而言，普通克里金法适用于小的大降雨空间插值，径向基函数法和协同克里金法更适用于大的小降雨空间插值。

(4)与插值模型的精度有一定关系，就史灌河流域而言，当降雨空间不均匀程度小时，考虑距离因素和空间变异性的普通克里金法插值效果较好；当降雨空间不均匀程度大时，考虑协同高程因素的协同克里金法和减弱插值曲面变化的径向基函数法插值效果较好。如何将恰当的引入各降雨插值模型以提高插值精度是一个值得进一步探究的问题。

[1]汤国安， 杨昕. ArcGIS地理信息系统空间分析实验教程[M]. 北京： 科学出版社， 2006： 363- 422.

[2]何红艳， 郭志华， 肖文发， 等. 降水空间插值技术的研究进展[J]. 生态学杂志， 2005， 24 (10)： 1187- 1191.

[3]FEDOROVSKI A. Estimating areal average rainfall for an ungauged mountainous basin in the Amur Basin[J]. Journal of Environment Hydrology， 1998(6)： 5- 15.

[4]LAM N. Spatial interpolation methods： a review[J]. The American Cartographer， 1983， 10(2)： 129- 149.

[5]GOOVAERTS P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall[J]. Journal of Hydrology， 2000， 228(1- 2)： 113- 129．

[6]朱会义， 贾绍凤. 降雨信息空间插值的不确定性分析[J]. 地理科学进展， 2004， 23(2)： 34- 42.

[7]尤淑撑， 严泰来. 基于人工神经网络面插值的方法研究[J]. 测绘学报， 2000， 29(1)： 30- 34.

[8]黄晓亚， 陈喜， 张志才， 等. 西南喀斯特地区降雨集中度及其变化特征分析——以乌江流域中上游为例[J]. 地球与环境， 2013， 41(3)： 203- 208.

(责任编辑 陈 萍)

Study on the Applicability of Spatial Interpolation Methods Based on the Heterogeneity of Rainfall Distribution

GUO Weiguo1,2, CHEN Xi1,2, ZHANG Runrun1,2

(1. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098,Jiangsu, China; 2. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, Jiangsu, China)

In order to quantitatively assess the uneven degree of spatial precipitation distribution, a subbasin of Shiguan River in Huaihe River Basin is selected as study object, and the daily rainfall observation data of total 92 events during 1998- 1999 from 48 rainfall stations are used to analyze the relationship of concentration of spatial precipitation with mean surface rainfall and interpolation error, in which, the concept of concentration of spatial precipitation is firstly proposed. The methods of Inverse Distance Weighting Method, Local Polynomial Method, Radial Basis Function Method, Ordinary Kriging Method and Cokriging Method are used to interpolate rainfall observation data between stations and the mean relative errors between the interpolated and observed results are used to judge the interpolation results. The applicability of spatial interpolation methods under different spatial distribution of precipitation will be finally measured．

precipitation interpolation; concentration of spatial precipitation; method comparison; mean relative error

2015- 11- 08

国家自然科学基金重大项目资助(51190091)

郭卫国(1991—)，男，江西吉安人，硕士研究生，研究方向为水文水资源．

O241.3；P426.62

A

0559- 9342(2016)06- 0014- 04