基于SD模型的细河流域水资源承载能力研究

王 洋

(辽宁省本溪水文局，辽宁本溪117000)



基于SD模型的细河流域水资源承载能力研究

王 洋

(辽宁省本溪水文局，辽宁本溪117000)

立足于水资源可持续发展的基本理念，分析细河流域水资源条件，以水资源—生态—社会经济系统构建指标体系，从而创建基于系统动力学(SD)模型，来实现推求细河流域不同情势下水资源承载能力，进而分析提高该流域水资源承载力的途径。

SD模型；水资源承载能力；细河流域

细河流域地处辽宁省本溪市西部，总面积1 047 km2，为中温带半湿润和半干旱的季风气候区，多年平均降水量为845.0 mm，多年平均地表水资源量为35 919.16万m3，多年平均地下水资源量为7 804.39万m3，多年平均水资源总量为35 974.69万m3。细河流域是本溪市重要的钢铁产业发展基地，随着地区经济的发展，水资源承载力已成为该地区经济社会发展的控制因素。通过开展细河流域水资源承载能力研究工作，分析和给出细河流域不同水平年水资源推荐的配置方案、工程规模和水资源可承载的经济社会发展规模、产业结构与生态环境建设水平等系列成果，可以为今后一定时期内细河流域水资源开发利用和管理提供重要依据，为本溪市总体规划提供参考，促进和保障细河流域人口、资源、环境和经济社会的协调发展。

1 水资源承载能力定义及评价指标构建

1.1 水资源承载能力的定义

当前，水资源承载能力无统一的定义，笔者倾向于：“在未来不同的时间尺度上，以可预见的技术、经济和社会发展水平为依据，以社会可持续发展和水资源可持续利用为原则，以维护生态环境良性发展为条件，在水资源得到合理开发利用和有效配置的前提下，区域内水资源可支撑的水资源—生态—社会经济协调发展的规模”的定义。

1.2 水资源承载能力评价指标构建

区域水资源承载力具有自然、社会双重属性，既反映了水资源系统满足社会经济系统的能力，也与社会经济系统开发自然水资源系统的深度有关。其研究应该兼顾社会、经济、技术和生态等方面。因此，细河流域水资源承载力研究必然涉及细河流域内水资源、社会、经济和生态环境。本研究把水资源、社会、经济、生态环境4个子系统耦合而成的大系统作为细河流域水资源-生态-社会经济系统。

根据水资源承载力的定义、内涵以及水资源承载力指标体系的设计原则和设计方法，在充分分析、比较和借鉴的基础上，本文最后确定了4个子系统10类36个具体指标以构成细河流域水资源承载力指标体系。由于水循环一般以年为周期，所以指标体系中涉及到的时间一般都是以年为单位的，如水资源数量、人均水资源量等都是以一年为周期的。社会经济压力指标有：总人口、城镇人口、工业增加值、建筑业增加值、第三产业增加值、GDP、灌溉面积、牲畜数量等。生态环境压力指标有：绿化面积、环境卫生面积、废污水排放量等。社会经济状态指标有：总需水量、生活需水量、工业需水量、建筑业及第三产业需水量、农业需水量等。生态环境状态指标有：河道外生态需水量、废污水处理率等。社会经济响应指标：人口增长率、城镇化率、工业增加值增长率、产业结构等。生态环境响应指标：废污水排放率、废污水处理投资等。

考虑到水资源承载力指标所具有的区域性，在了解细河流域水资源及开发利用现状的基础上，结合以上水资源承载客体和承载主体的指标，选用7个与水资源和水环境密切相关的综合性变量作为承载力评价指标。这些指标从不同角度反映水资源系统本身的结构组成与人类社会经济活动之间的相互作用关系。详见表1。

表1 水资源承载能力评价指标

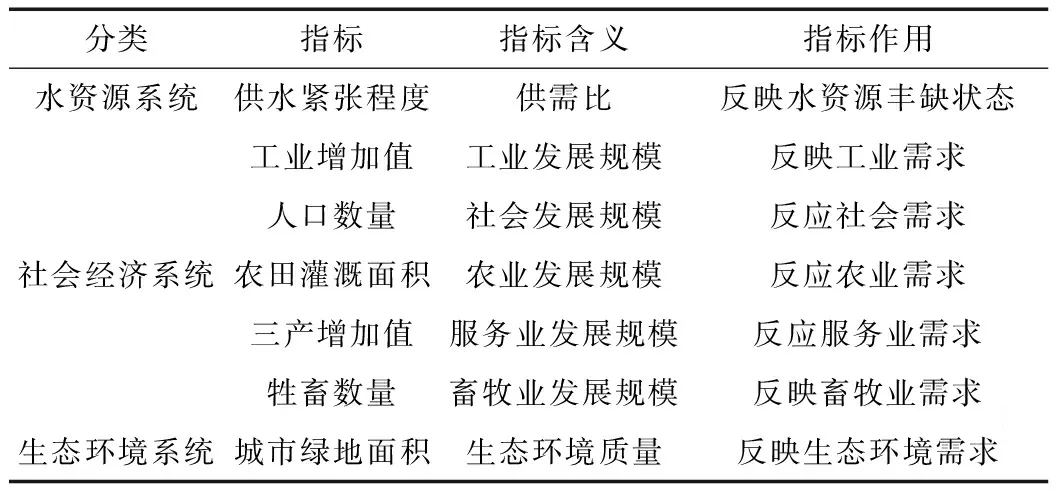
分类指标指标含义指标作用水资源系统供水紧张程度供需比反映水资源丰缺状态社会经济系统工业增加值工业发展规模反映工业需求人口数量社会发展规模反应社会需求农田灌溉面积农业发展规模反应农业需求三产增加值服务业发展规模反应服务业需求牲畜数量畜牧业发展规模反映畜牧业需求生态环境系统城市绿地面积生态环境质量反映生态环境需求

2 系统动力学(SD)简介

系统动力学是美国J.W.Forrester教授于1958年为分析生产管理及库存管理等企业问题而提出的系统仿真方法。其不仅具有系统发展的观点，而且具有分析速度快、模型构造简单、可以使用非线性方程等优点。由于水资源系统是与社会经济系统、 生态环境系统相互作用的复杂系统，因此必须通过建立一套能反映问题本质、技术可行、有科学依据且能反映承载问题多元性、非线性、动态性、多重反馈等特征的模型来研究水资源承载力问题。而系统动力学能把社会经济、资源环境在内的大量复杂因子作为一个整体，通过综合考虑众多因子的相互关系，实现对水资源承载能力的估算和动态变化过程的预测。故，本研究采用系统动力学仿真法(System Dynamics，简称“SD”)建立模型。

3 细河流域水资源承载能力SD模型

3.1 模型基本方程

SD 系统强调对系统整体性和非线性特性的描述。为了清晰地描述系统，一般是在尽量完整地描述系统内各组成部分之间相互作用的非线性关系、复杂的因果反馈关系(Rjk)的基础上，把系统划分成若干个相互关联的子系统(P)，其描述关系式为

S=(P，Rjk)；P={Pi|i∈I} ；

(1)

Rjk={rjk|j∈J，k∈K且J+K=I}

式中，S为整个系统；P为系统S中的子系统，它们可能属于同一层次或不同层次；Rjk为关系矩阵，描述各子系统间的关系，一般是非线性的。

子系统一般由一个或若干个基本单元一阶反馈回路组成，对它们的描述一般用流位变量、流率变量和辅助变量以及其他数学函数、逻辑函数、延迟函数以及常数等。根据SD模型变量与方程的特点，定义变量并给出数学描述

(2)

式中，L为流位变量向量；R为流率变量向量；A为辅助变量向量；为纯速率向量；T为转移矩阵；W为关系矩阵。微分方程

(3)

它是系统动力学的根本基本方程。式中，LET为流位变量；RAT为流率变量。

3.2 SD模型的系统结构与系统

根据本地区特点，将细河流域水资源承载力系统划分为7个子系统：水资源子系统、工业用水子系统、农业用水子系统、生活用水子系统、生态用水子系统、三产用水子系统和废污水子系统(见图1)。其中，水资源子系统和废污水子系统中的中水回用部分是供水系统，工业、农业、生活、生态和三产子系统是需水系统。供水系统与需水系统相互作用，相互限制。

图1 SD模型子系统相互作用示意

从图1可以看出，在系统构建过程中，工业产值决定了工业需水量，三产产值决定了三产需水量，人口数量决定了生活需水量，农田灌溉面积和牲畜数量决定了农业需水量，城市绿地面积、水土流失面积决定了生态需水量；工业、三产、农业、生活、生态五大需水系统和供水系统决定了区域的供需状况，但供需状况反过来又影响工业产值、三产产值、人口、农业灌溉面积、牲畜数量和城市绿地面积等。

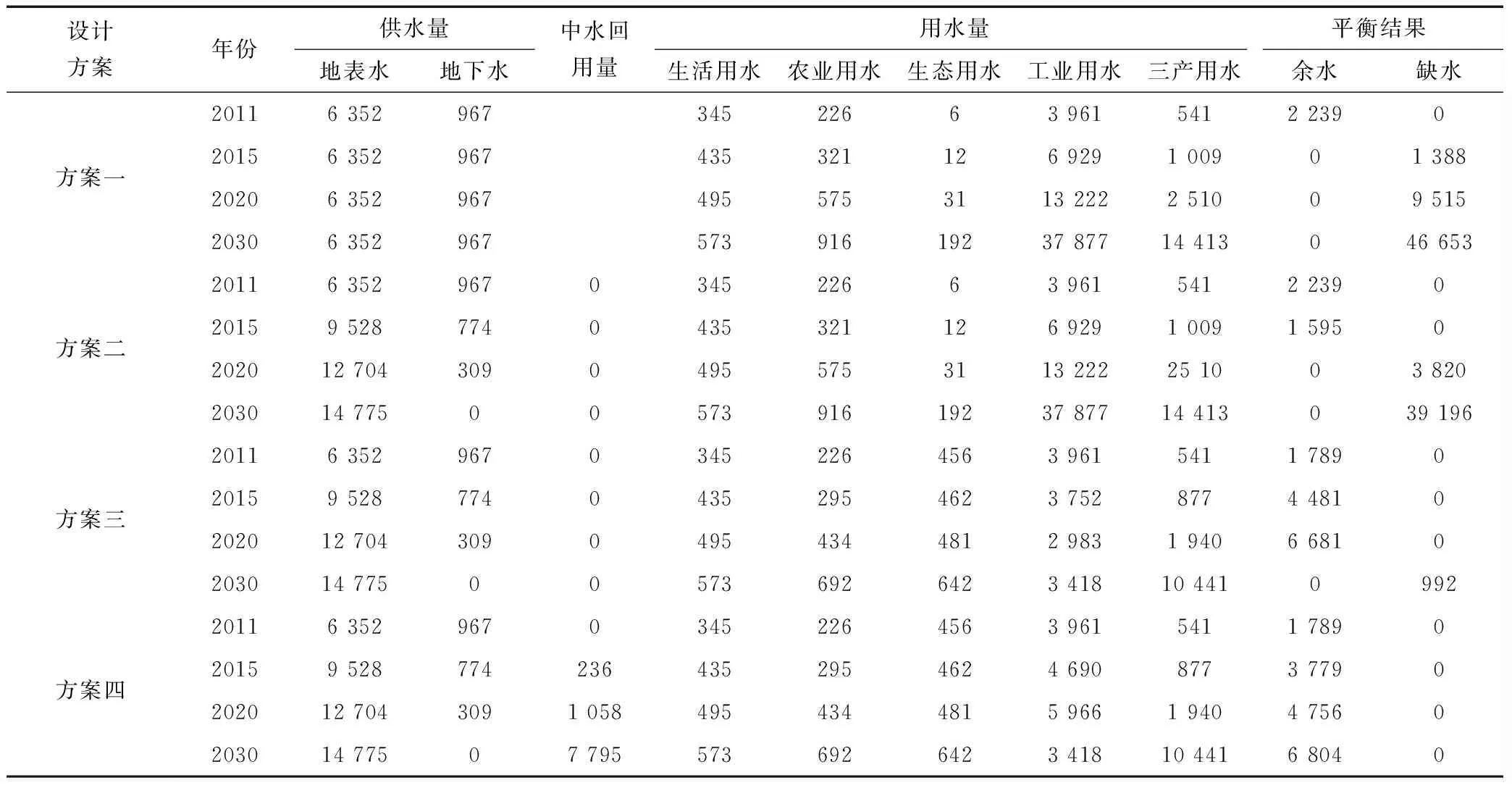
表2 各方案供需平衡分析 万m3

4 方案设计与模拟结果分析

本次研究以根据不同的供需关系(见表2)来确定最优化方案。

方案一：现状延续型，即现状规划方案，工程可供水量按现状取值，未来不发生变化，其余决策指标如工业产值增加率、万元产值用水量等按照以往情形顺延。

方案二：开源型即根据现有工程规划方案，逐年增加地表水源工程，直至与地表水资源可利用量持平，地下水源根据《辽宁省地下水保护规划》，其供水量是逐年减少的，至远期规划年供水量削减至零，其余决策指标按照以往情形顺延。

方案三：开源节流型即供水方案与开源型一致，各行业用水指标与辽宁省实行最严格水资源管理制度“十二五”规划指标逐年接近，其余决策指标按照以往情形顺延。

方案四：节流回用型即供用水方案与开源节流型一致，新增加中水回用量，其余决策指标按照以往情形顺延。

由表2可见，在未来20年里，前3种方案均有不同程度的缺水，仅方案四可以保证经济社会的快速发展。本文将着重分析方案四的模拟结果。

节流回用型方案在前3个方案基础上，考虑废污水回用量来增加供水量，以满足未来需水要求。经过模型模拟，细河流域各个水平年供需平衡，本地水资源可以支撑未来社会经济发展需要。

其各个时期决策变量取值见表3。将各决策变量代入模型，得到的最终模拟结果见表4。

通过层次分析法(AHP)对模拟结果进行归一化处理，可得不同方案下细河流域水资源承载力(见图2)。

方案四综合了开源、节水、治污等措施，使得细河流域水资源承载力的提高大于上述每个方案的提高程度，而且提高的幅度越来越大。该方案全面考虑了开发地表水资源，节约用水和污水治理等主

表3 方案四各个时期决策变量取值

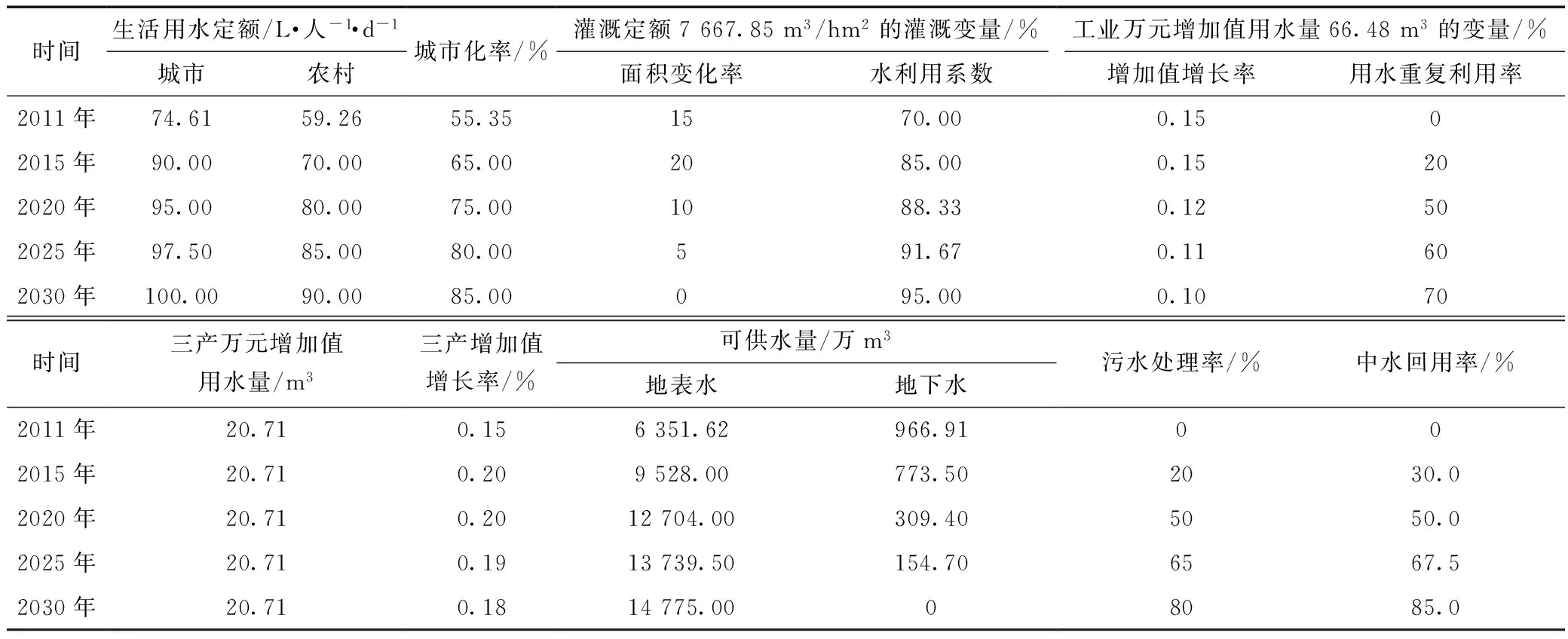
时间生活用水定额/L·人-1·d-1城市农村城市化率/%灌溉定额7667.85m3/hm2的灌溉变量/%工业万元增加值用水量66.48m3的变量/%面积变化率水利用系数增加值增长率用水重复利用率2011年74.6159.2655.351570.000.1502015年90.0070.0065.002085.000.15202020年95.0080.0075.001088.330.12502025年97.5085.0080.00591.670.11602030年100.0090.0085.00095.000.1070时间三产万元增加值用水量/m3三产增加值增长率/%可供水量/万m3地表水地下水污水处理率/%中水回用率/%2011年20.710.156351.62966.91002015年20.710.209528.00773.502030.02020年20.710.2012704.00309.405050.02025年20.710.1913739.50154.706567.52030年20.710.1814775.0008085.0

表4 方案四模拟结果

时间供水紧张程度工业增加值/万元人口数量/人农田灌溉面积/hm2三产增加值/万元城市绿地面积/hm2牲畜数量/头2011年1.441595843139591132.2726117320.00062672.02015年1.8101042130143541246.7248718141.47276178.22020年2.2221988720148636517.441212260103.19697224.92025年1.7393442610153911759.962966520256.784124086.02030年1.4325697140159374880.596960880638.960158369.0

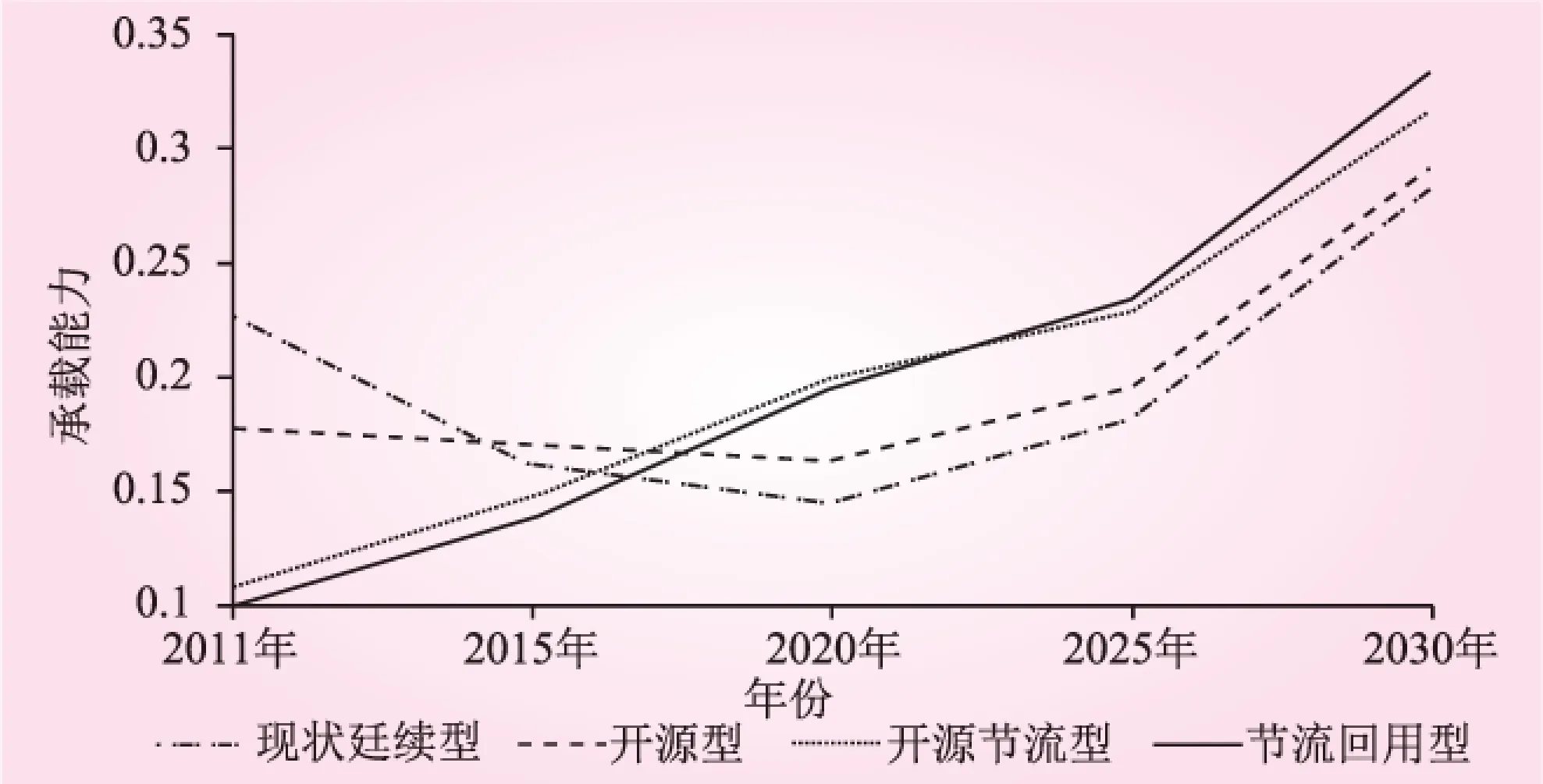
图2 各种方案下水资源承载力结果对比

要措施，既提高水资源的供应量，又加强污水处理回用力度，使细河流域水资源承载力获得了大幅提高，非常有利于细河流域经济、社会与环境协调发展，良好地体现了区域水资源对地区经济、社会、环境和人口的支撑作用，从而使细河流域经济社会发展获得较好的可持续性，所以该方案为最优发展方案。

在节流回用型方案下，细河流域水资源承载力有最大幅度的提高。因此提高污水处理能力，增加中水回用量是提高细河流域水资源承载力的关键所在。目前细河流域仅有一处污水处理工程，中水回用率为零。因此，细河流域迫切需要加大投资力度，修建污水处理及回用工程，提高污水处理率和中水回用率，其具有保护水资源、水环境、增加供水量的多重效益，是解决目前细河流域水污染问题和提高水资源承载力的根本出路。

5 结 语

本研究采用系统动力学法建立SD模型来研究细河流域水资源承载能力。通过模型的试运行和检验，模型模拟仿真程度高，可合理预测未来社会经济发展对水资源的需求。通过模型运行整理四套未来水资源发展方案，模拟结果采用层次分析法(AHP)加以分析，结果显示通过一系列措施，未来细河流域水资源可承载本地区社会经济发展，且认为节水回用型方案是最优选方案。

[1]程莉， 汪德爟. 苏州市水资源承载力研究[J]. 水文， 2010， 30(1)： 47- 50．

[2]孙富行. 水资源承载力分析与应用[D]. 南京： 河海大学， 2005．

[3]董哲仁， 陈明忠. 水资源及水环境承载能力[M]. 北京： 中国水利水电出版社， 2002．

[4]王友贞， 施国庆， 王德胜. 区域水资源承载力评价指标体系的研究[J]. 自然资源学报， 2005， 20 (4)： 597- 604．

[5]朱一中， 夏军， 谈戈. 关于水资源承载能力理论与方法的研究[J]. 地理科学进展， 2002， 21(2)： 180- 188．

[6]魏斌， 张霞. 城市水资源合理利用分析与水资源承载力研究[J]. 城市环境与城市生态， 1995， 8(4)： 19- 24.

(责任编辑 陈 萍)

Study on Carrying Capacity of Water Resources in Xihe River Basin Based on SD Model

WANG Yang

(Benxi Hydrology Bureau of Liaoning Province，Benxi 117000，Liaoning，China)

Based on the idea of sustainable development of water resources，the water resources conditions in Xi River Basin are analyzed.The index system is constructed based on the system of water resources-ecology-society and economy，and then a model based on system dynamics (SD) is created to realize the carrying capacity of water resources of Xi River Basin in different situations.The ways to improve the carrying capacity of water resources in the river basin are also analyzed．

SD model; carrying capacity of water resources; Xi River Basin

2015- 10- 18

王洋(1979—)，男，黑龙江拜泉人，高级工程师，硕士，主要从事水文水资源工作．

TV211.1(231)

A

0559- 9342(2016)06- 0022- 04