基于模糊控制的光伏电池最大功率点跟踪控制系统研究

任 爽, 仲露露

(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)



基于模糊控制的光伏电池最大功率点跟踪控制系统研究

任 爽, 仲露露

(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)

参考国外较新的光伏电池数学模型,运用基于模糊控制的最大功率点跟踪(MPPT)控制算法,搭建BOOST仿真电路,并在MATLAB中进行系统仿真,实现了光伏电池最大功率点的跟踪控制与最大功率输出.模糊逻辑控制算法的控制效果,证实了模糊控制较其他MPPT控制方法具有更加优异控制性能,且控制效果让人十分满意.

光伏电池; 模糊逻辑控制;MPPT;MATLAB

高效应用太阳能是人们一直追求的目标,光伏发电自1839年法国物理学家A.E.贝克勒发现“光生伏特效应”后,随着异质结新型高分子光伏材料[1]的应用及新型光伏控制系统的发展,其效率有了突破,可达35%,光伏产业的发展迎来新的格局.在整个光伏发电系统中,光伏电池技术和光伏变换技术是最重要的两大关键支撑技术.最大功率点跟踪(MPPT)技术是其变换技术中关键的技术之一,提高MPPT技术是光伏逆变器应用过程中的重点和难点.

1 光伏电池最大功率点控制系统

1.1BOOST升压调节电路的设计

光伏电池最大功率点的提取是通过利用阻抗匹配来实现的,我们可以利用BOOST升压电路来实现,通过调节占空比来达到改变电路内阻的目的.占空比的产生,通过由功率变化为输入变量,占空比为输出变量的MPPT控制算法来得到[2].所以,组成此系统的三大主要部分分别为:光伏电池,MPPT算法控制,BOOST升压电路,如图1所示. 依据BOOST电路的组成,需要对电路中的电感,电容,电阻等元件参数进行计算以确定适合本系统.

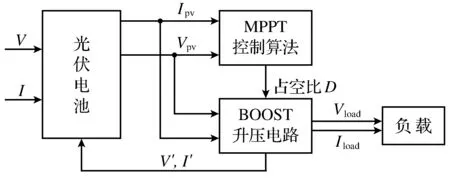
图1 光伏电池MPPT控制系统框图

对电路的分析可知,使流经电感的电流处于连续状态其临界条件是式(1)中的等式.开关频率f选取为20kHz.

(1)

式中,IL为电感电流;D为占空比;T为光照时间;L为电感系数;Ud为标准条件下光伏电池的最大功率点电压;Imax为临界值最大电流.因为储能电感在电路中处于电路的输入端,也就是指电源的输入电流式.将式(1)变换后得到输入电流临界连续时的最小电感为:

(2)

式中,Lmin为最小电感;由标准条件下电池的参数得:

(3)

1.2MPPT模糊控制器设计

1.2.1 模糊控制器的模糊子集与结构的确定

光伏电池的功率曲线为只有一个峰值的单峰值曲线,有一个对应的最大功率点的电压,此时有dPpv/dUpv=0.所以,可以把dPpv/dUpv作为模糊控制器的偏差输入E(n),把dPpv/dUpv的变化率作为模糊控制器的偏差变化率CE(n)输入.输出为BOOST调节电路占空比D(n),通过实时检测输出功率与电压的数据来追踪控制最大功率点.输入表达式如下:

(4)

输出为BOOST调节电路占空比D(n).当前采样值和上次采样值分别用n与n-1来表示,根据这个特性,模糊控制器被设计为双输入单输出的二维结构.使用默认的mamdani推理方法,解模糊使用重心法,输入为E(n)和CE(n),模糊化后,经过模糊规则与隶属度函数推理再经过解模糊化得输出D(n)[3].模糊子集与论域的设定:E(n)与CE(n)设定为{NLNANSZEPSPAPL},含有7个模糊变量描述其大小的模糊子集的D(n)也设定为{NLNANSZEPSPAPL},也含有7个模糊变量描述占空比整定步长的模糊子集.表示的含义分别为负大,负中,负小,零,正小,正中,正大. 论域范围为:E(n)为{-1 1},CE(n)为{-10 10},D(n)为{0.1 0.7}.

1.2.2 模糊规则的确定

(l) 当E(n)<0且CE(n)<0时,工作点位于Pmax的右边,且正在远离Pmax;

(2) 当E(n)<0且CE(n)>0时,工作点位于Pmax的右边,且正在向Pmax靠近;

(3) 当E(n)>0且CE(n)<0时,工作点位于Pmax的左边,且正在向Pmax靠近;

(4) 当E(n)>0且CE(n)>0时,工作点位于Pmax的左边,且正在远离Pmax.

模糊控制规则的设定主要根据以上四条结论,使E(n)始终向零的方向靠近,使光伏电池工作一直以最大功率点输出.依据上述原理,在距离最大功率点拐点较远时,采用较大的调节步长,反之则采用较小的调节步长,进行对BOOST升压电路的MOSFET管的占空比调节,完成对光伏电池系统的MPPT控制[4].得到的控制规则如表1所示.

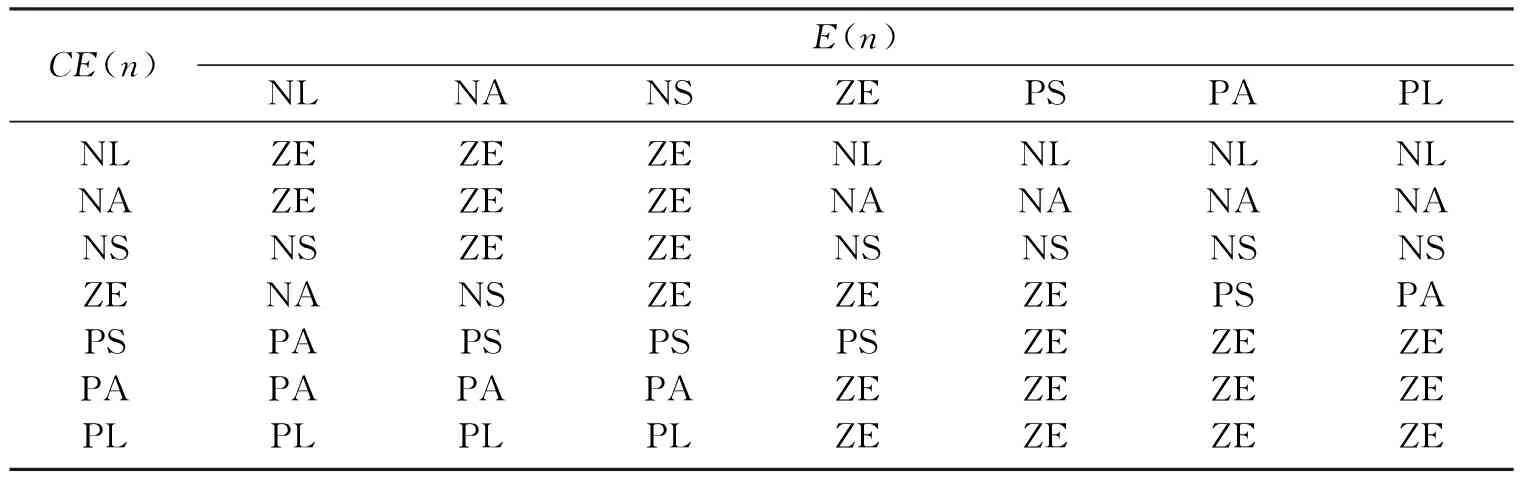
表1 模糊控制规则表

2 光伏电池MPPT系统建模与仿真

光伏电池输出的功率与电压经过模糊控制器的运作推理最后得出占空比信号,用于控制BOOST电路,BOOST电路经过升压调节,把输出的最大功率点电压再输出给光伏电池,从电池中提取出最大的功率,使电池一直工作在最大功率点.光伏电池模型仿真图如图2所示,其中封装为子系统的光伏电池模型如图3所示.

在MATLAB中搭建模糊控制的光伏电池最大功率点跟踪控制系统仿真图,如图4所示.采用固定步长为0.000 01 s,仿真时间为0.005 s,仿真算法为ode8(Dormand prince),经过反复调试,E(n)量化因子为25～28,

CE(n)量化因子为100

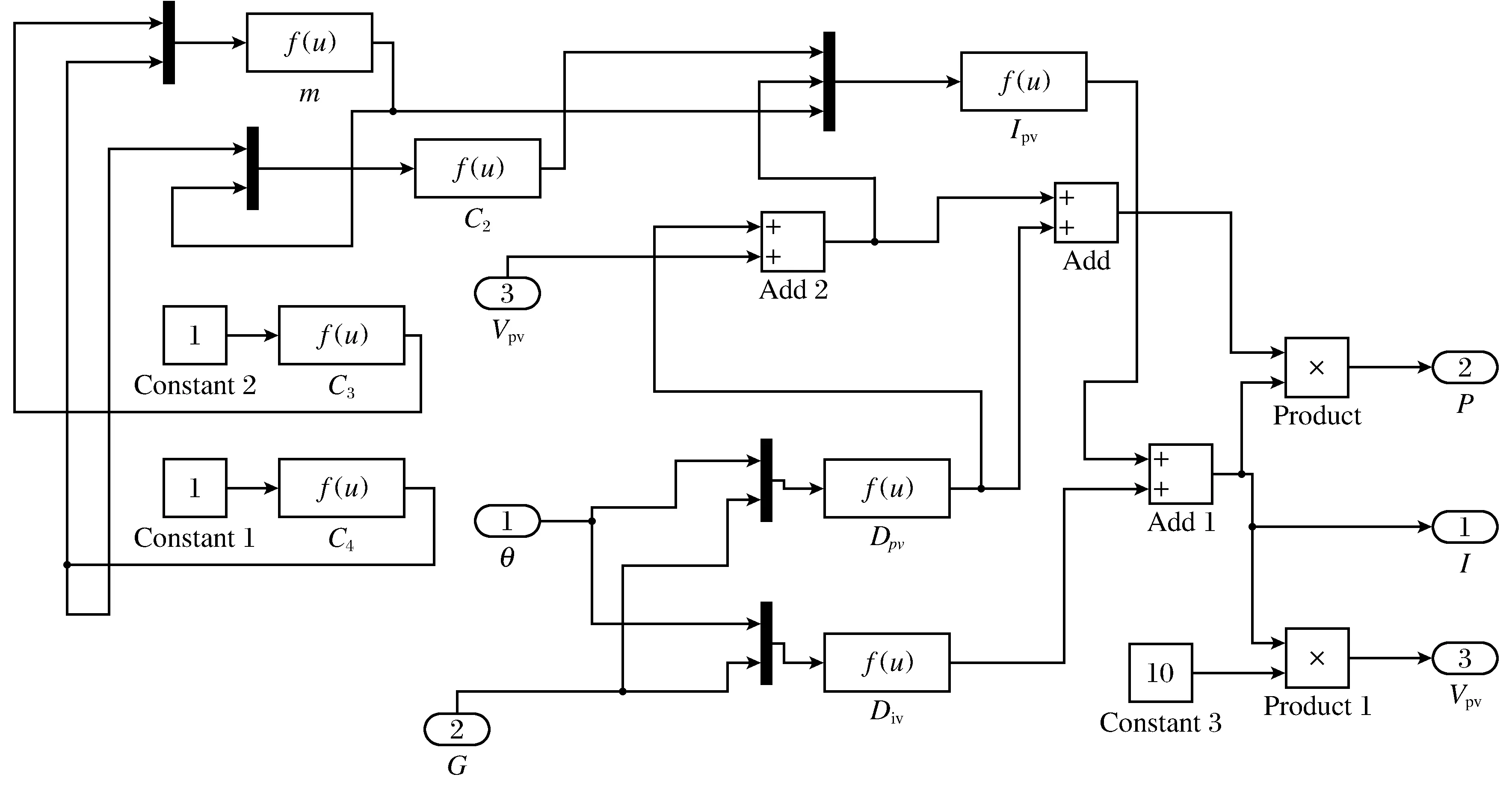
图2 光伏电池模型仿真图

图3 封装为子系统的光伏电池模型

图4 系统仿真图

～110,输出D(n)为占空比.仿真的结果如下,分别从电池输出的功率、电流、电压及控制器波形来分析系统的控制性能[6].分别通过改变光照强度与温度来验证系统的跟踪控制性能[6].使用SIMULNK里的阶跃信号来模拟光照与温度的突变,更能检验系统的响应与调整性能.如图5～图8为θ=25 ℃并保持不变,在0.003s时,给一个光照G从400W/m2跃迁到600W/m2时的阶跃信号,运行后得到光伏电池功率、电压、电流输出波形及模糊控制器的输出波形.

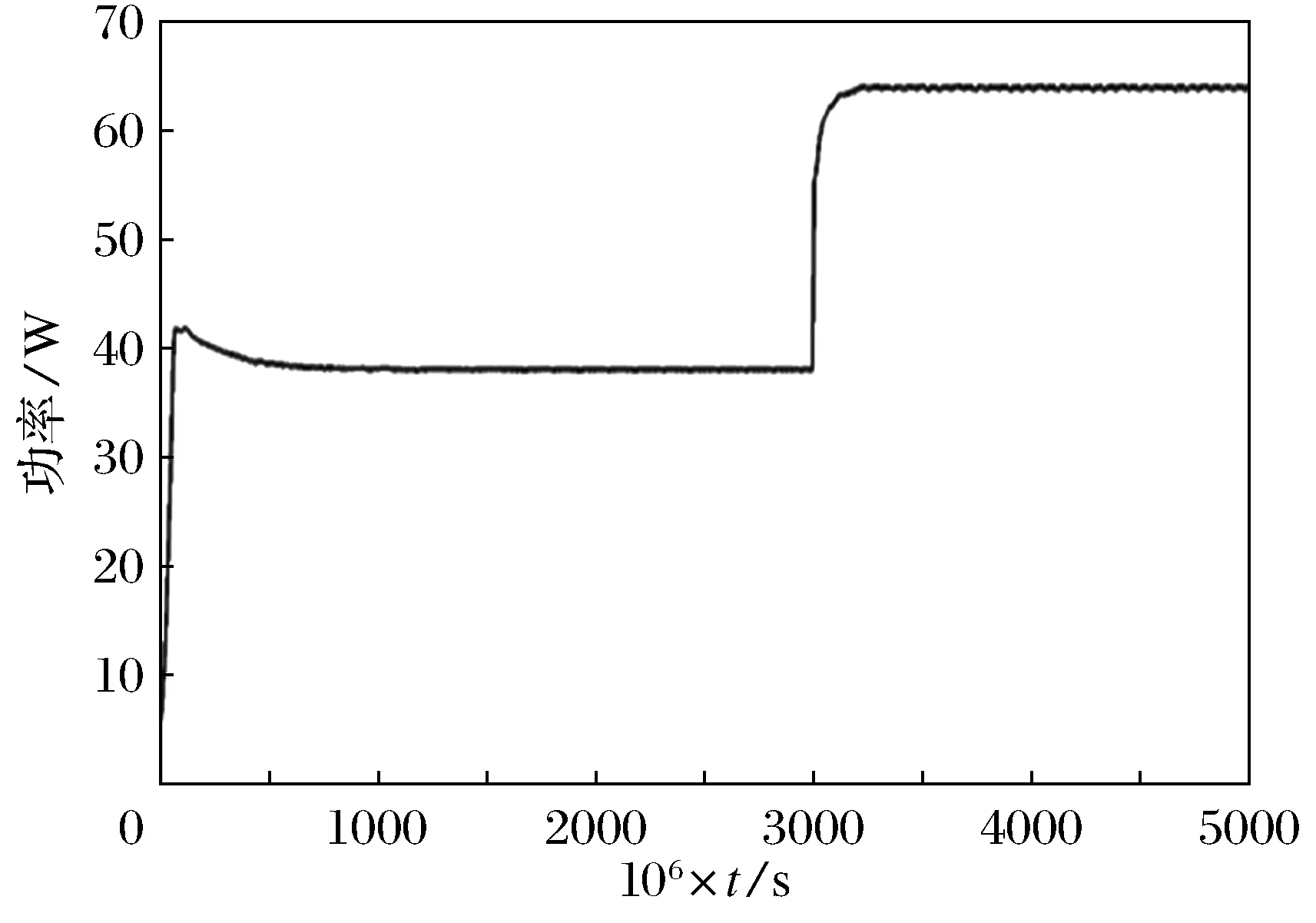
图5 光照G从400 W/m2跃迁到600 W/m2

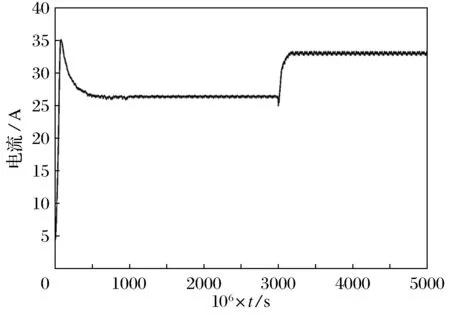
图6 光照G从400 W/m2跃迁到600 W/m2

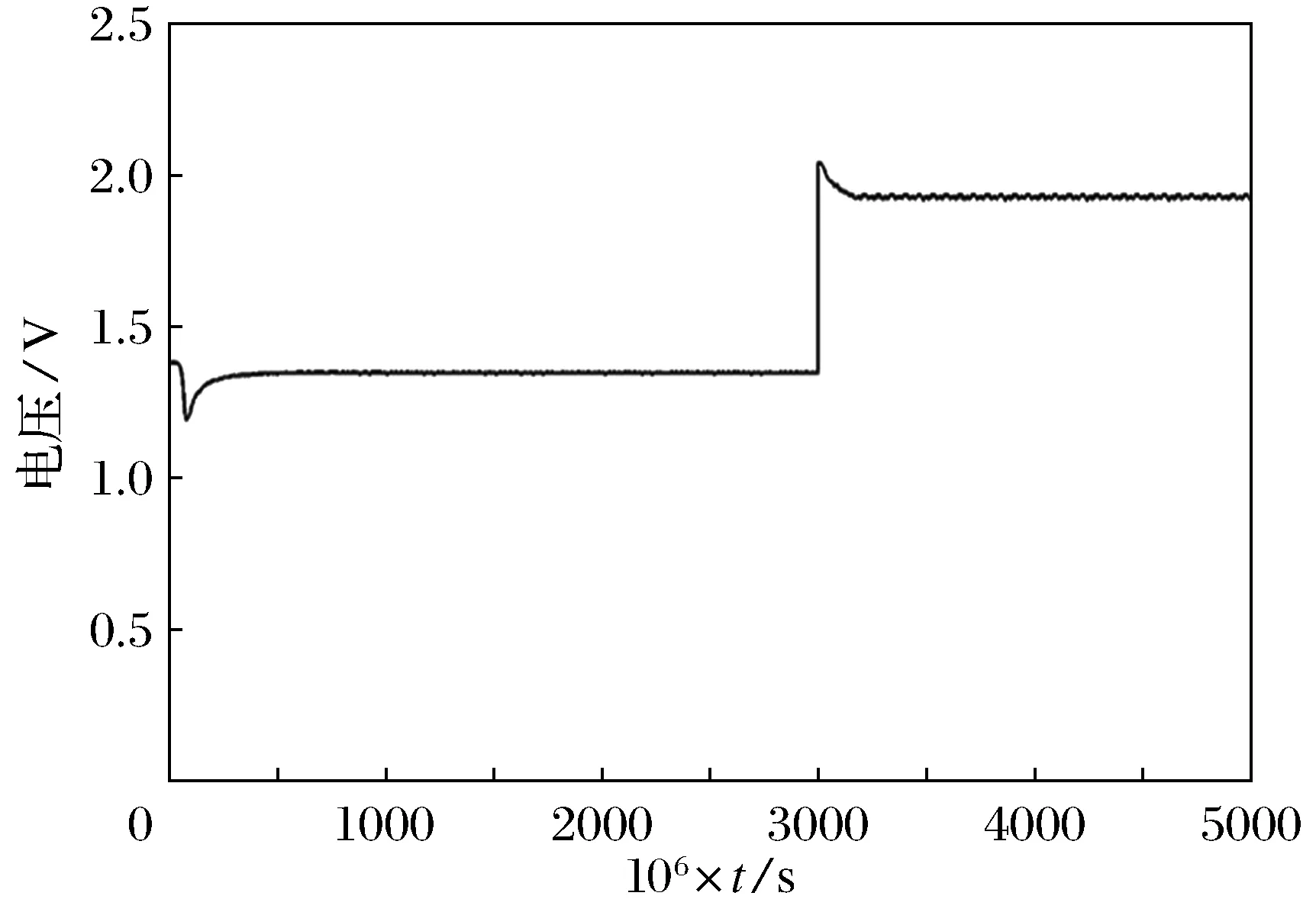
图7 光照G从400 W/m2跃迁到600 W/m2

图8 光照G从400 W/m2跃迁到600 W/m2

从功率图形可以看出,光伏电池一直以最大功率点输出,且在0.003s光照发生突变后在0.000 05s准确跟踪到最大功率点并保持其输出.且输出平稳波动量小,误差为1W以内,精度较高并一直准确在最大功率点处运行.电压与电流输出也十分平稳,响应时间快,控制器的输出波形亦如此.如图9～图12为G=1 000W/m2并保持不变,在0.003s时,给一个温度θ从25 ℃跃迁到50 ℃时的阶跃信号,运行后得到光伏电池功率、电压、电流输出波形及模糊控制器的输出波形.

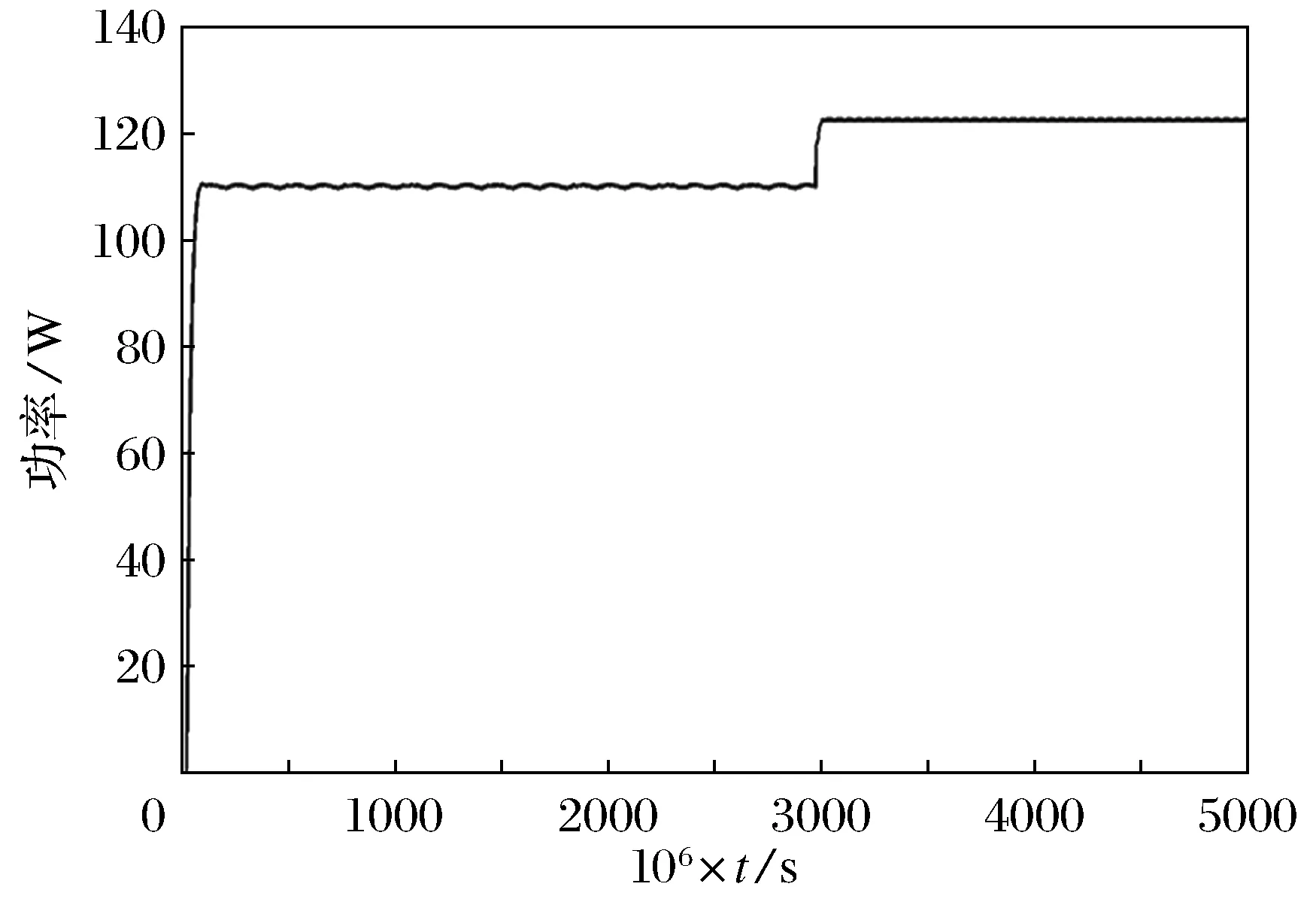
图9 温度θ从25 ℃跃迁到50 ℃时

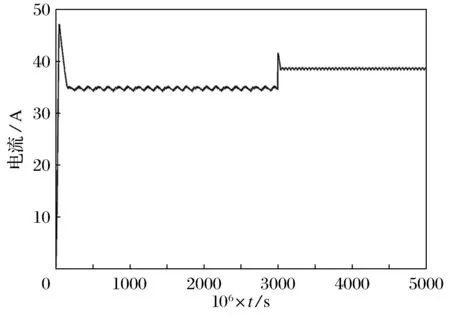
图10 温度θ从25 ℃跃迁到50 ℃时

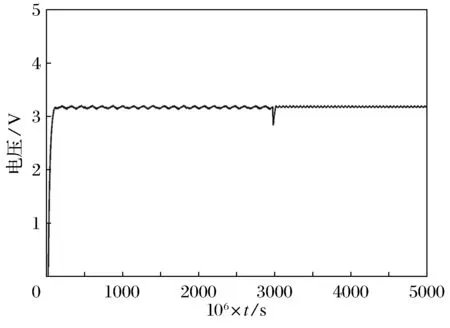
图11 温度θ从25 ℃跃迁到50 ℃时

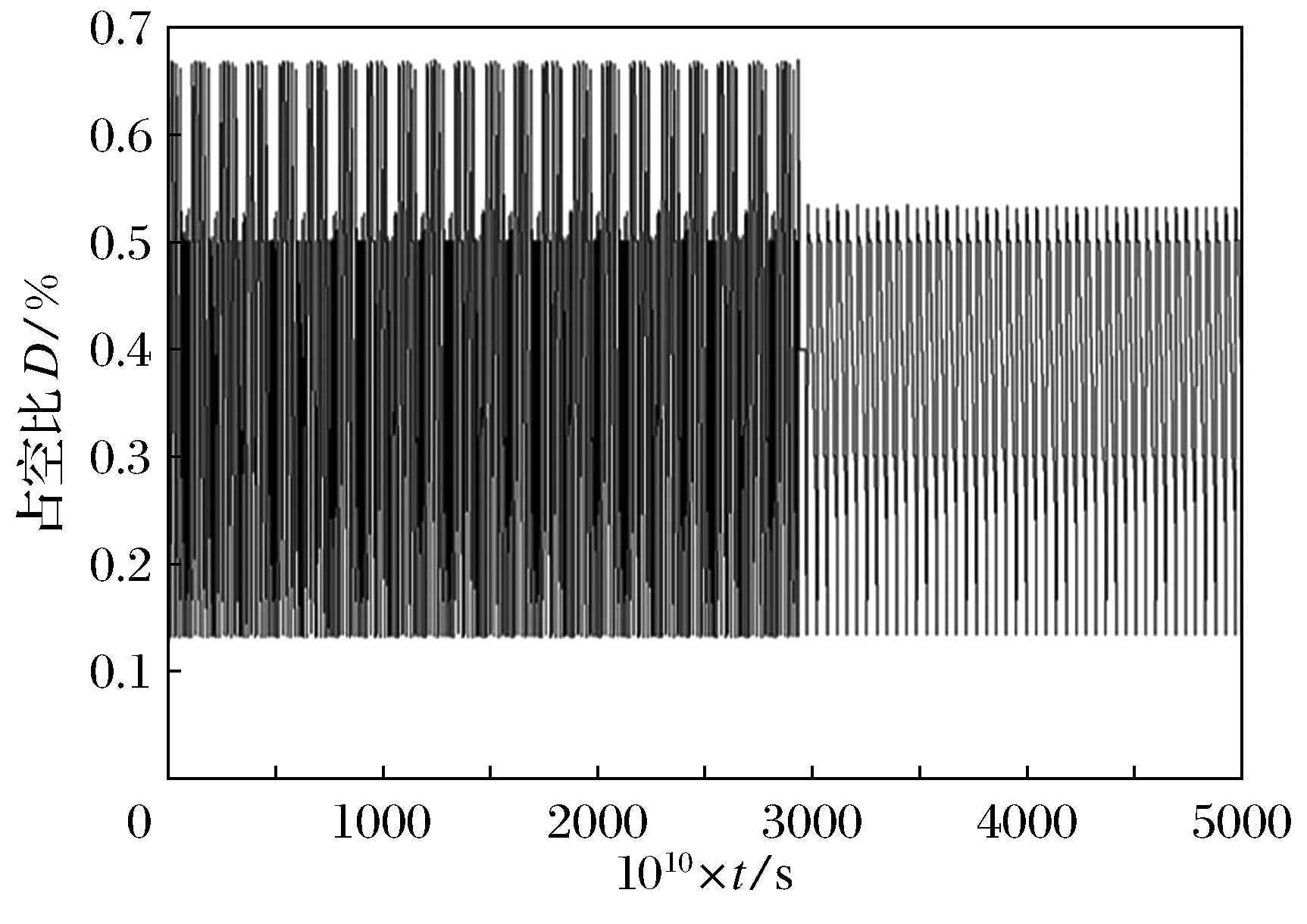
图12 温度θ从25 ℃跃迁到50 ℃时

对比光照影响的控制器输出波形可以看出,温度θ对功率的影响程度不及光照G影响大.在模糊控制器调节下,光伏电池一直以最大功率点输出,且在0.003s光照发生突变后在0.000 05s后能准确跟踪到最大功率点并保持其输出.且输出平稳波动量小,误差为1W以内,精度较高,并一直准确在最大功率点处运行.电压与电流输出也十分平稳,响应时间快,控制器的输出波形也如此.

参考期刊与其他论文资料,对比分析了几种MPPT控制方法的仿真性能(见表2).

由表2可知,开路电压比例法的稳定性是优异的,但是在环境剧烈变化的时候,无法准确的跟着MPPT,鲁棒性(控制系统在一定(结构,大小)的参数摄动下,维持其他某些性能的特性)差,导致了较大的功率损失,降低了MPPT控制器的性能.扰动观察法的稳定性与响应时间是良好的,但其最大的缺点是容易引起误判,导致失调与振荡,从而也会使输出功率损失较大.电导增量法的计算方法是好的,不过由于一般实际应用中会把DI/DU为零的状态定义为一个阈值区间,这样也会引起跟踪误差,但总体运行效果还是较好的[7].本文基于模糊控制方法MPPT控制的模糊控制器的控制性能的各项指标都十分优异,得益于模糊控制器的精益设计.在模糊控制器的设计中,模糊规则的定义,输入的定义范围,量化因子的选择都显得尤为重要.

表2 常用MPPT方法控制性能对比

3 总 结

本文根据光伏电池机理进行了仿真建模,并在此基础上进行模糊控制仿真研究.由于光照与温度对光伏电池有一定影响,本文设计的基于模糊控制的光伏MPPT系统可以使光照和温度对光伏电池的干扰降到最小,根据仿真结果可知,无论在响应时间,稳定性,鲁棒性上本设计的控制器都有极佳控制性能,应用前景十分良好.

[1] 赵争鸣,陈剑,孙晓瑛. 太阳能光伏发电最大功率点跟踪技术[M]. 北京:电子工业出版社, 2010:1-70.

(ZHAOZM,CHENJ,SUNXY.Photovoltaicmaximumpowerpointtrackingtechnology[M].Beijing:ElectronicIndustryPress, 2010:1-70.)

[2]LISW.AMPPTcontrolstrategywithvariableweatherparameterandnoDC/DCconverterforphotovoltaicsystems[J].SolarEnergy, 2014,108:117-125.

[3]MAJM,MANKL,TINGTO,etal.Approximatesingle-diodephotovoltaicmodelforefficientI-Vcharacteristicsestimation[J].ScientificWorldJournal, 2013(1):230471.

[4]ALIM,MARCELLOC,MIRKODG,etal.Adutycycleoptimizationbasedhybridmaximumpowerpointtrackingtechniqueforphotovoltaicsystems[J].InternationalJournalofElectricalPowerandEnergySystems, 2014,59(7):141-154.[5] 吴琼,原忠虎,王晓宁. 基于偏最小二乘回归分析综述[J]. 沈阳大学学报, 2007,19(2):33-35.

(WU Q, YUAN Z H, WANG X N. Review of partial least squares regression analysis[J]. Journal of Shenyang University, 2007,19(2):33-35.)

[6] 王丽萍,张建成. 光伏电池最大功率点跟踪控制方法的对比研究及改进[J]. 电网与清洁能源, 2011,27(2):52-55.

(WANG L P, ZHANG J C. Comparative study and improvement of the maximum power point tracking control method for photovoltaic cells[J]. Power Grid and Clean Energy, 2011,27(2):52-55.)

[7] 刘英英. 非均匀采样数据系统的量化控制[J]. 沈阳大学学报(自然科学版), 2015(5):400-404.

(LIU Y Y. Quantization control of non uniformly sampled data systems[J]. Journal of Shenyang University(Natural Science), 2015,27(5):400-404.)

【责任编辑: 赵 炬】

Photovoltaic Cells MPPT Control System Based on Fuzzy Control

RenShuang,ZhongLulu

(College of InformationEngineering, Shenyang University of Chemical Technology, Shenyang 110142, China)

By referencing the newer mathematic model of photovoltaic cell in foreign books, using MPPT based on fuzzy control designs BOOST circuit and simulates in MATLAB, the maximum power point tracking control and maximum power output of photovoltaic cells are realized. The control effect of the fuzzy logic control algorithm verifies that, the method of fuzzy control has more outstanding performance than other common control methods and it is satisfying.

photovoltaic cell; fuzzy logic control; MPPT; MATLAB

2016-05-29

国家自然科学基金资助项目(61034006); 辽宁省博士启动资金资助项目(201501072).

任 爽(1987-),女,辽宁沈阳人,沈阳化工大学工程师,硕士.

2095-5456(2016)05-0410-06

TP

A