基于一类二阶线性变参系统特征结构配置的完全参数化方法

安博林

(东北电力大学自动化工程学院，吉林 吉林 132012)

基于一类二阶线性变参系统特征结构配置的完全参数化方法

安博林

(东北电力大学自动化工程学院，吉林 吉林 132012)

二阶线性时变参数系统 特征结构配置 比例微分控制律 航天器在轨加油

非线性系统在混沌运动控制[1]、最优控制[2]、模糊建模[3]、鲁棒控制[4]及预测控制[5]等工程领域有着十分广泛的应用前景。众所周知，非线性系统的线性变参增益调度控制可以看作是线性控制技术向非线性控制技术的一种拓展[6,7]。在实际应用中许多非线性系统可以由线性变参系统代替。由于一个多变量线性变参系统的稳定和动态表现与该系统的特征结构配置息息相关，因此对于系统特征结构配置问题的研究在控制理论及其应用方面具有十分重要的意义。

考虑一类通过比例微分控制来解决其特征结构配置问题的二阶线性变参系统：

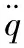
(1)

其中，q(t)是状态向量,q(t)∈Rn；u(t)是输入向量，u(t)∈Rr；θ(t)为时变参数向量，θ(t)=[θ1(t),θ2(t),…,θN(t)]T∈RN；A(θ)、B(θ)和C(θ)均为θ(t)的显函数，A(θ)∈Rn×n，B(θ)∈Rn×r，C(θ)∈Rn×n，B(θ)为关于θ(t)的满秩矩阵。

假设1 [A(θ)B(θ)]关于θ(t)为能控。

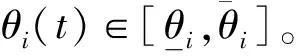
通过矩阵变换可以将二阶线性变参系统(1)等效成一个一阶线性变参系统：

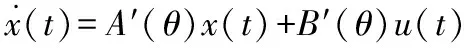
(2)

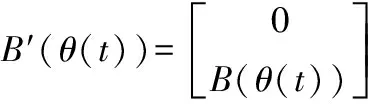
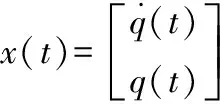
(3)

但是这不可避免地涉及到2n维矩阵的操作从而导致计算较为繁琐，因此如何减少计算量，提出一个更为简洁有效的方法成为了研究学者迫切需要解决的问题。

在矩阵对[A(θ)B(θ)]能控的前提下，笔者提供了一个通过比例微分反馈来解决二阶线性变参系统特征结构配置问题的简洁完整的参数化方法以及基于闭环特征值和一组参数向量的针对闭环特征向量和反馈增益的简洁完整的参数化表达式。上述闭环特征值和参数是根据该闭环系统的各种需要所选取的。笔者提出的方法之所以简洁是因为该方法的计算量主要集中在两个多项式矩阵的化简或者两组在事先选取合适闭环特征值前提下的奇异值分解，而且只是直接利用原有系统的系数A(θ)、B(θ)和C(θ)，所涉及到的操作仅仅针对n维矩阵。

1 问题描述

比例微分控制律为：

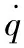
K(θ)=[K0(θ)K1(θ)]

(4)

将式(4)应用到系统(1)或(2)中，即可获得如下形式的闭环系统：

(5)

其中，

Ac(θ(t))=A′(θ(t))+B′(θ(t)K(θ(t))

(6)

基于一般情形考虑，进行如下推导。

令Γ(θ)={si(θ),si(θ)∈C,i=1,2,…,n′，1≤n′≤2n}为矩阵Ac(θ)的一组特征值，并且该组特征值关于实轴对称(共轭复数)。设上述特征值si(θ)的代数重数和几何重数分别为mi和qi,则在矩阵Ac(θ)的Jordan标准型F(θ)中有qi个与特征值si(θ)相关的Jordan块。若记这些Jordan块的阶数为pij，j=1,2,…,qi，则有：

(7)

(8)

其中满足式(7)的Γ(θ)和pij，qi，mi，i=1,2,…,n′，j=1,2,…，qi,可以描述成如下形式：

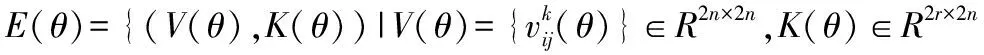
将式(8)转换成如下参数化形式：

A′(θ)V(θ)+B′(θ)K(θ)V(θ)=V(θ)F(θ)

(9)

其中F(θ)∈R2n×2n为Ac(θ)的Jordan形式。

综上所述，通过比例微分控制律(4)来解决二阶线性变参系统(1)的特征结构配置问题(ESA)描述如下：

给出矩阵A(θ)、C(θ)∈Rn×n、B(θ)∈Rn×r和一系列共轭复数si,i=1,2,…,2n，找到所有满足式(9)的矩阵K(θ)∈Rr×2n和V(θ)∈C2n×2n，其中det(V(θ))≠0且矩阵A′(θ)和B′(θ)均由式(3)构成。

笔者的主要目的就是在矩阵对[A(θ)B(θ)]能控的情况下，为解决二阶线性变参系统(1)的特征结构配置问题提供一个操作过程直接针对原系统系数A(θ)、B(θ)和C(θ)的简洁方法。

2 初步分析

众所周知，当且仅当下式成立的前提下矩阵对[A(θ)B(θ)]才可以保证能控：

rank[A(θ)-sIB(θ)]=n,∀s∈C

(10)

当式(10)成立时，则存在一对幺模矩阵P(θ，s)和Q(θ,s)满足：

P(θ,s)[A(θ)-sIB(θ)]Q(θ,s)=[0I]

(11)

对Q(θ,s)进行如下分块：

(12)

将K(θ)=W(θ)V-1(θ)代入到式(9)中得到如下Sylvester方程：

A′(θ)V(θ)+B′(θ)W(θ)=V(θ)F(θ)

(13)

因此二阶线性变参系统的特征结构配置问题就转化成了Sylvester方程(13)的求解问题，其中矩阵V(θ)∈Cn×p和W(θ)∈Cr×p即为所求。

引理1 令[A(θ)B(θ)]为能控，则式(13)所有的解决方案可以归纳为如下形式：

(14)

或者等效为：

vi(θ)=Q12(θ,si(θ))P(θ,si(θ))ri+Q11(θ,

si(θ))fi(θ)

wi(θ)=Q22(θ,si(θ))P(θ,si(θ))ri+Q12(θ,

si(θ))fi(θ)

(15)

i=1,2,…,p

其中fi(θ)∈Cr,i=1,2,…,p为一组任意参数向量。

构建一组能控的矩阵对[A′(θ)B′(θ)]，则下述结论成立。

引理2 若[A(θ)B(θ)]为能控，则所构建的矩阵对[A′(θ)B′(θ)]也是能控的，当且仅当如下条件满足时：

rank[Q12(θ,s)P(θ,s)C(θ)+sInQ11(θ,s)]=n,

∀s∈C

(16)

同时式(16)也可以等效为存在一组幺模矩阵H(θ,s)和L(θ,s)，满足：

H(θ,s)[Q12(θ,s)P(θ,s)C(θ)+sIn-Q11(θ,s)]·

L(θ,s)=[0In]

(17)

并将式(17)中的多项式矩阵L(θ,s)分块成如下形式：

(18)

然后引出下面的定理。

引理3 假设式(17)对于幺模矩阵H(θ,s)和L(θ,s)均成立，则存在所有向量y(θ)和z(θ)满足：

[Q12(θ,s)P(θ,s)C(θ)+sIn]y(θ)-Q11(θ,s)z(θ)=0

(19)

其中y(θ)、z(θ)满足如下条件：

y(θ)=L11(θ,s)g(θ),z(θ)=L21(θ,s)g(θ)

(20)

且g(θ)∈Cr为任意参数向量。

3 ESA问题的解决方案

设

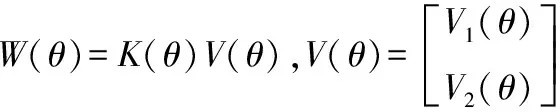
(21)

则式(9)可以被分解为如下形式：

V2(θ)=V1(θ)F(θ)

(22)

A(θ)V2(θ)+B(θ)W(θ)=V2(θ)F(θ)-C(θ)V1(θ)

(23)

由此可得式(23)符合式(13)形式，根据引理1得：

V2i(θ)=-Q12(θ,si(θ))P(θ,si(θ))C(θ)v1i(θ)+

Q11(θ,si(θ))fi(θ),i=1,2,…,2n

(24)

wi(θ)=-Q22(θ,si(θ))P(θ,si(θ))C(θ)v1i(θ)+

Q21(θ,si(θ))fi(θ),i=1,2,…,2n

(25)

式(22)可以等效写成如下形式：

v2i(θ)=si(θ)v1i(θ),i=1,2,…,2n

(26)

式(24)和式(26)联立可得：

[Q12(θ,si(θ))P(θ,si(θ))C(θ)+si(θ)In]v1i(θ)-Q11(θ,si(θ))fi(θ)=0,i=1,2,…,2n

(27)

由于式(27)符合式(19)的形式，则根据引理3可得：

v1i(θ)=L11(θ,si(θ))gi(θ),i=1,2,…,2n

(28)

fi(θ)=L21(θ,si(θ))gi(θ),i=1,2,…,2n

(29)

其中gi(θ)∈Cr,i=1,2,…,2n为一组任意参数向量。

将式(28)代入式(26)中可得：

v2i(θ)=si(θ)L11(θ,si(θ))gi(θ),i=1,2,…,2n

(30)

此外，将式(28)、(29)代入式(25)中，可以得到向量wi(θ),i=1,2,…,2n和参数向量gi(θ),i=1,2,…,2n的表达式。因此，可以获得如下定理来求解该系统的ESA问题。

定理1 若[A(θ)B(θ)]和[A(θ)′B′(θ)]均为能控，则综合上述推理可以得到该系统特征结构配置问题的求解方案：

(31)

K(θ)=W(θ)V-1(θ)

(32)

其中矩阵W(θ)由wi(θ)构成：

wi(θ)=[Q21(θ,si(θ))L21(θ,si(θ))-Q22(θ,si(θ))·P(θ,si(θ))C(θ)L11(θ,si(θ))]gi(θ),i=1,2,…,2n

(33)

且gi(θ)∈Cr(i=1,2,…,2n)是一组满足下述约束条件的参数向量：

约束条件C2 det[V]≠0

上述定理中的约束条件C1是为了保证式(21)或式(32)中的矩阵K(θ)为实。

4 数值算例

参考一个在文献[8]中提供的航天器在轨加油的一般过程，该航天器在轨加油的姿态动力学模型可以表示成如下形式：

(34)

其中φ(t)、φ(t)、ψ(t)表示航天器的俯仰角、滚动角、偏航角；ω0表示轨道角速度；Ix(t)、Iy(t)、Iz(t)表示航天器的转动惯量I(t)在坐标系下的各轴分量；Ux、Uy、Uz表示航天器在坐标系各轴上的力矩分量。

先通过矩阵变换求得模型(34)满足式(1)的参数矩阵：

(35)

q=[φ(t)φ(t)ψ(t)]T为状态向量，u=[UxUyUz]T为输入向量，而θ=[Ix(t)Iy(t)Iz(t)]T为时变参数向量。矩阵对[A(θ)B(θ)]和[A′(θ)B′(θ)](由式(3)定义)在该系统中均为能控。

通过计算易得一组满足式(11)的幺模矩阵P(θ,s)和Q(θ,s)：

P(θ,s)=diag[1 1 1]

(36)

(37)

同时还可以获得一组满足式(17)的幺模矩阵H(θ,s)和L(θ,s)：

H(θ,s)=diag[1 1 1]

(38)

(39)

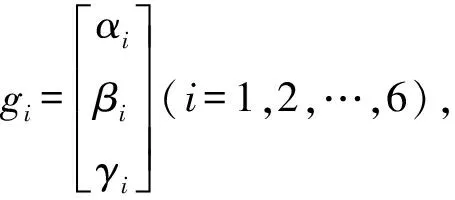
V=[αiβiγisiαisiβisiγi]T,i=1,2,…,6

(40)

进一步由式(33)可以求得矩阵W(θ,s)：

(41)

众所周知，如果一个矩阵的Jordan型是一个对角矩阵，那么该矩阵的特征值对于矩阵中的参数扰动并不敏感。因此，出于鲁棒性和减少对参数扰动敏感性的考虑，选取不同的闭环系统特征值如下：

(42)

其中由式(35)给出的aij和bij均为关于时变参数向量θ[Ix(t)Iy(t)Iz(t)]T的函数。

将所设计的状态反馈控制器(42)应用到航天器在轨加油姿态控制系统模型(34)当中去。假设该航天器的姿态角速度均为0°/s(即0rad/s)，初始姿态角均为1°(即0.0175rad),在初始状态下，x(0)=[0 0.0175 0 0.0175 0 0.0175]T闭环系统3个姿态角的初始值响应和仿真结果如图1所示。从图中可以看出，3个姿态角的时间响应变化迅速且稳态误差最终趋于0。

图1 姿态角的时间响应

仿真结果表明：所获得的比例微分控制律保证了所设计的闭环系统的稳定性，同时也验证了前文推导出的算法的有效性和实用性。

5 结束语

解决了一类基于比例微分控制律的二阶线性变参系统的特征结构配置问题，并提出了两个分别针对闭环特征向量矩阵和反馈增益的简洁完整的参数化表达式。上述主要的操作过程在于两组初等矩阵的变换或者两组奇异值分解，计算量仅仅涉及到n维矩阵。然后选取合适的自由参量和闭环特征值来获得满足系统要求的比例微分控制律。最终通过一个航天器在轨加油姿态控制系统模型来验证所推导出的线性变参控制方法的实用性和有效性，同时从仿真结果中可以得出上述线性变参控制律保证了所设计闭环系统的稳定性并提供了良好的性能。

[1] 韩明君，李有堂，朱丽，等.干气密封系统轴向非线性动力稳定性[J].化工机械，2012，39(3)：308～312.

[2] 高德欣，杨晓燕.受扰动非线性系统的反馈线性化最优控制[J].化工自动化及仪表，2010，37(8)：19～22.

[3] 赵艳东，任宪勇，张兴隆，等.基于阶跃模型的非线性模糊PID控制算法研究[J].化工自动化及仪表，2010，37(7)：28～31.

[4] 周硕.一类非线性不确定时滞系统鲁棒预测控制[J].化工自动化及仪表，2011，38(2)：149～152.

[5] 张燕，申森.基于快速正交搜索算法的非线性预测控制[J].化工自动化及仪表，2014，41(11)：1226～1244.

[6] Rugh W J,Shamma J S.Research on Gain Scheduling[J].Automatica,2000,36(10)：1401～1425.

[7] Leith D J,Leithead W E.Survey of Gain-scheduling Analysis and Design[J].International Journal of Control,2000,73(11)：1001～1025.

[8] 张龙.航天器在轨加注的姿态动力学与控制[D].哈尔滨:哈尔滨工业大学，2009.

(Continued on Page 538)

CompletelyParameterizedApproachforEigenstructureAssignmentinSecond-orderLinearParameter-varyingSystem

AN Bo-lin

(SchoolofAutomationEngineering,NortheastDianliUniversity,Jilin132012，China)

TP13

A

1000-3932(2016)05-0457-06

2016-04-06(修改稿)