浓度调节器的仿真与研究

吴雯婷 潘 聪 闫晓芳 于 良 程保国

(1．南京邮电大学光电工程学院，南京 210023；2.航天城工程指挥部，北京 100094)

浓度调节器的仿真与研究

吴雯婷1潘 聪2闫晓芳2于 良2程保国2

(1．南京邮电大学光电工程学院，南京 210023；2.航天城工程指挥部，北京 100094)

首先对线性和压差式两种典型的浓度调节器模型进行了分析和仿真验证。然后，基于微流控等效电路理论提出了一种电路式模型浓度调节器的设计方案，并通过COMSOL软件对所提出的物理模型进行验证。仿真结果表明：在层流条件下，等效电路理论对微流体系统的分析完全正确，可以成功获得线性和非线性流体的各种浓度分布情况。

浓度调节器 微流控 等效电路理论

在过去的几十年里，为了实现集成式芯片实验室系统，生物和化学的分析、实验设备开始向着小型化、微型化发展[1]。而微流控技术是芯片实验室技术的支撑技术之一，在生物化学领域引起广泛关注[2]。最近的一些研究表明，微流控技术可以提供稳定的梯度式浓度分布环境，为生物细胞研究工作提供一个良好的平台[3]。其中，线性浓度分布有助于试剂的配置和检测；非线性浓度分布则有助于癌细胞抗药性的研究[4]。为了产生浓度的各种分布形式，现有的很多微流控装置大多是采用复杂的结构设计或添加多种浓度的试剂[5]。文献[6，7]两个科研小组已经提出了线性和压差式两种典型的浓度调节器模型，在简化结构的同时又能达到浓度的分布要求，笔者对这两种模型进行了仿真研究。

随着研究的深入，微流控等效电路理论成功地把流体分析与电路分析进行了类比[8]，提高了微流控设计的效率，降低了分析的难度。当流体满足下列条件时：不可压缩、粘度各项同性、无对流；稳态的层流；沿着流道的方向压力均匀梯度分布，广义的哈根-泊肃叶公式可以直接用来分析矩形或其他形流道的流体属性。另外，如果系统的工作频率较低，小于流体的共振频率并且器件制作材料足够硬，那么流感(类比于电感)和流容(类比于电容)可以忽略[9]。因此，整个系统的分析就等效为纯流阻(类比于电阻)网络分析。笔者基于等效电路理论，提出了一种浓度调节器设计方案，并结合仿真软件对其物理模型进行模拟，理论分析和仿真结果一致。笔者所用模具制作均采用聚二甲基硅氧烷(PDMS)材料。

1 理论背景①

微通道网络可以精确控制两种溶液(缓冲液和样品)的体积混合比，因此它们可以产生一组定义好的体积浓度。如果缓冲液的初始浓度不是零，充分混合后的混合物浓度值C为：

(1)

广义的哈根-泊肃叶公式为[10]：

(2)

根据式(2)可知，当两段流体的压力降相等时，液体的流量与流阻成反比；若整个系统的流道横截面相同，流阻就正比于流道长度，进而流量比与流道长度比成反比，即：

(3)

其中，LB和LS分别是两种溶液充分混合前所流过的流道长度。

2 线性模型仿真研究

2.1原理分析与建模

由式(3)可知，在对称流道中，液体的浓度比与长度比成反比。因此，可以在结构完全对称、输入条件完全相同(仅浓度不同)的情况下设计一种线性浓度调节器，如图1所示。

a. 结构示意图

b. 三维图图1 线性浓度调节器模型

这个模型是二输入九输出的，为了提高仿真效率，实际仿真时去掉了输入部分的蜂窝结构，直接模拟混合直管道，如图2所示。该模型由3层结构组成：上层——输入层，左右旋转对称；下层——输出层；中间——上下联通管道。以浓度口(出口)1为例：当左右两个不同浓度的液体入口压力降Δp相等时，浓度口1的浓度C1出=C高L1低+C低L1高/(L1高+L1低)，其他浓度口计算方法相同。

a. 仿真浓度分布图

b. 9个浓度口的归一化浓度值图2 线性模型仿真结果

2.2仿真验证与分析

在建立模型时，整个系统的横截面尺寸一致：流道高度h=60μm、宽w=100μm。为保证层流条件，每个入口的压力设置为10Pa，出口压力为0Pa；左端入口液体浓度为0mol/m3，右端入口液体浓度为100mol/m3。利用浓度口的面平均浓度探针分别测量各个浓度口的浓度，从数据拟合结果可以看出，浓度结果近似直线分布，与预期的设计要求一致。仿真结果与理论值的略微偏差可能是由软件的精度造成的。经过反复实验可知：随着网格的细化，软件计算量增大，误差将减小(同理适用于下面的仿真分析)。

线性模型的设计理论简单，所得线性溶液浓度效果理想，但是对模型的物理空间消耗较大。因此，对浓度梯度设计要求较细腻时，此方法不一定最优。

3 压差式模型仿真研究

3.1原理分析与建模

该模型建立浓度梯度的基本原理是依靠液压差将样品溶液注入一系列并联的微通道中，然后在主流道中混合，浓度的分布由微通道的长度分布决定。从压差式模型结构原理(图3)的结构可以看出，主流道的横截面尺寸远大于微通道的尺寸，因此主流道的流阻相较于微流道流阻可以忽略；上下两个主流道结构完全相同且初始条件一致，唯一的区别是错排放置，这就使得每一段微通道具有上下压差Δp′，借此压力差，不同浓度的流体可以在下层主通道中得到混合。流量Q与微通道长度L的关系为[11]：

(4)

式中r——微通道的横截面半径。

由式(4)可知，流量Q与微通道的长度L成反比。各个检测口的归一化浓度与相应微通道长度的关系为[7]：

(5)

图3 压差式模型结构原理

3.2仿真验证与分析

仿真中主通道的横截面尺寸为20μm×100μm(宽×高)，微通道横截面尺寸为10μm×4μm，为使上下两个主通道的入口压力足够小以满足层流条件，设为10Pa，废弃液排泄口压力为0Pa。在仿真中共设有7个检测口，采用域平均浓度探针测浓度值。整个模型的压差Δp=10Pa，上下主流道错排压力差Δp′=Δp/3。仿真结果如图4所示，各个检测点的浓度与拟合直线基本吻合，呈线性分布。当其他的实验条件不变，仅将微通道的长度重新排列时浓度就会改变。图5所示为微通道长度按二次多项式排列的仿真结果，从图5b可以看出检测口浓度按照多项式曲线分布，仿真结果与理论分析一致，压差式模型仿真成功。

a. 仿真浓度分布

b. 7个浓度口的浓度值图4 压差式模型按线性设计仿真结果

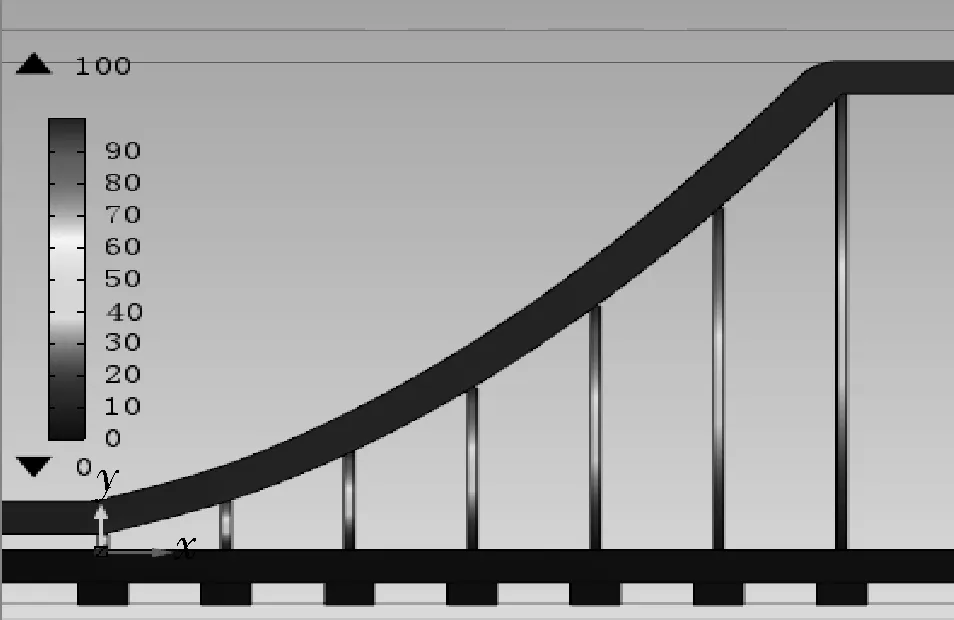
a. 仿真浓度分布

b. 7个浓度口的浓度值图5 压差式模型微通道按多项 式设计仿真结果

压差式模型所占空间和设计耗时较少，而且可以选择性地设计线性和非线性的浓度梯度分布。但是该设计也存在一定的缺陷：所得不同浓度的液体只有在浓度口可用，排泄口浓度是单一的。因此，采用这种设计方案时，只有在浓度口外加连通器引出混合后的液体或是将“实验场所”直接设置在浓度口下方的腔中。

4 电路式模型设计与研究

4.1模型的设计原理

首先，假定需要设计的微流控网络由NS段流道、NM个回路、NN个节点、NF个输入和NO个输出组成。其中回路是最简形式，然后按照下面的步骤进行分析：

a. 利用等效电路理论将系统转化成纯流阻网络；

b. 将每一部分的流量Q和流阻RH标注清楚，并将流向用箭头标示，这样就得到了NS个流量值和NS个流阻值；

c. 在每一个节点处，按照基尔霍夫电流定律(KCL)列出NN个质量守恒等式；

d. 列出整个系统的质量守恒等式，即总输入流量等于总输出流量；

e. 在每一个回路中，按照基尔霍夫电压定律(KVL)列出NM个能量守恒等式。

将所有的等式组成方程组并求解，最后用电路仿真软件或流体模拟软件进行仿真验证。

4.2物理模型的建立

按照4.1节的方法设计一个二输入五输出的浓度调节系统，如图6所示，输出端浓度分别以0%、25%、50%、75%、100%这样的线性分布。该模型的横截面尺寸一致：高h=60μm、宽w=100μm；浓度口1～5的流量都为60nL/min；整个系统由15段流道、6个回路、7个节点、2个输入、5个输出组成。在设计流道时，每段长度L必须大于液体的完全扩散混合长度LD[12]。在该系统中，以水为例算出的LD水≈1.67mm，为了在大流量的情况下也满足完全混合条件，笔者设定系统的最小混合流道长度Lmin=10mm，则L2=L8=L11=Lmin=10mm。为了简化模型，令L7=L10=L12=L14=L15=2mm，L13=6mm。

a. 结构示意图

b. 等效电路图图6 等效电路式浓度调节系统

利用等效KCL公式列出节点方程组：

节点1Q12=Q13+Q9+Q6+Q1

节点2Q2=Q6+Q7

节点3Q8=Q7+Q3

节点4Q8=Q9+Q10

节点5Q11=Q10+Q4

节点6Q11=Q13+Q14

节点7Q15=Q14+Q5

(6)

按照浓度要求可得：Q6︰Q7=1︰1，Q10︰Q9=2︰1，Q14︰Q13=3︰1，解方程组得Q6=Q7=Q9=Q13=30nL/min，Q8=Q14=90nL/min，Q10=60nL/min，Q11=120nL/min，Q12=Q15=150nL/min，至此确定了两个输入端Q12和Q15的流量相等。

结合式(2)、(3)和等效KVL公式，列出回路方程组：

回路1Q1L1=Q6L6+Q2L2

回路2Q3L3=Q7L7+Q2L2

回路3Q4L4=Q10L10+Q8L8+Q3L3

回路4Q5L5=Q14L14+Q11L11+Q4L4

回路5Q6L6=Q9L9+Q8L8+Q7L7

回路6Q9L9=Q13L13+Q11L11+Q10L10

(7)

解方程得：L1=L5=51mm，L3=11mm，L4=28mm，L6=82mm，L9=50mm。

4.3仿真验证与分析

按照4.2节所得数据，采用COMSOL仿真软件进行模拟实验，结果如图7所示。

a. 仿真浓度分布

b. 5个浓度口的归一化浓度值图7 等效电路式模型仿真结果

在每一个浓度口处采用一个面平均浓度探针测量系统稳态时的浓度，归一化浓度为测量值与初始样品浓度的比值。由图7b所示的归一化浓度结果可知，理论值与仿真结果一致，相对误差在0.0%～1.1%范围内，表明该设计方案仿真成功。按照这种设计方案，不仅可以实现线性浓度分布，还可以按照不同的需求，调整模型的尺寸结构，实现指数、对称以及其他的非线性浓度分布形式。

5 结束语

笔者仿真研究了线性和压差式两种设计浓度调节器的方案，提出一种电路式浓度调节器模型，并通过仿真手段进行了验证，结果表明基于等效电路理论的微流控分析是正确可行的。等效电路理论的应用不要求设计人员具有很高的流体知识和软件操作能力，只要求对系统的一些具体要求和基本的流体理论有一定的了解。笔者所展示的是一种设定浓度口比和流量，反向推导入口浓度和系统尺寸的过程，应用等效电路理论，完全可以进行一种已知入口条件和浓度口条件，推导系统设计尺寸的设计。所有的设计方案都只需要两个输入，简便易行，但是所有的设计只在流体条件满足层流的情况下适用，一旦系统处于高压或大流量的情况，现有的分析就会出现偏差，这是仍需改进的地方。

[1] 周云龙,刘博,孙科.T形微通道内氮气/非牛顿流体两相流相分配[J].化工机械,2013,40(4)：429～435.

[2] 李辉,林立,邱雄迩.电渗流速度检测系统设计[J].化工自动化及仪表，2015,42(3):245～248.

[3] Jeon N L, Baskaran H, Dertinger S K W,et al. Neutrophil Chemotaxis in Linear and Complex Gradients of Interleukin-8 Formed in a Microfabricated Device[J].Nature Biotechnology,2002,20(8):826～830.

[4] Wang S J, Saadi W, Lin F,et al.Differential Effects of EGF Gradient Profiles on MDA-MB-231 Breast Cancer Cell Chemotaxis[J].Experimental Cell Research, 2004,300(1):180～189.

[5] Dertinger S K W, Chiu D T, Jeon N L,et al.Generation of Gradients Having Complex Shapes Using Microfluidic Networks[J]. Analytical Chemistry, 2001,73(6):1240～1246.

[6] Yamada M, Hirano T, Yasuda M,et al. A Microfluidic Flow Distributor Generating Stepwise Concentrations for High-throughput Biochemical Processing[J]. Lab Chip, 2006, 6(2):179～184.

[7] Li C W,Chen R S，Yang M.Generation of Linear and Non-linear Concentration Gradients along Microfluidic Channel by Microtunnel Controlled Stepwise Addition of Sample Solution[J].Lab Chip,2007,7(10):1371～1373.

[8] Meng E. Biomedical Microsystems[M].Boca Raton：CRC Press,2010.

[9] Kim D, Chesler N C，Beebe D J.A Method for Dynamic System Characterization Using Hydraulic Series Resistance[J].Lab Chip, 2006,6(5):639～644.

[10] Lee K, Kim C, Ahn B,et al. Generalized Serial Dilution Module for Monotonic and Arbitrary Microfluidic Gradient Generators[J].Lab Chip, 2009,9(5):709～717.

[11] White F.Viscous Fluid Flow[M].Boston：McGraw-Hill,1991.

[12] Oh K W,Lee K,Ahn B,et al.Design of Pressure-driven Microfluidic Networks Using Electric Circuit Analogy[J].Lab Chip,2012,12(3):515～545.

(Continued from Page 1064)

AbstractA new three-dimensional fractional-order chaotic system was introduced.Through theoretical analysis, solving Lyapunov exponent and dimension and changing the order of new fractional-order chaotic system, the variation in the system’s state trajectories and attractor verifies the system effectiveness; meanwhile, through analyzing the concept of tracking signals and simulating the working principle of integer-order chaotic synchronization controller, a new nonlinear controller was developed.Both theoretical derivation and Matlab simulation shows that, this nonlinear controller can bring about better projective effect between the fractional-order chaotic system and the integer-order chaotic system.

Keywordsfractional-order chaotic system, integer-order chaotic system, projective synchronization, nonlinear controller, Matlab

SimulationandResearchofConcentrationRegulator

WU Wen-ting1, PAN Cong2,YAN Xiao-fang2,YU Liang2，CHENG Bao-guo2

(1.SchoolofOptoelectronicEngineering,NanjingUniversityofPostsandTelecommunications,Nanjing210023,China; 2.ConstructionHeadquartersofAerospaceCity,Beijing100094,China)

The commonly-used linear and differential pressure concentration regulators were analyzed and simulated; and basing on the theory of microfluidics equivalent circuit, a design scheme for circuit model-based concentration regulator was proposed and its physical model was verified with COMSOL software.The simulation results indicate that, under laminar flow conditions, having the equivalent circuit theory based to analyze microfluidics system is correct and both linear and non-linear distribution of various concentrations can be obtained successfully.

concentration regulator, microfluidics, equivalent circuit theory

TH861

A

1000-3932(2016)10-1048-06

2016-09-06(修改稿)

江苏省光电通信工程技术研究中心项目(ZSF0402)；江苏省普通高校研究生科研创新计划项目(CXZZ13_0465)