基于CEEMD和谱峭度的轴承故障诊断

姜建国 刘盈萱

(东北石油大学电气信息工程学院，黑龙江 大庆 163318)

基于CEEMD和谱峭度的轴承故障诊断

姜建国 刘盈萱

(东北石油大学电气信息工程学院，黑龙江 大庆 163318)

针对共振解调在滚动轴承故障诊断应用中带通滤波器参数选择困难的情况，提出一种互补总体平均经验模态分解方法(CEEMD)与谱峭度相结合的轴承故障诊断新方法。通过实际信号验证了该方法的可行性与准确性。

轴承 故障诊断 互补总体平均经验模态分解 谱峭度

故障诊断是根据系统的测量数据和故障库中的知识来判断系统是否发生故障的过程[1]。共振解调是滚动轴承故障诊断中最常用的方法之一，其原理是根据实际需要选择某一高频固有频率作为研究对象，通过中心频率等于该固有频率的带通滤波器进行带通滤波，从而将固有振动信号分离出来[2～4]，再通过包络检波器进行检波，去除信号中的高频成分，从而得到只含有故障特征信息的低频包络信号。通过对该低频包络信号进行频谱分析就可诊断出故障信息。然而共振解调法涉及参数的设定，这需要依靠操作者的能力和经验，限制了共振解调的应用范围。

Dwyer首先提出了谱峭度，将谱峭度视为一个统计量作为传统功率谱密度的补充，用来检测含噪信号中的瞬态成分。Vabrie针对平稳信号作了进一步的研究，对谐波过程的特性刻画提出一些方法。为了更准确地定义非平稳过程的谱峭度，Antoni J通过Wold-Cramer分解来定义谱峭度[5]，该定义使得对谱峭度及其一些特性有了新的理解，开辟了谱峭度在机械故障诊断应用中的新前景。

经验模态分解(EMD)是由Huang N E和Wu Z H最先提出的[6]，该方法将信号分解为有限个具有瞬时物理意义的内敛模态函数(IMF)，但由于EMD分解法中相似尺度信号可能存在于不同的IMF分量中，因此限制了其发展。后来Deering R和Kaiser J F通过向待分解信号中添加掩膜信号的方法来均匀原始信号极值点的分布[7]，达到了抑制模态混淆的目的。随后Wu Z H和Huang N E提出了噪声辅助方法分析，通过向原始信号中加入一定的白噪声，使得不同尺度上的信号具有连续性[8]，该方法称为集合经验模态分解(EEMD)。为避免加入的白噪声随机性太强，无法彻底中和。Yeh对EEMD做了更深层次的改进，通过加入大小相等、符号相反的辅助噪声来消除信号中残余的辅助噪声，该方法称为互补集合经验模态分解(CEEMD)。

1 CEEMD分解①

1.1 CEEMD原理

CEEMD通过对分解信号中添加符号相反的高斯白噪声，既保证了信号的连续性，得到最佳的IMF分量，又防止了添加的白噪声不能被完全中和的问题。其算法步骤如下[9]：

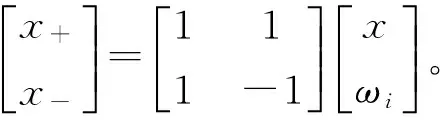
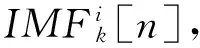
CEEMD分解的过程需要确定两个参数[11]：白噪声的幅值k和CEEMD的分解次数n。Wu Z H和Huang N E建议k以原信号x(t)的标准偏差与一个分数的乘积来赋值，这样当n为数百次的时候，残留噪声引起误差就低于1%。

1.2IMF分量的选择

CEEMD虽然能够有效地解决模态混叠问题，但由于插值误差或过度分解等原因仍存在伪分量，伪分量所含有的频率与特征频带可能会出现重合，因此会干扰诊断结果。峭度是反映波形尖峰度的数值统计量，它描述了振动信号的分布特征，峭度值K的定义如下：

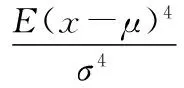
(1)

轴承正常运行时，振动信号近似服从正态分布，因此IMF分量的峭度值约为3。当轴承发生故障时，由于故障引起的冲击影响，包含故障信息的IMF分量的峭度值将大于3，因此可以利用峭度值作为故障内敛模态函数的选择条件从而剔除分解过程产生的伪分量[12]。

2 谱峭度

谱峭度最初定义建立在短时傅里叶变换基础上，直到Antoni J提出正式定义才有其独立分支。目前，国内对谱峭度法的研究大多都是建立在Antoni J定义的基础上，通过不同的信号处理方法实现窄带定位并滤波。谱峭度法为合理选择滚动轴承振动信号包络解调的中心频率和带宽提供了便利。在非平稳情况下，信号X(t)的Wold-Cramer分解频域表达式为：

(2)

其中，Y(t)为信号X(t)激励的系统响应；H(t，f)是随机量，为系统时变传递函数，即信号Y(t)在频率f处的复包络[13]，可表示为H(t,f,w)，w为滤波器时变性的随机变量。

基于四阶谱累积的谱峭度定义为：

(3)

其中，S2nY(t,f)为2n阶瞬时矩阵，是复包络能量的度量：

(4)

因此，谱峭度定义成归一化累积量，则概率密度函数H的峰值度量为[14]：

(5)

在机械故障诊断中，振动信号往往包含故障信号和强烈的噪声信号：

Z(t)=X(t)+N(t)

(6)

其中，Z(t)为测得的振动信号，X(t)为被检测的故障信号，N(t)为加性噪声。

滚动轴承故障会引起一系列反复瞬时冲击力[14]，激起系统的部分结构共振，X(t)的通用模型为：

X(t)=∑kXkh(t-τk)

(7)

其中，h(t)是单个冲击引起的脉冲响应，Xk是各个脉冲的随机幅值，τk是脉冲的发生时间。

此时谱峭度可表示为[13]：

(8)

其中，ρ(f)为信噪比，ρ(f)=Sn(f)/Sf(f)，Sn(f)和Sf(f)分别为n(t)和f(t)的功率谱密度[11]。由式(8)可知，在信噪比很高的频率处，KZ(f)≈KX(f)；在信噪比很低的频率处，KZ(f)≈0。所以应用谱峭度于不同频带时，可以细查整个频域来寻找故障信号，从而寻求最优故障频带。

3 CEEMD和谱峭度结合的轴承故障检测

3.1实验流程

将CEEMD分解后的本征模态函数进行峭度计算，不仅可以将故障信号提取出，还能够有效地剔除伪分量，从而达到减少低频干扰、突出高频共振成分，并有效地提高信号信噪比的目的。谱峭度法可以根据峭度最大化原则自动确定带通滤波器的相关参数，合理地解决了带通滤波器参数选择的难点。为此，笔者提出一种基于CEEMD和谱峭度结合的滚动轴承早期故障诊断新方法，诊断流程如图1所示。

具体流程描述如下：

a. 对采集的滚动轴承振动信号进行CEEMD分解,得到一系列具有不同特征尺度的IMF分量；

图1 笔者所提方法滚动轴承故障诊断流程

b. 计算CEEMD分解后的每个IMF分量的峭度值；

c. 筛选出峭度值大于3的IMF分量，并将峭度值大于3的IMF分量进行重构，得到新的合成信号；

d. 对合成信号求快速谱峭度图，根据谱峭度图来选择带通滤波器中的相关参数；

e. 根据谱峭度图确定带通滤波器的中心频率和带宽并进行带通滤波；

f. 对带通滤波器滤波后的信号进行平方包络处理和FFT变换；

g. 对处理后得到的特征频谱与滚动轴承故障特征频率进行比较，判断故障信息。

3.2工程应用

实验过程中，首先对采集信号进行CEEMD分解，分解得到14个IMF分量和一个残余项，由于滚动轴承故障信息集中在高频处，因此选取前7个IMF进行研究，IMF分量如图2所示。

实验数据来自于美国Case Western Reserve University轴承数据库。该实验台包括一个两马力(1英制马力=0.7455kW)的电动机、一个扭矩译码器和一个功率测试计。电动机的转轴由斯凯孚公司生产的SKF6205系列轴承端支撑，该轴承规格为：

滚动体个数 7个

图2 CEEMD分解

内圈直径 0.984 3mm

外圈直径 2.047 2mm

滚动体直径 0.312 6mm

节径 1.537mm

轴承采用电火花加工单点故障，损伤直径分别为0.007、0.014、0.021英寸(1英寸=2.54cm)，利用加速度传感器采集故障轴承的振动信号，加速度传感器位于电动机驱动端的轴承座上方，轴承外圈的损伤点分别位于3点钟、6点钟、12点钟3个不同位置，振动信号由16通道数据记录仪采集得到，采样频率为12kHz。

笔者采用电机转速为1 772r/min处的故障信息，损伤点为12点钟方向的轴承信号。该信号包络峰值小，一般不利于检查，由此能较好地验证笔

者所提方法的可行性。经计算该轴承外圈故障频率为105.87Hz。

IMF分量对应的峭度值如图3所示。选择峭度值大于3的IMF分量进行重构，重构信号如图4所示。由图4可知：经重构后的滚动轴承故障信号比原信号具有更高的信噪比。

图3 各IMF分量对应的峭度值

图4 重构信号

将重构信号进行谱峭度分析，其快速峭度图如图5所示。图像颜色的深浅代表不同频率f和频率分辨率Δf下的谱峭度值。由图5可知最大谱峭度值对应的分解层数为3。将这些参数作为检测滤波器的参数，由此可得，带通滤波器的中心频率取4 875Hz、带宽取750Hz进行带通滤波。

经带通滤波处理后的包络检波波形如图6a所示，图6b为对包络波形进行快速傅里叶变换形成的包络谱。从图中可以清楚地找到故障特征频率为106Hz。

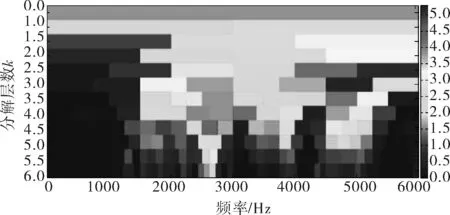
图5 重构信号的快速谱峭度图

图6 包络谱图

4 结束语

采用CEEMD法对滚动轴承信号进行分解。由于峭度值是判断电机故障与否的重要指标，因此将分解后的信号依次求取峭度值不仅能有效剔除滚动轴承故障信号分解后的伪分量，而且能提高故障信号的信噪比。选取峭度值大于3的信号进行重构，对重构信号进行谱峭度分析，通过峭度图选择带通滤波器的相关参数，有效地解决了共振解调中参数选择这一难题。采用美国西储大学公开的轴承故障数据作为实验数据来验证笔者提出的基于CEEMD与谱峭度结合的电机故障诊断的正确性，结果表明该方法能够有效地识别出滚动轴承的故障信息。

[1] 王豪，郑恩让.概率神经网络在电机故障诊断中的应用[J].化工自动化及仪表，2010，37(8)：59～62.

[2] 刘建文.基于共振解调与人工神经网络的轴承智能诊断技术研究[D].成都：西南交通大学，2007.

[3] 张涛，杨国安，周建军，等.离心式热油泵振动测试分析与故障诊断[J].化工机械，2011，38(6)：761～765.

[4] 陈宗衍，张森，杨国安，等.振动信号在电动机电气故障诊断中的应用[J].化工机械，2013，40(3)：383～386，395.

[5] Antoni J.The Spectral Kurtosis:A Useful Tool for Characterising Non-stationary Signals[J].Mechanical Systems and Signal Processing，2006，20(2):282～307.

[6] Huang N E，Wu Z H.A Review on Hilbert-Huang Transform:Method and Its Applications to Geophysical Studies[J].Reviews of Geophysics，2008，46(2)：11～23.

[7] Deering R,Kaiser J F.The Use of Masking Signal to Improve Emprical Mode Decomposition[C].IEEE International Conference on Acoustic，Speech,and Signal Processing.Philadelphia,USA：IEEE，2005:485～488.

[8] Wu Z H，Huang N E. Ensemble Empirical Mode Decomposition:A Noise Assisted Date Analysis Method[J].Advances in Adaptive Data Analysis，2009，1(1)：1～41.

[9] 王姣，李振春，王德营.基于CEEMD的地震数据小波阈值去噪方法研究[J].石油物探，2014，53(2)：164～172.

[10] 张明，曾庆军，眭翔，等.基于CEEMD的水下机器人MEMS陀螺降噪方法[J].传感技术学报，2014，27(12)：1622～1625.

[11] 蔡艳平，李艾华，石林锁，等.基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J].振动与冲击，2011，30(2)：167～172.

[12] 朱可恒.滚动轴承振动信号特征提取及诊断方法研究[D].大连：大连理工大学，2013.

[13] 赵妍，李志民，李天云.一种基于谱峭度的异步电机故障诊断方法[J].电工技术学报，2014，29(5)：189～196.

[14] 苏文胜.滚动轴承振动信号处理及特征提取方法研究[D].大连：大连理工大学，2010.

(Continued from Page 1035)

AbstractDCS’s control scheme and hardware configuration for sulfuric acid production were presented.Through discussing the furnace temperature control system based on InTouch and InControl, the feasibility of applying DCS to the sulfuric acid production was investigated to show that, both stable and reliable temperature control system has reference value for applying DCS in the sulfuric acid production.

KeywordsDCS, sulfuric acid process, furnace temperature control system, InTouch, InControl, PID

BearingFaultDiagnosisBasedonCEEMDandSpectralKurtosis

JIANG Jian-guo, LIU Ying-xuan

(CollegeofElectricalEngineeringandInformation,NortheastPetroleumUniversity,Daqing163318,China)

Considering the difficulty in selecting band-pass filter parameters when applying resonant demodulation in rolling bearing fault diagnosis, a bearing fault diagnosis method which having overall average empirical mode decomposition method (CEEMD) combined with spectral kurtosis method was proposed.The actual signals

verify the feasibility of this method.

bearing,fault diagnosis, CEEMD, spectral kurtosis

TH133.33

A

1000-3932(2016)10-1043-05

2016-09-09(修改稿)