圆柱刀五轴数控侧铣直纹面的直线插补误差分析
2016-11-22周雪梅曹利新大连理工大学
周雪梅 曹利新/大连理工大学
圆柱刀五轴数控侧铣直纹面的直线插补误差分析
周雪梅 曹利新/大连理工大学
0 引言
为解决CNC系统中复杂曲面的成型问题,相邻刀位点间运动由数控系统提供的插补功能完成。插补是通过对数据点的密化,不断趋近或逼近理论形体。目前,最常用的插补方法有直线、圆弧、样条插补,直线插补方法最具典型性。为提高直纹面侧铣加工精度和加工效率,众多学者对刀具包络面计算、插补方法误差及刀位规划方法进行了大量研究。朱利民[1]建立刀具包络面及第一和第二基本型的解析表达式,并给出了刀具包络面最佳逼近设计曲面的造型方法。吴大中[2]分析了五坐标数控系统线性插补的理论加工误差,建立了非线性误差估计模型。
Liu[3]提出适用于圆柱铣刀的单点偏置法和两点偏置法,方法简单,但计算误差大。GONG[4]提出了一种使刀具扫描面和工件曲面间相对法曲率最小化来实现加工带宽最大化的局部刀位优化算法。REDONNET等[5]提出了适用于圆柱刀侧铣加工的三点刀位规划方法,能有效降低加工曲面与刀具干涉,但计算复杂。葛荣雨等[6]利用最小二乘优化法确定侧铣加工直纹凸轮廓面的刀位计算。滕飞等[7]利用增量优化算法解决刀具轨迹的优化问题,实现了对多余刀位点进行的精简。Watkenti等人[8]提出了多点接触的刀位优化方法。朱利民等[9]通过优化刀具的前倾角和侧倾角使得在刀触点处刀具包络曲面与设计曲面达到三阶切触,显著增大加工带宽。本文的刀位确定采用最佳一致逼近方法[10],该方法刀位规划误差明显小于两点偏置法、最小二乘刀位规划方法。
1 圆柱铣刀的线性插补运动
数控加工是复杂曲面最主要的加工方式。复杂曲面广泛应用于工程领域,是叶轮、叶片、凸轮等零件的功能设计曲面,针对实际中不同的应用需求,众多学者对相关曲面零件的曲面造型,结构优化,加工工艺,结构强度,性能等方面进行了大量研究,以满足工程需求[11-14]。复杂曲面主要包括自由曲面和直纹面。自由曲面是设计人员根据气体动力学原理,通过大量计算,得到的一组离散数据点,不能用严格的数学方程表示;而直纹面是指由一系列直线段沿空间两条曲线扫描而成的曲面[15]。
从刀具与曲面的接触方式来讲,曲面的五坐标数控加工有点接触成形和线接触成形两种方式。刀具在点接触成形时,切削过程中刀刃与被加工曲面始终保持相切于一点,由点汇成线,由线组成面,主要适用于自由曲面的切削加工;刀具在线接触成形时,其侧刃始终保持与被加工曲面间线接触加工,利用铣刀刀刃的母线在加工中形成的包络面来逼近曲面,更加适合用于加工本文研究的直纹面[16]。侧铣加工属于线接触加工成形方法,在五轴数控系统中直纹面的精加工主要采用侧铣的加工方式。
被加工形面的不可展性会引起原理性加工误差,因此合理优化刀具路径,对于减小加工误差、提高零件性能具有至关重要的作用,因此通过参考文献[10]中误差明显小于两点偏置法和最小二乘方法的最佳一致逼近方法对刀具位置进行确定,获得圆柱刀在五轴数控系统中侧铣非可展直纹面时的刀心位置以及刀轴矢量,并且在相邻两刀位点之间采用线性插补算法。在利用圆柱刀侧铣加工直纹面的过程,实际上就是使圆柱面尽可能接近设计曲面的过程,属于面与面的逼近问题,可以采用最小二乘法和最佳一致逼近等方法,由文献[10]可知,刀具曲面上的特征线与设计曲面间的单向Hausdorff距离最能体现圆柱刀与设计曲面的贴近程度。特征线与设计曲面的单向Hausdorff距离就是特征线上任意一点到设计曲面最小距离的最大值,具体最佳一致逼近法参考文献[10]。
利用最佳一致逼近方法得到刀具刀位点和刀轴矢量后,相邻刀位点间线性插补过程如图1所示,pi和pi+1分别为刀具位于第i与第i+1个刀心点的位置矢量,αi和αi+1分别是刀位点pi,pi+1对应的刀轴矢量。当刀具在任意两刀位点间进行线性插补运动时,机床的直线运动轴和回转轴将使刀具刀心位置从第个刀位点线性地移动到第i+1个刀位点的位置上。因此在pi、pi+1间任意一刀心点p的方程可表示为:
式中:为刀心点沿直线段pi,pi+1的线性运动的运动参数。
为保证线性插补过程中相邻插补点间刀轴矢量变化是均匀变化的,对刀轴矢量也进行线性插值,即确保在单位时间内矢量αi旋转变换到αi+1的角度增量值是相等的。设刀轴矢量αi与αi+1之间的夹角为θ;bi为在由刀心点pi、刀轴矢量αi与αi+1所张成的平面内并且与刀轴矢量αi垂直的单位矢量。
当相邻刀位点间刀轴矢量αi与αi+1不共线时,bi的矢量方程式可表示为:
此时,对应于插补点p的刀轴单位矢量方程可表示为
通过式(1)和式(2),可以得到pi,pi+1间任意线性插值点p处刀轴上任意一点Q的位置矢量方程
2 圆柱铣刀包络面的计算
刀具运动形成的包络曲面即为得到的加工曲面,由文献[17]可知,在给定刀具运动规律的前提下,回转面刀具的包络面可以归结到刀具轴线上来讨论。因此在利用圆柱刀侧铣加工直纹面时可以利用已知的刀具轴线,通过包络原理得到刀具面上的特征点,从而可以得到刀具包络曲面,即刀具切削运动形成的加工曲面。已知刀具轴线上一点Q的运动方向V,则对应于轴线上Q点的刀具包络面上的特征点E,在通过P点、沿α×V方向上与刀具曲面的交点。将式(4)或(5)对参数μ求导,可以得到
圆柱铣刀包络面上特征点E的方程可表示为
式中,r为圆柱铣刀的小端半径。
3 刀具线性插补引起的几何误差
由于数控系统本身的特点,在我们用到的插补方法中,无论是直线插补、圆弧插补还是样条插补,都是利用直线或圆弧对曲线进行逼近的方法。因此,在实际加工中刀具切削得到的几何形状很难与理想几何形状完全符合,这种刀具包络面与理想的被加工曲面之间的偏差,即代表由线性插补引起的几何误差。五轴数控加工的成形原理为单参数面族包络原理,实际加工误差为刀具包络面与设计曲面间的法向误差[1]。因此,线性插补引起的几何误差,通过设计曲面与刀具包络面之间的法向误差来衡量。
文献[18]研究了点到隐式曲面的最小距离。并利用离散的牛顿迭代法求取方程组的解,以此得到点到曲面的最小距离。文献[19]在此基础上利用正交投影算法研究点到隐式曲面的最小距离,文献[1]定义两种用于评价设计曲面与包络曲面之问偏差的法向误差函数。基于此本文将求取刀具曲面特征点到被加工曲面的最小距离来得到柱刀线性插补的几何误差。
过刀具包络曲面上特征点E(li)做被加工曲面的垂线,垂足点为S(u*,v*),曲面S在Epi点的单位法矢为ni。对应于E(li)点的偏差为
式中,li为离散化的刀轴参数;u*,v*为特征点E(li)到被加工曲面垂足点所对应的曲面参数;单位法矢ni中i=1,2,3,…,m,m为任意一个刀位点上特征点的个数。
如果刀具曲面侵入到设计曲面实体之内,产生的误差称为过切误差;如果刀具曲面位于设计曲面接触,引起的误差称为欠切误差。若ε为正值,表示欠切;相反则表示产生过切。当对凸曲面或曲面的外凸部分进行线性插补时,ε为负值,会发生对曲面的过切现象;反之,当对凹曲面或曲面的内凹部分进行线性插补时,ε为正值,会发生对曲面的欠切的情况。
4 数值算例
本节通过两个数值算例验证前面所讨论模型和算法的正确性,在相邻两刀位之间通过CNC线性插值。
算例1:在直纹面侧铣刀位规划方法的研究中,经常需要选择同一算例,采用不同的方法进行研究,比较不同方法之间的优劣,其中文献[20]给出的直纹面因其特征明显,受到许多研究人员采用。该直纹面的方程式如下:
式中,c1(u)=ui+20.429j,c2(u)=ui+0.0382u2j+33.995k为直纹面的两条准线方程为直纹面的准线参数为直纹面的直母线参数;i,j,k分别表示坐标系{O-XYZ}三个坐标轴的单位矢量。由表达式可以看出,准线c1(u)为O-XY平面内一平行于X轴的直线,准线c2(u)为一平行于O-XY平面的抛物线。如图2所示,随着准线参数u的增大,直母线两端法线间的夹角Q也随之逐渐增大,即直纹面的扭曲加重。利用MATLAB软件实现直纹曲面造型如图3。采用直径20m的圆柱铣刀,按照文献[10]给出的最佳一致逼近方法对刀位进行规划。确定刀位时,在刀轴上均匀选择10个离散点参与计算,计算精度取10-8。
在直纹面准线参数域[0,23.014]内,均匀选择14个参数规划理论刀位,相邻刀位间采用线性插补均匀插入10个点,计算结果如图4a,其中圆圈为各理论刀位下的最大误差值、圆点为相邻刀位间线性插补点处的最大误差值。可以看出,由于采用线性插补,刀位点(圆圈)的前、后刀具的运动方向不同,导致刀位点处的误差曲线出现突变,而且随着直纹面扭曲程度的加重,突变更加严重。
为了减小由于理论刀位点处由于线性插补引起的突变误差,可以采取加密理论刀位点的办法。图4b,4c分别为在直纹面准线参数域[0,23.014]内,均匀选择29,59个理论刀位点的计算结果,相邻刀位间线性插补点的数量保持不变。由图可以看出,随着理论刀位点的增多,由于线性插补引起的误差迅速减小,剩余的误差为直纹面扭曲引起的刀位规划误差。
算例2.利用文献[21]给出的两条准线均为3次B样条曲线的直纹曲面,控制顶点如表1、表2所示,节点矢量为[0,0,0,0,0.2,0.4,0.6,0.8,1.0,1.0,1.0,1.0]。B样条曲线是利用控制点定义的,B样条曲线的方程为,其中di, i=0,1,2,…,n为曲线控制顶点,Ni,k(u)为k次B样条曲线的基函数。直母线两端法线间的夹角Q随准线参数的变化规律如图5所示。由图中可以看出,此直纹面的扭曲度变化不大,扭曲程度较算例1要小。利用MATLAB软件得到此直纹面的曲面造型,如图6。采用直径10mm的圆柱刀,按照文献[10]给出最佳一致逼近方法规划刀位。

表1 直纹面顶部线上控制点表mm
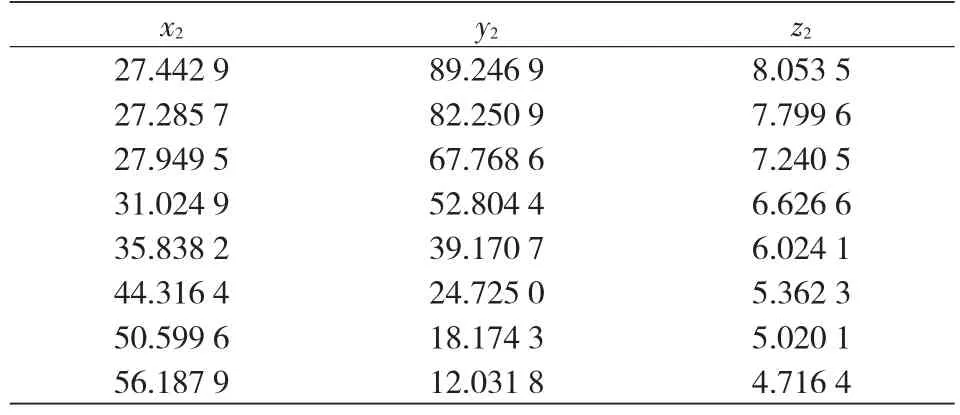
表2 直纹面顶部线上控制点表mm
在直纹面准线参数域[0,1]内,分别均匀选择14,29,59个参数规划理论刀位,相邻刀位间采用线性插补均匀插入10个点,各个刀位点处误差计算结果分别如图7所示,其中圆圈为各理论刀位下的最大误差值、圆点为相邻刀位间线性插补点处的最大误差值。由图可以看出,由于该算例直纹面的扭曲程度较小,曲面扭曲程度的大小并未造成线性插补刀位点处的误差曲线出现突变,但相邻刀位点间由于线性插补引起的误差较大,随着理论刀位点的增多,由于线性插补引起的误差迅速减小,而且在刀位点附近的几何误差比较小,两刀位点中间点处的误差较大。
5 总结
通过上述两个算例,对扭曲程度不同的两个直纹面利用最佳一致逼近方法规划刀位,在任意相邻刀位点间采用线性插补算法,得到刀具线性运动的包络曲面,利用包络面上特征点到设计曲面的距离计算由于线性插补引起的误差,通过对比发现:
1)尽管最佳一致逼近方法可以使单个刀位下的几何残留误差很小,但因相邻刀位点间的线性插补引起的误差依然需要重视,尤其是对于相邻刀位点间的距离或刀轴矢量间的夹角较大的情况。在两相邻刀位点间因线性插补引起的误差变化成近似抛物线分布,刀位点附近的几何误差小,两刀位点中间点处的误差大。
2)在刀具尺寸和刀位规划方法一定的情况下,直纹面侧铣的几何残留误差主要受直纹面的扭曲程度和刀位点间距离影响。随着刀位点数量的增多,由线性插补引起的误差迅速减小,剩余的误差主要是由直纹面扭曲引起的。因此,为了提高曲面加工精度,保证加工效率,要合理选取刀位点的数量以及刀位点的分布情况,降低非线性误差,提高直纹面侧铣精度。
[1]朱利民,卢耀安.回转刀具侧铣加工扫掠包络面几何造型及其应用[J].机械工程学报,2013,49(7):176-183.
[2]吴大中,王宇晗,冯景春.五坐标数控加工的非线性运动误差分析与控制[J].上海交通大学学报,2007,41(10):1608-1612.
[3]Liu X W.Five-axis NC Cylindrical Milling of Sculptured Surfaces[J].Computer-Aided Design,1995,27(12):887-894.
[4]H Gong,Fang FZ,Hu XT,et al.Optimization of Tool Positions Locally Based on the BCELTP for 5-axis Machining of Free-form Surfaces[J].Computer-Aided Design,2010,42(6):558-570.
[5]Redonnet DJM,Rubio W,Dessein G.Side Milling of Ruled Surfaces:Optimum Positioning of the Milling Cutter and Calculation of Interference[J].International Journal of AdvancedManufacturing Technology,1998,14(7):459-465.
[6]葛荣雨,冯显英,宋现春,等.空间凸轮廓面侧铣加工及最小二乘优化刀位方法[J].中国机械工程,2007,18(15):1842-1845.
[7]滕飞,闫光荣,简斌.采用增量优化原理的刀具轨迹优化算法研究[J].工程图学学报,2007,28(1):139-143.
[8]Warkentin A,Ismail F,Bedi S.Multi-point Tool Positioning Strategy for 5-axis Mashining of Sculptured Surfaces[J]. Computer Aided Geometric Design,2000,17(1):83-100.
[9]LM Zhu,H Ding,YL Xiong.Third-order Point Contact Approach for Five-axis Sculptured Surface Machining Using Non-ball-end Tools(II):Tool positioning strategy[J].Science China,2010,53(8):2190-2197.
[10]Cao L,Dong L.Positioning Method of a Cylindrical Cutter for Ruled Surface Machining Based on Minimizing One-sided Hausdorff distance[J].Chinese Journal of Aeronautics,2015,28(5):1564-1573.
[11]吴让利,吴沛佳,秦国良.叶片型线对离心风机性能影响的研究[J].风机技术,2014(1):31-36.
[12]许名珞.基于流固耦合仿真的小型轴流风扇优化设计[J].风机技术,2015(1):6-10.
[13]裴立群,魏国家,毕海波.直线轴联动铣制三元叶轮方法研究[J].风机技术,2013(2):49-51.
[14]唐俊,王军,刘辉.基于MATLAB的多翼离心风机参数化快速成型方法[J].风机技术,2015,57(2):42-47.
[15]金玉淑,贾莹,裴忠科.三元叶轮工艺方案分析[J].风机技术,2014(1):56-60.
[16]陈良骥,王永章.整体叶轮五轴侧铣数控加工方法的研究[J].计算机集成制造系统,2007,13(1):141-146.
[17]宫虎.五坐标数控加工运动几何学基础及刀位规划原理与方法的研究[D].大连理工大学,2006.
[18]余正生,樊丰涛,王毅刚.点到隐式曲线曲面的最小距离[J].工程图学学报,2005,26(5):74-79.
[19]方雄兵.点到隐式曲线、曲面的正交投影算法研究[D].华中科技大学,2008.
[20]Liu X W.Five-axis NC Cylindrical Milling of Sculptured Surfaces[J].Computer-Aided Design,1995,27(12):887-894.
[21]Ding H,Zhu L M.Global Optimization of Tool Path for Five-axis Flank Milling with a Cylindrical Cutter[J].Science in China,2009,52(8):2449-2459.
■在五轴联动数控系统中,相邻刀位点间的运动通过直线、圆弧或样条曲线进行插补运动,其中直线插补方法最具典型性。以圆柱刀侧铣加工直纹面时因线性插补引起的非线性误差为研究对象,首先,在被加工曲面上采用最佳一致逼近法规划圆柱刀侧铣直纹面的刀具位置;然后,利用包络原理建立刀具线性插补时所形成的包络面解析表达式;以理想曲面为基准面,利用牛顿迭代法求取点到曲面的最小距离,从而建立刀具包络面与理论曲面的误差模型,以此得到刀具线性插补时产生的非线性误差;最后,利用MATLAB软件通过数值算例对影响非线性误差的规律、大小以及其影响因素进行了分析。
■线性插补;非线性误差;侧铣;包络原理;最佳一致逼近方法
Linear Interpolation Error Analysis for Cylindrical Cutter of Five-axis CNC FlankMilling Ruled Surface
Zhou Xue-mei,Cao Li-xin/School of Mechanical Engineering,Dalian University of Technology
Linear,circular,and spline interpolation are used for interpolation motion in the five-axis CNC system,and the line interpolation method is most typical one. Aiming at the nonlinearerrorsdue to the linear interpolating during the rule surfaces flank milling by using cylindricalmilling cutter,the cutterposition and orientationwere determined by using the best uniform approximation method firstly.Then,the cylindrical cutter's envelope surface which was generated by cutter's linear interpolation motion between adjacent cutter location pointswas builded by the envelope principle.The nonlinear errors between the envelope surface and designed surface were obtained based on theminimum distance calculation between a point of envelope surface and the designed surface by using Newton iteration method.The pattern,scale and influence factors of the nonlinear errorwere analyzed via numericalexamplesby MATLABsoftware.
linear interpolation;nonlinear error;flank milling;envelope theory;best uniform approximationmethod
TH164;TK05
A
1006-8155(2016)04-0068-06
10.16492/j.fjjs.2016.04.0036
2016-04-21辽宁大连116024
