负荷对整体齿轮增速式离心压缩机转子系统动力学特性的影响研究*

丁端 王维民 刘宾宾 姜兴安/北京化工大学

负荷对整体齿轮增速式离心压缩机转子系统动力学特性的影响研究*

丁端 王维民 刘宾宾 姜兴安/北京化工大学

0　概述

整体齿轮增速式离心压缩机因其具有高效率、低能耗、结构紧凑、长期平稳运行等特点，近年来在全球范围内迅猛发展［1］。齿轮是整体齿轮增速式离心压缩机中传递运动和动力的关键部件，也正是由于齿轮的啮合作用使得齿轮-转子-轴承系统振动特性与单转子系统有着显著区别，即系统中存在弯扭耦合振动［2］。

路金昌［3］、戴继双［4］根据齿轮副运动微分方程得到齿轮啮合刚度矩阵，并对整个耦合系统进行固有特性分析。张义民［5］也基于此啮合刚度矩阵，对某膨胀机子系统进行瞬态不平衡响应分析。Stringer［6］研究出较为精确的12×12阶齿轮啮合刚度矩阵，崔津［7］根据此啮合刚度矩阵对某4轴6级整体齿轮增速式离心压缩机耦合转子系统进行了固有特性及不平衡响应分析。目前，学者们除了对齿轮-转子-轴承系统的固有特性以及不平衡响应分析做了大量研究外，还对齿轮-转子-轴承系统的非线性特性研究较多［8］，但很少有关于负荷对齿轮-转子-轴承系统动力学特性影响的研究。Zhang Hao［9］以某5轴5级整体齿轮增速式离心压缩为研究对象，研究负荷对耦合系统动力学特性的影响，但文中的轴承动力系数没有考虑到因齿轮啮合力而产生的交叉刚度、交叉阻尼系数。

本文以某4轴6级整体齿轮增速式离心压缩机组［7］为研究对象，首先求得工作转速下轴承载荷与负荷之间的关系，进而研究工作转速下负荷对齿轮-转子-轴承系统动力学特性的影响。

1　齿轮-轴承动力学分析

1.1齿轮-轴承载荷计算

齿轮-转子-轴承系统在升速达到工作转速后，处于不断提升负荷直至满负荷运转的过程。由于齿轮-转子-轴承系统是空间布置的，因此各个齿轮轴上的轴承所受载荷除与齿轮轴自重有关外，还与齿轮轴转速、方位角、齿轮节径、齿轮级间功率、轴承距齿轮中心跨距有关。通过DyRoBeS软件中GearLoad模块，计算主动齿轮轴1 500r/min转速下、耦合系统15 000kW满负荷时各齿轮轴上的轴承载荷及载荷角大小，其中GearLoad模块中的计算参数如表1所示，计算结果如图1所示。

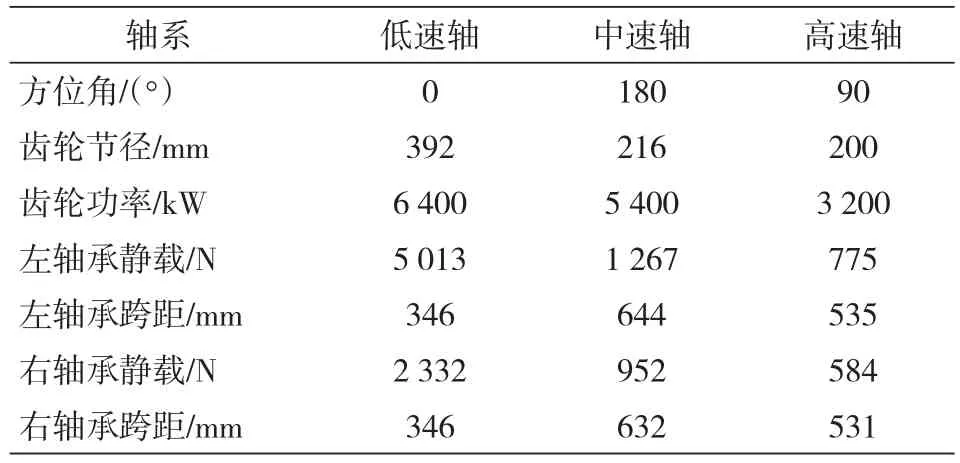
表1　齿轮-轴承载荷计算参数表

通过改变齿轮负荷功率大小，计算得出不同负荷时各齿轮轴上的轴承载荷及载荷角大小，并绘制轴承载荷及载荷角大小随负荷增大的变化曲线，如图2和图3所示。

从图2可知，当负荷增大至20％后，各个轴承的载荷大小随负荷增大而增大并呈线性关系。当负荷增大至40％时，低速轴上的轴承载荷开始大于静载时的轴承载荷。由于各齿轮轴方位角不同，低速轴与中速轴上的轴承所受载荷远大于高速轴轴承所受载荷。

从图3可知，随着负荷不断增大，当负荷增大至20％后，轴承载荷角逐渐趋于稳定。本文所研究的齿轮-转子-轴承系统中的低速、中速、高速轴上的轴承均为五瓦可倾瓦轴承，轴承瓦块采用瓦间载荷（LBP）排布。

增大负荷对齿轮-转子-轴承系统动力学特性影响的主要因素体现在轴承的刚度系数、阻尼系数的改变，轴承动力系数的改变会对齿轮-转子-轴承系统动力学特性产生较大影响。

通过给定不同的轴承载荷大小及载荷角，利用DyRoBeS中BePerf模块，根据表2中轴承参数（同一齿轮轴上轴承参数相同），计算得到各齿轮轴工作转速下的轴承刚度、阻尼系数随负荷增大的变化曲线。因各齿轮轴上的轴承刚度、阻尼系数随负荷变化规律基本相似，故仅列出中速轴上的左轴承刚度、阻尼系数随负荷增大的变化曲线，如图4所示。

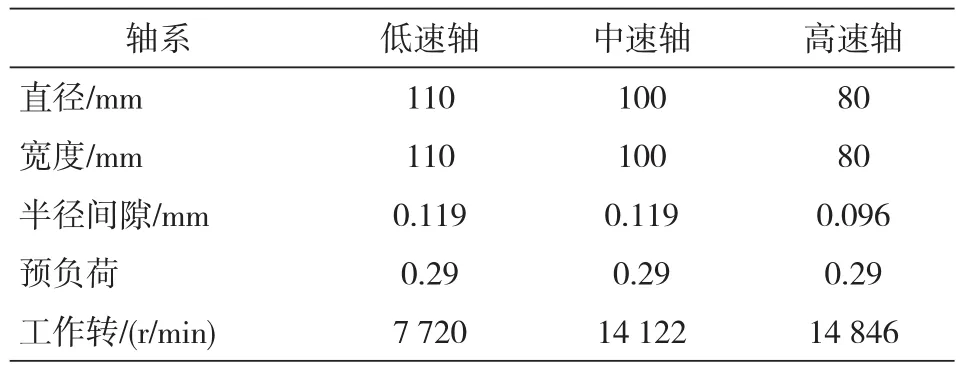
表2　各齿轮轴轴承参数表

1.2齿轮-转子-轴承系统有限元模型

美国石油标准学会的API672标准中将齿轮-转子-轴承系统中的各根齿轮轴转子人为分离并分别对单根齿轮轴转子进行动力学特性分析，而且许多大型压缩机制造商也仅仅是对各单根齿轮轴转子进行设计和分析，而未涉及耦合系统的固有特性及不平衡响应分析。

齿轮-转子-轴承系统运动微分方程为：

其中，M代表系统质量矩阵；C代表系统阻尼矩阵；K代表系统刚度矩阵；G代表系统陀螺矩阵；Ω代表转速；F代表力；X代表位移。

本文通过Ansys有限元软件对该齿轮-转子-轴承系统进行有限元建模，图5为该耦合系统有限元模型。在该有限元模型中，用Beam188单元模拟齿轮轴；用Mass21单元模拟齿轮轴上的集中质量（叶轮、齿轮、密封）、直径转动惯量和极转动惯量；用COMBI214单元模拟轴承，其中数值大小由1.1节中BePerf模块计算得出；用Matrix27单元模拟齿轮啮合刚度，矩阵采用Stringer［6］开发的齿轮啮合刚度矩阵，齿轮参数如表3所示。

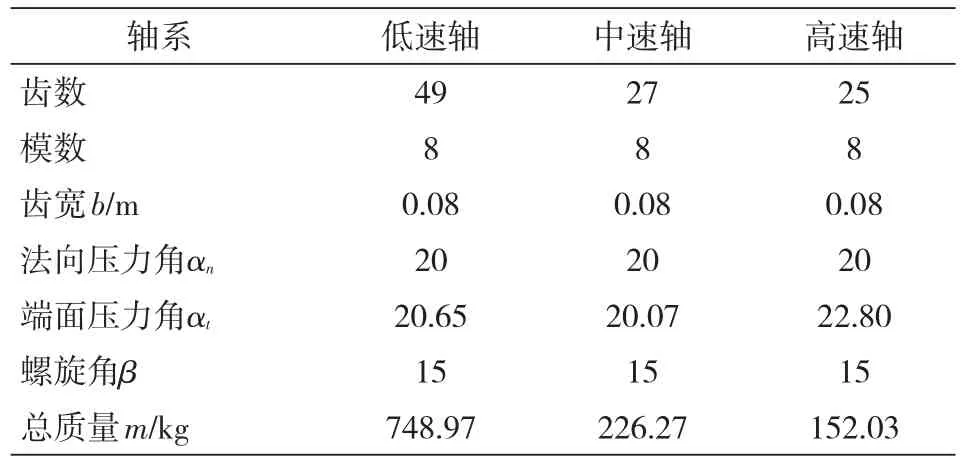
表3　各齿轮参数表

2　齿轮-转子-轴承系统模态分析

2.1耦合系统模态成分

整体齿轮增速式离心压缩机与单转子离心压缩机动力学特性差异较大，齿轮啮合使得耦合系统中含有多种模态成分，不仅含有未耦合时单轴的弯曲模态，同时还含有新耦合出来的单轴弯扭耦合模态、多根轴的弯扭耦合模态。

2.2负荷对耦合系统模态频率的影响

为研究负荷对耦合系统模态频率的影响，本文以工作转速下20％负荷为起始，每次增加10％负荷直至满负荷，对齿轮-转子-轴承系统进行模态求解分析。将单轴弯曲模态频率整合，并绘制单轴弯曲模态频率随负荷增大的变化曲线，如图6所示。

其中，ωi，j中i=1，2，3分别代表低速、中速、高速轴；j=1，2代表第一阶、第二阶弯曲模态频率。从图中可以看出，单轴弯曲模态频率随着负荷增大而增大，但增幅较小。在提升负荷的过程中，各单轴弯曲模态频率没有与其各自的激振频率相交。采用相同方式，绘制单轴弯扭耦合模态频率、多轴弯扭耦合模态频率随负荷增大的变化曲线，如图7、8所示。

图7为齿轮耦合而出的单轴弯扭耦合模态频率随负荷增大的变化曲线。从图中可知，随着负荷不断增大，耦合出来的单轴弯扭耦合频率也随之增大，且增幅较大，其中低速轴的第二阶弯扭耦合频率与低速轴的激振频率Ω1相交于75％负荷处，中速轴的第一阶弯扭耦合频率与中速轴激振频率Ω2也相交于75％负荷处，这说明了齿轮-转子-轴承系统中可能会存在临界负荷。如果设计不当，满负荷工作下的模态频率与系统激振频率相同或相近时，在不平衡力以及气流激振力作用下，转子系统会持续产生较大的振动，严重时可能会对压缩机组造成破坏。

从图8中可知（ω1、ω2为多轴第一阶、第二阶弯扭耦合频率），因齿轮耦合而出的多轴弯扭耦合模态频率随负荷增大而增大，这与单轴弯曲模态频率、单轴弯扭耦合模态频率的变化规律相似。但多轴弯扭耦合模态频率远离系统的激振频率，所以对耦合系统工作转速下不断增大负荷过程中的振动特性影响不大。

3　齿轮-转子-轴承系统不平衡响应分析

API672中附录C关于临界转速和阻尼不平衡响应计算规定的内容，是对齿轮-转子-轴承系统中各单根齿轮转子进行不平衡响应分析。本文根据此标准内容，确定施加于各根齿轮轴转子上的不平衡量大小及相位。

2.2节中的中速、高速轴弯曲模态频率虽与低速轴激振频率相交，但未与其各自的激振频率相交。对未耦合时的各齿轮轴转子从20％负荷增至100％负荷的过程进行不平衡响应分析，研究发现随着负荷增大，工作转速下的轴承处振动幅值减小。这说明未耦合时系统中没有出现临界负荷，也证实了模态分析中单轴弯曲模态频率没有与其各自激振频率相交的结论是正确的。

低速轴、中速轴的弯扭耦合频率与其各自激振频率相交，所以首先分别对耦合系统中低速轴、中速轴施加不平衡量来观察其不平衡响应。但由于耦合系统中存在齿轮啮合作用，系统振动可能呈现出传递的特性，所以同样需要对耦合系统高速轴施加不平衡量来观察高速轴的振动特性。不平衡量施加的位置、大小、相位如表4所示。

图9为分别对耦合系统中的低速轴、中速轴、高速轴两端叶轮处施加不平衡量后计算得出的其各轴上的轴承处振动幅值随负荷增大的变化曲线。

从图中可知，在工作转速下，随着负荷不断增大，当负荷增至80％时，低速轴、中速轴、高速轴上的左右轴承处均出现振动峰值。低速轴、中速轴上的轴承处振动出现峰值，能够证实2.2节中75％负荷时齿轮-转子-轴承系统耦合出来的单轴弯扭耦合频率与其各自激振频率相交是存在的，同时说明了耦合系统在增加负荷的过程中出现了临界负荷。在模态频率分析中，虽然高速轴模态频率没有与高速轴的激振频率相交、也不相近，但高速轴上的轴承在80％负荷时出现振动峰值，这是受低速轴、中速轴模态频率与激振频率相交的影响，同时也说明了齿轮-转子-轴承系统中各根转子之间存在振动传递的特性。

由于低速轴上左叶轮的质量与右叶轮的质量有较大差异，左叶轮惯性较大，而左右叶轮处所施加不平衡量大小相同，所以出现了低速轴上的右轴承处振动幅值大于左轴承处振动幅值的现象。由于齿轮-转子-轴承系统中各根齿轮轴转子之间存在振动传递的特性，致使高速轴上的右轴承处振动幅值也大于左轴承处振动幅值。

因此在设计分析整体齿轮增速式离心压缩机时，除了需要对未耦合时单轴不平衡响应进行分析外，还需要计算工作转速下不断提升负荷过程中的不平衡响应，找到临界负荷点，以避免系统满负荷工作点处于临界负荷点附近，避免系统持续较大振动。

4　齿轮-转子-轴承系统稳定性分析

转子动力学中通常将对数衰减率作为评判系统是否稳定的主要因素，并要求转子系统的第一阶正进动模态频率所对应的对数衰减率大于0.1。本节根据2.2节中对模态求解所得到的特征值计算出与图6～图8中共14阶固有频率相对应的对数衰减率并绘制对数衰减率随负荷增大的变化曲线，结果如图10～图12所示。

从图10可知，工作转速下单轴弯曲模态频率所对应的对数衰减率随负荷增大而减小，虽然在100％负荷时最小值仍大于0.1，齿轮-转子-轴承系统仍处于稳定状态，但很有可能会因设计不当而出现负荷增大时对数衰减率小于0.1的现象，造成耦合系统失稳。

从图11可知，耦合出的低速轴第一阶弯扭耦合频率与高速轴弯扭耦合频率对应的对数衰减率随负荷增大而减小，但最小值仍大于0.1，而其它对数衰减率随负荷增大而增大。

从图12可知，多轴弯扭耦合频率所对应的对数衰减率随负荷增大而增大，对耦合系统稳定性影响不大。

5　结论

本文研究成果可为整体齿轮增速式离心压缩机的设计提供技术支持。对整体齿轮增速式离心压缩机进行转子动力学分析时，不仅要考虑升速过程中的固有频率变化以及过临界时的振动峰值大小，同时需要考虑工作转速下提升负荷过程中的模态频率变化及轴承处的振动峰值大小。通过以上分析，获得如下结论：

1）整体齿轮增速式离心压缩机工作转速下随着负荷增大，其模态频率会随之增大，单轴弯扭耦合频率的增幅较大并与激振频率相交。

2）在增大负荷的过程中轴承处出现临界负荷点，产生振动峰值。单轴弯扭耦合频率对耦合系统的振动具有传递特性。

3）在增大负荷的过程中，单轴弯曲频率所对应的对数衰减率随之减小，弯扭耦合频率所对应的对数衰减率部分随之增大、部分随之减小。如果设计不当，很有可能出现随着负荷增大，对数衰减率小于0.1的现象。

［1］成正朝，牛大勇.组装式离心压缩机的特点及发展趋势［J］.风机技术，2003（4）：3-5.

［2］Maurice L.Adams.Rotating Machinery Vibration-From Analysis to Troubleshooting［M］.Taylorand FrancisGroup，New York，2010.

［3］路金昌，王一.多轴齿轮耦合转子系统的振动分析［J］.机械传动，2013（9）：118-121.

［4］戴继双，马辉，李朝峰，等.含增速齿轮的转子系统固有特性研究［J］.东北大学学报（自然科学版），2011（9）：1299-1303.

［5］张义民，何永慧，朱丽莎，等.多平行轴齿轮耦合转子系统的振动响应［J］.振动、测试与诊断，2012（4）：527-531.

［6］D.B.Stringer，P.N.Sheth.Geared rotor dynamic methodologies for advancing prognostic modeling capabilities in rotary-wing transmission systems［D］.The faculty of the School of Engineering and Applied Science：University ofVirginia，2009.

［7］崔津，王维民，高金吉，等.多平行轴系离心压缩机振动耦合传递特性研究［J］.流体机械，2013（12）：10-15.

［8］谭秀峰，张国伟，谢里阳，等.齿轮传动系统的动力学研究与展望综述［J］.机电工程，2014（5）：559-562，577.

［9］Zhang Hao，Zhai Jingyu，Han Qingkai，et al.Dynamics of a geared parallel-rotor system subjected to changing oil-bearing stiffness due to external loads［J］.Finite Elements in Analysis and Design，2015.

■整体齿轮增速式离心压缩机振动特性较单转子压缩机更为复杂，由于存在齿轮啮合作用，齿轮-转子-轴承系统耦合出新的频率、振动峰值。本文以一台在役的4轴6级整体齿轮增速式离心压缩机为研究对象，建立齿轮-转子-轴承系统的弯扭耦合有限元模型，分析在工作转速下不断提升负荷过程中耦合系统的动力学特性。模态分析表明：随着负荷增大，耦合频率中的单轴弯扭耦合频率增幅较大，并在75％负荷时与激振频率相交；不平衡响应分析表明：随着负荷增大，在80％负荷时出现临界负荷点，轴承处出现振动峰值。稳定性分析表明：随着负荷增大，单轴弯曲频率所对应的对数衰减率降低，单轴弯扭耦合频率所对应的对数衰减率部分增大、部分降低，多轴弯扭耦合频率所对应的对数衰减率增大。

■齿轮啮合；耦合频率；不平衡响应；临界负荷；对数衰减率

The Research of the Rotor System Dynam ics of an Integrally Geared CentrifugalCompressor Due to External Loads

Ding Duan，Wang Wei-min，Liu Bin-bin，Jiang Xing-an/Beijing University of Chemical Technology

The vibration characteristics of an integrally geared centrifugal compressor are more complex than a single-rotor compressor，due to the gearmeshing，a gear-rotor-bearing system couples to new frequencies and the vibration peaks.In this paper，a four-axis and six stages integrally geared centrifugal compressor was taken as the research object，and the bending and torsion coupling finite element model of the gear-rotor-bearing system was established.The dynamics characteristic of thesystem wasanalysedwhen the external loads are increasing under the operating speed.Modalanalysisshows thatwith the load increasing，the bending and torsion coupling frequencies of the single-rotor increase a lot，and intersectwith the excitation frequencies at 75％load point.Unbalance response analysis shows that with the load increasing，the critical load point emerges when the load is 80％and the bearings occur peak vibrations.Stability analysis shows that with the load increasing，the corresponding logarithmic decrement rates of the single-rotor's bending frequencies decrease，the corresponding logarithmic decrement rates of the single-rotor's bending and torsion coupling frequencies decrease partly and the others increase，the corresponding logarithmic decrement ratesof themulti-axialbendingand torsion coupling frequenciesincrease.

gear meshing；coupling frequency；unbalance response；critical load；logarithmic decrementrate

TH452；TK05

A

1006-8155（2016）04-0022-06

10.16492/j.fjjs.2016.04.0041

国家自然科学基金重点项目（51135001）；北京高等学校青年英才计划（YETP0495）

2016-04-15北京100029