现代教育技术在中学数学教育中的应用

张俊忠+肖宏治

【摘要】数学教育中既要讲演绎又要讲归纳，有了现代教育技术，数学教学不再局限于演绎推理，可以顺畅地引导学生观察、类比、归纳、猜想、概括和推理，去领悟数学的真谛。运用现代教育技术，不但能够帮助教师进行研究性教学，促进学生开展研究性学习，而且有利于培养学生的创新精神。

【关键词】问题情境 发散思维 动画技术 数学实验

【基金项目】贵州师范学院社会科学研究基金项目（2015BS016）的阶段性成果。贵州省2014年省级本科教学工程项目（黔教高发[2014]378号）的阶段性成果。

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2016）09-0202-02

当今世界，信息化已经成为经济和社会发展的大趋势。现代信息技术极大地拓展着教育的时空界限，改变着教与学的关系。数学教育家玻利亚指出：“数学有两个侧面，一方面是欧几里德的严谨科学，从这个角度看，数学像一门演绎科学；但另一方面，创造过程中的数学看起来像一门实验性的归纳科学。”数学的抽象性和经验性，决定了数学教育中既要讲演绎又要讲归纳。运用现代教育技术，能够帮助教师进行研究性教学，促进学生开展研究性学习。本文主要介绍现代教育技术在中学数学教育中五个方面的应用。

一、创设问题情境，为探索式教学提供便利的条件

中学阶段，是学生智力因素迅速发展，非智力因素逐渐形成和趋于稳定的关键时期。要使非智力因素在教学活动中发挥积极的作用，情境教学是一条有效的途径。问题是数学的心脏，“问题解决”的能力是数学能力的集体体现。探索式教学强化“问题意识”，它要充分展现问题的加工处理过程、解决方案的制定过程，这样既能磨炼学生的意志品质，也能培养学生解决问题的能力。[1]运用现代教育技术，这个探索的过程能在课堂上高效、快捷地进行。

如在进行初中“不在同一直线上的三个点确定一个圆”这个定理的教学时，运用探索式教学模式，可以设计如下：

提供问题：学校实验室里某种仪器的一块圆形玻璃打破了（同时配上打碎的声音），有一块残片如图1，请你帮助配一块和原来完全相同的圆形玻璃。用Powerpoint软件把这个问题和图形展现出来，其它各步骤讨论完之后，再展现完整的过程，这样既节约了时间，同时形象、直观，调动了学生学习的兴趣。

还有在讲《绝对值几何意义的应用》这一研究课时，一上课可以用Powerpoint软件展示一个问题：当x取何值时，y=|x+4|+|x+2|+|x+1|+|x-3|有最小值（请在3分钟内解决）。这个问题的提出，一下子就能抓住学生的目光，干脆利落，使学生马上进入探索的氛围中。显然学生刚开始一下子很难解决这个问题，过了2分钟后，教师马上说这个问题对大家现在来说比较困难，但通过这节课的学习，绝对有学生在1分钟之内能解决。一下子学生们带着期盼的心情进入下一阶段的学习，总之，运用现代教育技术，使创设问题情境更方便，快捷。

二、营造发散机会，为研究性学习建立宽松的环境

在数学教育中运用和注重发散性思维，能够促进教师创建良好的教育情景。比如教师可以用一题多变、一题多解、一法多用等方式展现问题，充分激发学生的兴趣和好奇心。[2]如果学生是在教师的主导下以主动的状态去学习，那么学生的思维就会很活跃，学生就能够自如地展示自己。当学生的有意知觉和无意知觉处于和谐状态时，就能够创建最融洽的课堂氛围，因而能够产生最有效的教育效果。[3]在数学学习中，一个问题有多种解法是很普遍的。

特别是几何题，有时画图很不方便，运用现代教育技术，画图显得轻而易举。这样在课堂上就能够充分倾听学生的想法，启发学生各抒己见，评判各方面的优劣，选出公认的最佳方法，从而造就了民主的课堂气氛。

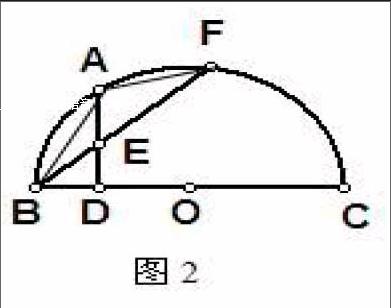
例1：如图2，BC是⊙O的直径，AD⊥BC于D，AB=AF，BF交AD于E，求证：AE=BE

此题可以启发学生从三个方面考虑，找到至少六种解法。对于学生的每一种解法，教师都要给予充分的肯定，这样能够增强学生学习的信心。再通过比较，找到最优方法，提高学生的鉴别能力。在探究的过程中，利用“超级画板”软件，图画得快、清晰，将起到促进作用。

例2 ：如图所示，等腰△ABC，AB=AC，O为△ABC的外心。如图3，当P、Q分别为AB、AC的中点时，连接OP、OQ、PQ，求证：∠BAC=2∠PQO

在直接证明原问题后，可以利用“超级画板”软件，探索改变题目的条件，使图形发生变化，在运动变化中观察相关图形的变化，找出隐含的不变性质，从中发现规律，比如：

变化1：如图4，当P、Q分别为AB、AC上的点且BP=AQ时，连接OP、OQ、PQ，此时是否也有∠BAC=2∠PQO？

变化2：如图5，如当P、Q分别为AB、CA延长线上的点且BP=AQ时，连接OP、OQ、PQ，此时∠BAC=2∠PQO是否成立？完成图5并证明你的结论。

探索后不难发现，上述两个经延拓后的新命题，仍然是真命题。

运用现代教育技术，在课堂上能够增加很多发散机会，能够为学生提供广阔的思考空间，从而能够充分展示学生的思维过程，调动学生的积极性。通过交流，集中群体的智慧，能实现课堂教学的“群英会” 、“大合唱”。

三、运用动画技术，开发学生思维

课改后中学数学教育的一个重要任务是培养学生的抽象思维能力，但是人们的思维过程往往是先具体再抽象，即从很多不同事物中概括出本质，再进行推理论证。[4]故在中学数学课堂中，教师要充分展示知识的产生过程，让学生从直观出发，通过大量的现象，体会和感悟其中的本质，逐步培养学生的抽象思维能力。而利用现代教育技术，能够将数与形有机地统一起来，能够将动态变化的过程具体生动地展现出来，这样能够促进学生由具体的认识升华为抽象的概括，因而有利于开发学生的思维，提高学生的综合能力。

如在学习初中《直线和圆的位置关系》时，可以首先用计算机展示如右图所示的直线和圆（静态的），然后跟学生们说，教师要做一个数学实验，让直线慢慢向上平移，请同学们观察直线在平移过程中与圆的位置有怎样的变化。于是教师可以用事先设计的，利用Powerpoint软件的动画功能，让直线慢慢向上平移。这个过程很形象、直观，通过几次演示，同学们能够清晰地抽象概括出直线和圆的三种位置关系，并且还能够说出每种状态下的特征。又如在学习圆周角定理的证明时：已知：∠BOC，∠BAC分别是弧BC在⊙O中所对的圆心角和圆周角，求证：2∠BAC=∠BOC

该证明要分如图三种情况，这是本节课的难点。如果孤立看成三个问题，会造成学生的认识困难。而在“超级画板”中，只要画好一个图形，然后移动A点的位置，就可以得到上面的三种情况是在同一条件下的三种位置状态，这样就能够直观地说明三者之间的联系，从而学生更容易理解问题的本质。

四、把实验引入数学课堂

在数学研究中，数学家往往需要反复实验才能发现规律，然后才是进行严格的逻辑推理和论证。在学校课堂教学中，如果教师传授知识重结果，轻过程；重理论描述与论证，轻实验和直观展示，那么学生将变成知识的容器，这样不利于培养学生研究问题和解决问题的能力。数学的学习过程不应该是重复记忆、被动吸收，反复训练的强化过程。一切新知识，只有通过学生自己的再创造，使其纳入学生自己原有的认知结构中，才能够成为活的有效知识。在学习过程中，如果能够创设合理的探索问题的情境，能够创设学生自由思维的活动空间，他们就能够在研究和解决问题中掌握知识，提高能力。[5]也只有这样，学生收获的才是数学经验，而不仅仅是一些数学结论。

例如在讲《三角形内角和》这部分内容时，首先，创设一种情景，激发学生内在求知的欲望。然后，让学生利用“超级画板”画一个三角形，并利用“超级画板”的计算功能得到三角形的内角和，然后再让学生交流结果，形成感性认识。在此基础上，老师还可以利用教育软件的动画功能，使三角形三个角通过平移和旋转构成一个角。至此，学生对三角形内角和为180°已经了形成确定无疑的感性认识。最后的问题是利用已有的知识去推理论证得到这个结论。教师再指导学生通过讨论交流，探索推理过程。此时教师可以适时启发和点拨，由学生自己完成分析和证明。在以上过程中，以“超级画板”为工具，让学生做数学实验，动手实践、亲自操作经历了知识的生成和知识的构建过程，这样获得的知识必然是深刻的、牢固的。“超级画板”所创造的学习过程的快捷性、形象性和生动性必然会给学生留下极为深刻的印象，这样进一步强化了学习的积极性和求知欲望。

五、运用网络，拓展视野

基于网络环境的中学数学课堂选择的学习素材，不仅可以是直接的数学问题，而且也可以是其它各种学科的问题。学习素材往往都有一定的背景，学生可以通过网络收集和整理有关材料，对材料进行分析、研究、对比，通过观察、实验、讨论、猜测、归纳、最后推理论证，这样不仅能拓展学生的视野，而且能够充分提高学生的综合能力。现代教育，教师不再是主要的信息源，教师是教学活动中的主导者，设计者和帮助者。学生是教学活动的主体，是知识的探究者。教师要帮助学生在学习过程中学会合作、学会组织、学会思考、学会交流，因此课堂教学的研究性要更加突出。授人以鱼，不如授人以渔；授人以渔，不如授人以渔场，应用现代教育技术更容易为学生创造一个宽大的渔场。利用现代教育技术来创设情景，提供不同的学习资源，让学生在观察情景的背景下，提出问题，分析问题，解决问题，从而更好地实现研究性学习。例如在高中讲到祖暅原理、杨辉三角等知识时，可以要求学生在网上查阅有关知识，并互相交流、讨论。同时经常要求学生在网上了解一些数学家的生平和有关数学史的知识，这样不仅能培养学生研究性学习的能力，而且能够增强学生学习数学的主动性、趣味性、生动性。

总之，现代教育技术应用到中学数学教育中去是当代数学教育发展的一种趋势，充分发挥现代教育技术的优势，可以使老师的教育教学手段显得更加的丰富多彩。通过对现代教育技术的合理选择和优化组合，将能够提高中学数学的教育质量，最终达到提高学生整体素质的目的。

参考文献：

[1]张丽晨、刘显国.初中数学课堂教学艺术[M]北京：中国林业出版社，2004.

[2]戴再平、孙联荣、凌国华、时晨.数学开放题研究[M].南宁：广西教育出版社，2012.

[3]毓郑信.数学教育：从理论到实践[M].上海：上海教育出版社，2001.

[4]靳玉乐.新课程改革的理念与创新[M].北京：人民教育出版社2003.

[5]杨雪男.中学生数学发散思维能力研究[D].南京：南京师范大学，2006.