大规模MIMO系统中低复杂度的稀疏信道估计
2016-11-20方昕刘云驹曹海燕潘鹏
方昕,刘云驹,曹海燕,潘鹏
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
大规模MIMO系统中低复杂度的稀疏信道估计
方昕,刘云驹,曹海燕,潘鹏
(杭州电子科技大学通信工程学院,浙江 杭州 310018)
针对大规模多输入多输出(MIMO)系统信道估计算法复杂度高的缺陷,结合无线通信信道固有的稀疏性提出了一种低复杂度的稀疏信道估计算法。该算法是在传统的离散傅里叶变换(DFT)信道估计的基础上利用分离算法将信道抽头与噪声空间分离开来,使得信道估计时只需要计算信道抽头的部分,因此算法的计算复杂度被大大降低。仿真结果表明,该算法在保持低复杂度的同时,可获得接近最小均方误差(MMSE)性能。
大规模MIMO;信道估计;稀疏性;算法复杂度
1 引言
大规模MIMO(multiple-input multiple-output)技术[1]是下一代移动蜂窝网的关键技术之一[2],它通过在小区基站端配备大量的天线形成大规模的天线阵列,充分利用空间资源大幅度地提升了信道容量和频谱利用率,成为了近几年来无线通信领域的一个研究热点[3-6]。在大规模MIMO系统中,一条精确的信道状态信息是至关重要的,直接关系到系统的信号检测、波束成形、资源分配等。而大规模MIMO系统中基站天线数目达到了成百上千级别,大大地加深了系统数据处理的复杂度,因此为了充分利用大规模MIMO技术潜在的优势,更加有效且复杂度低的信道估计算法值得进一步研究。
目前依据大规模MIMO系统各方面的特性,对大规模MIMO系统信道进行估计的算法很多。比如基于数据辅助的信道估计、协作式信道估计、半盲信道估计、盲信道估计。参考文献[7]采用基于数据辅助的信道估计算法,针对多小区大规模MIMO上行链路,当基站天线数无限大时,接收端解码得到的数据会受到不同用户数据之间的相关性产生类似于导频污染的交叉污染以及信道估计误差产生的自身污染。相比于导频信号,数据信号具有较低的交叉相关性,并且在信号帧中的数据部分通常要比导频部分更长。该文献利用此特性,有效地减少了交叉污染带来的影响。参考文献[8]提出了一种频率选择性稀疏信道估计算法,该算法主要利用相邻天线之间共享最小信息通过采用协作方式在接收端估计每条信道的脉冲响应,仿真结果表明提出的方法相比于最小均方误差(minimum mean square error,MMSE)具有良好的性能。参考文献[9]针对于传统的基于特征值分解(eigenvalue decomposition,EVD)和奇异值分解(singular value decomposition,SVD)半盲信道估计在实际计算过程中复杂度过高的缺陷,为此提出了一种基于快速单补偿近似幂迭代 (fast single compensation approximated power iteration,FSCAPI)子空间追踪算法,该算法收敛性快,具有很好的正交性,计算复杂度低。仿真结果表明,基于FSCAPI半盲信道估计能获得与基于EVD信道估计相近的性能。参考文献[10]针对大规模MIMO系统下行链路时分双工(time division duplexing,TDD)模式下,为了获得可靠的解码信息,信道增益必须保证是已知的。为此提出了一种可用于任何用户且不需要获取任何导频信息的盲信道估计算法,理论分析表明,在信道增益未知情况下系统性能远远优于信道增益已知的情况,仿真结果表明该算法在信噪比较大且导频信号未知的情况下具有很好的性能。
然而对于大规模MIMO系统来说,基站天线数目比较大,加剧了信道估计的复杂度。参考文献[11,12]分析了大规模MIMO系统运用MMSE及最小方差无偏(minimum variance unbiased,MVU)进行信道估计时均需要对方差矩阵进行求逆使得算法复杂度比较高的缺陷,提出了低复杂度贝叶斯信道估计和多项式扩展信道(polynomial expansion channel,PEACH)估计,仿真结果表明新提出的算法在计算复杂度大大降低的情况下能获得与其他算法相近的性能。参考文献[13]分析了大规模MIMO系统由于时延扩展长和基站天线数量多造成信道估计复杂度较高从而严重影响系统的性能。为此提出了一种低复杂度自适应稀疏滤波法,仿真结果表明该算法具有可行性并且相比较于传统的信道估计算法该算法能有效地提升系统的性能。参考文献[14]提出利用多项式扩展信道估计算法保证在低复杂度的条件下有效地提升信道估计的性能。
就大规模MIMO系统信道估计复杂度高的缺陷,在上行链路TDD模式下利用无线信道固有的稀疏特性[15],提出了一种基于快速傅里叶变换信道估计新算法,并与传统的最小二乘(least square,LS)、MMSE、DFT 进行了对比,仿真结果表明,该算法能在保持低复杂度的情况下,获得接近MMSE的性能。此外,该算法在多小区协同MIMO[16]和中继MIMO[17]系统中也能适用。
使用的符号定义如下:用斜体大小写字母表示矩阵和矢量。(A)-1、(A)T、(A)H分别表示矩阵的求逆、转置以及共轭转置,IN表示N阶单位阵。
2 系统模型
模型如图1所示,主要考虑单小区大规模MIMO-OFDM系统的TDD模式下的上行链路。该系统包括一个配备M根天线的基站和K个配备单天线的用户,N个子载波上每个用户发送 Np(0<Np<N)个导频序列用来对信道进行估计且发送的导频序列表示为 x=[x1,x2,…,xNp]T。因此在传送第 k个OFDM符号期间,基站接收的导频向量可以表示为:


图1 大规模MIMO系统模型
其中,A=diag(x)FNp,Lt表示N行N列的DFT矩阵的Np行Lt列的子矩阵;ni,k表示系统第k个用户与基站第 i根天线之间信道的高斯白噪声,其服从独立同分布,并且均值为0,方差为σ2;hi,k=[hi,k(1),hi,k(2),… ,hi,k(Lt),0,… ,0]T表示第k个用户与基站第i根天线最大时延长为Lt的信道脉冲响应。对于采样的抽头时延模型来说,信道包含的Lt个抽头可以表示为:
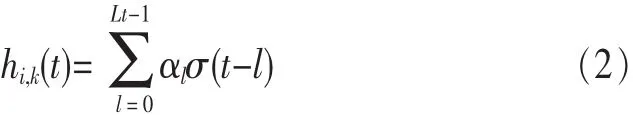
其中,αl表示均值为0的复高斯随机变量,并且满足E[αlαm*]=0,(l≠m)和 E[|αl|2]=σl2。由于无线信道具有稀疏特性,这就意味着在hi,k中的抽头数L要小于信道脉冲响应长度Lt,即式(2)中的一些抽头增益为零。
为了使分析简便,假设系统的所有子载波数为N全部用于传送导频序列,即N=Np,每条子载波循前缀的长度为Lcp,信号脉冲响应的长度Lt必须满足Lt<Lcp。
3 信道估计
先介绍传统的 DFT(discrete Fourier transform)信道估计算法的过程,接着阐述改进算法的过程。
3.1 DFT信道估计
对上述所建立的系统模型,用户到基站的每根天线之间的信道类似,单独针对用户到基站的单个信道进行阐述。在一个OFDM符号中,假设所有的子载波全部用于传送导频序列,因此采用LS估计的信道脉冲响应表示为:
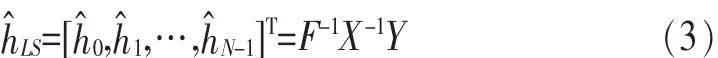
其中,F表示N×N的DFT矩阵;X表示的是已知的导频序列。信道脉冲响应的抽头数最多可以为Lcp,其他的抽头均看成是噪声。因此采用LS进行估计时只需要对h^LS前Lcp个抽头进行估计,即:

因此,时域上DFT信道估计可以表示为:
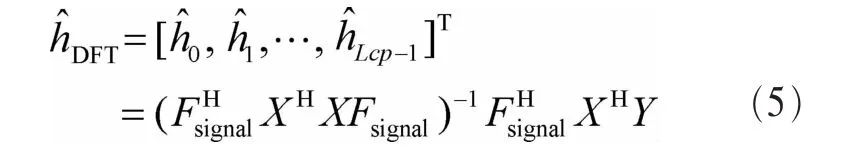
同理:

因此,时域上的噪声可以表示为:
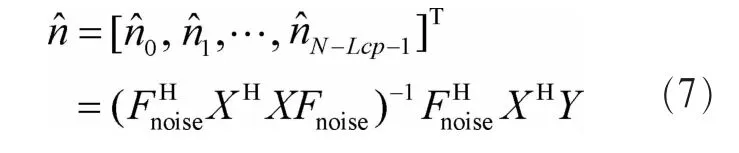
噪声的方差为:

3.2 改进的算法
本算法是在以上算法基础上进行改进的。算法过程如下。
输入 X,F,N
(1)计算出基站端天线接收到的信号R。
(2)采用LS对信道进行估计得到 hLS,对其进行升排列得到并记录对应的位置I。
(3)计算信道噪声的均值σn2。
(4)求出方差向量 ε。
(5)确认有效信道抽头的位置。
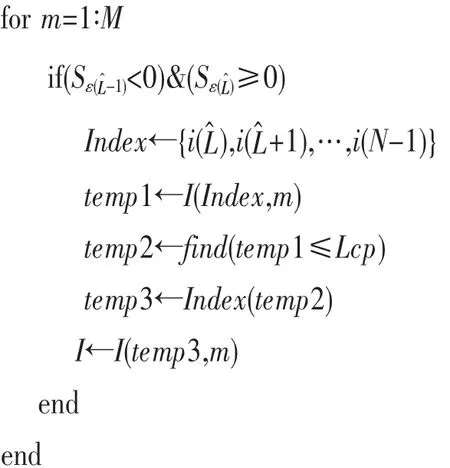
(6)运用上述更新的I,重组傅里叶变换矩阵Fpropose。
其主要思路如下。
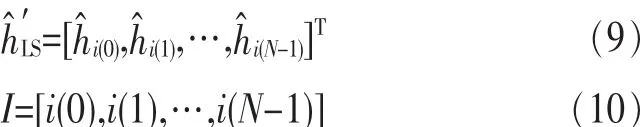
一般来说,无线信道有用信号抽头有较大的幅度值,幅度值越大,该位置的信道抽头发生的概率就越大。由此可以设定一个阈值对信道抽头进行选取,只要实际信道抽头个数L^被确定下来,信道抽头的位置也就确定下来。为此,假设有这样的一个方差向量:

其中:
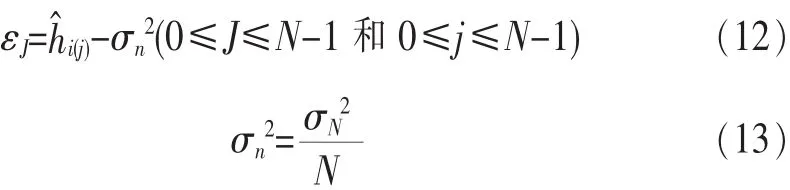
本文考虑的是理想情形,假设所估计的信道是理想信道,即信号的幅度值大于噪声的幅度值伴随着噪声,随着J的增大,εJ也随之不断增大。当J=N-L-1时,ε的前J项 Sε(J)和会趋近于零。
基于上述的考虑,可以通过确定的值来分离出信道抽头空间,即当 S<0且S≥0 时的位置就被确定了。当的位置被确定下来了,I中最后的项元素1),…,i(N-1)}就是信道抽头的位置。但在此基础上还必须确保其位置不得超过循环前缀的长度值,此时傅里叶变换矩阵可以表示为:

因此,时域上DFT信道估计可以表示为:

从式(10)和式(11)可以看出,可以发现提出的算法只需要计算稀疏信道抽头部分的方差,而传统的DFT需要计算前Lcp部分的方差,因此算法复杂度比传统的DFT信道估计算法更低。
4 计算复杂度分析
在大规模MIMO系统中,计算复杂度是衡量信道估计算法性能的一项重要指标。对第3节所给出的DFT信道估计、改进的信道估计及MMSE信道估计3种算法的计算复杂度进行分析与比较。一般来说,算法的计算复杂度可以定义为是该算法中的浮点运算(floating point operations,FLOPS)的次数[11]。为了使分析简便,本文将主要考虑该算法中复数的乘法运算,并将算法中复数乘法总的运算次数作为FLOPS的次数。
对一个维数为a的方阵来说,对其求逆需要2a次乘法运算;维数为a×b的矩阵与维数为b×c的矩阵相乘需要abc次乘法运算。据此基于DFT的信道估计算法和改进的信道估计算法在计算基站天线端接收到的信号时均需要N3+MN2次复数乘法运算。
在大规模MIMO系统中,由于信道相干时间是有限的,因此小区内基站只能同时服务一定数目的的用户量,并且用户在相干时间内也只能发送一定数目的数据样本[1]。现定义 ξ=M/K,仿真时载波数 N为 64,抽头数 L为 6,循环前缀Lcp为16,用户数K为4,3种算法的计算复杂度结果对比如图2所示。从图2中可以看出,随着ξ的增加,三者的计算复杂度越来越高,MMSE的计算复杂度递增梯度大于DFT和改进的算法,DFT和改进的算法计算复杂度递增梯度基本一致,这是由于改进的算法相比于DFT忽略了稀疏信道的噪声空间只是计算了信道的抽头部分。从图中还可以看出,ξ较小时,DFT和改进的算法计算复杂度多高于MMSE。当ξ增加到30时,MMSE计算复杂度开始高于改进的算法;当ξ增加到50时,MMSE计算复杂度开始高于DFT。由于大规模MIMO系统基站端天线数M较大,因此改进的算法计算复杂度会远远好于MMSE。
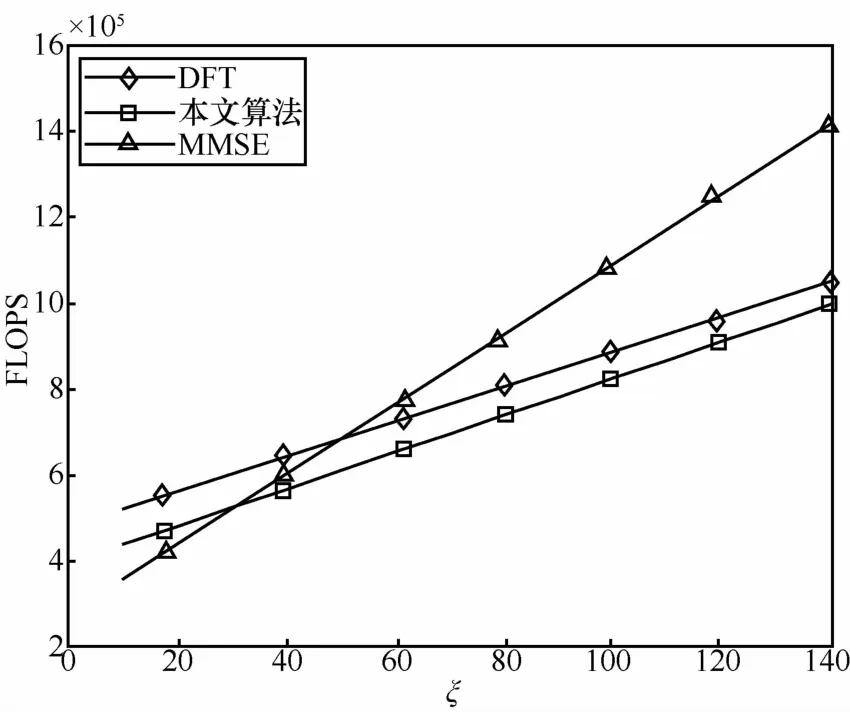
图2 不同ξ对应的浮点运算次数
5 仿真结果
通过蒙塔卡罗法对第3节中所提出的信道估计算法进行仿真。仿真过程中考虑的是单小区单用户系统,仿真性能采用归一化均方误差来衡量(NMSE),定义如下:
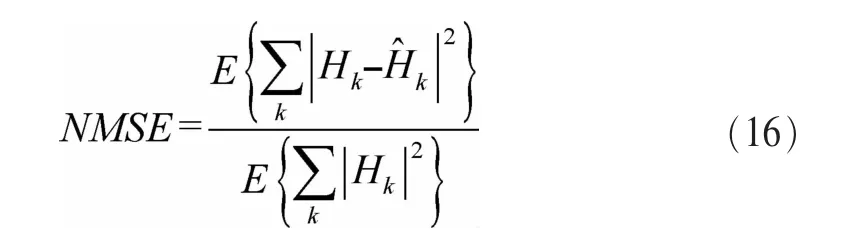
其中,Hk表示用户与基站某天线之间的信道频率响应的第k个子载波。算法仿真主要参数见表1。假设信道的时延功率谱为:

每条子信道的第一个抽头时延初始化为零,第一个抽头与最后一个抽头之间的其他抽头的位置随机产生。

表1 仿真参数
图3为信道脉冲响应长度一定时,不同信道抽头个数时的性能对比。仿真时信道脉冲响应长度设定为14,信道抽头个数设定为3和6两种情况。从图3(a)和图3(b)中可以看出,LS、DFT、MMSE、改进的算法4种信道估计算法中,改进的算法的性能明显优于其他3种算法。此外,信道脉响应长度一定时,改进的算法的性能随信道抽头数不同有差别,信道抽头数越少,性能越好,即信道稀疏度越小,性能越好,而信道稀疏度的大小对其他3种信道估计算法来说几乎没有影响。
图4为信道抽头个数一定时,不同信道脉冲响应长度时的性能对比。仿真时信道抽头个数设定为3,信道脉冲响应长度设定为8和14两种情况。从图4(a)和图4(b)中可以看出,改进的算法、传统的 DFT、MMSE、LS 4种信道估计方法中,改进的方法的性能很明显优于其他3种方法。此外,信道抽头个数一定时,LS、DFT、改进的算法的性能随信道脉冲响应长度的不同几乎没差异,MMSE存在差异,表现为信道脉冲响应长度越小,其性能越好。
图5为估计的信道抽头个数与实际的信道抽头个数的对比。仿真时信道脉冲响应长度设定为14,信噪比设定为20 dB。从图5中可以看出,估计出来的均值与实际上的值相差不大,信道抽头数较少时,两者差异较大。随着信道抽头个数的逐渐增加,两者的差异逐渐减小。当信道抽头个数为13时,两者相等。随着信道抽头个数的继续增加,两者的差异也逐渐增大。
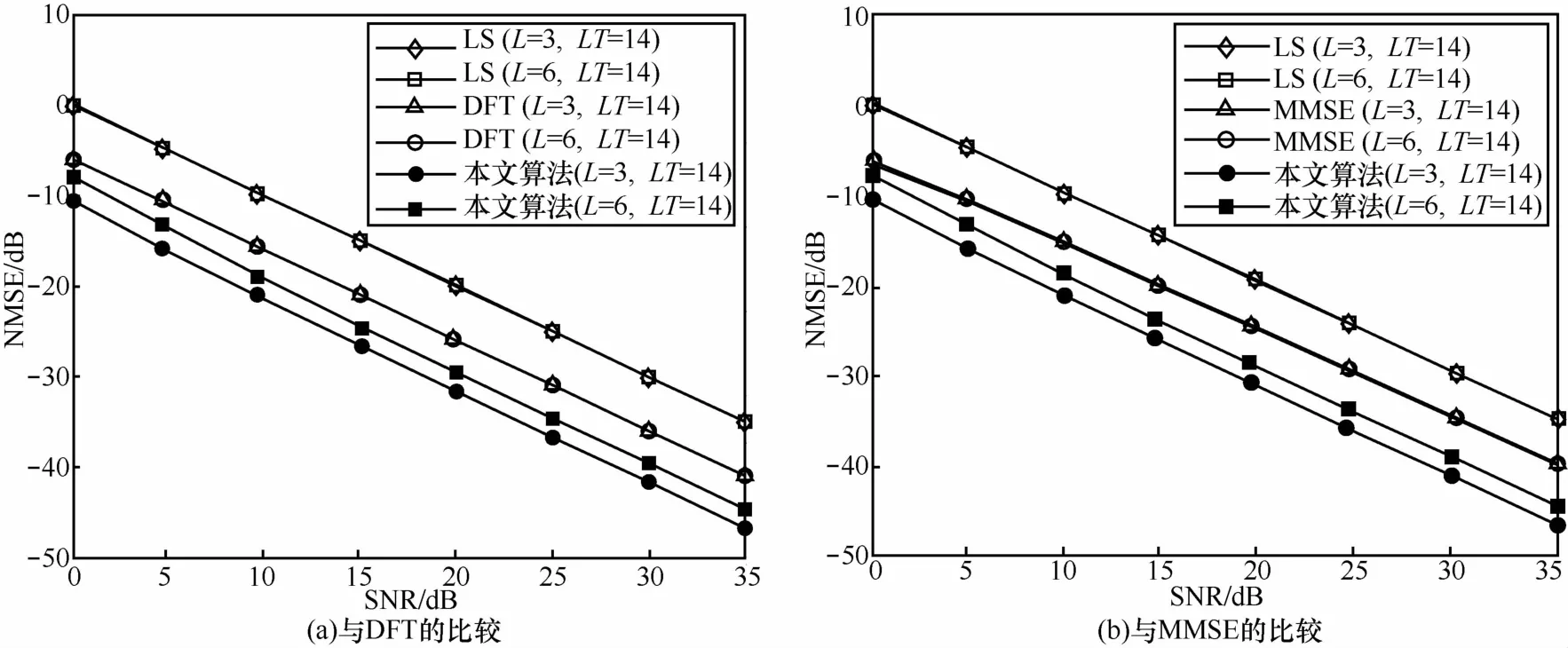
图3 抽头个数不同时信道估计的性能对比

图4 信道脉冲响应长度不同时信道估计性能的对比
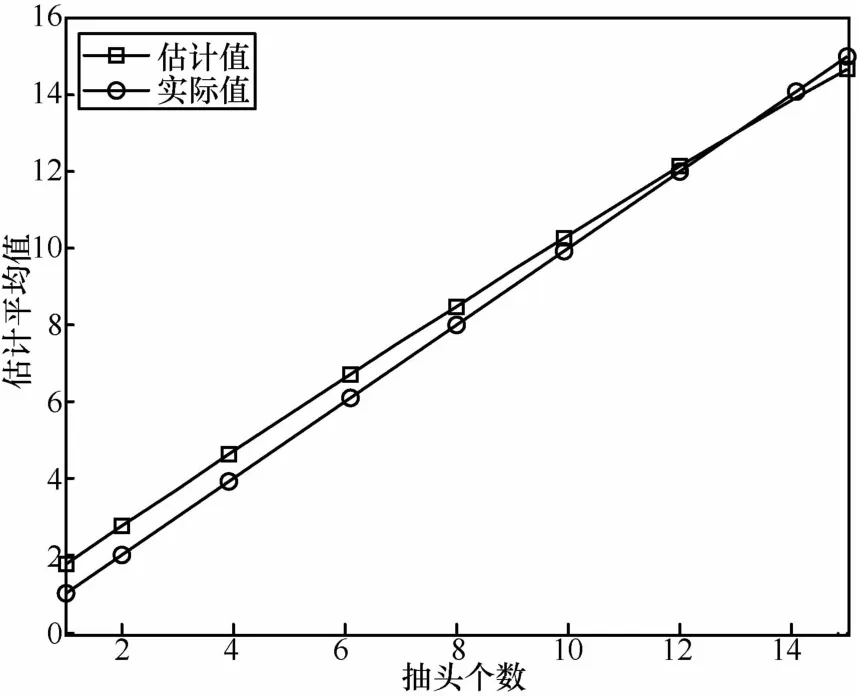
图5 估计的信道抽头个数与实际的信道抽头个数的对比
图6为不同算法对噪声敏感程度的关系。为了说明各种算法对噪声的敏感程度。假设噪声中叠加了均值为零的高斯白噪声w,即:

定义此噪声的信噪比为:

在进行仿真时信道脉冲响应长度设定为14,信道抽头个数设定为3,发送导频信噪比设定为20 dB。从图6中可以看出传统的LS对噪声影响的敏感程度最大,其次是MMSE和DFT,两者比较接近,但DFT稍优于MMSE,改进的算法对噪声的敏感度最小。综上可见,4种算法中改进算法的抗噪性能最优。

图6 不同算法对噪声敏感程度的影响
图7为各种算法的频谱效率对比。仿真时信道脉冲响应长度设定为14,信道抽头个数设定为3,信噪比设定为20 dB。从图7中可以看出,随着基站天线数目的增加,系统的频谱效率在不断提升,并且提升幅度越来越平缓,说明大规模MIMO系统可以通过增加基站天线数目来提升系统的频谱效率。改进的算法与其他算法相比,频谱效率几乎一致。
图7 各种算法的频谱效率对比
6 结束语
本文提出了一种低复杂度的大规模MIMO系统稀疏信道估计算法。其主要思想是将噪声空间与信道抽头空间分离开,对信道进行估计时,只需要计算信道抽头的部分,对于噪声部分可以忽略不计。这样大大减少了计算量,特别是对大规模MIMO系统来说效果更加明显。
[1]MARZETTA T L.Noncooperative cellular wireless with unlimited numbers of base station antennas [J].IEEE Transactions on Wireless Communications, 2010, 9 (11):3590-3600.
[2]JUNGNICKEL V,MANOLAKIS K,ZIRWAS W,et al.The role of small cells,coordinated multipoint,andmassive MIMO in 5G[J].IEEE Communications Magazine,2014,52(5):44-51.
[3]PANZNER B,ZIRWAS W,DIERKS S,et al.Deployment and implementation strategies for massive MIMOin 5G[C]/The 2014 IEEE Globecom Workshops (GC Wkshps),Dec 8-12,2014,Austin,TX,USA.New Jersey:IEEE Press,2014:346-351.
[4]BJOMSON E,HOYDIS J,KOUNTOURIS M,et al.Massive MIMO systems with non-ideal hardware:Energy efficiency,estimation, and capacity limits [J]. IEEE Transactions onInformation Theory,2014,60(11):7112-7139.
[5]LARSSON E,EDFORS O,TUFVESSON F,et al.Massive MIMO for next generation wireless systems [J].IEEE Communications Magazine,2014,52(2):186-195.
[6]FANG X,ZHANG Y F,CAO H Y,et al.Spectral and energy efficiency analysis with massive MIMO systems [C]/The 16th IEEE International Conference on Communication Technology,Oct 18-20,2015,Hangzhou,China.New Jersey:IEEE Press,2015:837-843.
[7] LI P.Data aided channel estimation in massive MIMO systems[C]//The 2014 International Workshop onHigh Mobility Wireless Communications (HMWC),Nov 1-3,Beijing,China.New Jersey:IEEE Press,2014:3.
[8]MASOOD M,AFITY L H,AL-NAFFOURI T Y.Efficient collaborative sparse channel estimation in massive MIMO [C]//The 2015 IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP),April 19-24,2015,South Brisbane,QLD,Australia.New Jersey:IEEE Press,2015:2924-2928.
[9]XU F Y,XIAO Y,WANG D.Adaptive semi-blind channel estimation for massive MIMO systems [C]/The2014 12th International Conference onSignal Processing (ICSP),Oct 19-23,2014,Hangzhou,China.New Jersey:IEEE Press,2014:1698-1702.
[10]NGO H Q,LARSSON E G.Blind estimation of effective downlink channel gains in massive MIMO[C]/The 2015 IEEE International Conference onAcoustics,Speech and Signal Processing (ICASSP),April 19-24,2015,South Brisbane,QLD,Australia.New Jersey:IEEE Press,2015:2919-2923.
[11]SHARIATIN, BJORNSON E, BENGTSSON M, etal.Low-complexity channel estimation in large-scale MIMO using polynomial expansion [C]/The 2013 IEEE 24th International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC),Spet 8-11,2013,London,England.New Jersey:IEEE Press,2013:1157-1162
[12]SHARIATIN, BJOMSON E, BENGTSSON M, etal.Low-complexity polynomial channel estimation in large-scale MIMO with arbitrary statistics [J].IEEE Journal of Selected Topics in Signal Processing,2014,8(5):815-830.
[13]GUI G,LIU N,XU L,et al.Low-complexity large-scale multiple-input multiple-output channel estimation using affine combination ofsparse leastmean square filters [J].IET Communications,2015,9(17):2168-2175.
[14]KOLOMVAKIS N,MATTHAIOU M,COLDREY M.Massive MIMO in sparse channels[C]/The 2014 IEEE 15th International Workshop on Signal ProcessingAdvances in Wireless Communications (SPAWC),June 22-25,2014,Toronto,ON,Canada.New Jersey:IEEE Press,2014:21-25.
[15]SHARIATIiN, BJOMSON E, BENGTSSON M, etal.Low-complexity polynomial channel estimation in large-scale MIMO with arbitrary statistics [J].IEEE Journal of Selected Topics in Signal Processing,2014,8(5):815-830.
[16]LI C G,ZHANG S L,LIU P,et al.Overhearing protocol design exploiting inter-cell interference in cooperative green networks [J].IEEE Transactions on Vehicular Technology,2016:441-446.
[17]LI C G,SUN F,CIOFFI J M,et al.Energy efficient MIMO relaytransimissionsviajointpowerallocations [J].IEEE Transactions on Circuits and Systems-II,2016:531-535.
Low-complexity sparse channel estimation for massive MIMO systems
FANG Xin,LIU Yunju,CAO Haiyan,PAN Peng
School of Communication Engineering,Hangzhou Dianzi University,Hangzhou 310018,China
Due to the high computational complexity of massive MIMO system,a low-complexity sparse channel estimation algorithm was proposed utilizing the inherent sparsity of the wireless communication channel to improve the estimation performance.The proposed algorithm separated channel tap from noise space based on the traditional discrete Fourier transform by adopting integral separation algorithm.This channel estimation algorithm need only calculate the channel tap,thus markedly reducing complexity of the algorithm.Numerical simulations show that proposed algorithm can approach to the performance of the minimum mean-square error estimator while maintaining lower complexity.
massive MIMO,channel estimation,sparsity,algorithm complexity
s:The National Natural Science Foundation of China for Youths (No.61501158),The Natural Science Foundation of Zhejiang Province (No.LY14F010019),Solid State Storage and Data Security Key Technology of Zhejiang Province (No.2013TD03)
TN911.22
A
10.11959/j.issn.1000-0801.2016149
2016-03-30;
2016-05-10
国家自然科学青年基金资助项目(No.61501158);浙江省自然科学基金资助项目(No.LY14F010019);浙江省固态存储和数据安全关键技术重点科技重新团队项目(No.2013TD03)

方昕(1975-),女,博士,杭州电子科技大学副教授、硕士生导师,主要研究方向为4G、5G移动通信系统物理层算法等。

刘云驹(1991-),男,杭州电子科技大学通信工程学院硕士生,主要研究方向为大规模MIMO系统。

曹海燕(1975-),女,博士,杭州电子科技大学副教授、硕士生导师,主要研究方向为宽带无线扩频通信理论、无线分集技术、OFDM多载波调制技术、信息论与编码技术以及MIMO与空时编码理论。

潘鹏(1983-),男,博士,杭州电子科技大学副教授、硕士生导师,主要研究方向为多用户检测技术、协作通信理论与技术和通信系统。
