基于拟合优度的频谱感知技术研究

2016-11-20卢光跃徐偲叶迎晖弥寅

电信科学 2016年5期

关键词：特征函数方差频谱

卢光跃，徐偲，叶迎晖，弥寅

（西安邮电大学无线网络安全技术国家工程实验室，陕西西安 710121）

研究与开发

基于拟合优度的频谱感知技术研究

卢光跃，徐偲，叶迎晖，弥寅

（西安邮电大学无线网络安全技术国家工程实验室，陕西西安 710121）

认知无线电技术实现了频谱资源的动态分配，提高了频谱资源的利用率。而准确高效的频谱感知是认知无线电的核心环节，因此研究快速高性能的频谱感知算法已经成为一个亟待解决的问题。近年来，拟合优度检验在频谱感知领域得到了广泛应用，实现了小采样点下的有效频谱感知技术。因此，基于拟合优度的频谱感知技术具有重要的研究意义。综述了GOF在频谱感知中的发展历程，介绍其基本原理、常见的拟合准则及拟合对象；然后在高斯信道下，对该类算法进行仿真对比；最后对GOF类算法的进一步研究进行了展望。

认知无线电；频谱感知；拟合优度检验；拟合准则；拟合对象

1 引言

频谱资源是一种非常重要的通信资源，有关政府部门已经对这种资源进行授权。美国FCC研究报告表明［1，2］，固定的频谱分配方式已导致所有可用频段利用效率低下，而且无线业务的不断增长导致可用频谱资源更加紧缺。

面对频谱危机，认知无线电［3，4］（cognitive radio，CR）应运而生，其核心思想是通过频谱感知（spectrum sensing，SS）技术发现“频谱空洞”，进而合理利用空闲频谱。可见，SS是 CR的前提和基础，次用户（secondary user，SU）必须实时监测频谱变化，并能够可靠地检测出“频谱空洞”，从而避免对主用户（primary user，PU）通信造成干扰。

目前，常见的SS算法有匹配滤波器检测、能量检测（energy detection，ED）算法、基于特征结构的感知算法和基于拟合优度（goodness of fit，GOF）检测的感知算法等。其中，匹配滤波器检测算法［5］在加性高斯白噪声环境下性能最优，但其对同步要求较高，且必须预知PU发射机信号的先验信息（如信号调制方式），限制了算法的应用范围；ED算法［6］不需要知道PU发射机信号的任何先验信息，易于实现，但易受噪声不确定度影响且不能精确估计噪声方差，导致ED算法存在门限设置困难以及顽健性低等缺点［7］；基于特征结构类算法［8-11］利用接收信号协方差矩阵特征值的性质进行感知，该算法检测性能优于ED算法且不受噪声不确定度的影响，但存在判决门限不够精确以及计算复杂度高等缺点。

众所周知，在认知无线电频谱感知中，检测性能、时效性、运算复杂度、是否需要先验信息以及是否受噪声不确定度的影响是衡量一个算法的关键因素。GOF类算法需要的数据量小、运算量低、性能优于ED算法并且能克服噪声不确定度的影响。因此，基于GOF的频谱感知算法具有重要的研究意义。

GOF类算法［12-14］的核心思想是基于接收信号的经验分布函数（empirical distribution function，EDF）构造统计量，将频谱感知转化为一种拟合优度检验问题。假设H0代表PU不存在，接收信号服从分布F0，H1代表PU信号存在，接收信号偏离F0。通过接收信号计算经验分布函数Fn，当H0成立时，Fn和F0应相当 “接近”，当H1成立时，Fn偏离F0。通常用两者间的距离来描述 “接近”的精确概念，Glivenko-Cantelli定理［15］定义了多种两个分布间的距离的精确概念，当然以不同的方式定义距离会得到不同的统计量。从上面的分析可知，GOF类算法是基于接收信号的整个概率分布，而不是基于某个特征参数，因此其检测性能应该优于能量检测，并且不需要任何授权用户信号的先验知识。

Wang等人最早将GOF算法用于频谱感知领域［14］，通过（Anderson&Darling，AD）检测准则度量接收信号的经验分布和特定正态分布之间的距离来判决授权用户是否使用频谱。随后，（Cramer-Von Mises，CM）［16］、（Kolmogorov-Smirnov，KS）［17］、（Order-Statistic，OS）［18］拟合准则也被用于度量这一距离。与传统的ED算法相比，此类算法检测性能更优，但是同样需要噪声方差的先验知识，属于半盲检测算法。在实际的频谱感知中，需要实时估计噪声方差，并且当估计值偏离实际值时，算法的性能受到了严重影响。

为了克服这一弱点，Lu等人［19-26］提出了几种不需要噪声方差信息的盲检测算法。Modified-GoF算法［24］对接收信号进行归一化处理，消除了噪声方差对GOF算法性能的影响。GOF-F算法［19］先对接收信号进行分段，求出每段数据均值方差之比，得到新的数据，理论上这些数据服从F分布，再使用AD准则拟合这些数据。类似地，参考文献［20，21］中改变了数据处理方法，得到服从学生t分布的数据，再进行拟合。这几种方法都是通过度量概率密度函数之间的距离来判断主用户是否存在，由于特征函数同样可以完整地描述接收信号的信息，因此参考文献［26］通过度量接收信号经验特征函数和特定特征函数之间的距离实现盲频谱感知。

前面介绍的GOF类频谱感知算法要求接收信号是静态缓慢变化的，这限制了接收信号必须是基带采样得到的，对于射频或者中频信号，前面的GOF类算法不再适用［27］。对此，Lu等人提出了适用于射频或者中频采样得到的动态信号的GOF类算法，该类算法计算了接收信号每个采样点能量，理论上能量值服从X2分布，再使用AD准则进行拟合［28，29］。参考文献［30］和参考文献［31］中将单边 AD 准则、似然比（like lihood rate，LLR）准则用于这一模型，提升了性能。随后，针对实际通信中存在的非高斯噪声，高斯混合噪声模型［32］以及米德尔顿噪音场景下［33］GOF类算法进行了进一步研究。

最近的研究中，GOF类算法在各种不同的频谱感知环境中得到了应用，参考文献［35］将GOF方法应用到多输入多输出（multiple input multiple output，MIMO）模型中，对接收数据的特征函数进行拟合，理论分析和仿真结果表明，在MIMO系统中，基于特征函数的频谱盲检测方法比基于能量检测的频谱检测方法和基于特征值的频谱盲检测方法具有更好的性能。参考文献［36］提出了一种噪声方差未知时，基于拟合优度的多天线协作频谱检测方法。通过计算多个天线采样样本均值和方差比的分布函数与经验分布函数之间的AD距离，并与备选的门限值比较，实现频谱检测。理论分析和仿真结果表明，基于AD检验的协作检测比基于随机矩阵的协作检测具有更好的性能，特别是在低信噪比和小样本条件下。参考文献［37］中先计算正交频分复用系统循环前缀和被复制数据间的相关系数，再利用GOF度量其经验分布与理论分布之间的距离，实现频谱检测。

现有的GOF类算法分类如图1所示，重点介绍了单节点的GOF类算法。

2 GOF类频谱感知算法一般步骤

通常，SS可以表述为一个二元假设检验问题，即存在两种假设：H0表示PU不存在，频谱空闲，SU可接入该频谱；H1表示PU存在，频谱被占用，SU不可接入该频谱。因此，SS的数学模型［13］可描述为：

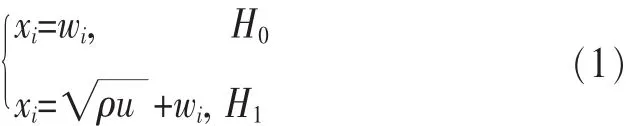
其中，xi是第 i时刻（i=1，2，…，L）的接收信号，wi是均值为0、方差为σ2的加性高斯白噪声，变量ρ满足SNR为信噪比，u是PU发送的信号。接收端xi可以是基带、中频或者射频进行采样得到的。在基带采样得到的信号是缓慢变化的，这里称之为静态信号，不失一般性，假设u=｛1，-1｝［14］，在中频或者射频采样得到的信号随时间动态变化，假设u是载波信号或者零均值的高斯信号［27］。

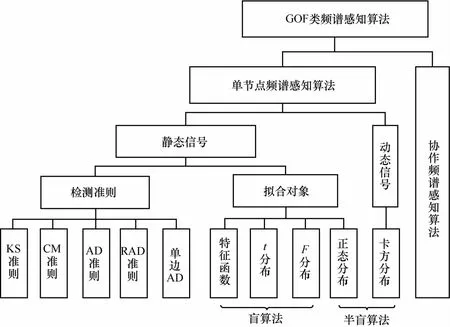
图1 GOF类频谱感知算法分类

在H0时，Y是独立同分布的序列，并且服从分布F0（y）。在 H1时，Y服从分布 F1（y）。假设数据y1≤y2≤…≤yL，样本经验分布函数定义如下：

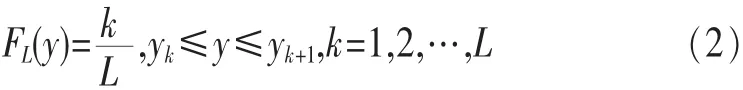
GOF是一种判断采样数据是否来自某一特定分布的数学方法。在H0假设下，由大数定律表明：当观测点数L→+∞，FL（y）依概率 1 收敛到 F0（y）［12］。因此通过 F0（y）和FL（y）之间的距离来判断H0假设是否成立。如果距离小于门限，判断H0成立，否则判断H1成立。

因此，GOF类频谱感知算法可描述如下：

步骤1 给定虚警概率α，选择拟合准则，根据拟合准则求判决门限t0；

步骤3 根据式（2）求Y的经验分布函数；

步骤4 依据不同的拟合准则求检验统计量；

步骤5 将检验统计量与门限对比，进行判决。

GOF类算法的关键点在于拟合准则的选择以及拟合对象的设计。接下来介绍几种常用的GOF拟合对象。

3 GOF拟合对象

针对在射频、中频或者基带采样得到接收信号的特点，需要采用不同GOF算法进行处理。下面分静态信号和动态信号两个场景来分析GOF类算法的拟合对象。

3.1 静态信号

对于基带采样得到的静态信号，从概率密度函数角度出发得到的拟合对象可以直接是服从正态分布的原始采样数据，或经处理后服从学生t分布以及F分布的拟合对象；也可以从特征函数角度设计拟合对象。不同的拟合对象得到的效果存在差异，在下文中会进一步说明。

3.1.1 拟合对象服从正态分布

那么在H0时，X是独立同分布的序列，并且服从分布，其中在 H1时，假设服从分布 F1（x）。

对观测数据直接拟合，拟合对象服从正态分布，运算复杂度低。但是当噪声方差未知时算法可靠性降低，因此可以对原始数据先进行处理，再进行拟合。

3.1.2 拟合对象服从学生t分布

当噪声方差已知时，目前有很多有效的检测算法，比如能量检测算法、AD检测算法［14］。然而当噪声方差未知时，这些算法性能会随方差估计的偏差增大而快速下降。基于学生t分布的GOF盲频谱感知算法［20］可以克服噪声不确定度的影响。

［19］可知，当授权用户不存在时，服从自由度为m-1的t分布，其累积分布函数函数记为 G0，m（y），即：

其中，Γ是伽玛函数。

3.1.3 拟合对象服从F分布

基于F分布的GOF盲频谱感知算法［21］也可以有效克服噪声不确定度的影响。与第3.1.2节对原始数据的处理方式相同：先将L个观测数据按先后顺序分成N个不同的部分，再根据式（6）求每段数据的样本均值和方差，最后将样本的均值平方与方差作比，得到新的序列：

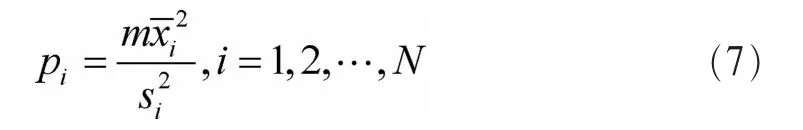
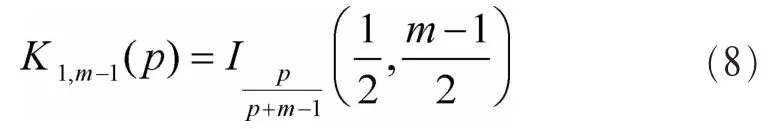
3.1.4 拟合对象是原始数据的特征函数

为了克服噪声不确定度，参考文献［26］中提出利用H0和H1时接收信号特征函数的差异进行频谱感知。在式（1）的频谱感知模型中，H0时xi是服从均值为0、方差为σ2的正态分布，其特征函数为 ∮0（υ）。H1时由于 PU 的存在，xi不服从均值为 0、方差为 σ2的正态分布，其特征函数偏离 ∮0（υ）。因此可以通过衡量接收数据的经验特征函数与H0时特征函数∮0（υ）之间的距离来判断主用户是否成立。参考文献［26］中将检验统计量设置为：

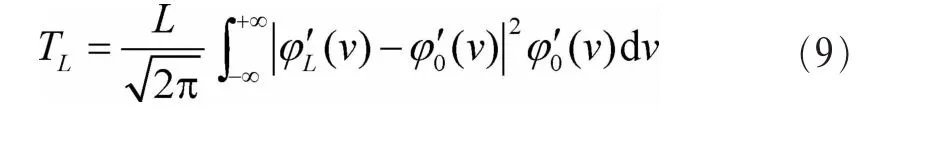
3.2 动态信号

在式（1）的频谱感知模型中，在中频或者射频端采样时，由于u不断变化，针对静态信号GOF类算法的性能会急剧下降，甚至差于ED算法的性能。

在动态信号模型下，可以使用基于卡方分布的GOF类频谱感知算法。该算法的模型如下：

其中，xi是第 i（i=1，2，…，L）时刻的接收信号，si是PU发送的信号第i（i=1，2，…，L）时刻在接收端的采样值，并且是一个时变的复信号，wi是均值为0、方差为σ2的加性高斯白噪声。

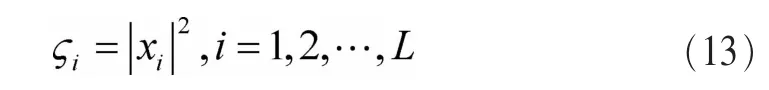
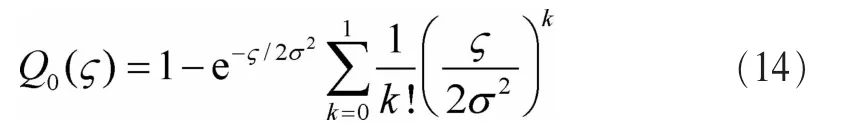
前文提出了多种对原始采样数据的处理方法，得到服从不同分布的新的数据作为拟合对象。针对静态信号，可以采用服从正态分布、学生t分布、F分布的拟合对象。当拟合对象服从正态分布时，算法复杂度较低，但是需要噪声方差信息，受噪声不确定度的影响。当拟合对象服从学生t分布、F分布以及拟合特征函数时，可以克服噪声不确定度的影响，并且性能较拟合对象服从正态分布时得到提升，但是增加了算法的复杂度。针对动态信号，介绍了新的模型，得到了服从卡方分布的数据。

对原始采样数据进行处理得到要拟合的数据，需要再选取合适的准则进行拟合，从而完成频谱感知。

4 GOF拟合准则

第2节中提到的GOF类算法是通过H0时Y的分布函数 F0（y）和 Y 的经验分布函数 FL（y）之间的距离，来判断H0假设是否成立。距离的取法多种多样，以不同的方式定义距离会得到不同的统计量。

GOF类算法的统计量基本上分为两类：上界型（极值型）和积分型。统一的形式如下：

上界型统计量：

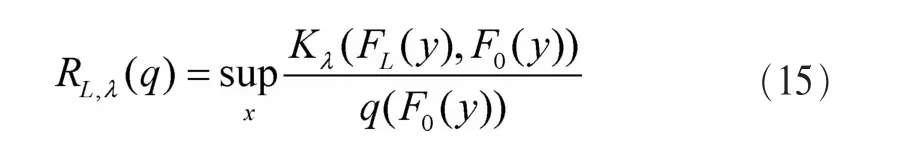
积分型统计量：

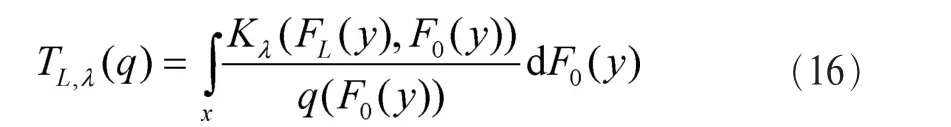
其中，q（t）为权函数。其一般形式为 q（t）=t2υ-1（1-t）2u-1。

取不同的参数λ和不同的权函数q（t），可以得到各种统计量。

|λ|越大，FL（y）与 F0（y）之间的细微差别会放得越大。从这个角度来说，选择|λ|较大的统计量更易区分这两个分布函数。但从另一个角度来看，当|λ|过大时，FL（y）与 F0（y）之间的细微差别被放大，使得研究检验统计量的样本分布变得比较困难。这从两方面可以得到体现：一是它的有限样本分布与极限分布偏差太大，做检验时由极限分布确定的临界值基本无用；二是数据的统计量值太大，也不利于计算机的计算或模拟，特别是靠近分布的两个端点（F0（y）接近于0或1的点）处的细微差别，在|λ|较大时被放得过大，很有可能造成数据的溢出而导致检验无法进行。另外，计算时间也是一个问题，计算时间过长会使所构造的检验基本无用。这就要求在这些问题中做出均衡选择。

选取最优的λ时，一般遵循如下两个准则：所构造的检验统计量在零假设成立时，能够较快地收敛到其对应的极限分布；统计量的值不会出现过分膨胀现象，从而导致计算过程无法进行或计算机本身引起的误差过大。

常用的GOF拟合准则有KS、CM和AD 3种。

4.1 KS检验

当 λ=1、q（t）=［t（1-t）］-1时，2RL，λ（q）就是 KS 统计量的平方。在KS检验［17］中，F0（y）和 FL（y）之间的距离定义如下：

其中：

其中，zi=F0（yi）。当 F0（y）和 FL（y）之间的距离 DL大于门限值时，认为 FL（y）已经偏离 F0（y），判断 H0成立。因此，通过P（DL＞t0|H0）=α 可以求出门限 t0，α 代表虚警概率。检测概率可以表示如下：

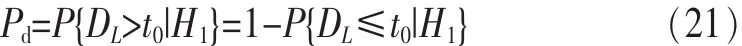
由参考文献［14］可知：当 L=14，α=0.05 时，t0=0.349；α=0.01 时，t0=0.148。当 L=28，α=0.05 时，t0=0.25；α=0.01 时，t0=0.3。当 L＞35，α=0.05 时，t0=1.36；α=0.01时，t0=，检测概率Pd收敛到1。在KS检验中，F0（y）和 FL（y）之间的距离用的是这两个函数之间的最大距离，这样运算量较小。但是由于没有使用分布函数所有位置的值来度量距离，因此与后两种使用分布函数所有信息的检验方法相比，性能较差。

4.2 CM检验

当 λ=1、q（t）=［t（1-t）］-1时，2TL，λ（q）就是CM的统计量。在 CM［16］检验中，F0（y）和 FL（y）之间的距离定义如下：

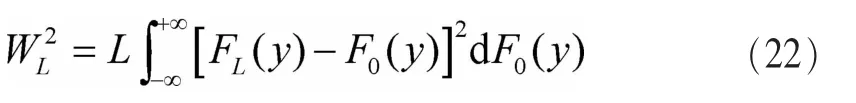
由参考文献［14］可知WL2可以被简化为下面的形式：

其中，zi=F0（yi）。由参考文献［14］可知：α=0.05 时，t0=0.462；α=0.01 时，t0=0.743。

检测概率可以表示如下：

L→+∞时，检测概率PCM以的速度收敛到1。其中，λ是大于零的任何数，。在CM检验中使用了分布函数所有位置的值来度量距离，与KS检验相比，虽然增加了运算量，但是检测性能得到了提升。对其加权函数进行改进，产生了AD检验，可以得到更优的性能。

4.3 AD检验

当 λ=1、q（t）=1 时，2TL，λ（q）就是AD统计量。在AD检验［14］中，F0（y）和 FL（y）之间的距离定义如下：

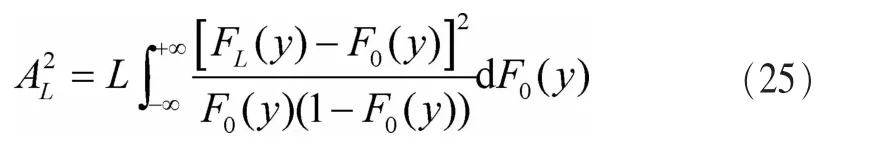
由参考文献［14］可知，AL2可以被简化为下面的形式：

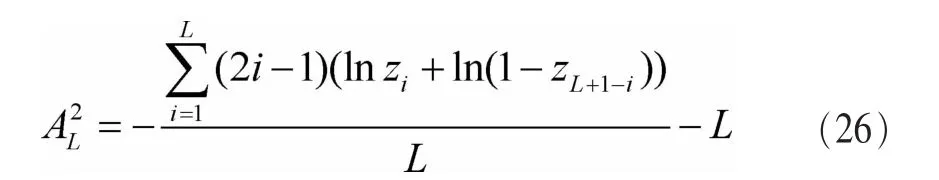
其中，zi=F0（yi）。通过 P（AL2＞t0|H0）=α 可以求出门限 t0。由参考文献［14］可知：当 L≥5，α=0.05 时，t0=2.492；α=0.01时，t0=3.857。

检测概率可以表示如下：

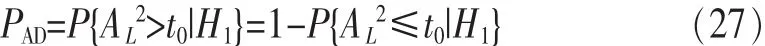
L→+∞时，检测概率PAD以的速度收敛到1。其中，λ是大于零的任何数。

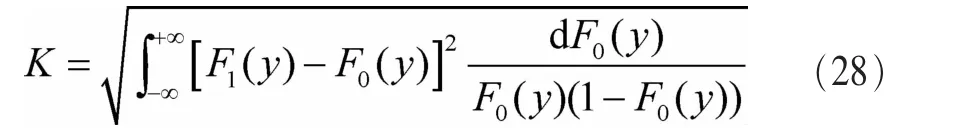
4.4 右尾AD检验

根据参考文献［38］可知，AD准则侧重双尾检验，而对于右尾分布更密集的数据，使用侧重右尾检验的RAD（right-tail AD）准则可以获得更理想的性能。当 λ=1、q（t）=t-1时，2TL，λ（q）就是 RAD 的统计量。在RAD检验［38］中，F0（y）和FL（y）之间的距离定义如下：

RL2可以被简化为下面的形式：

其中，zi=F0（yi）。通过 P（RL2＞t0|H0）=α 可以确定判决门限t0和虚警概率α的关系。

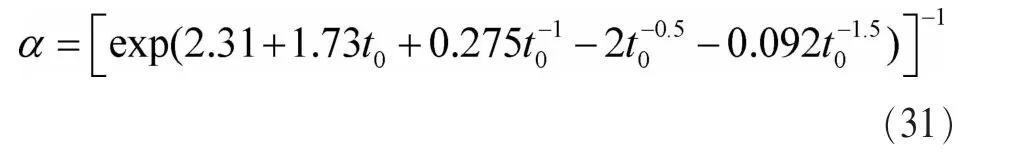
4.5 单边AD检验

AD 检验拟合分布对于 FL（y）＞F0（y）和 FL（y）＜F0（y）两种情况都适用。但在式（12）拟合对象服从卡方分布的模型中，H1时的拟合对象恒大于 H0时，也就是 FL（y）＜F0（y）恒成立。这时采用单边AD检验可以提升性能、降低计算复杂度。在单边 AD 检验［30］中，F0（y）和 FL（y）之间的距离定义如下：

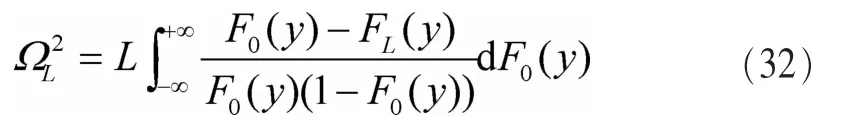
ΩL2可以被简化为下面的形式：

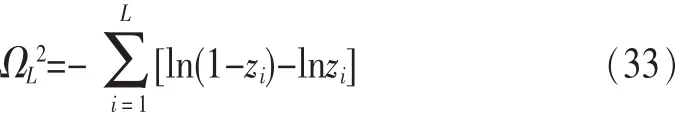
其中，zi=F0（yi）。

GOF类算法常用的拟合准则有KS、CM、AD、RAD以及单边AD。KS运算复杂度最低，性能最差。CM与AD复杂度相近，AD的性能略优于CM，RAD更侧重右尾密集的数据，单边AD在H1时的拟合对象恒大于H0时的情况下可以得到更好的性能。可以根据实际需求选择对应的拟合准则。

5 仿真分析

对文中的几种GOF算法以及ED算法进行10 000次Monte-Carlo模拟仿真实验，并通过考察一定Pf条件下算法所能达到的检测概率Pd来评价其性能。当存在噪声不确定度 B［8］时，真实的噪声方差在区间［σ2，ασ2］取值，其中，α=100.1B。如无特殊说明，仿真时L=28，Pf=0.05，σ2=1。因为ED算法需要知道噪声方差，因此在仿真中假设噪声方差σ2为1。

图2是ED算法与GOF类算法的性能对比。从图2可以看出，传统的ED算法在低信噪比时性能较差。当SNR=-2 dB时，AD可以达到0.99的检测概率，CM可以达到0.98的检测概率，KS可以达到0.95的检测概率，而ED算法的检测概率只有0.63。要使检测概率达到0.9，AD和CM要求信噪比达到-4 dB，KS要求信噪比达到-3 dB，而ED算法需要的信噪比达到0 dB。AD和CM的性能比ED好了约4 dB，KS比ED好了约3 dB。

ED算法与GOF类算法的判决门限和采样点数的关系如图3所示。由图3可见，ED算法的门限值随着采样点数的增加而增加，GOF类算法的门限值随着采样点数的增加不发生变化，由此可见，GOF类算法的门限不受采样点数的影响。

图4、图5分别是ED算法、AD拟合正态分布算法、AD拟合学生t分布算法在B=0、B=2时的性能比较。由图4可知，当B=0时，AD拟合学生t分布算法略优于AD拟合正态分布算法，而这两种GOF类算法明显优于ED检测算法。由图5可知，当B=2时，对比图4、图5可知，采用 AD拟合学生 t分布算法得到的 Pd、Pf和 B=0时得到的 Pd、Pf相等，而采用ED算法、AD拟合正态分布算法得到的Pd、Pf发生了变化。比如在SNR=-4 dB时，采用ED算法的Pd分别从0.38变为0.49，采用ED算法、AD拟合正态分布算法的 Pf分别从 0.05变为 0.18、0.05变为 0.09，显然，此时 Pf未达到预设的要求（即Pf=0.05）。由此可见，ED算法、AD拟合正态分布算法受噪声不确定度影响，而AD拟合学生t分布算法可以克服噪声不确定度的影响。

图2 ED与GOF类算法性能比较

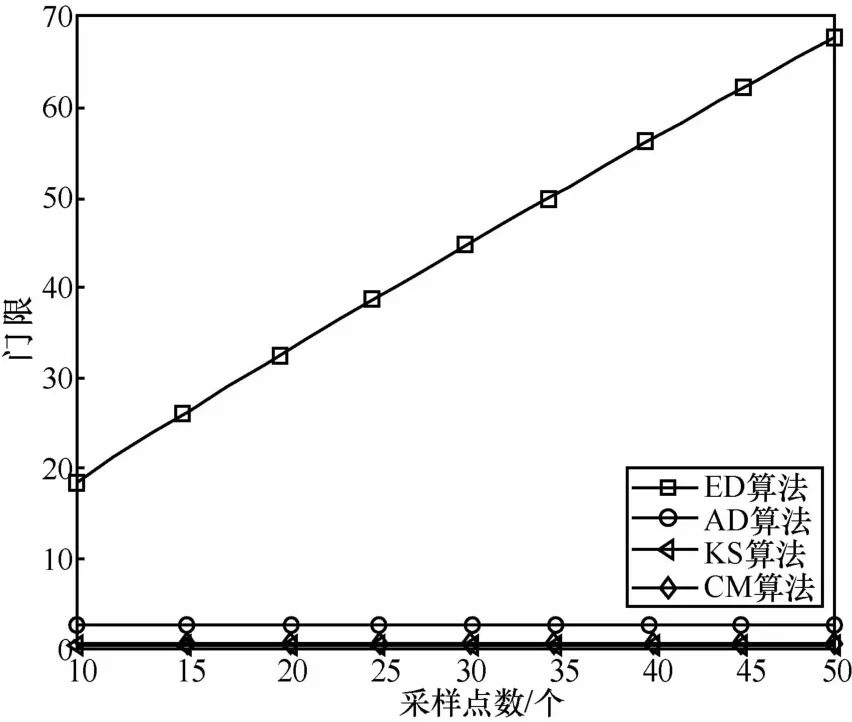
图3 ED与GOF类门限和采样点数的关系

图6是AD拟合学生t分布、拟合特征函数这两种盲频谱感知算法性能比较。从图6可见，噪声不确定度分别为0、2时，AD拟合学生t分布算法、拟合特征函数算法得到的Pd、Pf几乎不变，这说明了这两种算法均不受噪声不确定度的影响。而AD拟合学生t分布算法优于拟合特征函数算法，比如SNR=-4 dB时，AD拟合学生t分布算法的检测概率为0.91，而拟合特征函数算法的检测概率为0.83。

图4 B=0时ED与GOF类算法拟合性能对比

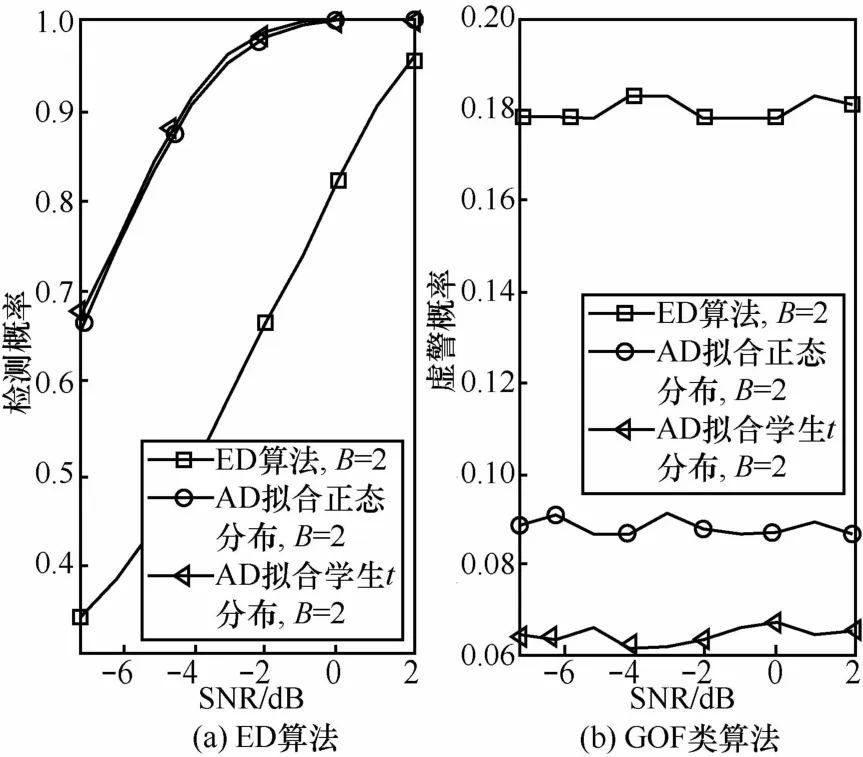
图5 B=2时ED与GOF类算法拟合性能对比

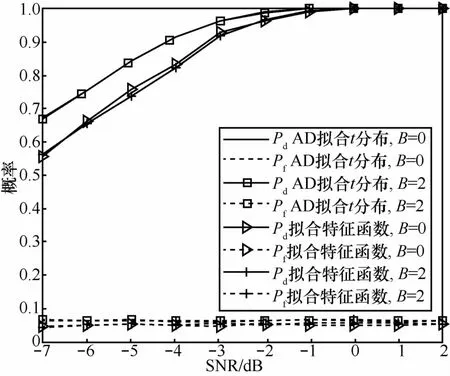
图6 有无噪声不确定度时GOF类算法性能对比

为进一步比较GOF类算法的性能，图7给出了SNR=-4 dB，B=0时多种算法的ROC性能特征曲线。从图7可见，GOF类算法的性能明显优于ED算法，这进一步验证GOF类算法具有更高的可靠性。

图7 GOF类算法的ROC性能特征曲线

6 结束语

GOF类算法在低信噪比的情况可以实现快速有效的盲频谱感知，选择合适的拟合对象还可以克服噪声不确定度的影响。因此，基于GOF的频谱感知技术具有重要的研究价值。本文介绍了GOF类算法的基本原理、常用的拟合准则以及拟合对象，并对GOF类算法在频谱感知领域的研究现状进行了研究。从最后各种GOF类算法的仿真结果可见，相较于传统的ED算法，GOF类算法有更优越的检测性能，实现盲感知并且能够克服噪声不确定度的影响。从目前研究的成果来看，如何将GOF理论应用到协作频谱感知中以及如何在中频、射频信号中使用GOF理论还有待进一步的研究。

参考文献：

［1］ KOLODZY P.Spectrum policy task force report ［J］.Federal Communications Commission Technology，2002，40（4）：147-158.

［2］ISLAM M H，KOH C L，OH S W，et al.Spectrum survey in Singapore：occupancy measurements and analysis ［C］／The 3rd International Conference on Cognitive Radio Oriented Wireless Networks and Communications （CROWNCOM’08），May 15-17，2008，Singapore.New Jersey：IEEE Press，2008：1-7.

［3］SIMON H. Cognitive radio： brain-empowered wireless communications ［J］.IEEE Journalon Selected Areasin Communications，2005，23（2）：201-220.

［4］MITOLA J，MAGUIRE G.Cognitive radio：making software radios more personal ［J］.IEEE Personal Communications，1999，6（4）：13-18.

［5］CABRIC D，MISHRA S M，BRADERSEN R W.Implementation issues in spectrum sensing for cognitive radios ［C］／／The 38th Asilomar Conference on Signals System and Computers，November 7-10，2004，Monterey，Mexico.New Jersey：IEEE Press，2004：772-776.

［6］DIGHAM F F，ALOUINI M S，SIMON M K.On the energy detection of unknown signals over fading channels ［J］.IEEE Transactions on Communications，2007，55（1）：21-24.

［7］TANDRA R，SAHAI A.SNR walls for signal detection［J］.IEEE Journal of Selected Topics in Signal Processing，2008，2（1）： 4-17.

［8］王颖喜，卢光跃.基于最大最小特征值之差的频谱感知技术研究［J］.电子与信息学报，2010，32（11）：2572-2574.WANG Y X，LU G Y.DMM based spectrum sensing method forcognitive radio systems ［J］.JournalofElectronics&Information Technology，2010，32（11）：2572-2574.

［9］ZENG Y H，LIANG Y，Maximum-minimum eigenvalue detection for cognitive radio ［C］／The 18th Annual IEEE International Symposium on Personal，Indoor and Mobile Radio Communications （PIMRC’07），September 3-7，2007，Greece，Athens.New Jersey：IEEE Press，2007：1-5.

［10］卢光跃，弥寅，包志强，等.基于特征结构的频谱感知算法［J］.西安邮电大学学报，2014，19（2）：1-12.LU G Y，MI Y，BAO Z Q，et al.Cooperative spectrum sensing algorithms based on eigenvalue structure of the received signal［J］.Journal of Xi’an University of Posts and Telecommunications，2014，19（2）：1-12.

［11］弥寅，卢光跃.基于特征值极限分布的合作频谱感知算法［J］.通信学报，2015，36（1）：1-6.MI Y，LU G Y.Cooperative spectrum sensing algorithms based on limiting eigenvalue distribution［J］.Jounal of Communication，2015，36（1）：1-6.

［12］STEPHENS M A.EDF statistics for goodness of fit and some comparisons ［J］.Journal of the American Statistical Association，1974，69（347）：730-737.

［13］ANDERSON T W，DARLING D A.A test of goodness of fit［J］.Journal of the American Statistical Association，1954，49（268）：765-769.

［14］WANG H，YANG E H，ZHAO Z，et al.Spectrum sensing in cognitive radio using goodness offittesting ［J］.IEEE Transactions on Wireless Communications， 2009， 8 （11）：5427-5430.

［15］SHARIPOV O S.Glivenko-Cantellitheorems ［M］.Berlin：Springer，2011：612-614.

［16］LEI S，WANG H，SHEN L.Spectrum sensing based on goodness of fit tests［C］／International Conference on Electronics，Communications and Control （ICECC），September 9-11，2011，Ningbo，China.New Jersey：IEEE Press，2011：485-489.

［17］ZHANG G，WANG X，LIANG Y C，et al.Fast and robust spectrum sensing via Kolmogorov-Smirnov test ［J］.IEEE Transactions on Communications，2010，58（12）：3410-3416.

［18］ROSTAMI S，ARSHAD K，MOESSNER K.Order-statistic based spectrum sensing for cognitive radio ［J］.IEEE Communications Letters，2012，16（5）：592-595.

［19］叶迎晖，卢光跃，弥寅.利用样本特征的盲频谱感知算法［J］.信号处理，2015.YE Y H，LU G Y，MI Y.Blind spectrum perception algorithm using the sample characteristics ［J］.Signal Processing，2015.

［20］SHEN L，WANG H Q，ZHANG W，et al.Blind spectrum sensing for cognitive radio channels with noise uncertainty ［J］.IEEE Transactions on Wireless Communications，2011，10 （6）：1721-1724.

［21］YE Y H，LU G Y.Blind spectrum sensing based on the ratio of mean square to variance ［J］.Journal of China Universities of Posts&Telecommunications，2016，23（1）：42-48.

［22］苏杭，叶迎晖，卢光跃.基于二项分布的快速盲频谱感知算法［J］.电视技术，2016，40（4）：96-100.SU H，YE Y H，LU G Y.Fast blind spectrum perception algorithm based on the binomial distribution ［J］.Journal of TV Technology，2016，40（4）：96-100.

［23］PATEL D K，TRIVEDI Y N.Non-parametric blind spectrum sensing based on censored observations for cognitive radio［J］.Journal of Signal Processing Systems，2015，78（3）：275-281.

［24］卢光跃，叶迎晖，孙宇等.克服噪声不确定度的拟合优度检验频谱感知算法［J］.电讯技术，2016，56（1）：24-29.LU G Y，YE Y H，SUN Y，et al.Spectrum sensing method based on goodness of fit test under noise uncertainty ［J］.Telecommunication Technology，2016，56（1）：24-29.

［25］YE Y H，LU G Y.Blind spectrum perception algorithm using student distribution ［C］／The 10th National Radio Application and Management of Academic Conferences，December 6，2015，Nanjing， China. Beijing： People’s Posts and Telecommunications Press，2015：80-84.

［26］沈雷，王海泉，赵知劲，等.认知无线电中基于拟合优度的频谱盲检测算法研究［J］.通信学报，2011，32（11）：27-34.SHEN L，WANG H Q，ZHAO Z J，et al.Blind spectrum sensing based on goodness of fit test for cognitive radio in noise of uncertain power［J］.Journal of Communication，2011，32（11）：27-34.

［27］NGUYEN-THANH N，KIEU-XUAN T，KOO I.Comments on“spectrum sensing in cognitive radio using goodness of fit testing” ［J］.IEEE Transactions on Wireless Communications，2012，11（10）：3409-3411.

［28］TEGUIG D，SCHEERS B.Spectrum sensing method based on goodness of fit test using chi-square distribution ［J］.Electronics Letters，2014，50（9）：713-715.

［29］王海泉，雷绍婷，沈雷.快衰落信道下修正的卡方-AD联合检测［J］.电路与系统学报，2013，18（1）：28-32.WANG H Q，LEI S T，SHEN L.Modified chi-square-AD joint detection on fast fading channels ［J］.Advances in New and Renewable Enengy，2013，18（1）：28-32.

［30］JIN M，GUO Q，XI J，YU Y.Spectrum sensing based on goodness of fit test with unilateral alternative hypothesis ［J］.Electronics Letters，2014，50（22）：1645-1646.

［31］TEGUIG D.Spectrum sensing method based on the likelihood ratio goodness of fit test［J］.Electronics Letters，2015，3（9）：488-494.

［32］TEGUIG D，SCHEERS B，NIR V L，et al.Spectrum sensing method based on the likelihood ratio goodness of fit test under noise uncertainty［J］.Esrsa Publications，2014，3（3）：488-494.

［33］PATEL D K， TRIVEDI Y N. Goodness-of-fit-based non-parametric spectrum sensing under Middleton noise for cognitive radio［J］.Electronics Letters，2015，51（5）：419-421.

［34］叶迎晖，卢光跃.基于相关系数的多天线协作盲检测算法［J］.电视技术，2016，40（4）：65-68.YE Y H，LU G Y.Multiple antenna collaboration blind detection algorithm based on correlation coefficient［J］.Journal of TV Technology，2016，40（4）：65-68.

［35］沈雷，陈佩，王海泉，等.多输入多输出系统基于特征函数频谱盲检测［J］.电波科学学报，2013，28（6）：1110-1115.SHEN L，CHEN P，WANG H Q，et al.Bind spectrum sensing in MIMO cognitive radio channels ［J］.Chinese Journal of Radio Science，2013，28（6）：1110-1115.

［36］沈雷，王海泉，赵知劲.认知无线电中基于拟合优度的多天线协作频谱检测［J］.电路与系统学报，2010，15（5）：79-84.SHEN L，WANG H Q，ZHAO Z J.Cooperative spectrum sensing based on goodness of fit in multi-antenna cognitive radio ［J］.Journal of Circuits and Systems，2010，15（5）：79-84.

［37］王海泉，潘伟丽，沈雷.正交频分复用系统的拟合优度检测算法［J］.电波科学学报，2013，28（1）：142-146.WANG H Q，PAN W L，SHEN L.A spectrum sensing method based on goodness of fit testing for OFDM systems［J］.Chinese Journal of Radio Science，2013，28（1）：142-146.

［38］SINCLAIR C D，SPURR B D，AHMAD M I.Modified anderson darling test ［J］.Communication in Statistics-Theory and Methods，1990，19（10）：3677-3686.

Research on spectrum sensing technologies based on goodness of fit

LU Guangyue，XU Cai，YE Yinghui，MI Yin
National Engineering Laboratory for Wireless Security，Xi’an University of Posts and Telecommunications，Xi’an 710121，China

Cognitive radio technology has achieved the dynamic allocation of spectrum resources，and improves the utilization rate of spectrum resources.Accurate and efficient spectrum sensing is the key step in cognitive radio.Developing a fast and high-performance spectrum sensing method has become an urgent problem to be solved.In recent years，goodness of fit（GOF）theory has been applied widely in the field of spectrum sensing and the effective spectrum sensing technology under small sample point has been implemented.Therefore，the research on spectrum sensing technology based on GOF has very significant value.The development process of GOF in areas of cognitive radio spectrum sensing was summarized，its basic principle common fitting criterion and fitting object were introduced.The simulation comparison of the algorithm was carried under the Gaussian channel and its prospects of further research was forecasted finally.

cognitive radio，spectrum sensing，goodness of fittest，fitting criterion，fitting object

TN92

10.11959／j.issn.1000-0801.2016136

2016-02-26；

2016-04-29